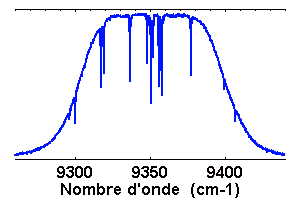
Spectre de Procyon dans le proche infrarouge, aux alentours de
obtenu avec le FTS (Fourier Transform Spectrometer) du télescope CFH.
Crédit :
ASM
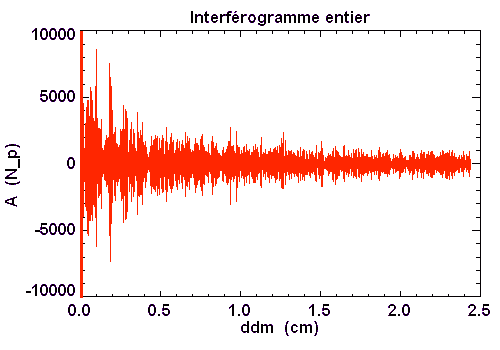
Des motifs d'interférence se retrouvent à diverses différences de marche. A grande différence de marche, l'interférogramme est dominé par le bruit de photons.
Crédit :
ASM
Filtre
Un filtre est nécessaire pour sélectionner une bande passante limitée du spectre étudié. L'interférogramme associé à cet exemple va comprendre des motifs liés au signal spectral dans le filtre.
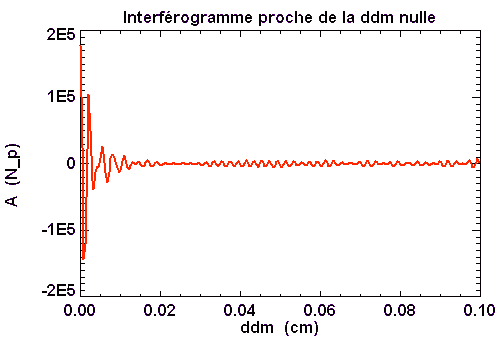
Le contraste du signal chute rapidement dès lors que la différence de marche n'est plus nulle.
Crédit :
ASM
Interférogramme proche de la différence de marche nulle
Au proche voisinage de la différence de marche nulle, les franges restent bien contrastées. Le contraste des franges baisse rapidement au fur et à mesure de l'éloignement de la différence de marche nulle.
Interférogramme complet
L'interférogramme complet comprend divers motifs, construits selon les interférences entre les raies sélectionnées par le filtre.
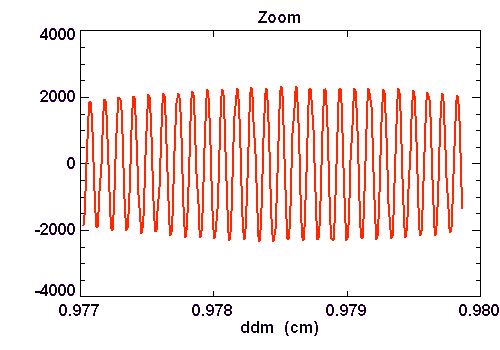
Zoom sur un motif de l'interférogramme.
Crédit :
ASM
Zoom dans l'interférogramme
La visualisation d'un train de franges de l'interférogramme montre une belle portion de sinusoïde modulée par l'enveloppe du train de franges.
 Objectifs
Objectifs
Décrire l'allure de l'interférogramme.
Le spectre théorique initial
Le spectre comprend les données en entrée :
- L'intensité spectrale
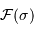 .
. - L'unité
spectrale employée est le nombre d'onde,
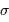 , exprimé en
, exprimé en
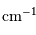 .
.
L'avantage de travailler avec une telle unité spectrale est d'avoir des
variables directement conjuguées entre le spectre et l'interférogramme :
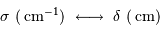
Ces unités employées, quoique hors SI, présentent l'avantage d'être inverses l'une de l'autre.
Interférogramme et TF
L'interférogramme calculé représente la quantité :
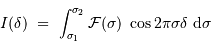
où l'on reconnaît la partie réelle de la TF de la densité
spectrale 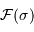 .
.
L'interférogramme réalise physiquement la TF de la distribution spectrale de la source.
La TF inverse de l'interférogramme, calculée, permet de remonter au spectre.
Etendue de faisceau
L'interféromètre étant réglé en anneaux, le principe instrumental ne nécessite pas l'introduction d'une fente d'entrée, contrairement à un spectromètre à réseau.
L'étendue de faisceau n'est donc pas drastiquement limitée par une fente ;
en pratique, elle est limitée par la nécessité de travailler dans un coeur de frange.
Ceci est convenablement dimensionné dans un exercice.
Le signal sur l'axe
L'animation ci-jointe montre comme évolue l'interférogramme en fonction de la différence de marche, pour une onde strictement monochromatique.
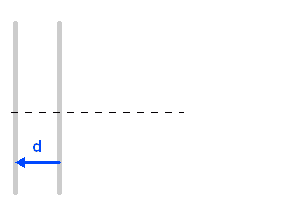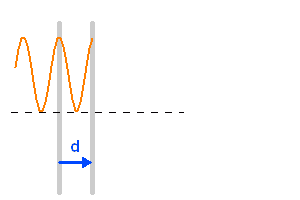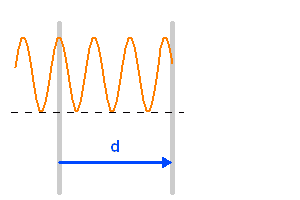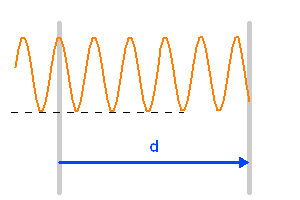
En ramenant optiquement les 2 miroirs sur l'axe, on peut représenter directement la différence de marche, et en déduire le signal oscillant pour une source monochromatique.
Crédit :
ASM
Les anneaux
Les miroirs étant parallèles, les franges d'interférence présentent la symétrie de révolution autour de l'axe optique ; ce sont des
anneaux. On remarque que, par stationnarité de la différence de marche 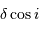 , avec
, avec  l'inclinaison, autour de l'inclinaison nulle, la tache centrale est relativement plus large que les autres anneaux.
l'inclinaison, autour de l'inclinaison nulle, la tache centrale est relativement plus large que les autres anneaux.
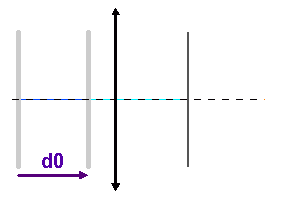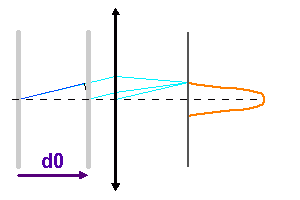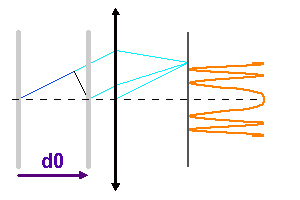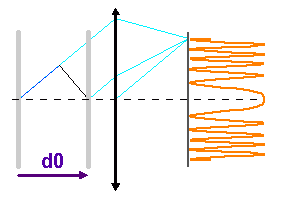
Construction des anneaux d'interférence, pour des inclinaisons importantes sur l'axe.
Crédit :
ASM
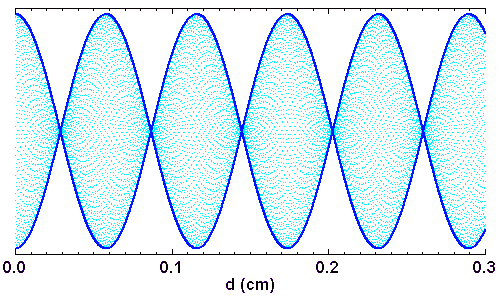
 Interférogramme d'un doublet
Interférogramme d'un doublet
Difficulté : ☆☆
Temps : 30 min
On illumine un interféromètre de Fourier avec une source ponctuelle présentant un doublet, aux nombres d'onde 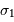 et
et 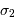 voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
Question 1)
Déterminer l'expression de l'interférogramme 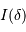 . Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
. Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
Les 2 ondes peuvent-elles être cohérentes ?
On rappelle :
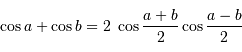
Question 2)
Déterminer la période des battements et représenter l'allure de l'interférogramme, pour le doublet du sodium :
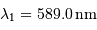 et
et 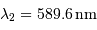 .
.
 Influence de l'inclinaison
Influence de l'inclinaison
Difficulté : ☆☆
Temps : 30 min
Les 2 miroirs d'un interféromètre de type Michelson sont réglés parallèles (au rôle de la séparatrice près).
On note 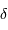 la différence de marche à incidence nulle.
la différence de marche à incidence nulle.
Question 1)
Montrer que la différence de marche pour un faisceau d'incidence  devient
devient
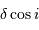 . Faire un schéma.
. Faire un schéma.
[1 points]
Question 2)
A quelle condition la différence de marche varie-t-elle de moins d'une fraction 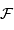 de longueur de longueur d'onde ?
de longueur de longueur d'onde ?
[1 points]
Question 3)
Faire l'application numérique pour une ddm de 1 cm, et une fraction limitée à 10%, à 1 micron.
[1 points]

 obtenu avec le FTS (Fourier Transform Spectrometer) du télescope CFH.
obtenu avec le FTS (Fourier Transform Spectrometer) du télescope CFH.



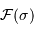 .
.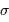 , exprimé en
, exprimé en
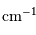 .
.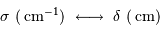
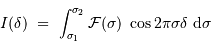
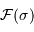 .
.

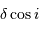 , avec
, avec  l'inclinaison, autour de l'inclinaison nulle, la tache centrale est relativement plus large que les autres anneaux.
l'inclinaison, autour de l'inclinaison nulle, la tache centrale est relativement plus large que les autres anneaux.

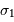 et
et 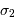 voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
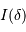 . Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
. Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
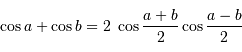
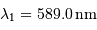 et
et 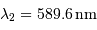 .
.
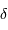 la différence de marche à incidence nulle.
la différence de marche à incidence nulle.
 devient
devient
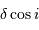 . Faire un schéma.
. Faire un schéma.
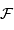 de longueur de longueur d'onde ?
de longueur de longueur d'onde ?
![I(\delta) \ = \ I_0 \ \left[1 + \cos(2\pi \sigma_1 \delta)\right] + I_0 \ \left[1 + \cos(2\pi \sigma_2 \delta)\right]](../pages_fourier/equations_fts-interferogramme/equation14.png)
![I(\delta) \ = \ 2\ I_0 \ \left[1 +\cos\bigl(\pi (\sigma_1+\sigma_2) \delta\bigr) \cos\bigl(\pi (\sigma_1-\sigma_2) \delta\bigr)\right]](../pages_fourier/equations_fts-interferogramme/equation15.png)
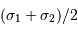 , modulé par une enveloppe de fréquence
, modulé par une enveloppe de fréquence 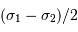 .
.
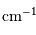 , soit une demi-différence de
, soit une demi-différence de 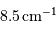 .
.
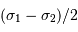 , la période spatiale est donc :
, la période spatiale est donc :
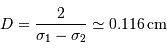
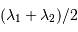 .
.