
|
Notion d'angle solide.
Définir l'étendue de faisceau ; mais surtout montrer la conservation de l'étendue de faisceau.
Un montage afocal transforme un faisceau plan en un autre faisceau plan. Les rapports des diamètres des faisceaux et des inclinaisons en entrée et sortie sont intimement liés au grossissement.
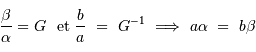
Le produit est un invariant, ce qui relate une relation physique plus générale : la conservation de l'énergie du faisceau.
La puissance (ou luminosité )
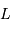 transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance
transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance 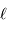 , à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
, à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
Un jeu d'écriture sur les grandeurs photométriques, avec les données de la figure, conduit à exprimer la conservation de la puissance lumineuse comme la conservation de l'étendue géométrique de faisceau. On définit cette étendue de faisceau, pour un faisceau traversant sans être collimaté (= sans perte d'énergie) un élément optique de section 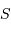 , occupant un angle solide
, occupant un angle solide 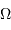 , dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit
, dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit 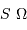 , qui se conserve le long du faisceau.
, qui se conserve le long du faisceau.
Pour les systèmes stigmatiques (càd, très grossièrement, donnant des images avec des aberrations limitées), la conservation de l'énergie se traduit par la conservation de l'étendue de faisceau :
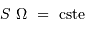
Le passage de la luminance 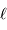 à la puissance lumineuse nécessite de s'appuyer sur le produit d'un élément de surface émetteur
à la puissance lumineuse nécessite de s'appuyer sur le produit d'un élément de surface émetteur 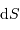 et d'un angle solide d'émission
et d'un angle solide d'émission 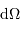 .
La luminosité élémentaire s'écrit :
.
La luminosité élémentaire s'écrit :
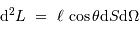
L'angle solide 'regarde' une surface réceptrice 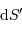 à la distance
à la distance 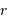 telle que :
telle que :
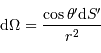
La luminosité élémentaire se réécrit donc :
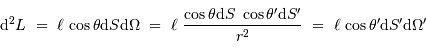
Avec 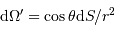 l'angle solide sous lequel est vue la source depuis la surface réceptrice. On remarque que le rôle des éléments émetteur et récepteur est symétrique. Le produit
l'angle solide sous lequel est vue la source depuis la surface réceptrice. On remarque que le rôle des éléments émetteur et récepteur est symétrique. Le produit 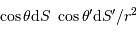 introduit l'étendue géométrique élémentaire.
introduit l'étendue géométrique élémentaire.
L'intégration sur le faisceau entier au travers d'une pupille, menée dans l'espace objet ou depuis l'espace image, garde la symétrie du produit surface 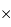 angle solide
angle solide 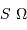 .
.
Un faisceau conique d'ouverture totale 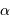 couvre un angle solide :
couvre un angle solide :
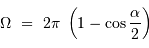
Si l'angle 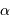 est petit, cet angle solide se réécrit simplement :
est petit, cet angle solide se réécrit simplement :
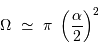
Au travers d'une optique de diamètre 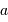 , la conservation du produit
, la conservation du produit 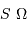 devient, pour ce faisceau conique :
devient, pour ce faisceau conique :
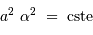
On retrouve donc le résultat obtenu dans le cadre du montage afocal.
Comme conséquences importantes, on note que :