 Prérequis
Prérequis
Notion d'angle solide.
 Objectifs
Objectifs
Définir l'étendue de faisceau ; mais surtout montrer la conservation de l'étendue de faisceau.
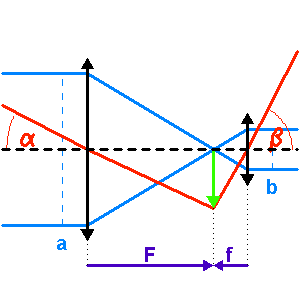
Le montage afocal transforme un faisceau de diamètre
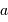
en un faisceau de diamètre
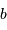
, avec un grossissement angulaire
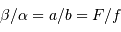
.
Crédit :
ASM
Exemple : montage afocal
Un montage afocal transforme un faisceau plan en un autre faisceau plan. Les rapports des diamètres des faisceaux et des inclinaisons en entrée et sortie sont intimement liés au grossissement.
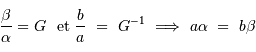
Le produit est un invariant, ce qui relate une relation physique plus générale : la conservation de l'énergie du faisceau.
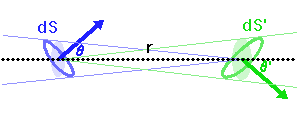
Conservation de l'étendue de faisceau, de l'élément émetteur
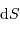
à l'aire collectrice
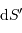
.
Crédit :
ASM
Faisceau, étendue de faisceau et conservation de l'énergie
La puissance (ou luminosité )
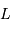 transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance
transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance 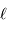 , à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
, à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
Un jeu d'écriture sur les grandeurs photométriques, avec les données de la figure, conduit à exprimer la conservation de la puissance lumineuse comme la conservation de l'étendue géométrique de faisceau. On définit cette étendue de faisceau, pour un faisceau traversant sans être collimaté (= sans perte d'énergie) un élément optique de section 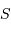 , occupant un angle solide
, occupant un angle solide 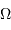 , dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit
, dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit 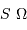 , qui se conserve le long du faisceau.
, qui se conserve le long du faisceau.
Pour les systèmes stigmatiques (càd, très grossièrement, donnant des images avec des aberrations limitées), la conservation de l'énergie se traduit par la conservation de l'étendue de
faisceau :
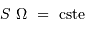
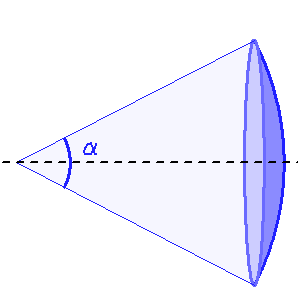
Faisceau divergeant d'une source quasi ponctuelle, collimaté : son énergie est localisée dans un cône.
Crédit :
ASM
Faisceau conique peu ouvert
Un faisceau conique d'ouverture totale 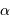 couvre un angle solide :
couvre un angle solide :
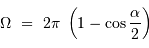
Si l'angle 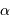 est petit, cet angle solide se réécrit simplement :
est petit, cet angle solide se réécrit simplement :
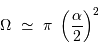
Au travers d'une optique de diamètre 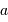 , la conservation du produit
, la conservation du produit 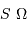 devient, pour ce faisceau conique :
devient, pour ce faisceau conique :
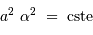
On retrouve donc le résultat obtenu dans le cadre du montage afocal.
Quelques conséquences
Comme conséquences importantes, on note que :
- Plus le faisceau collecté passe par un diamètre fin, plus il est divergent.
- Plus l'aire du collecteur est grande, plus l'étendue de faisceau est grande, plus les instruments doivent également être de grande taille pour offrir un grand diamètre au faisceau mis en forme.
- La surface du détecteur et l'angle solide qu'il peut voir (de l'ordre de l'angle d'ouverture du télescope) limitent nécessairement la taille angulaire du champ objet.
Etendue de faisceau cohérente
Un faisceau monochromatique est cohérent sur une étendue égale à 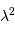 .
La justification est donnée en exercice.
.
La justification est donnée en exercice.
 Imagerie grand champ
Imagerie grand champ
Difficulté : ☆
Temps : 20 min
Le but d'une caméra est de réaliser un programme de cartographie, par imagerie grand champ. Les caractéristiques du détecteur sont fixées (taille du capteur CCD et caractéristiques de son optique), que l'on traduit par le produit 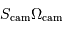 . Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
. Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
Question 1)
Comment varie la taille angulaire du champ objet en fonction de la surface 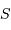 du collecteur ?
du collecteur ?
Se servir la conservation de l'étendue de faisceau
Question 2)
Le temps de pose est fixé par le rapport signal à bruit des observations, qui dépend essentiellement du nombre de photons collectés. Comment le temps de pose varie-t-il avec la surface du collecteur ?
Comment varie le nombre de photons collectés avec la surface collectrice ?
Question 3)
Y'a-t-il un intérêt particulier à utiliser un grand collecteur pour réaliser cette cartographie ? Quel usage peut-on conseiller à un télescope de la classe 4-m qui doit motiver son existence par rapport aux télescopes de nouvelle génération plus grands ?
Se servir des 2 questions précédentes.
Comparer la dépendance vis à vis de la surface collectrice 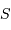 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.
 Sur les 2 tableaux
Sur les 2 tableaux
Difficulté : ☆☆
Temps : 20 min

Le montage optique réel de CoRoT. Les 2 miroirs paraboliques hors-axe sont notés Primary mirror et M2. Lens correspond à l'optique de chambre ; Focal box aux détecteurs CCD.
Crédit :
CNES
CoRoT est un satellite du CNES lancé en décembre 2006, qui poursuit 2 objectifs scientifiques : la recherche d'exoplanètes par la méthode des transits d'une part, l'étude sismique de quelques étoiles de type solaire d'autre part. Ces 2 objectifs s'appuient sur la capacité de CoRoT à mener des observations de photométrie très précises. Le montage optique retenu consiste en l'association de 2 miroirs paraboliques confocaux (confocal 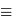 même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
Question 1)
Faire à l'échelle un schéma de principe le plus simple possible du système équivalent à l'ensemble miroirs + optique de chambre avec 3 lentilles équivalentes pour respectivement les 2 miroirs et l'optique de chambre.
Revoir la page sur le montage afocal.
Question 2)
Le diamètre du premier miroir vaut 30 cm ; les focales des miroirs primaire et secondaire sont dans un rapport de 3 à 1. Que peut-on en déduire concernant les lentilles de l'optique de chambre ? En quoi consiste l'un des intérêts de ce montage ?
Revoir (encore !) la page sur le montage afocal.
Question 3)
Reprendre le schéma de principe, en respectant l'ouverture du faisceau à 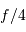 vu par la caméra, Calculer la focale
vu par la caméra, Calculer la focale 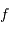 équivalente et la focale
équivalente et la focale 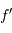 de l'optique de chambre.
de l'optique de chambre.
Question 4)
La question précédente met en évidence un gain sur l'optique de chambre. Mettre en évidence la contrainte associée, qui dérive de la conservation de l'étendue de faisceau. Conclure.
Simple application de la conservation de l'étendue de faisceau.
 Étendue cohérente
Étendue cohérente
Difficulté : ☆☆
Temps : 10 min
Un collecteur de diamètre 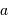 délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur)
délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur) 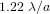 . On cherche à en déduire l'étendue de faisceau cohérente.
. On cherche à en déduire l'étendue de faisceau cohérente.
Question 1)
Justifier que l'étendue cohérente correspond au pic central de la diffraction.
Pourquoi le premier anneau de la tache de diffraction est-il noir? Que cela signifie-t-il ?
Question 2)
Déterminer l'étendue de faisceau cohérente. Montrer qu'elle est très voisine de
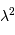 .
.
Revenir à la définition : exprimer 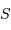 et
et 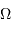 .
.
 D'un collecteur de 8 m à une fibre
D'un collecteur de 8 m à une fibre
Difficulté : ☆
Temps : 5 min
Un instrument du VLT (collecteur de diamètre 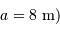 est alimenté par un faisceau de fibres de diamètre
est alimenté par un faisceau de fibres de diamètre 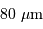 .
.
Question 1)
L'alimentation optimale de la fibre se fait à 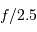 . En déduire l'ouverture angulaire du faisceau en entrée de fibre.
. En déduire l'ouverture angulaire du faisceau en entrée de fibre.
[1 points]
Question 2)
Que vaut le champ objet admissible sur le ciel ? L'exprimer en seconde d'angle.
[1 points]
 Observation au foyer et étendue de faisceau
Observation au foyer et étendue de faisceau
Difficulté : ☆☆
Temps : 15 min
On se propose de retrouver par l'application de la conservation de l'étendue de faisceau l'expression de la taille linéaire de l'image d'un objet à l'infini de diamètre angulaire 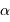 par un collecteur de diamètre
par un collecteur de diamètre 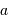 et de focale
et de focale 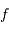 . On considère le seul cas où l'angle
. On considère le seul cas où l'angle 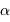 est petit. On note
est petit. On note 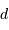 ladite taille linéaire.
ladite taille linéaire.
Question 1)
Exprimer le produit 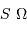 côté source, en fonction des données.
côté source, en fonction des données.
[1 points]
Question 2)
Rappeler l'expression de l'ouverture angulaire du collecteur, et exprimer le produit 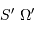 côté détecteur.
côté détecteur.
[2 points]
Question 3)
Exprimer la conservation de l'étendue de faisceau. Retrouve-t-on le résultat attendu ?
L'objet ayant une taille angulaire 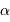 , quelle est la taille linéaire
, quelle est la taille linéaire 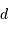 de son image.
de son image.
[2 points]
- Question 1
Aide :
Se servir la conservation de l'étendue de faisceau
Solution :
Si l'optique est bien conçue (sans diaphragme gênant), l'étendue
de faisceau se conserve. La traduction de 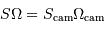 donne un angle solide objet
donne un angle solide objet
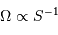
. Plus la
surface du collecteur est grande, plus le champ objet est réduit.
- Question 2
Aide :
Comment varie le nombre de photons collectés avec la surface collectrice ?
Solution :
Le nombre de photons collectés varie linéairement avec la surface collectrice. Le temps de pose varie donc en raison inverse :
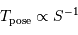
.
Plus la surface du collecteur est grande, plus le temps de pose est réduit.
- Question 3
Aide :
Se servir des 2 questions précédentes.
Aide :
Comparer la dépendance vis à vis de la surface collectrice 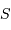 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.
Solution :
La taille angulaire du champ élémentaire accessible varie comme 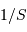 , la surface collectrice. Le temps de pose élémentaire varie comme
, la surface collectrice. Le temps de pose élémentaire varie comme 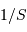 . Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée
. Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée 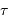 avec un petit collecteur sera observée par
avec un petit collecteur sera observée par 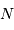 poses de durées
poses de durées 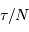 avec un grand.
avec un grand.
Notons que le télescope CFH, ouvert en 1980 avec un diamètre du collecteur de 3.6 m, s'est converti à partir des années 2000 vers l'imagerie grand champ.
- Question 1
Aide :
Revoir la page sur le montage afocal.
Solution :
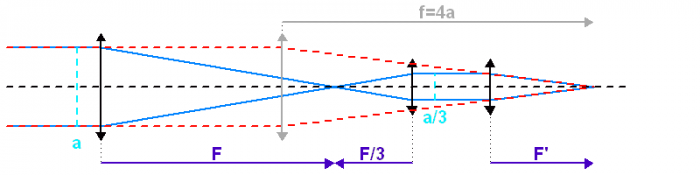
Le schéma équivalent correspond à un montage afocal suivi de l'optique de chambre
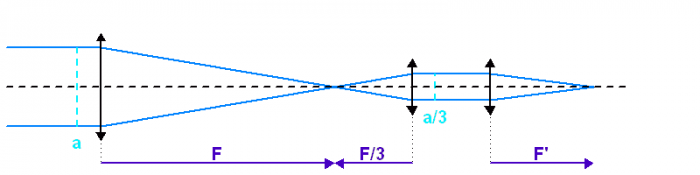
Ce montage afocal tient ici déjà compte de la suite, concernant le dimensionnement du miroir secondaire.
Crédit :
ASM
Remarque : pourquoi l'emploi des deux adjectifs, afocal et confocal, pour un même concept ? En fait, tout dépend du point de vue : si l'on s'intéresse aux dioptres, ils partagent un même foyer, d'où la dénomination confocale. Mais si l'on s'intéresse au faisceau, il passe de l'infini à l'infini, d'où la dénomination afocale.
- Question 2
Aide :
Revoir (encore !) la page sur le montage afocal.
Solution :
Par application directe des propriétés du montage afocal, le diamètre de la 2ème parabole comme celui des lentilles vaut le tiers de celui du primaire, soit 10 cm. Ce montage permet de réduire la taille des 6 lentilles de l'optique de chambre (intéressant en terme de poids et de coût). Mais, par conservation de l'étendue de faisceau, ces optiques travaillent sur des rayons d'inclinaison triplée.
- Question 3
Solution :
Le schéma équivalent demande 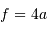 . L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
. L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
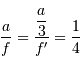
L'application numérique donne : 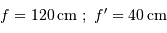
Le schéma équivalent demande
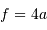
.
Crédit :
ASM
- Question 4
Aide :
Simple application de la conservation de l'étendue de faisceau.
Solution :
Par conservation de l'étendue de faisceau, la diminution du diamètre du faisceau par un facteur 3 s'accompagne par un accroissement dans un même facteur de l'ouverture.
Ainsi, le gain en taille doit être compensée par une meilleure qualité optique de ces lentilles travaillant avec rayons plus inclinés sur l'axe optique.
 Prérequis
Prérequis Objectifs
Objectifs
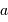 en un faisceau de diamètre
en un faisceau de diamètre 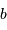 , avec un grossissement angulaire
, avec un grossissement angulaire 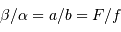 .
.
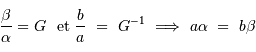

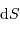 à l'aire collectrice
à l'aire collectrice 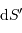 .
.
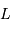 transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance
transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance 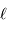 , à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
, à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
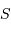 , occupant un angle solide
, occupant un angle solide 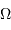 , dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit
, dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit 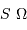 , qui se conserve le long du faisceau.
, qui se conserve le long du faisceau.
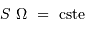
 Démonstration
Démonstration à la puissance lumineuse nécessite de s'appuyer sur le produit d'un élément de surface émetteur
à la puissance lumineuse nécessite de s'appuyer sur le produit d'un élément de surface émetteur 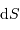 et d'un angle solide d'émission
et d'un angle solide d'émission 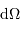 .
La luminosité élémentaire s'écrit :
.
La luminosité élémentaire s'écrit :
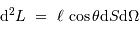
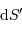 à la distance
à la distance 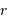 telle que :
telle que :
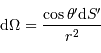
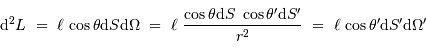
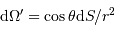 l'angle solide sous lequel est vue la source depuis la surface réceptrice. On remarque que le rôle des éléments émetteur et récepteur est symétrique. Le produit
l'angle solide sous lequel est vue la source depuis la surface réceptrice. On remarque que le rôle des éléments émetteur et récepteur est symétrique. Le produit 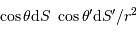 introduit l'étendue géométrique élémentaire.
introduit l'étendue géométrique élémentaire.
 angle solide
angle solide 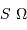 .
.

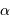 couvre un angle solide :
couvre un angle solide :
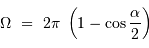
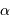 est petit, cet angle solide se réécrit simplement :
est petit, cet angle solide se réécrit simplement :
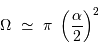
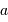 , la conservation du produit
, la conservation du produit 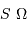 devient, pour ce faisceau conique :
devient, pour ce faisceau conique :
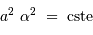
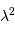 .
La justification est donnée en
.
La justification est donnée en 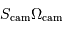 . Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
. Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
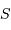 du collecteur ?
du collecteur ?
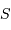 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.

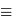 même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
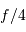 vu par la caméra, Calculer la focale
vu par la caméra, Calculer la focale 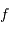 équivalente et la focale
équivalente et la focale 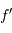 de l'optique de chambre.
de l'optique de chambre.
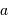 délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur)
délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur) 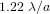 . On cherche à en déduire l'étendue de faisceau cohérente.
. On cherche à en déduire l'étendue de faisceau cohérente.
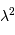 .
.
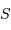 et
et 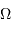 .
.
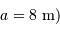 est alimenté par un faisceau de fibres de diamètre
est alimenté par un faisceau de fibres de diamètre 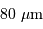 .
.
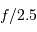 . En déduire l'ouverture angulaire du faisceau en entrée de fibre.
. En déduire l'ouverture angulaire du faisceau en entrée de fibre.
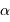 par un collecteur de diamètre
par un collecteur de diamètre 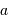 et de focale
et de focale 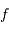 . On considère le seul cas où l'angle
. On considère le seul cas où l'angle 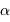 est petit. On note
est petit. On note 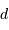 ladite taille linéaire.
ladite taille linéaire.
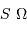 côté source, en fonction des données.
côté source, en fonction des données.
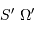 côté détecteur.
côté détecteur.
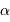 , quelle est la taille linéaire
, quelle est la taille linéaire 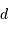 de son image.
de son image.
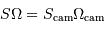 donne un angle solide objet
donne un angle solide objet
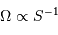
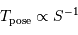
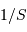 , la surface collectrice. Le temps de pose élémentaire varie comme
, la surface collectrice. Le temps de pose élémentaire varie comme 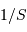 . Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée
. Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée 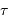 avec un petit collecteur sera observée par
avec un petit collecteur sera observée par 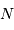 poses de durées
poses de durées 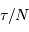 avec un grand.
avec un grand.

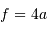 . L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
. L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
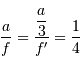
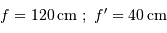

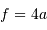 .
.
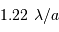 , couvre un angle solide de l'ordre de :
, couvre un angle solide de l'ordre de :
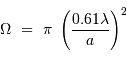
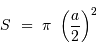
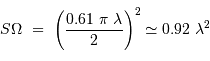
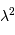 .
.