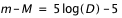Les distances des galaxies
Auteur: Florence Durret
- Les mesures de distances : introduction
- Les parallaxes des étoiles proches
- Calcul de la distance d'une étoile proche
- Un premier indicateur de distances : les étoiles Céphéides
- Magnitude absolue
- Les deux différents types de Céphéides
- Distance d'Andromède calculée avec les Céphéides
- Un deuxième indicateur de distances : les supernovae
- La mesure des distances par spectroscopie
- Exercice: calcul du décalage spectral et de la distance d'une galaxie
Les mesures de distances : introduction
Afin de connaître les propriétés des galaxies, il est nécessaire de pouvoir déterminer leur distance. En effet, nous pouvons seulement effectuer des mesures en pixels sur le CCD qui nous sert de récepteur. Connaissant la dimension angulaire d'un pixel en projection sur le ciel, nous pouvons alors calculer les angles correspondants, toujours en projection dans le plan du ciel. Pour transformer ces mesures angulaires en distances physiques, il est ensuite nécessaire de connaître la distance de l'objet.
Les distances des galaxies proches sont souvent exprimées en Mpc (Megaparsecs).
Le parsec est une unité de longueur correspondant à la distance à laquelle la parallaxe d'une étoile est de 1 seconde d'arc (1 seconde d'angle vaut 1/3600 ème de degré).
La correspondance entre parsec (pc) et année lumière (a-l) est : 1 pc = 3,26 al. Le kpc (kiloparsec), qui vaut 1000 pc, est une unité commode pour les distances au sein d'une galaxie, et le Mpc (mégaparsec) sert à exprimer les distances des galaxies proches (ou les dimensions des amas de galaxies).
Pour mesurer les distances des galaxies, on utilise ce que l'on appelle des indicateurs de distance. Il s'agit de propriétés qui sont les mêmes pour une catégorie d'objets donnés, et qui permettent de proche en proche d'estimer la distance des galaxies. Pour des galaxies de plus en plus lointaines, on distingue ainsi les indicateurs primaires, secondaires, et tertiaires.
Les parallaxes des étoiles proches
La première manière de déterminer la distance d'une étoile proche est de mesurer ce que l'on appelle sa parallaxe.
Parallaxe
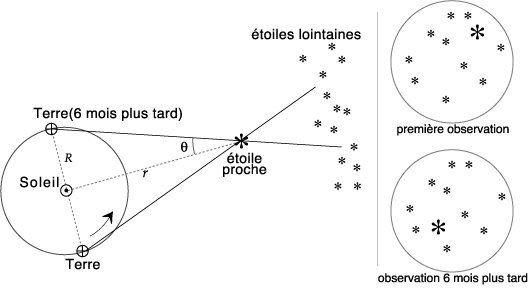
Schéma montrant comment on définit la parallaxe d'une étoile
Crédit :
G.B. Lima Neto, cours Université de São Paulo, Brésil
Parallaxe d'une étoile proche
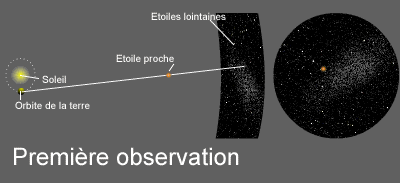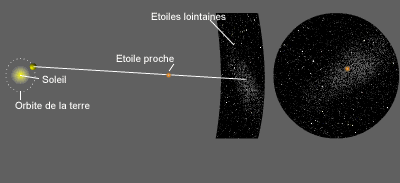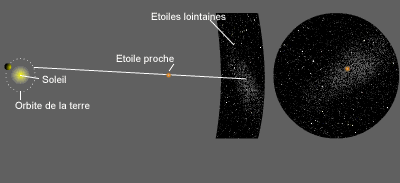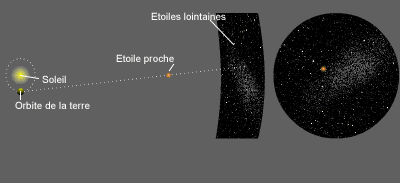
Animation illustrant la notion de parallaxe : il s'agit de l'angle sous lequel depuis une étoile proche on verrait le rayon de l'orbite terrestre. L'image de droite montre la projection a 90° de celle de gauche, autrement dit le mouvement de l'étoile proche dans le plan du ciel.
Echelles de distances dans l'Univers
Crédit :
ASM
Lorsque la Terre est dans une certaine position, par exemple à l'équinoxe de printemps, elle voit l'étoile proche dans une certaine direction dans le ciel (par rapport à des étoiles lointaines). Six mois plus tard, à l'équinoxe d'automne, la même étoile semblera s'être déplacée par rapport aux étoiles lointaines (qui, elles, n'auront pas bougé).
Si l'on connaît les propriétés optiques de l'ensemble télescope +caméra+détecteur, on peut estimer de quel angle sur le ciel l'étoile s'est déplacée par rapport aux étoiles lointaines et fixes d’arrière plan.
On peut alors mesurer de combien l'étoile proche s'est déplacée par rapport aux étoiles lointaines et fixes d'arrière-plan.
Ainsi, connaissant les propriétés optiques de l'instrument utilisé (télescope + détecteur), on peut calculer la dimension du pixel en secondes d’angle (1 second d'arc vaut la 3600ème partie d'un degré d'angle). On peut donc mesurer 2 theta, où theta est la parallaxe de l'étoile (voir schéma ci-dessus).
On peut écrire :
tan θ = ST / SE, et comme θ est un angle très petit on peut l'assimiler à sa tangente, à condition de le convertir en radians.
D'où:
θ (rad) = ST/SE.
Comme on connaît ST (distance moyenne Terre-Soleil) et que l'on peut mesurer θ, on en déduit SE = distance de l’étoile au Soleil (ou à la Terre, la différence est minime).
La difficulté d'appliquer cette méthode est due au fait que les parallaxes θ sont des angles très petits, donc difficiles à mesurer, et seulement mesurables pour les étoiles proches. Au-delà les angles deviennent trop petits et impossibles à mesurer.
Le satellite Hipparcos a mesuré les parallaxes, et donc les distances d'environ 100.000 étoiles au début des années 1990, et le futur satellite Gaia devrait en mesurer dix fois plus d'ici quelques années. Il est très important de bien connaître la distance des étoiles, car il devient alors possible d'estimer leurs propriétés intrinsèques à partir des observations.
Calcul de la distance d'une étoile proche
 Distance d'une étoile d'après sa parallaxe
Distance d'une étoile d'après sa parallaxe
Difficulté : ☆
Temps : 2 minutes
Question 1)
Une étoile est vue sous une parallaxe de 0,1 seconde d'angle. Calculer sa distance en mètres, puis en parsecs.
Se rappeler la définition de la parallaxe d'une étoile. La distance moyenne Terre-Soleil est d'environ 150 000 000 km. La seconde d'angle vaut 1/3600ème de degré d'angle. Il faut exprimer la parallaxe en radians.
Question 2)
Comment aurait-on pu trouver ce résultat sans aucun calcul ?
Se rappeler la définition de la parallaxe.
Un premier indicateur de distances : les étoiles Céphéides
Au début du XXème siècle, l'astronome américaine Henrietta Leavitt découvrit et caractérisa un nouveau type d'étoiles variables : les Céphéides, du nom de leur prototype, l'étoile delta de la constellation de Cephée.
delta Céphée
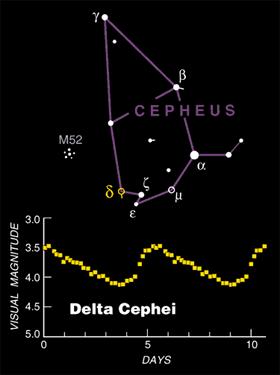
Schéma montrant la position de l'étoile delta de la constellation de Céphée et en-dessous sa courbe de lumière (
magnitude apparente en fonction du temps, exprimé en jours).
Crédit :
G.B. Lima Neto, cours Université de São Paulo, Brésil
L'éclat de ces étoiles varie de manière périodique, et la période P de ces variations est d'autant plus courte que l'éclat moyen est faible.
H. Leavitt montra qu'il existait une relation du type
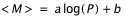
où <M> est la magnitude absolue de l'étoile (par définition sa magnitude si elle était située à une distance de 10 pc), et a et b sont des constantes.
Grâce à l'observation d'étoiles Céphéides dont la distance avait été mesurée par une autre méthode (par exemple par leur parallaxe), il a été possible de calculer a et b, la valeur de M étant déduite de la magnitude apparente par la relation :
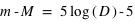 où D est la distance de l'étoile mesurée en pc.
où D est la distance de l'étoile mesurée en pc.
La connaissance de a et b, la mesure de la période P et de la magnitude apparente m d'une Céphéide située à une distance inconnue, permet alors de calculer sa magnitude absolue, et donc sa distance.
Les Céphéides sont des indicateurs de distance très précieux, aussi appelés "chandelles standards".
La quantité m-M est appelée "module de distance"
Magnitude absolue
 Magnitude absolue
Magnitude absolue
Question 1)
Retrouver la définition de la magnitude absolue M d'après la relation
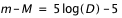
Calculer la distance pour laquelle on a M=m.
Question 2)
Si le module de distance d'une galaxie est 30, quelle est sa distance? (bien préciser l'unité)
Se rappeler que le module de distance est la quantité m-M.
Les deux différents types de Céphéides
On a cependant remarqué que la relation entre la magnitude apparente et la période présentait une certaine dispersion, et en étudiant de manière précise les Céphéides on a découvert qu'il en existait en fait de deux types, correspondant à deux séquences légèrement différentes. Ceci a permis d'affiner la relation période-luminosité des Céphéides, et donc d'améliorer la précision sur les distances mesurées grâce à ces étoiles.
Récemment, un grand programme d'observations a été consacré aux Céphéides par une équipe américaine avec le télescope spatial Hubble, et a conduit à une détermination plus précise de la constante de Hubble (voir plus loin).
Céphéides 1960
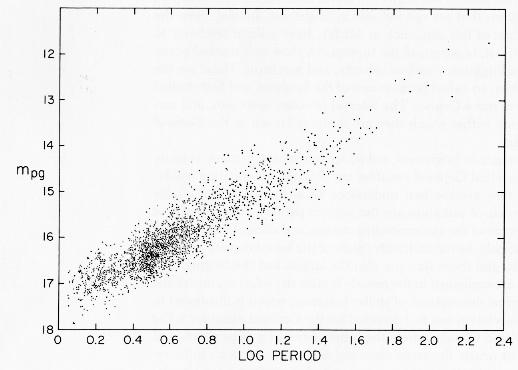
La relation période-luminosité des Céphéides dans les années 1960. On remarque que les étoiles varient d'autant moins vite (longue période) qu'elles sont plus brillantes (faible magnitude).
Crédit :
Scienza Per Tutti, http://scienzapertutti.Inf.infn.it/risposte/ris271.html
Céphéides 1990
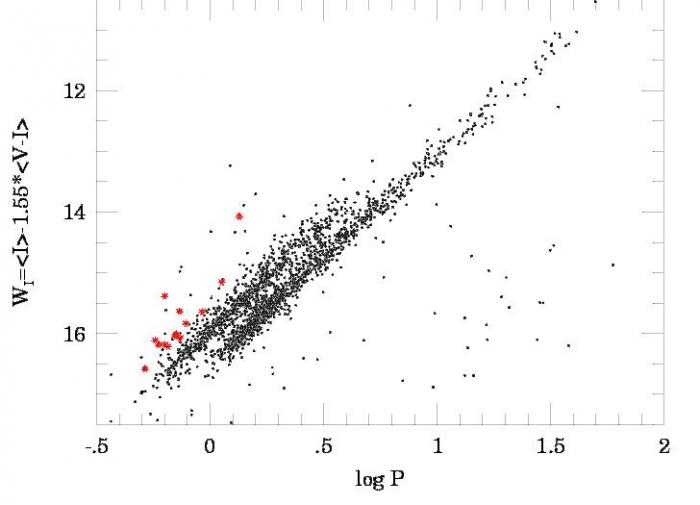
La relation période-luminosité des Céphéides dans les années 1990 : deux séquences sont clairement visibles
Crédit :
Scienza Per Tutti, http://scienzapertutti.Inf.infn.it/risposte/ris271.html
Distance d'Andromède calculée avec les Céphéides
 Calibration de la relation période-luminosité des Céphéides
Calibration de la relation période-luminosité des Céphéides
Difficulté : ☆
Temps : 1 minute
Question 1)
La relation période-luminosité des étoiles Céphéides relie leur période de variation à leur magnitude absolue. Comment peut-on connaître la magnitude absolue de ces étoiles?
Il faut mesurer la période de Céphéides dont on a pu mesurer la distance par une autre méthode, par exemple par leur parallaxe. Ceci permet de calculer les quantités a et b dans la relation <M>=a logP+b.
Question 2)
Pourquoi avait-on jusque récemment une assez grande dispersion dans la relation période-luminosité des Céphéides?
Se souvenir que si une relation présente une forte dispersion, c'est peut-être parce qu'on mélange des objets ayant des propriétés différentes.
Un deuxième indicateur de distances : les supernovae
Une supernova est une étoile massive qui explose à la fin de son évolution. La courbe de lumière d'une supernova, représentant sa magnitude apparente en fonction du temps, consiste en une partie où l'éclat de l'étoile croît très rapidement, puis une décroissance rapide de l'éclat, suivie ensuite d'une décroissance beaucoup plus lente.
Il existe des supernovae de plusieurs types, parmi lesquels les supernovae de type Ia (SNIa) dont la magnitude absolue au maximum d'éclat est quasiment la même pour toutes ces étoiles. On peut donc les utiliser comme indicateurs de distance.
SN Ia
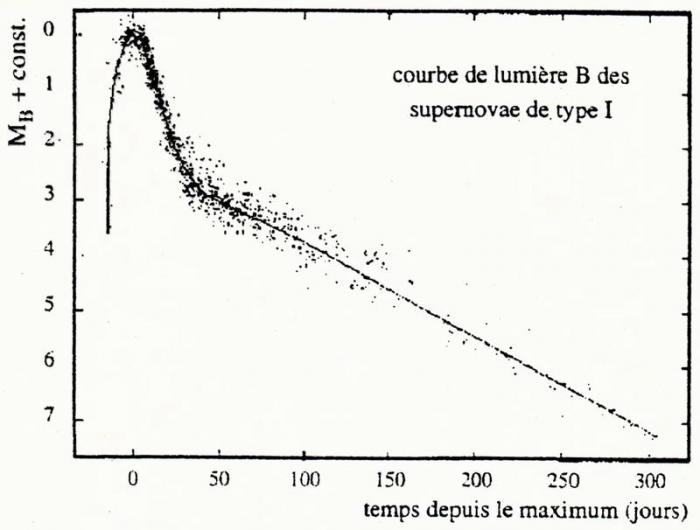
Courbe de lumière typique d'une supernova de type Ia, avec le temps en abscisses et la magnitude en ordonnées.
Crédit :
Alain Bouquet, cours en ligne
SNIa plusieurs
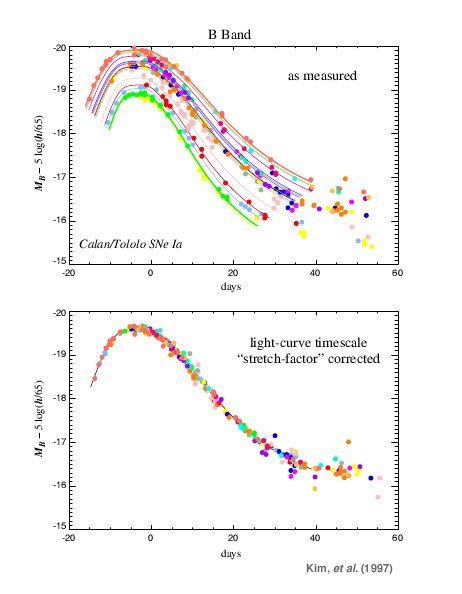
Courbes de lumière de différentes supernovae avant correction (en haut) et après correction (en bas)
Crédit :
Cosmologie & Supernovae de type Ia, Cours de Pierre Antilogus, ireswww.in2p3.fr/ires/seminaires/GIF/cours/cours_2a.pdf
En réalité il existe une certaine dispersion entre les courbes de lumière des SNIa, que l'on peut réduire en tenant compte de diverses autres corrélations entre la magnitude absolue au maximum d'éclat et d'autres quantités, en particulier la pente de la décroissance de la courbe de lumière après le maximum. On obtient alors une relation analogue à la relation période-luminosité des Céphéides, qui sert d'indicateur de distance pour des galaxies beaucoup plus lointaines, puisque les supernovae sont des objets intrinsèquement très brillants, et que l'on peut donc voir très loin.
On a ainsi pu construire de proche en proche des échelles de distances pour mesurer les distances des galaxies, aboutissant à la loi de Hubble qui permet de calculer la distance des galaxies à partir de leur décalage spectral, comme décrit ci-dessous.
La mesure des distances par spectroscopie
Dans les années 1920, l'astronome américain Edwin Hubble prit les premiers spectres de galaxies et découvrit que ces spectres étaient décalés vers les grandes longueurs d'onde (c'est à dire vers les longueurs d'onde rouges du spectre visible) par rapport aux spectres du Soleil ou d'étoiles de notre Galaxie.
Il interpréta ce phénomène comme l'équivalent pour la lumière de l'effet Doppler pour les ondes sonores : si la source s'éloigne de l'observateur, la fréquence de l'onde reçue devient plus basse (et donc la longueur d'onde devient plus grande) que celle de l'onde émise.
Le décalage vers le rouge des spectres des galaxies indique donc que les galaxies s'éloignent les unes des autres, et donc que l'univers est en expansion.
Spectres de deux galaxies
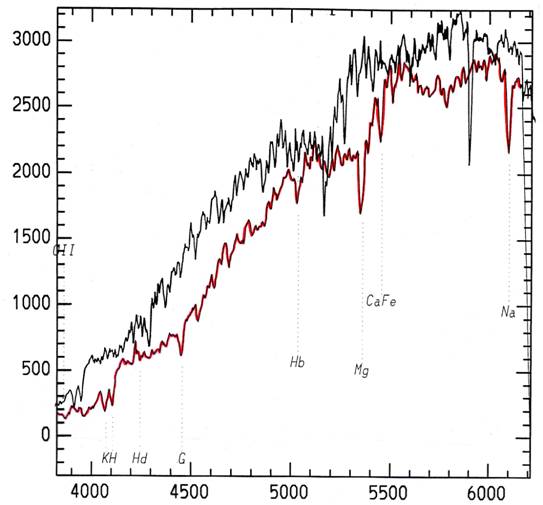
Spectre d'une galaxie proche (en noir) servant de référence, et d'une galaxie dont on veut mesurer le décalage spectral (en rouge)
Crédit :
Florence Durret
En mesurant le décalage spectral (redshift en Anglais) de galaxies proches dont la distance avait été déterminée par exemple grâce aux Céphéides, Hubble a montré que le décalage spectral était proportionnel à la distance de la galaxie.
Cette relation est maintenant appelée loi de Hubble.
Pour une raie de longueur d'onde λ0 mesurée à la longueur d'onde λ dans le spectre de la galaxie, le décalage spectral est par définition :
z = ( λ - λ0 ) / λ0
La vitesse à laquelle la galaxie s'éloigne de nous est alors v = c.z où c est la vitesse de la lumière. Cette formule n'est valable que pour les galaxies proches, lorsque le décalage spectral reste faible (si l'on appliquait cette formule pour un décalage spectral supérieur à 1, la vitesse de récession des galaxies deviendrait supérieure à celle de la lumière).
La distance d'une galaxie est alors simplement D = v/H0 où H0 est la constante de Hubble.
Pour des décalages spectraux plus grands, il faut appliquer des formules prenant en compte la relativité d'Einstein.
Loi de Hubble
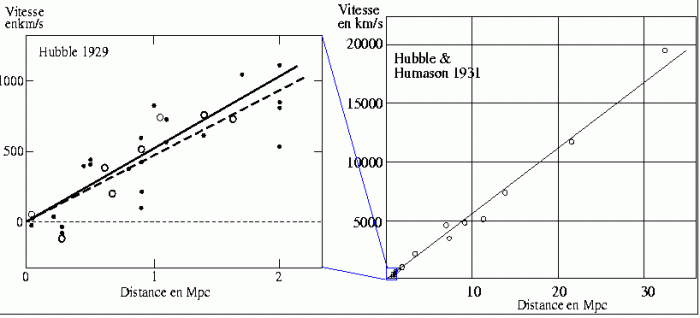
Relation entre la vitesse de récession d'une galaxie et sa distance, maintenant appelée loi de Hubble.
Crédit :
Figure de gauche : Hubble E.P. 1929, ApJ 69, 103 ; figure de droite : Hubble E.P. & Humason M.L. 1931, ApJ 74, 43
En 1929, Hubble détermina pour la première fois la valeur de la constante qui porte maintenant son nom, en observant des galaxies distantes de moins de 2 Mpc. La dispersion des points était grande et la valeur de la constante qu'il trouvait était de l'ordre de 500 km s -1 Mpc -1. Deux ans plus tard, avec Humason, Hubble étendit cette relation à des galaxies 15 fois plus lointaines. Cependant, la valeur de la constante restait à peu près identique (et donc fausse par un facteur de l'ordre de 10).
Durant le XXème siècle il y eut de nombreuses observations pour améliorer la précision sur la détermination de la constante de Hubble.
Ainsi, deux équipes s'affrontèrent pendant des années, celle autour de Gérard de Vaucouleurs prônant H0 = 100km s-1 Mpc-1 tandis qu'une autre équipe autour de Sandage et Tammann trouvait plutôt H0 = 50 km s -1 Mpc -1.
La valeur actuellement admise est 72 km s-1 Mpc-1. Elle a été déterminée à partir d'un grand programme d'observations avec le télescope spatial Hubble par l'équipe de Wendy Freeman. L'erreur sur cette valeur est de l'ordre de quelques unités.
Exercice: calcul du décalage spectral et de la distance d'une galaxie
 Calcul du décalage spectral et de la distance d'une galaxie proche
Calcul du décalage spectral et de la distance d'une galaxie proche
Difficulté : ☆
Temps : 2 minutes
Question 1)
La longueur d'onde en laboratoire de la raie Hα de l'hydrogène ionisé est 656.28 nm.
On détecte cette raie dans le spectre d'une galaxie à la longueur d'onde de 662.85 nm. Quel est le décalage spectral de la galaxie ?
Se rappeler que le décalage spectral est le décalage relatif d'une raie par rapport à sa position mesurée en laboratoire.
Question 2)
Si l'on prend comme constante de Hubble 70 km s-1 Mpc-1, a quelle vitesse la galaxie s'éloigne-t-elle de nous et quelle est sa distance (on négligera les effets relativistes) ?
A faible décalage spectral z, la vitesse à laquelle s'éloigne la galaxie est le produit de z par la vitesse de la lumière. La distance de la galaxie est proportionnelle à la vitesse de la galaxie. Se rappeler la définition de la constante de Hubble et faire attention aux unités.
Réponses aux exercices
pages_galaxies/exercice-parallaxe.html
Exercice
'Distance d'une étoile d'après sa parallaxe'
- Question 1
Aide :
Se rappeler la définition de la parallaxe d'une étoile. La distance moyenne Terre-Soleil est d'environ 150 000 000 km. La seconde d'angle vaut 1/3600ème de degré d'angle. Il faut exprimer la parallaxe en radians.
- Question 2
Aide :
Se rappeler la définition de la parallaxe.
pages_galaxies/exo-magabs.html
Exercice
'Magnitude absolue'
pages_galaxies/exercice-cepheides.html
Exercice
'Calibration de la relation période-luminosité des Céphéides'
- Question 1
Aide :
Il faut mesurer la période de Céphéides dont on a pu mesurer la distance par une autre méthode, par exemple par leur parallaxe. Ceci permet de calculer les quantités a et b dans la relation <M>=a logP+b.
- Question 2
Aide :
Se souvenir que si une relation présente une forte dispersion, c'est peut-être parce qu'on mélange des objets ayant des propriétés différentes.
pages_galaxies/exercice-redshift.html
Exercice
'Calcul du décalage spectral et de la distance d'une galaxie proche'
- Question 1
Aide :
Se rappeler que le décalage spectral est le décalage relatif d'une raie par rapport à sa position mesurée en laboratoire.
- Question 2
Aide :
A faible décalage spectral z, la vitesse à laquelle s'éloigne la galaxie est le produit de z par la vitesse de la lumière. La distance de la galaxie est proportionnelle à la vitesse de la galaxie. Se rappeler la définition de la constante de Hubble et faire attention aux unités.



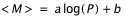
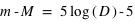 où D est la distance de l'étoile mesurée en pc.
où D est la distance de l'étoile mesurée en pc.