Ce cours introduit la théorie de la gravitation et la notion d’ondes gravitationnelles (comment elles se forment, comment elles se propagent, comment on les détecte). Les ondes gravitationnelles sont introduites par analogie avec les ondes électromagnétiques. L’électromagnétisme a donc une place importante dans notre présentation.
Nous nous plaçons dans une perspective historique et commençons par nous demander pourquoi une pomme tombe au sol alors que la Lune ne le fait pas. Autrement dit, ce questionnement remonte aux reflexions d’Aristote.
NB : Les figures sans notification de crédit sont de l'auteur.
14/11/2022 :version beta du cours. Merci d'envoyer vos remarques à : contact point asm arobase obspm.fr
Mouvements naturels et violents
Aristote distinguait deux types de mouvements : les mouvements naturels, qui se passent tout seuls, et les mouvements violents, qui nécessitent l’action d’une force (le mot violent vient de vis, la force en latin*). Il est naturel que les pommes chutent d’un arbre. En revanche, les pommes ne se lèvent jamais toutes seules du sol pour aller dans un cageot. Pour cela il faut une action externe, la force de la main de l’agriculteur qui les cueille et les met dans le cageot.
Aristote

Crédit :
S.Cnudde
Aristote

Crédit :
S. Cnudde
La gravité comme propriété des corps
Pourquoi serait-il naturel qu'une pomme chute ? Pour Aristote, la pomme chute à cause de son poids. En latin, lourd se dit gravis. Pour Aristote, la gravité, c'est-à-dire le poids, est une caractéristique de la pomme. Il fait partie de sa nature. Le feu est léger. C'est pour cela que les flammes ne chutent pas, mais elles montent vers le ciel.
De différentes lois de la nature pour les corps terrestres et les corps célestes
Aristote étendait sa théories aux corps céleste. Pour lui, la Lune ne chute pas parce qu'elle n'est pas faites de roches comme la Terre. Elle se compose d'un substance imponderable qu'Aristote appelait quintessence. La gravité est étrangère à sa nature.
* Aristote écrivait en grec, mais notre présentation est en français, qui est une langue latine. C'est donc l'étimologie de mots français utilisés pour traduire Aristote qui est pertinente.
La gravité est une force
Newton révolutionne cette vision. La pesanteur n’est pas une qualité intrinsèque de la pomme. Elle est due à l’attraction gravitationnelle que la Terre exerce sur la pomme, et, plus généralement, que tous les corps exercent les uns sur les autres.
Newton

Crédit :
S. Cnudde
La gravité agit de la même manière sur tous les corps
Pour Newton (et déjà Galilée, avant lui), il n'y a pas de différence entre les corps terrestres et les corps célestes. Les lois de la physique sont les mêmes pour les uns comme pour les autres. La pomme chute dans la direction du corps massif qui l’attire. Si on la laissait tomber sur la Lune, elle chuterait sur le sol lunaire.
La gravité est une force à distance
La notion d’attraction gravitationnelle nous est tellement familière que nous n’en percevons plus le caractère novateur. Mais, pour les contemporains de Newton, et pour Newton même qui l’avait proposée, la notion d’une force qui agit : i) d’une manière instantanée, ii) à distance et iii) même sur des objets qui n’ont aucun contact avec la Terre, apparaissait très troublante et s’approchait plus de la sorcellerie que de la science.
Dans une lettre au révérend Richard Bentley, en 1692, Newton écrivit : « C’est inconcevable que de la matière inanimée, sans la médiation d’aucun autre corps matériel, puisse agir sur un autre sans aucun contact réciproque. Que la gravité soit innée, inhérente et essentielle à la matière, de sorte qu’un corps puisse agir sur un autre à travers le vide, sans la médiation de quelque chose d’autre, grâce et à travers laquelle cette action et cette force puissent être transmises de l’un à l’autre, est pour moi une absurdité tellement grande que je ne crois pas que personne ayant des facultés mentales compétentes en matière de philosophie puisse y tomber dedans. La gravité doit être causée par un agent qui agit constamment selon certaines lois ; mais, si cet agent est matériel ou immatériel, je l’ai laissé à la considération de mes lecteurs. »
La théorie des vortex de Descartes (comme d’autres théories mécaniques de la gravité, par exemple celle proposée par Nicolas Fatio et Georges-Louis Le Sage) est une tentative d’expliquer la gravité sans faire intervenir l’action à distance. Pour Descartes, comme pour Aristote, le vide n’existait pas. L’espace que nous appelons vide est rempli d’un fluide transparent de faible densité, l’éther. A cause du principe d’inertie, chaque élément d’éther tend à se déplacer suivant une ligne droite, mais l’interaction avec les éléments environnants transforme le mouvement rectiligne en mouvement circulaire. Selon Descartes, les corps célestes seraient entraînés dans leurs mouvements circulaires par des tourbillons dans l’éther. Les tourbillons pousseraient les corps terrestres vers le bas, déterminant leur chute.
Ces théories ont été abandonnées à cause de leur conflit avec les données d’observation, mais elles démontrent à quel point la notion d’action instantanée à distance était perçue comme insatisfaisante. Elles étaient de mauvaises réponses, mais la question à laquelle elles essayaient de répondre était très pertinente.
Les ondes gravitationnelles sont la réponse de la théorie de la relativité d’Einstein au problème de comment l’interaction gravitationnelle est capable de se propager à distance dans le vide.
D'autres exemples de forces à distance
L’attraction gravitationnelle n’est pas la seule force à distance. Il y a aussi les forces magnétiques et électriques. Depuis l’antiquité, on savait que les aimants attirent le fer et que l’ambre est capable d’attirer les poils de chat après que les deux ont été électrisés par frottement (par ailleurs, « électricité » vient d’elektron, le mot grec pour l’ambre).

Magnétisme : L'aimant attire le fer
Crédit :
S. Cnudde

Electricité : l’ambre attire les poils de chat électrisés par frottement
Crédit :
S. Cnudde
La découverte des ondes électromagnétiques prépare celle des ondes gravitationnelles
Ici, nous discuterons des forces électriques et magnétiques en détail, même si cette discussion pourrait paraître hors sujet, parce que le problème de l’action à distance a été résolu d’abord, au 19ème siècle, pour les forces électromagnétiques. Puis, la théorie électromagnétique a préparé le terrain pour le développement, au 20ème siècle, du concept d’ondes gravitationnelles.
L'électricité est le phénomène par lequel deux charges de signe opposé s'attirent alors que deux charges du même signe se repoussent.
Commençons donc par considérer deux charges électriques, une charge très grande Q et une charge très petite q. Nous choisissons deux charges très différentes, plutôt que deux charges comparables, parce que nous souhaitons pouvoir négliger l’action de la petite charge sur la grande charge, de la même façon que l’on considère l’effet de la Terre sur le mouvement d’une pomme, mais on néglige les effets de la pomme sur le mouvement de la Terre.
La loi de Coulomb affirme que la charge Q exerce sur la charge q une force 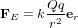 , où r est la distance qui sépare les charges,
, où r est la distance qui sépare les charges, 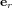 est un vecteur de longueur unitaire dirigé de Q vers q et
est un vecteur de longueur unitaire dirigé de Q vers q et 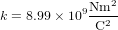 est la constante de Coulomb (en unités du Système International, où le newton est l'unité de force, le mètre est l'unité de longeur et le coulombs est l'unité pour la quantité de charge).
est la constante de Coulomb (en unités du Système International, où le newton est l'unité de force, le mètre est l'unité de longeur et le coulombs est l'unité pour la quantité de charge). 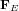 est positive (répulsive) si les deux charges ont le même signe et négative (attractive) si elles ont des signes opposés.
est positive (répulsive) si les deux charges ont le même signe et négative (attractive) si elles ont des signes opposés.
La figure ci-dessous montre la force électrique 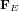 que la charge Q exerce sur la charge q pour différentes positions de cette dernière. La force est plus intense quand la distance r entre q et Q est plus petite. Le module du vecteur
que la charge Q exerce sur la charge q pour différentes positions de cette dernière. La force est plus intense quand la distance r entre q et Q est plus petite. Le module du vecteur 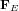 est quatre fois plus grand quand la distance entre q et Q est deux fois plus petite.
est quatre fois plus grand quand la distance entre q et Q est deux fois plus petite.
Lignes de force du champs électrique
De la même manière que nous avons tracé la force 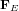 pour différentes positions de la charge q, nous pouvons tracer les lignes de force pour le champ électrique
pour différentes positions de la charge q, nous pouvons tracer les lignes de force pour le champ électrique 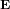 , qui donnent sa direction en chaque point de l’espace.
, qui donnent sa direction en chaque point de l’espace.
La figure ci-dessous montre les ligne de forces pour : a) une charge isolée positive ; b) un système composé par deux charges égales en valeur absolue mais de signes opposés. Cette figure utilise la couleur bleue pour les charges positives et la couleur rouge pour les charges négatives.
Les lignes de forces sortent des charges positives et rentrent dans les charges négatives. Les charges sont donc les sources du champ électrique, où les lignes de force commencent et se terminent. Le champ électrique est plus intense où les lignes de force sont plus denses, c'est-à-dire plus proches les unes des autres.
Une région d’espace vide, comme celle enfermée par la surface S dans la figure ci-dessus, peut contenir des lignes des forces, mais elle ne peut contenir aucun point à partir duquel les lignes de force divergent ou vers lequel les lignes de force convergent.
Un courant est un mouvement de charges
Jusqu’à maintenant, nous avons considéré le champ électrique produit par des charges statiques. Maintenant, nous devons considérer le cas plus compliqué des courants, c’est-à-dire, de charges en mouvement.
Du pôle positif au pôle négatif
Prenons le cas tout simple d’une pile. Si nous raccordons le pôle positif et le pôle négatif de la pile avec un fil métallique (figure ci-dessous), un courant passera dans le fil jusqu’à ce que la pile se décharge, alors que le fil se réchauffe (l'énergie stockée dans la pile est transformée en chaleur). Par définition, le courant va toujours du pôle positif vers le pôle négatif (le sens de la fleche orange).
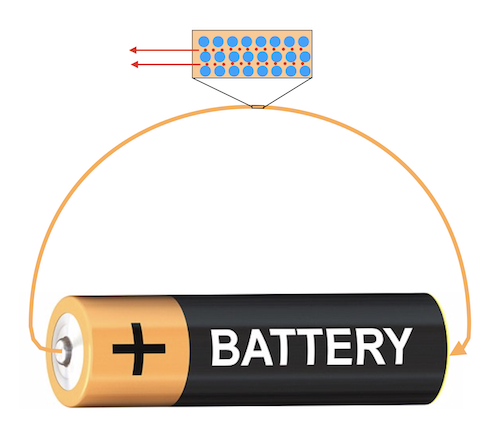
Le courant dans un fil est dû au mouvement des électrons (dans le sens inverse)
Par définition, le courant va toujours du pôle positif vers le pôle négatif (le sens de la fleche orange). Cependant, cette direction conventionnelle est un héritage d'une époque où la structure microscopique des courants était encore inconnue et ne reflète pas le sens physique du mouvement. Aujourd'hui, nous savons qu'un métal est composé de noyaux atomiques et d'électrons, qui remplissent l'espace entre les noyaux (la figure ci-dessus montre un agrandissement d'un petit morceau de fil ; dans cet agrandissement les noyaux atomiques sont montrés en bleu et les électrons en rouge). Les noyaux ont une charge positive. Les électrons ont une charge négative. Le courant est le mouvement des électrons dans le fil : le pôle négatif de la pile repousse ses électrons dans le fil ; les électrons se se déplacent dans le fil et en sortent par le pôle positif de la pile, qui les attire.
Les fils électriques sont neutres (même s'ils contiennent des charges)
Globalement, le fil est neutre, parce qu’il contient le même nombre de charges positives (de protons) et de charges négatives (d’électrons), donc il ne produit aucun champ électrique. Cela n’empêche pas qu’il y ait un mouvement des charges négatives par rapport aux charges positives.
Pour illustrer ce concept, on pourrait comparer le fil à une grande salle d’attente, dans laquelle il y a le même nombre d’hommes et de femmes. Les hommes sont toujours là. Aucun ne bouge de sa chaise. Mais toutes les dix minutes, une femme sort et une autre rentre à sa place. Le rapport hommes/femmes dans la salle reste égal à 1, mais il y a un mouvement des femmes mais pas des hommes. Dans cette métaphore, les hommes sont les protons, les femmes sont les électrons qui se déplacent plus facilement dans le métal et qui donc transportent le courant. L'importance de ce mouvement relatif deviendra bientôt évidente, alors que nous parlerons des champs magnétiques.
Un courant génère un champ magnétique
Les courants ne produisent pas de champs électriques, donc elles n'ont aucune influence sur les charges statiques. Mais, déjà en 1820, le physicien danois Ørsted avait découvert qu'un courant peut pertuber fortement le fonctionnement d'un boussole : les courants génèrent des champs magnétiques. En fait, ils sont les sources du champ magnétique, de la même manière que les charges sont les sources du champ électrique.
En présence d'un courant suffisamment intense, l'aiguille aimantée ne pointe plus vers le nord. Elle s'oriente plutôt dans la direction de la tangente à un cercle qui (Fig. 1a) : a) est centré sur le fil électrique (en orange), b) appartient à un plan perpendiculaire au fil et c) passe par le centre de l'aiguille.
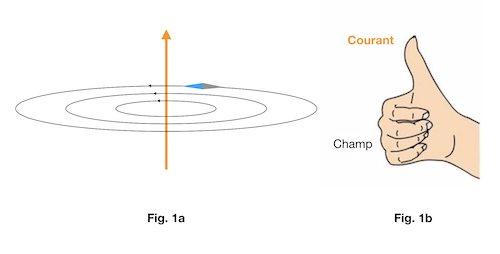
Champ magnétique généré par un courant rectligne
L'orientation de l'aiguille suit les lignes de force du champs magnétique, qui ont une forme circulaire (Fig. 1a, cercles noirs) dans le cas du champ magnétique généré par un fil électrique rectiligne. La direction du champ magnétique est déterminée par la règle de la main droite (Fig. 1b). Si le pouce pointe dans la direction du courant, les autres quatre doigts montrent la direction des lignes de force du champs magnétique.
L'intensité du champs magnétique B à une distance r du fil vaut 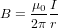 (loi de Biot-Savart), où I est l'intensité du courant dans le fil et
(loi de Biot-Savart), où I est l'intensité du courant dans le fil et 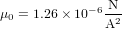 est une constante fondamentale, appelée perméabilité magnétique du vide. Son rôle dans le magnétisme équivaut à celui de la constante de Coulomb dans l'électricité. Les charges sont les sources du champ électrique. Les courants sont les sources du champs magnétique. La constante de Coulomb donne l'intensité du champ électrique par unité de quantité de charge. La perméabilité magnétique du vide donne l'intensité du champ magnétique par unité d'intensité de courant (newton [N] et ampère [A] sont les unités, respectivement, de force et de courant dans le Système International).
est une constante fondamentale, appelée perméabilité magnétique du vide. Son rôle dans le magnétisme équivaut à celui de la constante de Coulomb dans l'électricité. Les charges sont les sources du champ électrique. Les courants sont les sources du champs magnétique. La constante de Coulomb donne l'intensité du champ électrique par unité de quantité de charge. La perméabilité magnétique du vide donne l'intensité du champ magnétique par unité d'intensité de courant (newton [N] et ampère [A] sont les unités, respectivement, de force et de courant dans le Système International).
Champ magnétique généré par un courant circulaire
Le cas d'un circuit circulaire (Fig. 2a) est un peu plus compliqué, mais un cercle peut toujours être décomposé en une infinité de petits morceaux (segments) rectilignes (huit parmi eux ont été mis en évidence en utilisant une couleur cuivre plus foncée). Chaque segment du fil électrique génère un champ magnétique circulaire autour de lui. Les lignes de force de ce champ magnétique sont montrées par les cercles noirs en Fig. 2a. Leur orientation est déterminées par la règle de la main droite.
La somme de tous les champs magnétiques individuels produits par chaque morceau de fil donne le champ magnétique total de l'anneau (la Fig. 2b montre les lignes de force du champ magnétique résultant).
Champ magnétique d'un aimant. Observation expérimentale des lignes de force
Dans le cas d’un aimant, les lignes de force du champ magnétique peuvent être visualisées expérimentalement en déposant l’aimant sur une surface qui a été saupoudrée de limaille de fer. Les parcelles de fer s’alignent aussitôt avec le champ magnétique (Fig. 3).
Analogie avec le champ magnétique d'une bobine
Le champ magnétique généré par l'aimant en Fig. 3 a la même forme que le champ magnétique généré par une bobine, dans laquelle le fil électrique est enroulé sur un support cylindrique (Fig. 4-a ; un courant doit circuler dans la bobine afin qu'il y ait un champ magnétique).
Cette similarité n'est pas fortuite. Le champ magnétique de l'aimant est dû à des courants microscopiques, dont l'effet résultant équivaut à des courants circulaires tout au long de l'aimant (Fig. 4-b ).
Aujourd’hui, nous savons que le magnétisme est un phénomène relativiste, même si, historiquement, l’électricité et le magnétisme ont été découverts d’abord, et c’est en fait à partir de l’électromagnétisme que l’on a découvert la relativité.
Un fil qui se déplace à une vitesse proche de la vitesse de la lumière nous paraîtra plus court que sa longueur propre, à cause de la contraction des longueurs. De la même manière, des particules chargées ayant une vitesse non nulle par rapport à un observateur lui paraîtront être distribuées sur une longueur de fil plus courte, et donc avoir une densité de charge plus élevée que des particules au repos. La vitesse à laquelle les électrons se déplacent dans un fil de cuivre est de l’ordre du millimètre par seconde, elle est donc plus proche de la vitesse de la limace que de celle de la lumière. Mais l’intensité des forces électriques est telle que même une différence minuscule entre la densité de charges positives et la densité de charges négatives perçues par une charge d’essai suffit à produire des effets mesurables, c’est-à-dire, les phénomènes magnétiques.
De la magnétostatique à la magnétodynamique
Un courant est stationnaire si son intensité ne varie pas avec le temps. Si le courant qui génère un champ magnétique est stationnaire, alors le champ magnétique qu’il génère est statique (ses lignes de force ne bougent pas).
Un champ magnétique statique ne génère pas de courant : un aimant posé à côté d'une bobine ne fait pas passer de courant dans la bobine. Mais qu’est-ce qui se passe dans le cas d’un champ magnétique qui varie avec le temps ?
La découverte de l'induction magnétique
Pour répondre à cette question, Michael Faraday fit une expérience dans laquelle le fil électrique marqué a dans la Fig. 1 était enroulé autour d’un côté d'un anneau de cuivre. Lorsque les extrémités du fil étaient connectées aux pôles d’une pile, le courant qui passait dans la bobine générait un champs magnétique B dans l’anneau. Les cercles rouges en Fig. 1 montrent ses lignes de forces.
Après avoir coupé le courant, il enroula un deuxième fil électrique marqué b autour de l’autre côté de l’anneau et il relia ces extrémités à un galvanomètre c, un instrument qui mesure l’intensité du courant qui passe dans le circuit. Chaque fois qu’il connectait ou qu'il déconnectait les extrémité du fil a à la pile, le galvanomètre détectait le passage d’un courant transitoire dans le fil b. La variation soudaine du champs magnétique à l’intérieur de la bobine b, fusse-t-elle sous forme d'apparition ou de disparition, générait une force électrique (la force électromotrice) qui mettait les charges en mouvement et donc causait le passage d’un courant dans la circuit b.
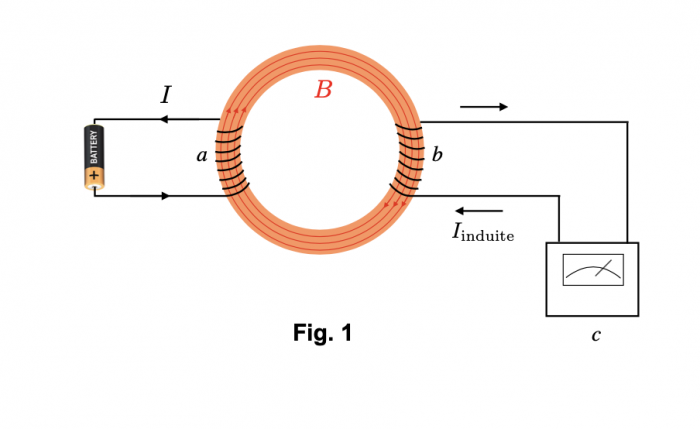
On pourrait imaginer que c’est le cuivre qui transporte la force électromagnétique et que, sans l’anneau de cuivre, le courant dans le circuit a n’aurait aucun impact sur ce qui se passe dans le circuit b. Une autre expérience, toujours par Faraday, dément cette hypothèse. Dans la deuxième expérience (Fig. 2), les bobines était enroulées sur des cylindres creux. Les circuits a et b étaient complètement déconnectés. Pourtant, le résultat ne changeait pas. Chaque fois que Faraday fermait ou ouvrait le circuit a, le galvanomètre mesurait un courant transitoire dans le circuit b.
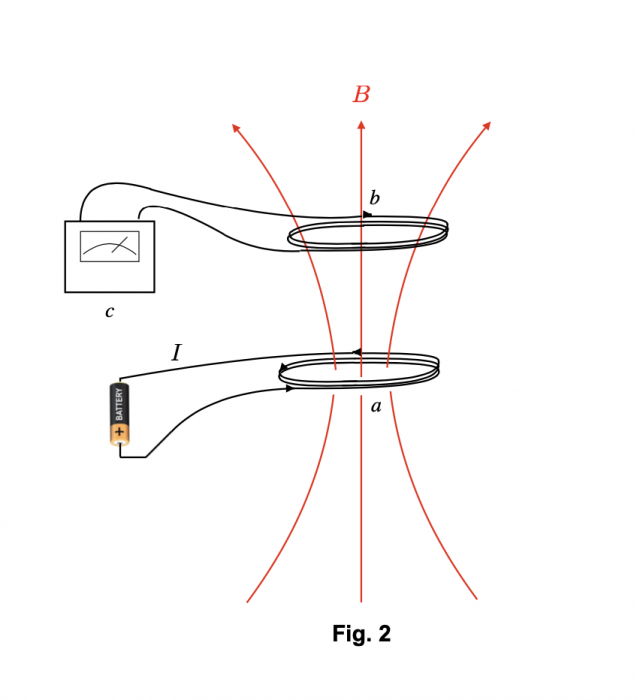
Faraday fit aussi l’expérience de rapprocher et éloigner la bobine a de la bobine b lorsque les extrémités du fil a étaient connectées à la pile et un courant stationnaire circulait dans le circuit. Quand la bobine a était plus proche, le champs magnétique à l’intérieur de la bobine b était plus intense. Quand elle était plus lointaine, il devenait plus faible. Les variations du champ magnétique était détectées par des mouvements soudains de l’aiguille du galvanomètre.
Le champ magnétique comme entité physique
Faraday refusait la notion d’une action à distance d’un circuit sur l'autre. En même temps, c’était évident que ce n’était pas le cuivre qui transportait la force, parce que le phénomène se produisait aussi bien dans l’air, qui a des propriétés électriques complètement différentes de celles du cuivre. L'explication de Faraday était que l’interaction se passait à travers la médiation du champ magnétique lui même, que Faraday voyait comme une entité physique et non pas comme un simple concept mathématique pour décrire une force dont l’intensité dépend de la position.
Le courant qui s’instaure dans la bobine connectée à la batterie génère un champ magnétique, qui monte en intensité et se propage dans l'espace jusqu'à l’intérieur de l’autre bobine, avec l’effet d’y induire un courant (voici pourquoi on appelle ce phénomène induction électromagnétique). Quand le champ magnétique généré par le courant dans la bobine b atteint sa valeur finale, il devient statique. A ce point-là, l'« onde d’électricité » disparaît comme une vague de tsunami après son passage dévastateur et le courant dans le circuit de la batterie cesse d'avoir aucun effet sur le circuit du galvanomètre.
L’explication proposée par Faraday fut reçue avec scepticisme par ses contemporains. Non seulement la notion de lignes de force y était introduite pour la première fois et sans formalisation mathématique rigoureuse, mais aussi Faraday était le premier voir le champ magnétique non pas comme une abstraction mathématique, mais comme une entité physique qui remplissait l’espace, se propageait dans l’espace et transportait une force.
Un champ magnétique variable génère un champ électrique
James Clerk Maxwell fut un des premiers physiciens à embrasser l'idée révolutionnaire du champs comme entité physique. Maxwell savait qu'une charge au repos ne peut se mettre en mouvement que sous l’effet d’un champ électrique (cela découle du principe d'inertie : un corps au repos ne peut se mettre en mouvement que sous l'action d'une force). Il compris donc que, pour induire un courant, la variation du champ magnétique doit générer un champ électrique.
Le point fondamental de cet argument est que la relation est entre les deux champs, et non pas entre un circuit et l'autre. La variation du champ magnétique génère un champ électrique indépendamment du fait qu’il y ait des charges électriques ou des dispositifs expérimentaux susceptibles d’être influencés par l'action de ce dernier (dans l’expérience de Faraday, la bobine connectée au galvanomètre). On pourrait faire une analogie avec la pluie, qui tombe de la même manière si nous sommes déjà rentrés chez nous ou si nous sommes encore en chemin sans parapluie.
La conséquence ultime de ce raisonnement est que l'induction (la génération d'un champ électrique par un champ magnétique variable) ne nécessite pas de la présence de matière ni de courant. Elle peut se passer ainsi bien dans le vide.
Un champ électrique variable génère un champ magnétique
Plus tard, Maxwell découvrit que, de la même manière qu’un champ magnétique variable génère un champ électrique, la cohérence logique de son système d’équations pour les champs électriques et magnétiques impose qu’un champ électrique variable génère un champ magnétique.
Les équations de Maxwell montrent que l'électricité et le magnétisme ne sont que deux manifestations d'une seule réalité fondamentale : le champ électromagnétique.
Ondes électromagnétiques
Avec la découverte qu'un champ électrique variable génère un champ magnétique, Maxwell avait trouvé un mécanisme qui permettait aux forces électriques et magnétiques de se propager à distance, tout en préservant la localité de l’interaction électromagnétique. Un champ électrique génère un champ magnétique, qui génère un champ électrique, qui génère un champ magnétique, et caetera. De cette manière, une perturbation dans le champ électromagnétique se propage comme une onde d’un point de l’espace à un autre proche de lui, jusqu’à couvrir des distances parfois aussi grandes que la taille de l’Univers.
La figure ci-dessus montre le champ électrique 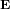 et le champ magnétique
et le champ magnétique 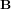 dans une onde électromagnétique qui se propage dans la direction de l'axe x. Le champ électrique (en bleu) vibre dans le plan xy. Le champ magnétique (en rouge) vibre dans le plan xz.
dans une onde électromagnétique qui se propage dans la direction de l'axe x. Le champ électrique (en bleu) vibre dans le plan xy. Le champ magnétique (en rouge) vibre dans le plan xz.  est la longueur d'onde.
est la longueur d'onde.
La lumière est une onde électromagnétique
La vitesse c à laquelle les ondes électromagnétiques se propagent est déterminée par la constante de Coulomb et la perméabilité magnétique du vide à travers la formule 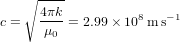 .
.
La vitesse c calculée ci-dessus coïncide avec la vitesse de la lumière, que Rømer avait mésuré en 1676 par l'observation astronomique. L'égalité entre la vitesse des ondes électromagnétiques et la vitesse de la lumière prouve que la lumière visible n’est qu’un cas particulier d'ondes électromagnétique. Elle correspond aux ondes électromagnétiques avec des longueurs comprises entre 0.4 et 0.7 micromètres.
Le champs transporte de l'énergie et propage l'interaction électromagnétique
Nous sommes donc partis de la vision de Coulomb, qui raisonnait en terme d’action à distance, pensée comme instantanée, pour aboutir à une nouvelle vision, dans laquelle le champ électromagnétique est une entité physique réelle, qui contient et transporte de l’énergie. Transporter de l'énergie équivaut à transporter de la matière, étant donnée l’équation d’Einstein 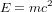 . Les particules qui composent le champ électromagnétique – les photons – n’ont pas de masse, alors que les protons, les neutrons et les électrons en ont une, mais cela ne rend pas la lumière moins physiquement réelle qu’une pomme.
. Les particules qui composent le champ électromagnétique – les photons – n’ont pas de masse, alors que les protons, les neutrons et les électrons en ont une, mais cela ne rend pas la lumière moins physiquement réelle qu’une pomme.
C’est par la médiation du champ électromagnétique que l’interaction électromagnétique se propage, et cette propagation se fait à une vitesse finie, même si elle est très élevée. Donc la force qu’une charge exerce sur une autre par la médiation du champ n’est pas instantanée. Elle agit avec un délai égal au temps que la lumière prend pour aller d’une charge à l’autre. Ce pourrait-il que ceci soit vrai aussi pour la force gravitationnelle ?
Vitesse relative, accélération absolue
Dans la mécanique newtonienne, la vitesse est relative – elle dépend du référentiel, – mais l’accélération (la variation de vitesse) est absolue. Ce concept est illustré par l'exemple d'un voyageur sur un train. Nous considérerons deux cas. Dans le premier, le train roule à une vitesse constante. Dans le deuxième, il accélère (ou décélère) brusquement.
Quand le train voyage à une vitesse constante, s'il n'y a pas de roulis, le mouvement du train est imperceptible. Le passager prend son petit déjeuner confortablement assis dans son siège, comme s'il était chez lui (Fig. 1a). Seulement en voyant les arbres à côté du chemin de fer venir vers lui, le passager s'aperçoit que le train est mouvement. Dans un tunnel, avec tous les rideaux fermés, il pourrait bien se demander, à un certain moment, si le train roule ou s'il est à l'arrêt. Il est impossible pour le passager de déterminer la vitesse du train sans regarder hors des fenêtres. La vitesse du train n'est définie que par rapport à quelque chose d'externe au train.
En revanche, si le train ralentit brusquement (ce qui correspond à une accélération négative), le passager s'en aperçoit tout de suite, parce qu'il voit son café et son jus d'orange partir en avant (Fig. 1b). Les dégâts que le café et le jus d'orange produisent s'ils se renversent sur le costume ou l'ordinateur du passager constituent des faits objectifs. La décélération brutale du train est une réalité absolue. Elle ne dépend pas du référentiel utilisé pour décrire le mouvement.
L'inertie et les forces apparentes
La réalité indéniable que les verres avec le café et le jus d'orange se sont renversés n'explique pas quelle force a provoqué cet accident. Chercher cette force est, pourtant, inutile, parce qu'elle n'existe pas. Tout simplement, les verres voyageaient avec la même vitesse que le train. Quand le train a ralenti, ils ont continué à avancer à la même vitesse. Si un verre avance plus vite que la tablette sur laquelle il a été posé, c'est logique qu'il puisse se renverser. Ce qui pourrait paraître comme une force est donc la tendance du mouvement acquis à se conserver en l’absence de forces contraires. Cette tendance est dite inertie.
On peut, bien sûr, décrire les effets de l'inertie come les conséquences d'une force si, selon la logique des apparences, on cherche à décrire les phénomènes comme ils se présentent à la personne qui les observe (phenomena est le mot grec pour apparences). On dit, alors, que l'inertie se manifeste comme une force apparente dans le référentiel de l'observateur.
Derrière cette force apparente, il y a une force une force réelle : c'est la force de freinage, qui cause la décélération du train. L'observateur a l'impression qu'une force agit sur les verres, alors qu'en réalité la force agit sur lui et sur le wagon dans lequel il se trouve.
Le principe d'équivalence
L’accélération gravitationnelle présente une particularité. Le principe fondamental de la dynamique nous dit que l’action d’une force F sur un corps de masse m produit une accélération 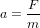 . Dans le cas de l'électricité, la force F avec laquelle deux charges s'attirent ne dépend de leurs masses (les masses apparaissent nulle part dans la loi de Coulomb). Donc, l’accélération a sera plus grande pour un corps moins massif et plus petite pour un corps plus massif.
. Dans le cas de l'électricité, la force F avec laquelle deux charges s'attirent ne dépend de leurs masses (les masses apparaissent nulle part dans la loi de Coulomb). Donc, l’accélération a sera plus grande pour un corps moins massif et plus petite pour un corps plus massif.
Dans le cas de la gravitation, la force F avec laquelle deux masses M et m s'attirent est 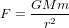 , où r est la distance entre les deux masses et G est la constante de gravitation universelle. Donc, l'accélération de la masse m due à l'attraction gravitationnelle de la masse M,
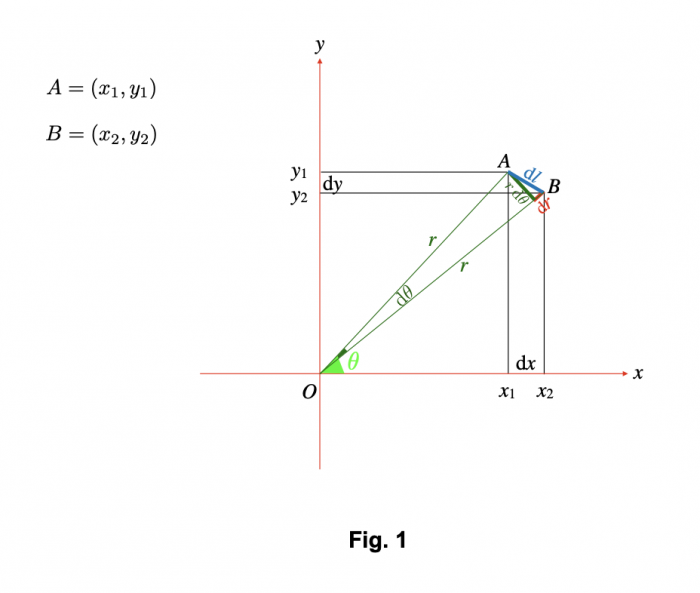
, où r est la distance entre les deux masses et G est la constante de gravitation universelle. Donc, l'accélération de la masse m due à l'attraction gravitationnelle de la masse M, 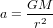 , ne dépend pas de m. L'accélération gravitationnelle est la même pour un pomme de 200 g et une balle de canon de 5 kg. Si on laisse chuter un pomme de 200 g et une balle de canon de 5 kg de la même hauteur, elles arriveront au sol en même temps, si on néglige la résistance de l'air.
, ne dépend pas de m. L'accélération gravitationnelle est la même pour un pomme de 200 g et une balle de canon de 5 kg. Si on laisse chuter un pomme de 200 g et une balle de canon de 5 kg de la même hauteur, elles arriveront au sol en même temps, si on néglige la résistance de l'air.
Par conséquent, un observateur en chute libre (un observateur qui se jette par la fenêtre en même temps qu'il jette la pomme) ne devrait mesurer aucune accélération, parce que le corps (la pomme) dont il essaie de mesurer l'accélération chute toujours à la même vitesse que lui. On appelle ceci le principe d’équivalence.
Dans l'ascenseur
gauche : Figure 2a. Droite : Figure 2b
Crédit :
S. Cnudde
Cette conclusion pourrait paraître paradoxale. Imaginons que je suis dans un ascenseur. La raison on la comprendra plus tard. J’ai une pomme dans ma main, je la lâche, je vois bien qu’elle chute par terre (Fig 2a). Pourtant, dans ce cas-ci, le principe d’équivalence est mal appliqué parce que la pomme est en chute libre (si on néglige la résistance de l’air), alors que l’observateur a les pieds au sol. La résistance du sol agit sur lui et l'empêche de s’y enfoncer. Imaginez de refaire l’expérience dans un ascenseur au dernier étage et que le câble qui retient l’ascenseur se coupe juste avant que vous ne lâchiez la pomme (Fig. 2b). Alors, vous ne verrez pas la pomme chuter, parce que vous chuterez à la même vitesse qu’elle. Votre expérience (avant que vous vous écrasiez au sol quand l’ascenseur arrive au rez-de-chaussée) sera égale à celle que vous auriez faite si l’ascenseur avait été transporté dans l’espace et que vous étiez dans une situation d’apesanteur, c'est-à-dire d'absence de gravité.
Implications pour la nature de la gravité
Newton avait compris l’existence du principe d’équivalence, mais il n’avait pas su l’expliquer. Einstein réfléchit à l’expérience de l’ascenseur et il nota l'analogie avec le passager sur le train. Dans le train, la force apparente est absente quand le wagon roule par inertie, elle se manifeste quand une force réelle en modifie le mouvement. Dans l'ascenseur, la force de gravité est indétectable quand il est en chute libre, elle se manifeste quand une force agit sur l'ascenseur (la tension des cables qui retient la cabine).
Dans le train

Crédit :
S. Cnudde
Einstein en conclut que la gravité est une force apparente, qui se manifeste quand on utilise un référentiel qui n'est pas en chute libre et l'on se met du point de vue d'un observateur sujet à d'autres forces d'origine non-gravitationnelle
Mouvements et observateurs inertiels
Un mouvement est purement inertiel quand le corps qui se déplace n'est sujet à aucune force réelle. Un observateur inertiel est un observateur qui ne se déplace que par inertie. Dans le référentiel d'un tel observateur, il n'y a pas de forces apparentes.
En mécanique newtonienne, le principe d'inertie affirme que tout corps persévère dans son état de repos ou de mouvement uniforme en ligne droite, à moins qu'il ne soit contraint, par des forces s'imprimant sur lui, à changer cet état. Le mouvement inertiel étant rectiligne, il coïncide forcement avec le chemin le plus court entre deux points, dit aussi le chemin géodésique. La notion que le mouvement inertiel correspond au chemin géodésique continue à valoir dans la théorie de la relativité d'Einstein.
Einstein a, cependant, une notion de référentiel inertiel beaucoup plus étendue que Newton. Pour Newton, un observateur inertiel est un observateur sur lequel aucune force externe n’agit, donc un observateur isolé. Pour Einstein, un observateur inertiel est un observateur en chute libre, dans la mesure où il ne considère pas la gravité comme une force.
Deux visions de la géométrie
A la base de cette différence, il y a une perception différente de la géométrie. La géométrie est la description mathématique de l’espace. Pour Newton, la géométrie pré-existe à la physique. Que l’espace contienne de la matière ou qu’il soit vide ne change rien dans sa géométrie. Pour Einstein, l’espace n’est pas obligé d’obéir à la géométrie d’Euclide. C’est la matière qui, par sa distribution dans l’espace, en crée la géométrie.
La matière courbe le chemin géodésique
On peut comprendre la théorie d’Einstein en visualisant l’espace comme la surface d’un matelas, en deux dimensions, que nous supposons être plate quand personne ne s'assoit ou s'étend dessus. Si nous lançons une bille (représentée en rouge dans la figure en bas) sur un matelas quand celui-ci est vide, en absence de forces qui en perturbent le mouvement, la bille se déplacera sur la surface du matelas en empruntant le chemin le plus court – une ligne droite où la surface du matelas est plate (le chemin ACB pour aller de A à B en Fig. 1a). Si nous répétons l’expérience après avoir déposé sur le matelas une balle de bowling (la grosse sphère noire), alors la bille déviera dans la direction de la dépression créée dans le matelas par la balle de bowling et pourra même tomber dessus si sa vitesse n’est pas suffisamment grande (Fig. 2b). Le chemin géodésique pour aller de A à B sur la surface courbe ne passe plus par C.
Dans notre espace, en trois dimensions, un corps massif – la Terre, le Soleil ou un trou noir, – agit comme la balle de bowling. Il courbe localement la géométrie de l’espace, d’une manière que le chemin géodésique cesse d’être une ligne droite (nous avons mis en évidence le mot localement parce que la balle de bowling courbe le chemin entre A et B, elle ne courbe pas le chemin entre D et E).
Pensez à un vol Paris - Sidney. Le chemin le plus court parmi tous les parcours possibles est celui qui correspond à un grand cercle entre le point de départ et le point d’arrivée. Une droite n’est pas une option parce que le mouvement est obligé de suivre la surface bidimensionnelle de la Terre, qui est courbe (l’avion ne peut pas creuser un tunnel par le centre de la planète). Dans le cas de la théorie de la relativité générale d’Einstein, c’est l’espace tridimensionnel qui est courbe. La contrainte vient donc du fait que l’on est obligé de se déplacer dans l’espace, il n’est pas possible de se déplacer autrement.
Dans les images utilisées ci-dessus, du matelas ou des parcours en avion, l'espace considèré est en deux dimensions (surface du matelas ou surface de la Terre), alors que notre espace est en trois dimensions (longueur, largeur, hauteur), mais, dans le cas de la théorie de la relativité générale d’Einstein, c’est l’espace tridimensionnel qui est courbe.
Définition
Nous avons écrit que la présence de matière modifie la géométrie de l'espace. En fait, la propriété modifiée est la métrique, c'est-à-dire la loi qui donne la distance entre deux points.
La métrique euclidienne
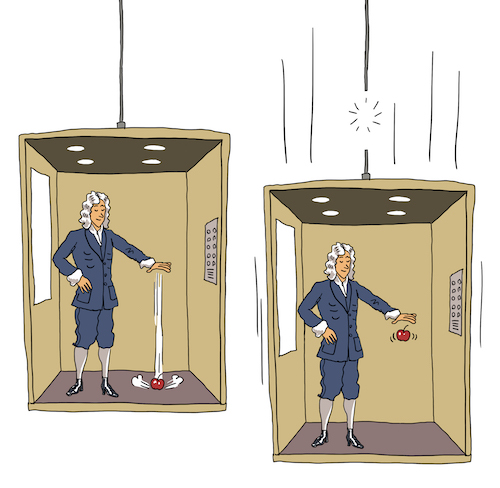
Commencons par le cas simple de deux points A et B de coordonnées 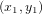 et
et 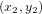 , respectivement sur le plan cartésien (Fig. 1). La distance dl entre les deux points est donnée par le théorème de Pythagore :
, respectivement sur le plan cartésien (Fig. 1). La distance dl entre les deux points est donnée par le théorème de Pythagore :
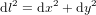 (1),
(1),
où 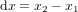 et
et 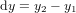 .
.
Nous pouvons généraliser l'équation (1) au cas de deux points 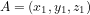 et
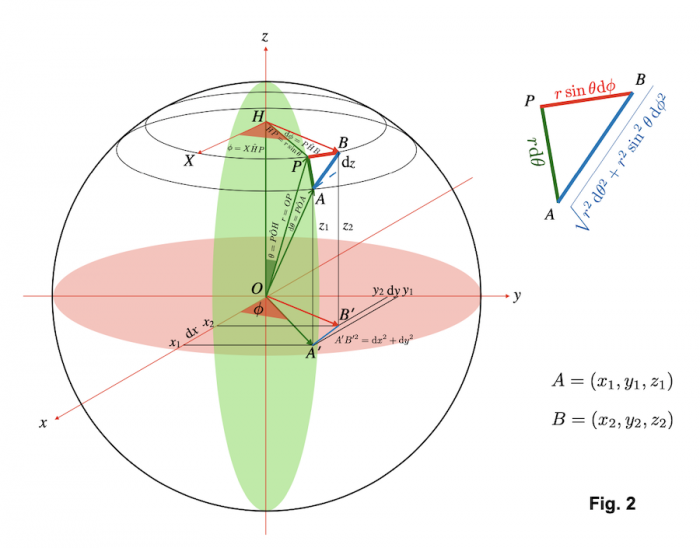
et 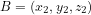 dans l'espace en trois dimensions. En appliquant deux fois le théorème de Pythagore (Fig. 2), nous trouvons :
dans l'espace en trois dimensions. En appliquant deux fois le théorème de Pythagore (Fig. 2), nous trouvons :
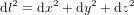 (2).
(2).
Les équations (1) et (2) expriment la métrique euclienne, respectivement en deux et trois dimensions. La métrique euclidienne est la loi qui permet de calculer la distance dl entre deux points quelconques dans la géométrie d'Euclide.
Les équations (1) et (2) sont formulées en coordonnées cartésiennes orthogonales. On aurait pu considérer d'autres systèmes de coordonnées, par exemple, en deux dimensions, les coordonnées polaires. En coordonnées polaires (Fig. 2), un point A est identifié par deux coordonnées : la distance r de l'origine O et l'angle  que la droite OA forme avec une droite de référence (en Fig. 1, l'axe x). Dans ce système de coordonnées, la distance
que la droite OA forme avec une droite de référence (en Fig. 1, l'axe x). Dans ce système de coordonnées, la distance 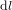 entre les points
entre les points 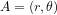 et
et 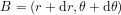 est déterminée par l'équation :
est déterminée par l'équation :
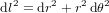 (3),
(3),
qui exprime, encore une fois, le théorème de Pythagore, cette fois en coordonnées polaires (on note qu’en Fig.1 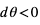 ).
).
Cépendant, un changement de coordonnées n'est pas un changement de métrique. Les équations (1) et (3) ont des formes différentes, mais elles correspondent à la même métrique parce qu'elles donnent le même résultat pour la distance 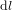 entre deux points*. Un changement de métrique est – nous le verrons bientôt – quelque chose de plus profond.
entre deux points*. Un changement de métrique est – nous le verrons bientôt – quelque chose de plus profond.
*Affirmer que les équations (1) et (3) donnent le même résultat pour la longeuer 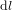 est correct dans la limite que
est correct dans la limite que 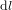 est infinitésimale. Autrement, on ne peut pas traiter l'arc de cercle de longueur
est infinitésimale. Autrement, on ne peut pas traiter l'arc de cercle de longueur 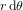 comme un segment et l'on ne peut pas supposer qu'il soit perpendiculaire au segment de longueur
comme un segment et l'on ne peut pas supposer qu'il soit perpendiculaire au segment de longueur 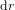 .
.
La métrique sur une sphère
Pour comprendre comment la métrique peut différer de celle d'Euclide, considérons la géométrie sur une surface sphérique (par exemple, le globe terrestre; Fig. 2).
Un lieu sur la surface de la sphère est identifié par deux coordonnées : la co-latitude*  et la longitude
et la longitude 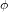 , étant donné que la distance r du centre de la Terre est la même pour tous les points. A
, étant donné que la distance r du centre de la Terre est la même pour tous les points. A 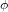 , constante, une variation infinitésimale
, constante, une variation infinitésimale 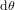 de la latitude correspond à un déplacement de
de la latitude correspond à un déplacement de 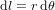 , si les angles sont exprimés en radians. A
, si les angles sont exprimés en radians. A  constante, une variation infinitésimale
constante, une variation infinitésimale 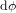 de la longitude correspond à un déplacement de
de la longitude correspond à un déplacement de 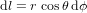 . Dans la limite où des arcs infinitésimaux peuvent être considérés comme rectilignes, le théorème de Pythagore donne :
. Dans la limite où des arcs infinitésimaux peuvent être considérés comme rectilignes, le théorème de Pythagore donne :
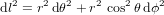 (4).
(4).
L'équation (4) est fondamentalement différente des équations (1) et (3). Les équations (1) et (3) donnent la distance entre deux points sur le plan, donc une surface plate. L'équation (4) donne l'élément infinitésimal de distance sur une sphère, donc une surface courbe.
Pour mieux comprendre cette différence, considérons la distance l entre le pôle Nord et le pôle Sud de la Terre : l est le diamètre terrestre si on voit les pôles comme deux points dans l'espace en trois dimensions et le méridien terrestre si on voit les pôles comme deux points sur la surface terrestre. La métrique (2) correspond au premier cas, 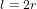 . La métrique (4) correspond au deuxième cas,
. La métrique (4) correspond au deuxième cas, 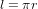 . La métrique (4) est non-euclidienne parce qu'elle mesure les distances sur une surface courbe.
. La métrique (4) est non-euclidienne parce qu'elle mesure les distances sur une surface courbe.
Pour résumer, l'équation (1) donne la métrique sur une surface plate. L'équation (2) donne la métrique dans un espace plat (en espace qui obéit à la géométrie d'Euclide).
La notion de distance sur une surface peut être généralisée à des surfaces courbes. C'est comme ça que l'on passe de la métrique (1) à la métrique (4).
De la même manière, la notion de distance dans l'espace en trois dimensions (équation 2) peut être généralisée à des espaces courbes, qui correspondent à des métriques plus complexes et n'obéissant pas à la géométrie d'Euclide.
* : La latitude utilisée en géographie est l’angle avec le plan équatorial. Elle est nulle à l’équateur. En géométrie et en physique, on utilise plutôt la co-latitude, qui est l’angle avec l’axe polaire. Elle est nulle au pôle nord.
La quatrième dimension
L'équation (6) vous semble complexe ? Les métriques utilisées dans la théorie de la relativité d’Einstein le sont encore plus, parce qu'elles considérent non seulement l'espace, mais aussi l’espace-temps. Dans la théorie de la relativité, c’est le mouvement dans l’espace-temps et non pas le mouvement purement spatial qui nous intéresse.
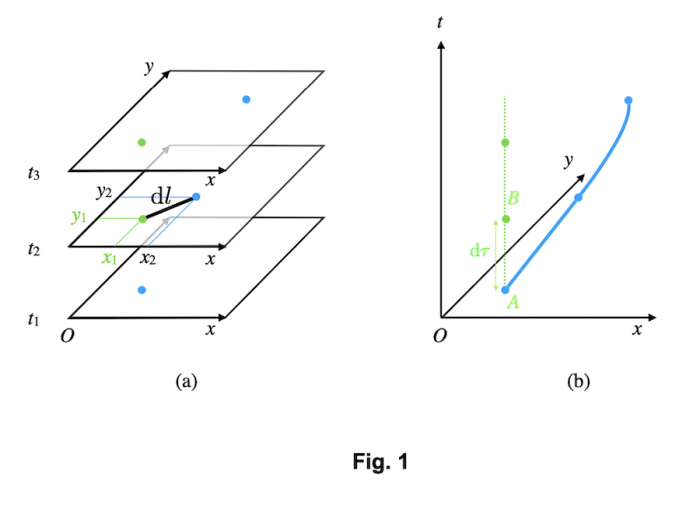
Pour comprendre ce qu’est l’espace-temps, considérons un corps – par exemple, une boule de billard – qui se déplace sur une surface. Vous pouvez imaginer son mouvement comme une série de photographies instantanées qui montrent sa position (Fig. 1a, cercles bleus pleins) aux temps 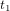 ,
, 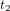 ,
, 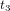 , etc. Imaginez maintenant d’empiler toutes ces photographies instantanées et de tracer une courbe qui connecte les positions du corps dans toutes les photographies instantanées empilées (Fig 1b, courbe bleue continue). Voici la trajectoire du corps dans l’espace-temps. En relativité, on appelle cette trajectoire une ligne d'univers.
, etc. Imaginez maintenant d’empiler toutes ces photographies instantanées et de tracer une courbe qui connecte les positions du corps dans toutes les photographies instantanées empilées (Fig 1b, courbe bleue continue). Voici la trajectoire du corps dans l’espace-temps. En relativité, on appelle cette trajectoire une ligne d'univers.
La Fig. 1b montre une image en trois dimensions (deux dimension spatiales et une dimension temporelle) parce que nous ne nous pouvons pas visualiser une image en quatre dimensions. L'espace-temps réel a quatre dimensions parce l'espace en a trois (les corps ne sont pas contraints à se déplacer sur une surface).
Le temps propre
Soit 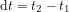 , que nous considérons comme un intervalle de temps infinitésimal, et soient dx, dy, dz les variations entre
, que nous considérons comme un intervalle de temps infinitésimal, et soient dx, dy, dz les variations entre 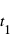 et
et 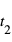 des coordonnées spatiales du corps représenté par le cercle bleu en Fig. 1.
des coordonnées spatiales du corps représenté par le cercle bleu en Fig. 1.
La distance dl parcourue par le corps dans l'intervalle de temps dt est donnée par 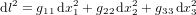 , qui se réduit à
, qui se réduit à 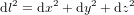 pour la métrique euclidienne en coordonnées cartésiennes. En Fig. 1, les cercles verts montrent la position initiale du corps ; d
pour la métrique euclidienne en coordonnées cartésiennes. En Fig. 1, les cercles verts montrent la position initiale du corps ; d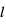 est le déplacement par rapport à la position initiale.
est le déplacement par rapport à la position initiale.
La ligne verte pointillée (Fig. 1b) est la ligne d'univers pour un corps au repos, pour lequel 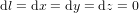 . Pour ce corps, le seul changement est le temps
. Pour ce corps, le seul changement est le temps 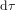 qui s'écoule entre les évènements* A et B. Ce temps-ci est appelé temps propre, parce que c’est le temps dans le référentiel du corps (le référentiel dans lequel le corps est au repos). Le temps propre est indiqué avec la lettre grecque
qui s'écoule entre les évènements* A et B. Ce temps-ci est appelé temps propre, parce que c’est le temps dans le référentiel du corps (le référentiel dans lequel le corps est au repos). Le temps propre est indiqué avec la lettre grecque  pour le distinguer du temps t dans le référentiel de l'observateur . La théorie de la relativité s'appelle comme ça parce que le temps n'est pas absolu. Son écoulement dépend de l'observateur qui le mesure.
pour le distinguer du temps t dans le référentiel de l'observateur . La théorie de la relativité s'appelle comme ça parce que le temps n'est pas absolu. Son écoulement dépend de l'observateur qui le mesure.
Dans le référentiel dans lequel un corps est au repos, 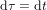 par définition, mais comment mettre en relation le temps propre
par définition, mais comment mettre en relation le temps propre  mesuré par un astronaute qui voyage dans un vaisseau spatial avec le temps t mésuré par un observateur externe, pour lequel l'astronaute se déplace à grande vitesse ? Les transformations de Lorentz répondent à cette question.
mesuré par un astronaute qui voyage dans un vaisseau spatial avec le temps t mésuré par un observateur externe, pour lequel l'astronaute se déplace à grande vitesse ? Les transformations de Lorentz répondent à cette question.
* : *En relativité, un événement est la présence d’un corps dans un point de l’espace à un temps donné (la présence de Telleyrand au Congrès de Vienne en 1815 est un événement).
Les transformations de Lorentz
Considérons un astronef qui part de la planète O et qui voyage à vitesse v constante dans la direction de l'axe x. La planète O se situe à 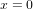 . L'astronaute qui pilote l'astronef et la tour de contrôle sur O ont synchronisé leurs montres à l'instant de départ
. L'astronaute qui pilote l'astronef et la tour de contrôle sur O ont synchronisé leurs montres à l'instant de départ 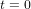 . Pour la tour de contrôle, l'abscisse de l'astronef au temps t est
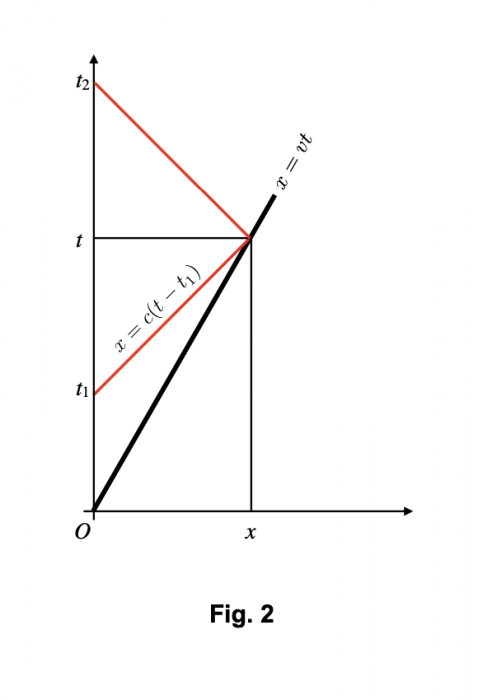
. Pour la tour de contrôle, l'abscisse de l'astronef au temps t est 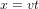 . La ligne droite noire épaisse en Fig. 2 montre la relation entre x et t pour l'astronef dans le référentiel de la tour de contrôle.
. La ligne droite noire épaisse en Fig. 2 montre la relation entre x et t pour l'astronef dans le référentiel de la tour de contrôle.
Au temps 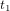 dans son référentiel, la tour de contrôle envoie un message radio à l'astronaute. Le message radio se propage à la vitesse de la lumière (les ondes radio sont des ondes électromagnétiques), donc il va plus vite que l'astronef, même s'il part plus tard. Au temps
dans son référentiel, la tour de contrôle envoie un message radio à l'astronaute. Le message radio se propage à la vitesse de la lumière (les ondes radio sont des ondes électromagnétiques), donc il va plus vite que l'astronef, même s'il part plus tard. Au temps 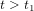 , le message radio a parcouru une distance
, le message radio a parcouru une distance 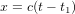 (cette équation correspond à la ligne rouge continue). Quand le message parvient à l'atronaute, l'astronaute répond tout de suite. Les traits rouges montrent la ligne d'univers du message de réponse. La tour de contrôle reçoit la réponse au temps
(cette équation correspond à la ligne rouge continue). Quand le message parvient à l'atronaute, l'astronaute répond tout de suite. Les traits rouges montrent la ligne d'univers du message de réponse. La tour de contrôle reçoit la réponse au temps 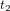 . Nous allons analyser ces événements, d'abord de la perspective de la tour de contrôle, puis de celle de l'astronaute.
. Nous allons analyser ces événements, d'abord de la perspective de la tour de contrôle, puis de celle de l'astronaute.
La Fig. 2 utilise le référentiel de la tour de contrôle. Pour déterminer quand l'astronaute reçoit le message, la tour du contrôle cherche à quel temps t la distance parcourue par le signal radio est égale à celle parcourue par l'astronef. La condition 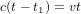 donne
donne 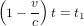 et donc :
et donc :
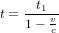 (1).
(1).
Nous avons supposé que l'astronaute répond tout de suite. Donc la distance x entre l'astronef et O est la même quand l'astronaute reçoit le message de la tour et quand il envoie sa réponse. Comme la distance x parcourue par le signal radio est la même dans les deux sens, le temps 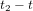 que le message de l'astronaute prend pour parvenir à la tour de contrôle est égal au temps
que le message de l'astronaute prend pour parvenir à la tour de contrôle est égal au temps 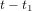 que le message de la tour prend pour parvenir à l'astronaute. La condition
que le message de la tour prend pour parvenir à l'astronaute. La condition 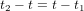 donne :
donne :
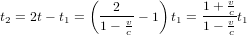 (2).
(2).
Soit  le temps affiché par la montre de l'astronaute quand il reçoit le message de la tour de contrôle. En appliquant le même argument qui amène le personnel de la tour à écrire l'équation (1), l'astronaute conclut que la tour recevra sa réponse au temps :
le temps affiché par la montre de l'astronaute quand il reçoit le message de la tour de contrôle. En appliquant le même argument qui amène le personnel de la tour à écrire l'équation (1), l'astronaute conclut que la tour recevra sa réponse au temps :
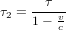 (3)
(3)
La question est quelle est la relation entre les temps  et
et 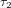 mesurés par l'astronaute et les temps
mesurés par l'astronaute et les temps  et
et 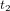 mesurés par la tour. Nous y répondrons en déterminant la valeur du paramètre
mesurés par la tour. Nous y répondrons en déterminant la valeur du paramètre 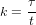 . Notre calcul se base sur un argument de réciprocité. Si le temps
. Notre calcul se base sur un argument de réciprocité. Si le temps  auquel l'astronaute reçoit le message dans son référentiel est k fois le temps t que la tour a calculé dans son référentiel, alors le temps
auquel l'astronaute reçoit le message dans son référentiel est k fois le temps t que la tour a calculé dans son référentiel, alors le temps 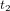 auquel la tour reçoit le message de réponse devra être k fois le temps de réception
auquel la tour reçoit le message de réponse devra être k fois le temps de réception 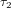 calculé par l'astronaute. Donc :
calculé par l'astronaute. Donc :
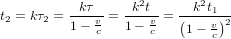 (4),
(4),
où nous avons utilisé (dans l'ordre) l'équation (3), la relation 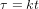 et l'équation (1). Les temps
et l'équation (1). Les temps 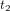 calculés avec l'équation (4) et l'équation (2) doivent être égaux. En posant :
calculés avec l'équation (4) et l'équation (2) doivent être égaux. En posant :
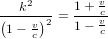 (5)
(5)
on trouve 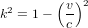 et donc :
et donc :
![\tau^2=\left[1-\left({v\over c}\right)^2\right]t^2](../pages_gravite/equations_gravite-nature/equation96.png) (6).
(6).
Dans le cas limite 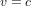 , l'équation (1) donne
, l'équation (1) donne 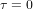 pour n'importe quelle valeur de dt. Pour quelqu'un qui va à la vitesse de la lumière, le temps ne passe pas ! Cela est pourtant impossible pour un corps massif, tel que notre astronef, parce que l'énergie qu'il faudrait pour l'amener à la vitesse de la lumière est infinie. La lumière n'a pas de masse.
pour n'importe quelle valeur de dt. Pour quelqu'un qui va à la vitesse de la lumière, le temps ne passe pas ! Cela est pourtant impossible pour un corps massif, tel que notre astronef, parce que l'énergie qu'il faudrait pour l'amener à la vitesse de la lumière est infinie. La lumière n'a pas de masse.
Notre raisonomment ne contient aucune hypothèse sur la durée du temps t, qui pourrait être très long ou très court. Nous pouvons donc remplacer les temps  et
et  par les temps infinitésimaux
par les temps infinitésimaux 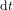 et
et 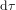 , et réécrire l'équation (6) dans la forme :
, et réécrire l'équation (6) dans la forme :
![{\rm d}\tau^2=\left[1-\left({v\over c}\right)^2\right]{\rm\,d}t^2](../pages_gravite/equations_gravite-nature/equation103.png) (7).
(7).
L'équation (7) est plus générale, parce qu'elle s'applique aussi à des mouvements qui ne sont pas rectilignes uniformes. Même si la vitesse v de l'astronef change avec le temps, elle peut toujours être considérée constante dans des intervalles de temps infinitésimaux. L'équation (7) est connue comme la transformation de Lorentz pour le temps (il y en a une deuxième pour les longueurs).
La vitesse est le déplacement par unité de temps :
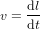 (8).
(8).
En replaçant la vitesse v donnée par l'équation (8) dans l'équation (7), nous trouvons l'expression finale pour le temps propre :
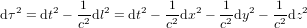 (9),
(9),
qui sera à la base de la discussion qui suit.
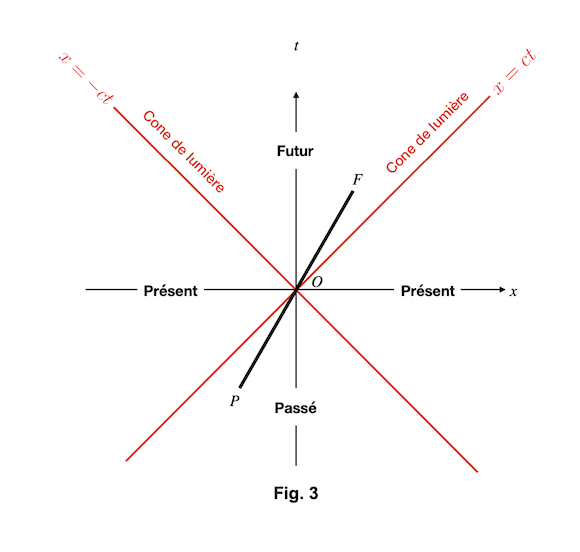
Passé, présent, futur
L'importance de l'équation (9) est qu'elle nous donne une métrique spatio-temporelle (dite la métrique de Minkowski), par laquelle nous pouvons mesurer la séparation entre deux évenements.
Considérons un point O dans l'espace-temps. Les courbes noires en Fig. 3 nous montrent des trajectoires possibles pour des corps matériaux (massifs). Les lignes rouges correspondent aux trajectoires des rayons lumineux. Ensemble, la totalité des lignes rouges forme une surface biconique, qui définit le cône de lumière de l'événement O. Les lignes jaunes correspondent à des trajectoires interdites. Pour les parcourir, il faudrait se déplacer plus vite que la lumière.
Le passé de l'événement O sont tous les événements dont O aurait pu venir à connaissance et qui auraient pu l'influencer. Pour qu'un événement P puisse influencer O, il faut que de la matière ou de la lumière puisse aller de P à O. P doit donc se situer dans le cône de lumière inférieur, qui correspond au passé de O.
Le futur de O sont tous les événements qui pourront être influencés par O. Pour qu'un événement F puisse être influencé par O, il faut que de la matière ou de la lumière puisse aller de O à F. F doit donc se situer dans le cône de lumière supérieur, qui correspond au futur de O.
Le présent de O sont tous les événements qui n'appartiennent ni à son passé ni à son futur, c'est-à-dire tout ce qui est en dehors son cône de lumière.
L'équation (9) montre que la "distance" spatio-temporelle 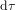 entre O et n'importe quel point sur la surface du cône de lumière est nulle. Avec la définition de distance (c'est-à-dire avec la métrique) en équation (9), la distances entre O et les points A et B en Fig. 3 sont nulles. Cela est logique. Les chemins AO et OB correpondent aux trajectoires d'un rayon de lumière. Pour la lumière, le temps ne passe pas. Donc, pour elle, ces chemins prennent un temps
entre O et n'importe quel point sur la surface du cône de lumière est nulle. Avec la définition de distance (c'est-à-dire avec la métrique) en équation (9), la distances entre O et les points A et B en Fig. 3 sont nulles. Cela est logique. Les chemins AO et OB correpondent aux trajectoires d'un rayon de lumière. Pour la lumière, le temps ne passe pas. Donc, pour elle, ces chemins prennent un temps 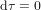 .
.
La distance temporelle, en temps propre, entre P et O ou entre O et F est donnée par 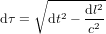 . Le point C appartient au présent de F. La distance temporelle, en temps propre, entre O et C ne correspond à aucun nombre réel parce que, pour les points en dehors du cône de lumière,
. Le point C appartient au présent de F. La distance temporelle, en temps propre, entre O et C ne correspond à aucun nombre réel parce que, pour les points en dehors du cône de lumière, 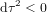 . La distance entre les événements O et C n'est pas temporelle, mais spatiale.
. La distance entre les événements O et C n'est pas temporelle, mais spatiale.
De la même manière que nous avons introduit l'intervalle de temps propre 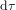 , nous aurions pû introduire la distance propre
, nous aurions pû introduire la distance propre 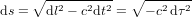 , qui est définie pour tous les événements dans le présent de O, mais devient imaginaire pour les événements passés ou futurs.
, qui est définie pour tous les événements dans le présent de O, mais devient imaginaire pour les événements passés ou futurs.
En conclusion, la métrique relativiste en équation (9) permet de définir une distance en quatre dimensions entre un observateur O et n'importe quel autre événement dans l'espace-temps (un observateur est un événement parce que l'observation est toujours faite à un temps et dans un endroit précis). La distance est temporelle (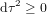 ) pour les événements passés ou futurs. Elle est spatiale (
) pour les événements passés ou futurs. Elle est spatiale (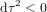 ) pour les événements présents.
) pour les événements présents.
De la relativité restreinte à la relativité générale
La métrique de Minkowski en équation (9) est la métrique de la théorie de la relativité restreinte. Elle prend en compte la relativité de l'espace et du temps, mais elle est restreinte à un univers plat, qui suit la géométrie euclidienne. Elle ne prend pas en compte les effets de la gravité.
Pour prendre en compte la gravité, il faut passer de la théorie de la relativité restreinte à la théorie de la relativité générale, c'est-à-dire à une métrique plus complexe, de la forme :
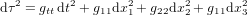 (10),
(10),
où 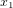 ,
, 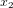 et
et 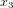 sont les coordonnées spatiales, qui peuvent être les coordonnées cartesiennes orthogonales x, y et z, mais qui pourraient aussi être des coordonnées sphériques, cylindriques, etc.
sont les coordonnées spatiales, qui peuvent être les coordonnées cartesiennes orthogonales x, y et z, mais qui pourraient aussi être des coordonnées sphériques, cylindriques, etc.
On note que, par cohérence dimensionnelle, les coefficients de la métrique ne peuvent pas tous avoir les mêmes unités. Dans la métrique de Minkowski :
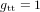 ,
, 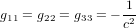 (11)
(11)
Avoir 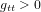 ,
, 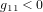 ,
, 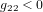 ,
, 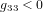 est une propriété générale des métriques dans la théorie de la relativité.
est une propriété générale des métriques dans la théorie de la relativité.
Pour résumer, dans le cas de la théorie de la relativité générale, le mouvement inertiel est le mouvement géodésique. Le chemin géodésique est déterminé par la géométrie et la géométrie est déterminée par la distribution de la matière, qui déforme la structure de l’espace-temps. Une pomme qui chute d’un arbre et la Terre qui tourne autour du Soleil décrivent toutes les deux un chemin géodésique dans leur espace-temps courbe.
Le sommeil agité de la matière
Dans la section précédente, nous avons considéré le mouvement d’une bille sur la surface d’un matelas, sur lequel on a déposé une balle de bowling, qui représente une grande masse, pensée comme statique. Remplaçons maintenant la balle de bowling par un être humain qui s’assoit sur le lit. Les êtres humains ont une différences majeure par rapport aux balles de bowling : ils bougent tout le temps. L’espace-temps est plus similaire à un matelas à ressorts. Quand la matière qui le déforme bouge, il propage des vibrations dans sa géométrie, c’est-à-dire dans les composantes de la métrique 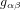 . C'est ça, les ondes gravitationnelles.
. C'est ça, les ondes gravitationnelles.
L’analogie avec les ondes électromagnétiques est évidente. Un courant qui varie avec le temps produit des ondes électromagnétiques - c’est, par ailleurs, comme ça qu’une antenne fonctionne. Une distribution de matière qui varie avec le temps produit des ondes gravitationnelles.
A la vitesse de la lumière
La similarité est aussi présente dans la vitesse de propagation, qui est la vitesse de la lumière dans les deux cas. La raison n’est pas difficile à comprendre si on considère le parcours historique qui a amené d'abord à la théorie de la relativité restreinte, puis à la théorie de la relativité générale. Nous allons résumer ce parcours brièvement.
Un peu d'histoire :
I. - La relativité galiléenne
Au début il y avait la mécanique et la théorie de la gravitation de Newton. En mécanique newtonienne, la vitesse est relative : le voyageur assis est au répos par rapport au wagon, il est un mouvement par rapport à un observateur sur le quai, qui regarde le train partir. Si un corps se déplace à la vitesse  pour un observateur O, il se déplacera à la vitesse :
pour un observateur O, il se déplacera à la vitesse :
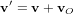
pour un autre observateur O', pour lequel O va à la vitesse 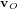 (l'´équation ci-dessus est connue comme la transformation de Galilée). En revanche, l'espace, le temps et l'accélération sont absolus, et la masse est constante. Donc la force
(l'´équation ci-dessus est connue comme la transformation de Galilée). En revanche, l'espace, le temps et l'accélération sont absolus, et la masse est constante. Donc la force 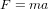 doit être la même dans tous les référentiel inertiels, dans lesquels il n'y a pas de forces apparentes.
doit être la même dans tous les référentiel inertiels, dans lesquels il n'y a pas de forces apparentes.
Cela est bien le cas pour la force gravitationnelle. Dans la théorie de la gravitation de Newton, la force 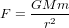 avec laquelle deux corps de masse M et m s'attirent ne dépend que de la distance r entre les deux corps, qui est indépendante du référentiel (le distance entre le passeger et son café est un mètre pour le passager et un mètre pour l'observateur sur le quai). Elle ne dépend pas de leur vitesses.
avec laquelle deux corps de masse M et m s'attirent ne dépend que de la distance r entre les deux corps, qui est indépendante du référentiel (le distance entre le passeger et son café est un mètre pour le passager et un mètre pour l'observateur sur le quai). Elle ne dépend pas de leur vitesses.
II. - Le magnétisme met en crise la relativité galiléenne
La crise de la mécanique classique commence avec la découverte du magnétisme, parce que les forces magnétiques dépendent des vitesses des charges. Une charge au répos ne produit pas de champs magnétique. Donc la présence (ou l'absence) de forces magnétiques devrait dépendre du référentiel, ce qui est incompatible avec la notion que la force est absolue.
Les physiciens de la fin du 19ème siècle se trouvaient donc dans une position très inconfortable. Soit ils abandonnaient les transformations de Galilée, soit ils acceptaient que les lois de l'électromagnétisme n'étaient pas vraies dans tous les référentiels, et alors la question était : quel est le référentiel privilegié, par rapport auquel les vitesses des charges doivent être mesurées ?
III. - Naissance et abandon de l'hypothèse de l'éther
L'hypothèse la plus répandue était celle de l'éther. Les ondes sonores ne voyagent pas dans le vide. Elles ont besoin d'un milieu matériel dans lequel se propager (l'air, l'eau, un mur). La même chose aurait pu valoir – on pensait – pour les ondes électromagnétiques.
Voilà donc l'idée de l'éther, une substance très légère, très fine, qui remplit tout l'espace et qui fournit le milieu dans lequel les ondes électromagnétiques se propagent.
Dans cette vision, l'éther définissait le référentiel privilégié par rapport auquel les vitesses des charges doivent être mesurées pour un calcul correct des forces électromagnétiques.
Einstein refuse la notion de cette substance indétectable. Les équations de l'électromagnétisme prédisent que la lumière doit avoir une vitesse c.
Plutôt que chercher dans quel référentiel cette prédiction est vraie, Einstein suppose que les équations de l'électromagnétisme doivent être vraies pour tous les observateurs inertiels. Donc c est une constante fondamentale de la nature. Si les transformations de Galilée, pour lesquelles toute vitesse dépend du référentiel, sont en conflit avec cette conclusion, c'est eux qu'il faut changer. C'est comme ça que les transformations de Lorentz remplacent les transformations de Galilée.
IV. - Pourquoi une théorie relativiste de la gravitation ?
La théorie de la relativité restreinte remplace les lois de Newton par de nouvelles lois dynamiques invariantes par rapport aux transformations de Lorentz, qui ont donc l’avantage d’être entièrement compatibles avec la théorie électromagnétique. Mais cela laisse ouvert le problème de trouver une nouvelle théorie de la gravitation qui soit invariante par rapport aux transformations de Lorentz (les transformations qui préservent la vitesse de la lumière).
Ce problème est résolu avec la découverte de la théorie de la relativité générale. Les équations d’Einstein, qui donnent 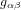 en fonction de la distribution de matière, ont donc été développées exprès de telle manière que la trajectoire d’un photon soit toujours décrite par l'équation :
en fonction de la distribution de matière, ont donc été développées exprès de telle manière que la trajectoire d’un photon soit toujours décrite par l'équation :
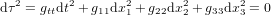 ,
,
qui se reduit à l'équation 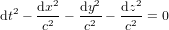 et donc à
et donc à 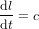 dans le cas sans gravité
dans le cas sans gravité 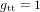 ,
, 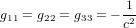 .
.
Constante fondamentales
La théorie de la relativité générale ne contient que deux constantes physiques : la vitesse de la lumière c et la constante de gravitation universelle G. Ensemble avec la constante de Planck h, qui définit l'échelle des phénomènes quantiques, elles constituent les trois constantes de la nature les plus fondamentales.
La constante de gravitation universelle G exprime l’intensité du couplage entre la matière et la géométrie : dans notre comparaison, elle détermine la masse par unité de surface que l’on doit déposer sur un matelas pour obtenir un enfoncement donné. G n’a pourtant aucun effet sur la propagation des ondes gravitationnelles dans le vide, c’est-à-dire, à grande distance des masses qui les ont générées.
La propagation des ondes est un phénomène local
Supposons que des ondes gravitationnelles aient été générées au point A de l’espace. Les ondes se propagent dans le vide du point A au point B, puis du point B au point C.
Pour comprendre la génération des ondes en A et donc la forme des ondes qui arrivent en B, il faut connaître les processus dans la matière qui les ont générées. Mais, supposons connues les caractéristiques des ondes au point B. Le problème de comment les ondes se propagent de B à C n’a rien à faire avec les processus physiques qui engendrèrent cette onde en B. Il n’y a pas d’action à distance. La propagation entre B et C est entièrement déterminée par ce qui se passe entre B et C. Donc, la seule constante physique qui rentre dans cette détermination est la vitesse de la lumière.
Le graviton : une particule à masse nulle
Du point de vue de la physique des particules, le fait que les ondes gravitationnelles se propagent à la vitesse de la lumière est interprété comme une preuve que l’interaction gravitationnelle, aussi bien que l’interaction électromagnétique, se propage par la médiation de particules à masse nulle (respectivement, le graviton et le photon). Les particules de matière intéragissent par l'échange de ces particules médiatrices.
Pour comprendre la raison pour laquelle des particules qui vont à la vitesse de la lumière doivent avoir des masses nulles, considérons une particule de masse au répos 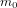 et vitesse
et vitesse 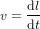 pour laquelle :
pour laquelle :
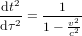 (1)
(1)
et multiplions les termes de cette équation par 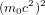 , d'une manière à obtenir :
, d'une manière à obtenir :
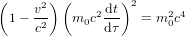 (2).
(2).
Dans cette équation,
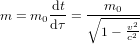 (3)
(3)
est la masse relativiste, qui tend à l'infini pour 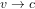 .
.
En utilisant l'équation (3), l'équation (2) peut être réécrite dans la forme :
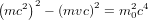 (4),
(4),
qui devient :
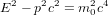 (5),
(5),
si l'on pose :
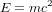
et :
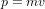
respectivement pour l'énergie et la quantité de mouvement.
Les équations ci-dessus montrent bien que, pour 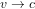 ,
, 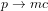 et donc
et donc 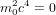 . Une particule qui se déplace a la vitesse de la lumière doit avoir une masse
. Une particule qui se déplace a la vitesse de la lumière doit avoir une masse 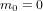 .
.
Les ondes gravitationnelles générées par les mouvements de la matière
Pour mettre en vibration la surface d’un matelas, il faut des corps qui bougent dessus. Plus ils sont lourds et plus rapide est le mouvement, plus fortes seront les oscillations et plus facile sera leur détection. Dans l’Univers, l’exemple le plus extrême de corps massifs qui tournent à grande vitesse l’un autour de l’autre est fourni par les systèmes binaires de trous noirs massifs.
La courbure de l'espace-temps est plus grande quand la matière qui la génère est concentrée dans un petit volume
Une manière intuitive pour comprendre notre intérêt pour les trous noirs consiste à poser sur un matelas un grand livre d’art et une boule en bronze que nous avons choisie pour avoir exactement la même masse que le livre. La masse de la boule est distribuée sur une surface beaucoup plus petite que celle du livre, donc la pression sur les ressorts du matelas est plus forte, raison pour laquelle la boule de bronze s’enfoncera beaucoup plus dans le matelas que le livre d’art.
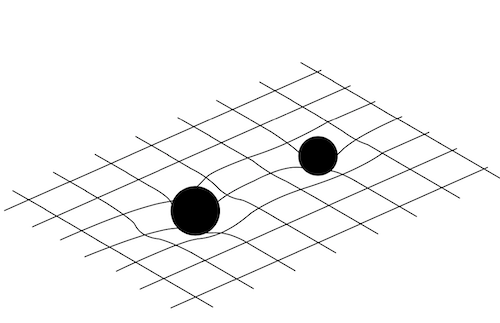
Courbure de l’espace-temps en présence de deux trois noirs. La déformation n’est pas statique parce que les trous noirs tournent autour de leur centre de masse commun . Donc elle se propage comme une vibration dans le tissu de l’espace-temps.
Les trous noirs plient l'espace-temps comme rien d'autre
Les trous noirs sont les corps les plus denses (ceux qui ont la plus grande masse par unité de volume). Donc, ils sont les plus aptes à courber l’espace-temps autour d’eux. La figure montre la courbure de l’espace-temps en présence de deux trous noirs. La déformation n’est pas statique parce que les trous noirs tournent autour de leur centre de masse commun. Donc elle se propage comme une vibration dans le tissu de l’espace-temps.
Le Soleil et la Terre : vitesse de rotation et temps orbital
Pour comprendre les systèmes binaires de trous noirs d’une manière plus quantitative, commençons par le cas, qui nous est beaucoup plus familier, du système Soleil-Terre (Fig. 1).
La vitesse à laquelle la Terre tourne autour du Soleil est déterminée par l’équilibre entre la force gravitationnelle 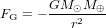 , qui pousse la Terre vers le Soleil, et la force centrifuge
, qui pousse la Terre vers le Soleil, et la force centrifuge 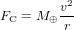 , qui pousse la Terre à s’en éloigner. Ici, G est la constante de gravitation universelle,
, qui pousse la Terre à s’en éloigner. Ici, G est la constante de gravitation universelle, 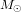 est la masse du Soleil,
est la masse du Soleil, 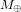 est la masse de la Terre, r est la distance entre la Terre et le Soleil, et v est la vitesse avec laquelle la Terre tourne autour du Soleil. La condition
est la masse de la Terre, r est la distance entre la Terre et le Soleil, et v est la vitesse avec laquelle la Terre tourne autour du Soleil. La condition 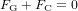 (si la Terre est sur une orbite circulaire, elle ne doit ni s’approcher du Soleil, ni s’en éloigner), donne :
(si la Terre est sur une orbite circulaire, elle ne doit ni s’approcher du Soleil, ni s’en éloigner), donne :
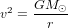 (1).
(1).
Le temps que la Terre prend pour faire un tour complet autour du Soleil (dit aussi la période orbitale) est donc :
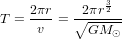 (2).
(2).
L'équation (2) n’exprime rien d’autre que la troisième loi de Kepler : le carré de la période de révolution T est proportionnel au cube du rayon orbital r.
En réalité, la Terre ne tourne pas autour du centre du Soleil, elle tourne autour du centre de masse du Système solaire, mais la masse du Système solaire est tellement dominée par celle du Soleil que l’on peut considérer que les deux sont la même chose.
Cela n’est pas le cas dans un système de deux corps (par exemple, deux trous noirs) de masse comparable. Les calculs sont donc plus compliqués, mais, à la fin, on retrouve l’équation (2) avec, au lieu de 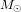 , la masse totale des deux trous corps : une période orbitale courte requiert des corps rapprochés et massifs.
, la masse totale des deux trous corps : une période orbitale courte requiert des corps rapprochés et massifs.
Trous noirs
L’équation (2) montre que des masses élevées et des corps très proches sont la clé pour avoir des oscillations avec une période courte. Le problème est que, normalement, les corps les plus massifs sont aussi les plus grands. Donc, si la masse est grande, il est difficile que r soit petit.
L’intérêt de considérer des trous noirs vient du fait que les trous noirs sont les corps les plus petits qui existent pour une masse donnée.
Pour comprendre pourquoi un trou noir est forcément petit (par rapport à sa masse), il faut revenir à l'équation (1). L'équation (1) nous donne la vitesse de rotation que la
Terre doit avoir pour tourner autour du Soleil sur une orbite circulaire. La vitesse de libération 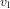 que la Terre devrait avoir pour s'affranchir de l'attraction du Soleil est un peu plus grande, mais pas beaucoup :
que la Terre devrait avoir pour s'affranchir de l'attraction du Soleil est un peu plus grande, mais pas beaucoup :
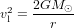 (3).
(3).
Ni  ni
ni 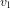 ne dépendent de
ne dépendent de 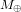 . Ceci est une manifestation du principe d'équivalence.
. Ceci est une manifestation du principe d'équivalence.
L'équation (3) montre que la vitesse de libération 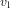 est plus grande quand r est plus petit. Bien entendu, r ne peut jamais être plus petit que la taille de l'objet qui produit l'attraction gravitationnelle. Le rayon
est plus grande quand r est plus petit. Bien entendu, r ne peut jamais être plus petit que la taille de l'objet qui produit l'attraction gravitationnelle. Le rayon
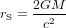 (4)
(4)
auquel 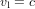 est appelé le rayon de Schwarzschild (c est la vitesse de la lumière). Dans l'équation (4), M est la masse du corps qui génère l'atttraction gravitationnelle. Ce corps n'a pas besoin d'être le Soleil.
est appelé le rayon de Schwarzschild (c est la vitesse de la lumière). Dans l'équation (4), M est la masse du corps qui génère l'atttraction gravitationnelle. Ce corps n'a pas besoin d'être le Soleil.
La masse du Soleil est 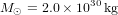 ;
; 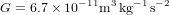 ; donc le rayon du Schwarzschild du Soleil vaut
; donc le rayon du Schwarzschild du Soleil vaut 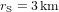 . Le Soleil a un rayon de 700000 km.
S'il était 230000 fois plus petit, tout en gardant la même masse, alors la vitesse de libération du Soleil serait plus grande que la vitesse de la lumière. Donc rien ne pourrait y échapper, même pas sa propre lumière. Si l'on cherche à observer un objet de masse
. Le Soleil a un rayon de 700000 km.
S'il était 230000 fois plus petit, tout en gardant la même masse, alors la vitesse de libération du Soleil serait plus grande que la vitesse de la lumière. Donc rien ne pourrait y échapper, même pas sa propre lumière. Si l'on cherche à observer un objet de masse 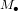 avec une taille :
avec une taille :
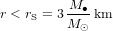 (5),
(5),
tout ce que l'on voit c'est ... un trou noir (Fig. 2), et c'est pour cela que l'on le dénote par le symbole  .
.

Fig. 2
Crédit :
NASA
La Fig. 2 montre la première image d'un trou noir, qui a été rendue publique le 10 avril 2019. Elle a été prise avec le Event Horizon Telescope, qui n'est pas, en réalité, un télescope, mais plutôt un réseau de radiotélescopes à différents endroits sur le globe terrestre. Le trou noir dans l'image se trouve au centre de M87, la galaxie elliptique géante au centre de l'amas de Virgo. Dans la Fig. 2, le trou noir correspond à la région centrale foncée ; la bouée orange est le gaz qui orbite autour du trou noir, avant d'être avalé.
En mai 2022, un deuxième trou noir, celui au centre de notre Galaxie, a été photographié par le même instrument.
La surface sphérique de rayon 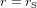 qui enveloppe un trou noir est dite l'horizon des évènements, parce que les évènements à son intérieur sont invisibles. Un trou noir ne peut pas déborder de son horizon ; autrement on verrait sa surface et ce ne serait pas un trou noir. En revanche, il n'y a aucune raison pour que la taille physique d'un trou nour ne puisse pas être plus petite que son horizon. Mais comme cette taille physique est impossible à connaître, c'est toujours le rayon de l'horizon que l'on utilise pour définir la taille d'un trou noir.
qui enveloppe un trou noir est dite l'horizon des évènements, parce que les évènements à son intérieur sont invisibles. Un trou noir ne peut pas déborder de son horizon ; autrement on verrait sa surface et ce ne serait pas un trou noir. En revanche, il n'y a aucune raison pour que la taille physique d'un trou nour ne puisse pas être plus petite que son horizon. Mais comme cette taille physique est impossible à connaître, c'est toujours le rayon de l'horizon que l'on utilise pour définir la taille d'un trou noir.
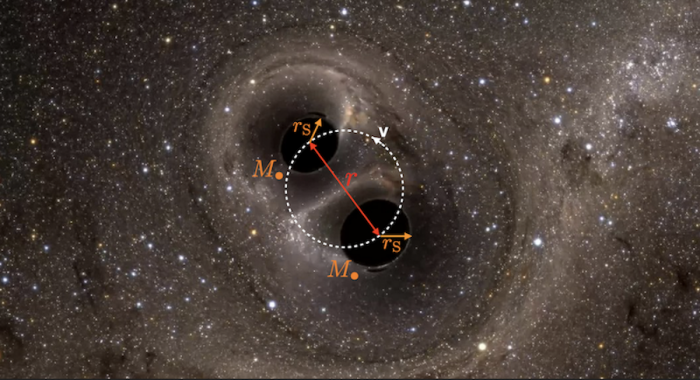
Crédit :
A. Cattaneo from NASA image
Période des ondes gravitationnelles pour un système de deux trous noirs
La distance minimale entre deux trous noirs est 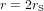 et correspond au cas de deux trous noirs en contact. Issue d'une simulation à l'ordinateur, la Fig. 3 montre deux trous noirs très proches l'un de l'autre, qui orbitent l'un autour de l'autre (le cercle blanc pointillé montre leur orbite autour du centre de masse du système binaire ). Si le deux trous noirs ont la même masse
et correspond au cas de deux trous noirs en contact. Issue d'une simulation à l'ordinateur, la Fig. 3 montre deux trous noirs très proches l'un de l'autre, qui orbitent l'un autour de l'autre (le cercle blanc pointillé montre leur orbite autour du centre de masse du système binaire ). Si le deux trous noirs ont la même masse 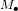 , la masse totale à insérer dans l'équation (2) est
, la masse totale à insérer dans l'équation (2) est 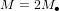 et la période orbitale vaut :
et la période orbitale vaut :
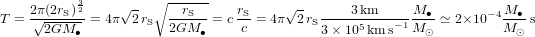 (6).
(6).
Pour un système de deux trous noirs en contact avec une masse identique de 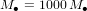 chacun (dans cet exemple, chaque trou noir a une masse égale à mille fois celle du Soleil), l’équation (6) donne
chacun (dans cet exemple, chaque trou noir a une masse égale à mille fois celle du Soleil), l’équation (6) donne 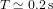 . Un tel système est suffisamment massif et compact pour produire des oscillations significatives dans la géométrie de l’espace-temps et il est capable de produire un signal avec une fréquence que l’on pourrait, à priori, mesurer avec des instruments de laboratoire.
. Un tel système est suffisamment massif et compact pour produire des oscillations significatives dans la géométrie de l’espace-temps et il est capable de produire un signal avec une fréquence que l’on pourrait, à priori, mesurer avec des instruments de laboratoire.
En réalité, le système binaire que nous avons décrit ne peut pas exister comme système stable dans la mécanique relativiste, parce que, à la différence du cas newtonien, dans lequel l’énergie est conservée, il perd de l’énergie par émission d’ondes gravitationnelles.
L’énergie que les trous noirs utilisent pour mettre en vibration l’espace-temps doit venir de quelque part. Elle vient de l'énergie cinétique de rotation des trous noirs eux-mêmes. Comme pour la révolution terrestre, les trous noirs sont maintenus sur un orbite circulaire l'un autour de l'autre par l'équilbre entre la force gravitationnelle et la force centrifuge. Si la force centrifuge diminue, parce que les trous noirs sont freinés par l'émission d'ondes gravitationnelles, alors la gravité va prévaloir, et les trous noirs se rapprochent jusqu’à tomber l’un sur l’autre.
Le processus accélère quand la distance entre les trous noirs diminue et l’émission d’ondes gravitationnelles devient plus importante. Une fois que la distance entre les trous noirs est comparable à la taille des trous noirs eux-mêmes, la coalescence se passe dans une fraction de seconde. Il s'ensuit que les ondes gravitationnelles générées par un système binaire de trous noirs ne sont détectables que pour un temps très court. Avant, le signal est trop faible. Après, il n’y a plus de signal parce qu’il n’y a qu’un seul trou noir.
Effet sur la matière
Pour comprendre comment l’on peut détecter une onde gravitationnelle, il faut se demander qu’est-ce qui se passe pour la matière quand l’amplitude caractéristique h des termes non nuls de la matrice 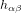 oscille autour de sa valeur normale,
oscille autour de sa valeur normale, 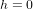 .
.
Considérons donc le cadran d’une montre imaginaire et huit particules disposées à 1h30, 3h, 4h30, 6h, 7h30, 9h, 10h30 et 12h (Figure ci-dessous). Soit r le rayon du cercle qui passe par les huit particules. Les positions des huit particules sont perturbées par le passage d’une onde gravitationnelle sinusoïdale avec une période T. Nous choisissons le temps 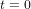 de telle manière que
de telle manière que 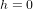 pour
pour 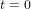 . A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.
. A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.
A 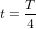 , h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :
, h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :
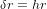 (1).
(1).
A 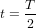 ,
, 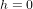 . Donc, les particules sont revenues à la position initiale. A
. Donc, les particules sont revenues à la position initiale. A 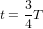 ,
, 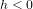 , donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à
, donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à 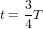 a la même forme que l’ellipse à
a la même forme que l’ellipse à 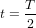 tournée de 90˚. A
tournée de 90˚. A 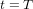 , les particules reviennent pour la deuxième fois à la position initiale.
, les particules reviennent pour la deuxième fois à la position initiale.
L’effet du passage de l’onde gravitationnelle est donc celui de générer une vibration de la structure de l’espace-temps qui met en oscillation toutes les longueurs.
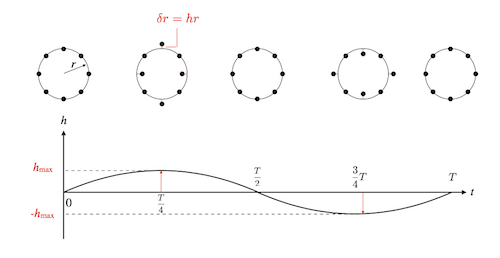
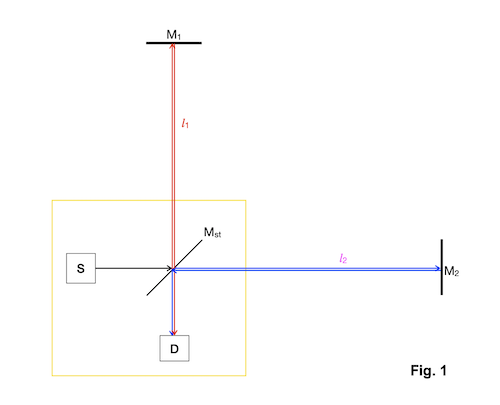
L'interférométrie
L’instrument que l’on utilise pour mesurer des variations de distance très très petites est un interféromètre. La raison de ce nom nous sera claire bientôt. Le principe de fonctionnement d’un interféromètre consiste à utiliser un système de miroirs pour faire arriver un faisceau laser d’une source à un détecteur en lui faisant emprunter deux chemins différents, 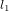 et
et 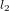 (Fig. 1).
(Fig. 1).
Un faisceau laser sort de la source S, située dans le bâtiment principal, dont les murs sont marqués en jaune. Le faisceau laser rencontre le miroir semi-transparent (la plaque séparatrice de verre semi-argentée) 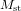 . Une partie de la lumière est réfléchie et redirigée vers le miroir
. Une partie de la lumière est réfléchie et redirigée vers le miroir 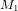 . Une autre partie continue son chemin en ligne droite vers le miroir
. Une autre partie continue son chemin en ligne droite vers le miroir 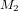 . La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers
. La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers 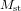 . Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers
. Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers  . Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.
. Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.
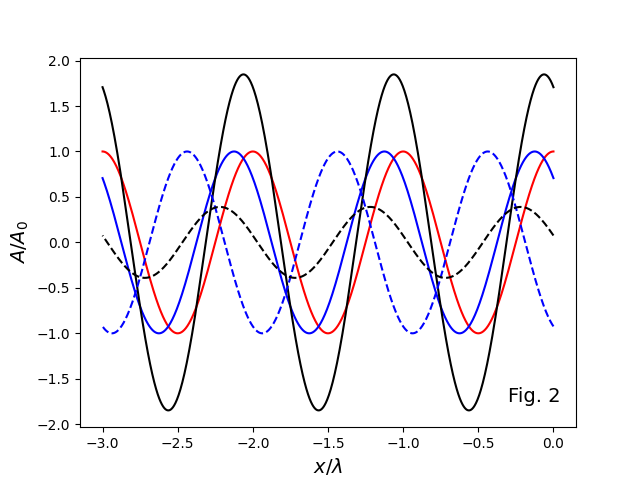
Les ondes monochromatiques qui arrivent au détecteur par les deux chemins ont été émises avec la même phase, s’agissant du même faisceau laser qui a été séparé en deux, mais elles y arriveront avec des phases différentes si les longueurs 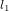 et
et 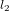 des deux chemins après leur séparation sont
des deux chemins après leur séparation sont 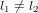 . Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins
. Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins 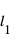 et
et 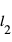 est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (
est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (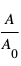 est le rapport entre l’amplitude
est le rapport entre l’amplitude 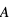 mesurée par le détecteur et l’amplitude
mesurée par le détecteur et l’amplitude 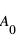 émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin
émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin 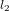 (5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
(5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
En général, 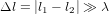 , où
, où  est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si
est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si 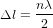 et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si
et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si 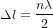 et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.
et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.
Interféromètres

Interféromètres LIGO (Hanford à gauche et Livingston au centre) et VIRGO (à droite)
Crédit :
MIT-CNRS
Les principaux interféromètres pour la détection d’ondes gravitationnelles sont construits à Hanford (Washington) et Livingstone (Louisiane) par la collaboration américaine LIGO, et à proximité de Pise par la collaboration franco-italienne VIRGO. Un quatrième interféromètre, beaucoup plus petit, a aussi été construit à Hanover par la collaboration anglo-allemande GEO600. D’autres interféromètres seront bientôt opérationnels.
Dans les trois cas, l’interféromètre est constitué d’une unité centrale et de deux bras, qui font 4 km de long dans le cas de LIGO, 3 km de long dans le cas de VIRGO et 600 m de long dans le cas de GEO600. L’unité centrale contient la source laser, le détecteur et la lame séparatrice, un miroir semi-transparent qui sépare la lumière en un faisceau réfléchi et un faisceau transmis. Les deux faisceaux sont envoyés dans les deux bras de l’interféromètre, des tubes sous vide qui se terminent avec des miroirs qui réfléchissent les deux faisceaux vers l’unité centrale. Des systèmes de miroirs sont utilisés afin que la lumière fasse plusieurs aller-retours dans chaque bras avant d’être envoyée au détecteur, de telle manière que tout se passe comme si les bras étaient des centaines de fois plus longs (la vitesse de la lumière est tellement élevée que la lumière peut faire des centaines d’aller-retours dans un temps court par rapport à la période des ondes gravitationnelles, déterminée par la période orbitale des systèmes binaires qui les produisent).
La difficulté la plus grande est due à la présence de nombreuses sources de bruit qui pourraient mettre en vibration les miroirs d’un interféromètre simulant les effet d’une onde gravitationnelle (activité sismique, vent, circulation routière, bruit thermique). La détection d’une onde gravitationnelle avec au moins deux interféromètres à deux endroits différents de la planète est nécessaire pour exclure ces formes de bruits, qui ne peuvent pas générer la même forme d’onde simultanément à plusieurs milliers de kilomètres de distance.
Détection des ondes gravitationnelles
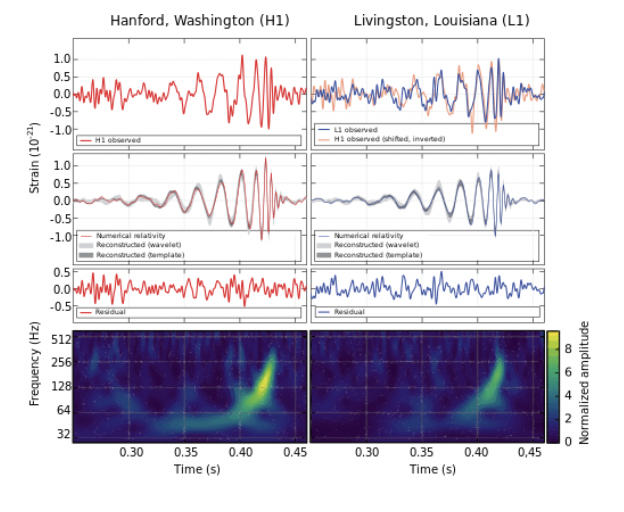
Détection par la collaboration LIGO des ondes gravitationnelles le 14 septembre 2015
Crédit :
LIGO
La première détection d’ondes gravitationnelles a été réalisée aux Etats Unis, par la collaboration LIGO, le 14 septembre 2015, même si la découverte n’a été annoncée que le 11 février 2016, après de nombreuses vérifications. Les miroirs de l'interféromètre de Livingston sont entrés en vibration, puis, 7 millisecondes plus tard, le même phénomène s’est produit dans les miroirs de l’interféromètre de Hanford. La fréquence des oscillations a augmenté et leur amplitude a cru pendant 0,2 seconde, puis elles se sont amorties. Les figures ci-dessus montrent la fréquence du signal mesurée à Livingston et Hanford en fonction du temps.
Ce signal a été appelé GW150914. GW est un acronyme pour Gravitational Waves. Les chiffres qui suivent donnent l’année, le mois et le jour de l’événement. L’amplitude de la perturbation était trop faible pour qu’un être humain puisse s’apercevoir de quoi que ce soit, mais on a remarqué que la fréquence du signal correspondait à des longueurs d’onde audibles. En l’amplifiant énormément, on entend ce qui pourrait ressembler au pépiement d’un oiseau.
Au maximum de l’intensité, la variation de distance entre l’unité centrale et les miroirs au fond des bras a été de un sur 1021 (graphiques sur la première ligne de la figure ci-dessus). La similarité des formes d’onde observées à Livingston et à Hanford (respectivement, la courbe bleue et la courbe rouge dans la figure en haut à droite), ainsi bien que la presque simultanéité des deux détections, cohérente avec une perturbation qui voyage à la vitesse de la lumière (la distance entre Hanford et Livingstone est d’environ 2000 km) supporte fortement l’interprétation que le signal mesuré soit dû au passage d’une onde gravitationnelle. Des ondes sismiques ne pourraient pas se propager à une vitesse supérieure à la vitesse du son dans les roches (de l’ordre de 10 km/s).
Un autre argument qui supporte cette interprétation est la similarité entre la forme d’onde observée et le signal prédit par les simulations numériques des ondes gravitationnelles générées par la coalescence de trous noirs. Les deux graphiques sur la deuxième ligne de la figure ci-dessus comparent ces prédictions (les courbes rouge et bleue dans les graphiques du milieu) à l’évolution de l’amplitude des oscillations, après que celles-ci ont été nettoyées du bruit (les courbes grises au-dessous des courbes rouges et bleues montrent le signal nettoyé). Cette comparaison a non seulement confirmé l’origine gravitationnelle du signal mesuré mais elle a aussi permis de reconstruire certains aspects de l’événement astrophysique qui l’a produit.
Les ondes gravitationnelles viendraient d’un système binaire de trous noirs de 35 et 30 masses solaires. Leur émission correspond aux dernières orbites des deux trous noirs et à leur coalescence finale, qui aboutit à la formation d’un seul trou noir de 62 masses solaires, la masse-énergie des 3 masses solaires manquantes ayant été convertie en ondes gravitationnelles. La puissance émise durant les dernières 20 millisecondes de la coalescence aurait été de 3 x 1056 erg/s, soit 50 fois la puissance lumineuse totale de toutes les étoiles dans l’Univers visible.
Le signal provenait de la direction de la constellation du Sagittaire. A partir de l’amplitude du signal (ou bien de la faiblesse du signal, pour phénomène d'une telle puissance), on a estimé que l’événement s’est passé à une distance de 440 mégaparsecs, donc bien au-delà de l’Univers local. Les ondes gravitationnelles que nous avons détectées le 14 septembre 2015 ont donc voyagé dans l’espace pendant 1,4 milliards d’années avant de nous parvenir.
Cette détection d'ondes gravitationnelles ouvre de nouvelles fenêtres sur l’Univers. Les premiers éléments enthousiasmants sont la détection expérimentale d’un phénomène physique prédit mais non observé, et qu'il s'agit d'une nouvelle confirmation de la théorie de la relativité d’Einstein. L’intérêt des détections suivantes (GW151226, GW170104) et des prochaines porteront plus sur les connaissances astrophysiques qu’elles apportent sur les propriétés des trous noirs et la fréquence de ce type d’événements. Le télescope restera toujours l’instrument principal de l’astronome, mais la détection d’ondes gravitationnelles aussi bien que celle des neutrinos nous offre la possibilité d’étudier les astres par d’autres manières que l’observation de leur lumière.
Les limites les plus importantes au développement de l’astronomie des ondes gravitationnelles restent la taille maximale des interféromètres que l’on peut construire et les bruits dérivant de nombreux phénomènes qui se passent sur notre planète. La prochaine étape sera donc le développement d’un interféromètre dans l’espace. L’Agence Spatiale Européenne a déjà un projet dans ce sens. Il s’agit de LISA (Laser Interferometer Space Antenna). Dans LISA, l’unité centrale et les miroirs au fond des bras seront remplacés par trois astronefs séparées par des distances de millions de kilomètres. La mission LISA devrait devenir opérationnelle après 2030. Une étude préliminaire des bruits auxquels on peut s’attendre dans les mesures avec LISA vient d’être plubiée en 2017.





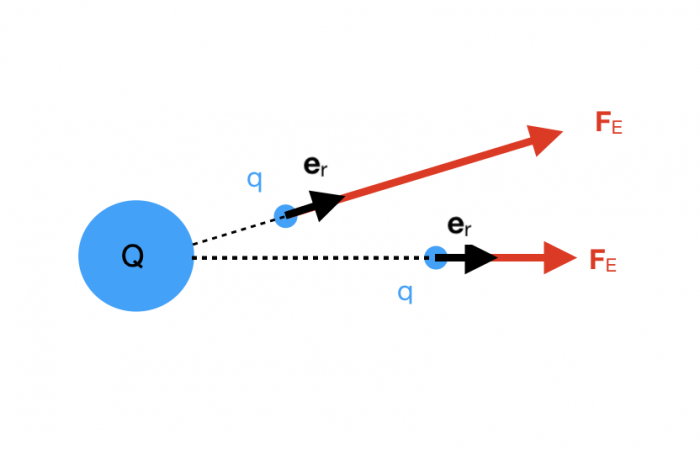
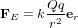 , où r est la distance qui sépare les charges,
, où r est la distance qui sépare les charges, 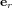 est un vecteur de longueur unitaire dirigé de Q vers q et
est un vecteur de longueur unitaire dirigé de Q vers q et 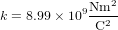 est la constante de Coulomb (en unités du Système International, où le newton est l'unité de force, le mètre est l'unité de longeur et le coulombs est l'unité pour la quantité de charge).
est la constante de Coulomb (en unités du Système International, où le newton est l'unité de force, le mètre est l'unité de longeur et le coulombs est l'unité pour la quantité de charge). 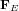 est positive (répulsive) si les deux charges ont le même signe et négative (attractive) si elles ont des signes opposés.
est positive (répulsive) si les deux charges ont le même signe et négative (attractive) si elles ont des signes opposés.
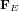 que la charge Q exerce sur la charge q pour différentes positions de cette dernière. La force est plus intense quand la distance r entre q et Q est plus petite. Le module du vecteur
que la charge Q exerce sur la charge q pour différentes positions de cette dernière. La force est plus intense quand la distance r entre q et Q est plus petite. Le module du vecteur 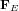 est quatre fois plus grand quand la distance entre q et Q est deux fois plus petite.
est quatre fois plus grand quand la distance entre q et Q est deux fois plus petite.
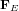 peut être réécrite comme
peut être réécrite comme 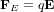 , où
, où 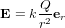 est le champ électrique.
est le champ électrique.
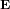 ne dépend que de la charge Q qui génère le champ et de la position par rapport à elle. Différemment de la force électrique
ne dépend que de la charge Q qui génère le champ et de la position par rapport à elle. Différemment de la force électrique 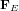 , le champ électrique
, le champ électrique 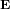 ne dépend pas de la charge d’essai q qui en subit les effets.
ne dépend pas de la charge d’essai q qui en subit les effets.
 ) définie en chaque point de l’espace.
) définie en chaque point de l’espace.
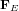 pour différentes positions de la charge q, nous pouvons tracer les lignes de force pour le champ électrique
pour différentes positions de la charge q, nous pouvons tracer les lignes de force pour le champ électrique 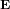 , qui donnent sa direction en chaque point de l’espace.
, qui donnent sa direction en chaque point de l’espace.
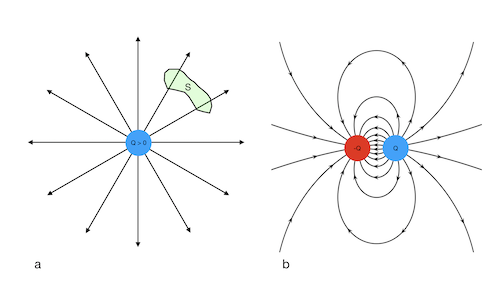


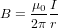 (loi de Biot-Savart), où I est l'intensité du courant dans le fil et
(loi de Biot-Savart), où I est l'intensité du courant dans le fil et 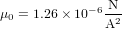 est une constante fondamentale, appelée perméabilité magnétique du vide. Son rôle dans le magnétisme équivaut à celui de la constante de Coulomb dans l'électricité. Les charges sont les sources du champ électrique. Les courants sont les sources du champs magnétique. La constante de Coulomb donne l'intensité du champ électrique par unité de quantité de charge. La perméabilité magnétique du vide donne l'intensité du champ magnétique par unité d'intensité de courant (newton [N] et ampère [A] sont les unités, respectivement, de force et de courant dans le Système International).
est une constante fondamentale, appelée perméabilité magnétique du vide. Son rôle dans le magnétisme équivaut à celui de la constante de Coulomb dans l'électricité. Les charges sont les sources du champ électrique. Les courants sont les sources du champs magnétique. La constante de Coulomb donne l'intensité du champ électrique par unité de quantité de charge. La perméabilité magnétique du vide donne l'intensité du champ magnétique par unité d'intensité de courant (newton [N] et ampère [A] sont les unités, respectivement, de force et de courant dans le Système International).
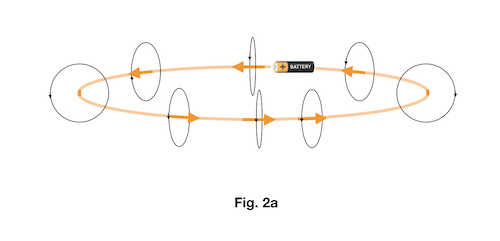
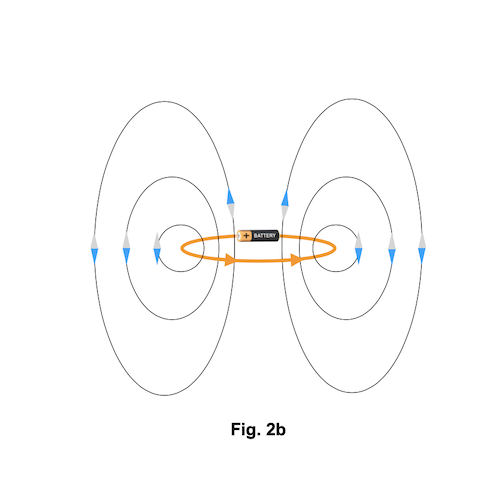
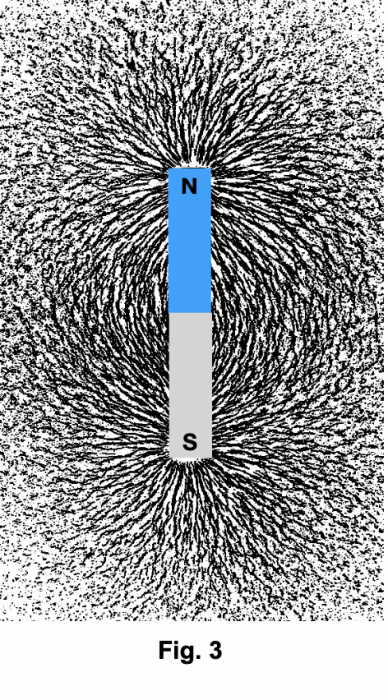
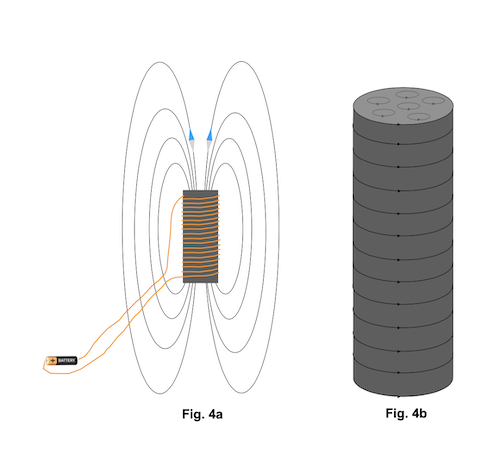


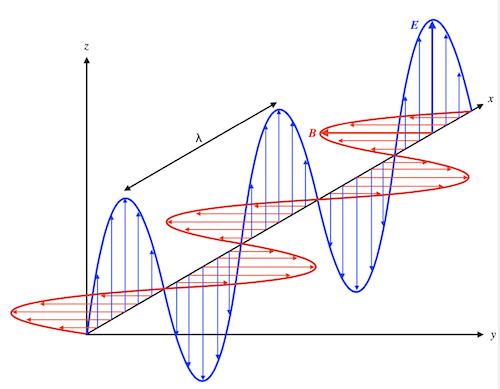
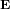 et le champ magnétique
et le champ magnétique 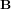 dans une onde électromagnétique qui se propage dans la direction de l'axe x. Le champ électrique (en bleu) vibre dans le plan xy. Le champ magnétique (en rouge) vibre dans le plan xz.
dans une onde électromagnétique qui se propage dans la direction de l'axe x. Le champ électrique (en bleu) vibre dans le plan xy. Le champ magnétique (en rouge) vibre dans le plan xz.  est la longueur d'onde.
est la longueur d'onde.
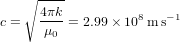 .
.
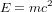 . Les particules qui composent le champ électromagnétique – les photons – n’ont pas de masse, alors que les protons, les neutrons et les électrons en ont une, mais cela ne rend pas la lumière moins physiquement réelle qu’une pomme.
. Les particules qui composent le champ électromagnétique – les photons – n’ont pas de masse, alors que les protons, les neutrons et les électrons en ont une, mais cela ne rend pas la lumière moins physiquement réelle qu’une pomme.
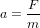 . Dans le cas de l'électricité, la force F avec laquelle deux charges s'attirent ne dépend de leurs masses (les masses apparaissent nulle part dans la loi de Coulomb). Donc, l’accélération a sera plus grande pour un corps moins massif et plus petite pour un corps plus massif.
. Dans le cas de l'électricité, la force F avec laquelle deux charges s'attirent ne dépend de leurs masses (les masses apparaissent nulle part dans la loi de Coulomb). Donc, l’accélération a sera plus grande pour un corps moins massif et plus petite pour un corps plus massif.
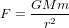 , où r est la distance entre les deux masses et G est la constante de gravitation universelle. Donc, l'accélération de la masse m due à l'attraction gravitationnelle de la masse M,
, où r est la distance entre les deux masses et G est la constante de gravitation universelle. Donc, l'accélération de la masse m due à l'attraction gravitationnelle de la masse M, 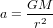 , ne dépend pas de m. L'accélération gravitationnelle est la même pour un pomme de 200 g et une balle de canon de 5 kg. Si on laisse chuter un pomme de 200 g et une balle de canon de 5 kg de la même hauteur, elles arriveront au sol en même temps, si on néglige la résistance de l'air.
, ne dépend pas de m. L'accélération gravitationnelle est la même pour un pomme de 200 g et une balle de canon de 5 kg. Si on laisse chuter un pomme de 200 g et une balle de canon de 5 kg de la même hauteur, elles arriveront au sol en même temps, si on néglige la résistance de l'air.


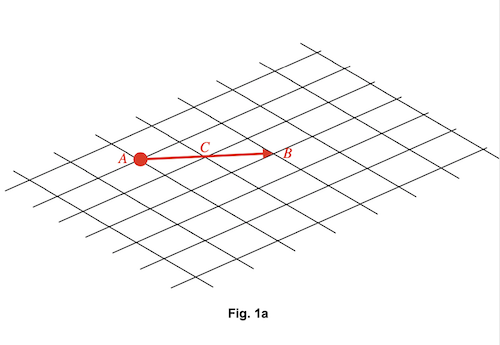
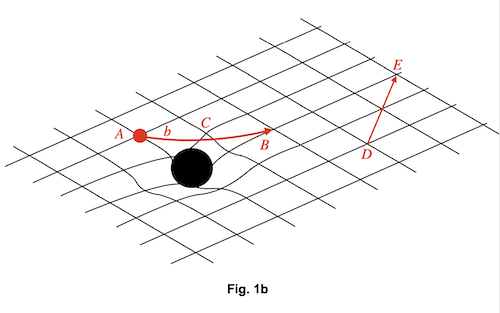


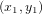 et
et 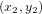 , respectivement sur le plan cartésien (Fig. 1). La distance dl entre les deux points est donnée par le théorème de Pythagore :
, respectivement sur le plan cartésien (Fig. 1). La distance dl entre les deux points est donnée par le théorème de Pythagore :
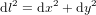 (1),
(1),
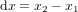 et
et 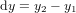 .
.
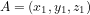 et
et 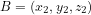 dans l'espace en trois dimensions. En appliquant deux fois le théorème de Pythagore (Fig. 2), nous trouvons :
dans l'espace en trois dimensions. En appliquant deux fois le théorème de Pythagore (Fig. 2), nous trouvons :
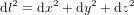 (2).
(2).
 que la droite OA forme avec une droite de référence (en Fig. 1, l'axe x). Dans ce système de coordonnées, la distance
que la droite OA forme avec une droite de référence (en Fig. 1, l'axe x). Dans ce système de coordonnées, la distance 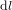 entre les points
entre les points 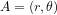 et
et 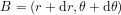 est déterminée par l'équation :
est déterminée par l'équation :
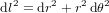 (3),
(3),
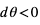 ).
).
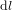 entre deux points*. Un changement de métrique est – nous le verrons bientôt – quelque chose de plus profond.
entre deux points*. Un changement de métrique est – nous le verrons bientôt – quelque chose de plus profond.
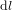 est correct dans la limite que
est correct dans la limite que 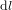 est infinitésimale. Autrement, on ne peut pas traiter l'arc de cercle de longueur
est infinitésimale. Autrement, on ne peut pas traiter l'arc de cercle de longueur 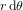 comme un segment et l'on ne peut pas supposer qu'il soit perpendiculaire au segment de longueur
comme un segment et l'on ne peut pas supposer qu'il soit perpendiculaire au segment de longueur 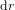 .
.
 et la longitude
et la longitude 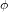 , étant donné que la distance r du centre de la Terre est la même pour tous les points. A
, étant donné que la distance r du centre de la Terre est la même pour tous les points. A 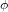 , constante, une variation infinitésimale
, constante, une variation infinitésimale 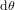 de la latitude correspond à un déplacement de
de la latitude correspond à un déplacement de 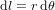 , si les angles sont exprimés en radians. A
, si les angles sont exprimés en radians. A  constante, une variation infinitésimale
constante, une variation infinitésimale 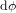 de la longitude correspond à un déplacement de
de la longitude correspond à un déplacement de 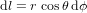 . Dans la limite où des arcs infinitésimaux peuvent être considérés comme rectilignes, le théorème de Pythagore donne :
. Dans la limite où des arcs infinitésimaux peuvent être considérés comme rectilignes, le théorème de Pythagore donne :
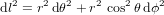 (4).
(4).
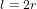 . La métrique (4) correspond au deuxième cas,
. La métrique (4) correspond au deuxième cas, 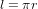 . La métrique (4) est non-euclidienne parce qu'elle mesure les distances sur une surface courbe.
. La métrique (4) est non-euclidienne parce qu'elle mesure les distances sur une surface courbe.
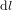 entre le point de coordonnées
entre le point de coordonnées 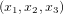 et le point de coordonnées
et le point de coordonnées 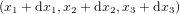 est donnée par la formule :
est donnée par la formule :
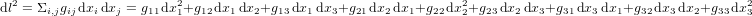 (5).
(5).
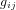 dans l'équation (5) définit la métrique. Dans un système de coordonnées cartesiennes orthogonales,
dans l'équation (5) définit la métrique. Dans un système de coordonnées cartesiennes orthogonales, 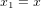 ,
, 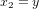 et
et 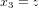 . Dans ce système de coordonnées, la métrique euclidienne prend la forme très simple
. Dans ce système de coordonnées, la métrique euclidienne prend la forme très simple 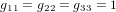 et
et 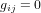 pour
pour 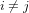 .
.
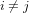 disparaissent localement. On peut démontrer que cette propriété se déduit de la symétrie de la métrique, c'est-à-dire du fait que la distance entre A et B doit être égale à la distance entre B et A. Pour cette raison, nous ne considérerons que des métriques de la forme (dite diagonale) :
disparaissent localement. On peut démontrer que cette propriété se déduit de la symétrie de la métrique, c'est-à-dire du fait que la distance entre A et B doit être égale à la distance entre B et A. Pour cette raison, nous ne considérerons que des métriques de la forme (dite diagonale) :
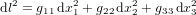 (6).
(6).
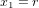 ,
, 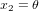 et
et 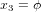 . Nous laissons au lecteur l'exercice de calculer les valeurs des coefficients
. Nous laissons au lecteur l'exercice de calculer les valeurs des coefficients 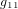 ,
, 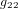 ,
, 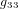 pour la métrique euclidienne dans un tel système de coordonnées.
pour la métrique euclidienne dans un tel système de coordonnées.
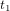 ,
, 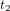 ,
, 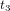 , etc. Imaginez maintenant d’empiler toutes ces photographies instantanées et de tracer une courbe qui connecte les positions du corps dans toutes les photographies instantanées empilées (Fig 1b, courbe bleue continue). Voici la trajectoire du corps dans l’espace-temps. En relativité, on appelle cette trajectoire une ligne d'univers.
, etc. Imaginez maintenant d’empiler toutes ces photographies instantanées et de tracer une courbe qui connecte les positions du corps dans toutes les photographies instantanées empilées (Fig 1b, courbe bleue continue). Voici la trajectoire du corps dans l’espace-temps. En relativité, on appelle cette trajectoire une ligne d'univers.

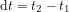 , que nous considérons comme un intervalle de temps infinitésimal, et soient dx, dy, dz les variations entre
, que nous considérons comme un intervalle de temps infinitésimal, et soient dx, dy, dz les variations entre 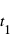 et
et 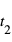 des coordonnées spatiales du corps représenté par le cercle bleu en Fig. 1.
des coordonnées spatiales du corps représenté par le cercle bleu en Fig. 1.
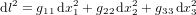 , qui se réduit à
, qui se réduit à 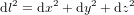 pour la métrique euclidienne en coordonnées cartésiennes. En Fig. 1, les cercles verts montrent la position initiale du corps ; d
pour la métrique euclidienne en coordonnées cartésiennes. En Fig. 1, les cercles verts montrent la position initiale du corps ; d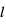 est le déplacement par rapport à la position initiale.
est le déplacement par rapport à la position initiale.
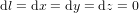 . Pour ce corps, le seul changement est le temps
. Pour ce corps, le seul changement est le temps 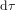 qui s'écoule entre les évènements* A et B. Ce temps-ci est appelé temps propre, parce que c’est le temps dans le référentiel du corps (le référentiel dans lequel le corps est au repos). Le temps propre est indiqué avec la lettre grecque
qui s'écoule entre les évènements* A et B. Ce temps-ci est appelé temps propre, parce que c’est le temps dans le référentiel du corps (le référentiel dans lequel le corps est au repos). Le temps propre est indiqué avec la lettre grecque  pour le distinguer du temps t dans le référentiel de l'observateur . La théorie de la relativité s'appelle comme ça parce que le temps n'est pas absolu. Son écoulement dépend de l'observateur qui le mesure.
pour le distinguer du temps t dans le référentiel de l'observateur . La théorie de la relativité s'appelle comme ça parce que le temps n'est pas absolu. Son écoulement dépend de l'observateur qui le mesure.
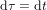 par définition, mais comment mettre en relation le temps propre
par définition, mais comment mettre en relation le temps propre  mesuré par un astronaute qui voyage dans un vaisseau spatial avec le temps t mésuré par un observateur externe, pour lequel l'astronaute se déplace à grande vitesse ? Les transformations de Lorentz répondent à cette question.
mesuré par un astronaute qui voyage dans un vaisseau spatial avec le temps t mésuré par un observateur externe, pour lequel l'astronaute se déplace à grande vitesse ? Les transformations de Lorentz répondent à cette question.

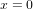 . L'astronaute qui pilote l'astronef et la tour de contrôle sur O ont synchronisé leurs montres à l'instant de départ
. L'astronaute qui pilote l'astronef et la tour de contrôle sur O ont synchronisé leurs montres à l'instant de départ 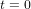 . Pour la tour de contrôle, l'abscisse de l'astronef au temps t est
. Pour la tour de contrôle, l'abscisse de l'astronef au temps t est 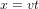 . La ligne droite noire épaisse en Fig. 2 montre la relation entre x et t pour l'astronef dans le référentiel de la tour de contrôle.
. La ligne droite noire épaisse en Fig. 2 montre la relation entre x et t pour l'astronef dans le référentiel de la tour de contrôle.
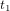 dans son référentiel, la tour de contrôle envoie un message radio à l'astronaute. Le message radio se propage à la vitesse de la lumière (les ondes radio sont des ondes électromagnétiques), donc il va plus vite que l'astronef, même s'il part plus tard. Au temps
dans son référentiel, la tour de contrôle envoie un message radio à l'astronaute. Le message radio se propage à la vitesse de la lumière (les ondes radio sont des ondes électromagnétiques), donc il va plus vite que l'astronef, même s'il part plus tard. Au temps 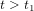 , le message radio a parcouru une distance
, le message radio a parcouru une distance 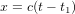 (cette équation correspond à la ligne rouge continue). Quand le message parvient à l'atronaute, l'astronaute répond tout de suite. Les traits rouges montrent la ligne d'univers du message de réponse. La tour de contrôle reçoit la réponse au temps
(cette équation correspond à la ligne rouge continue). Quand le message parvient à l'atronaute, l'astronaute répond tout de suite. Les traits rouges montrent la ligne d'univers du message de réponse. La tour de contrôle reçoit la réponse au temps 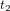 . Nous allons analyser ces événements, d'abord de la perspective de la tour de contrôle, puis de celle de l'astronaute.
. Nous allons analyser ces événements, d'abord de la perspective de la tour de contrôle, puis de celle de l'astronaute.
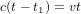 donne
donne 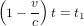 et donc :
et donc :
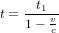 (1).
(1).
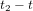 que le message de l'astronaute prend pour parvenir à la tour de contrôle est égal au temps
que le message de l'astronaute prend pour parvenir à la tour de contrôle est égal au temps 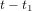 que le message de la tour prend pour parvenir à l'astronaute. La condition
que le message de la tour prend pour parvenir à l'astronaute. La condition 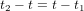 donne :
donne :
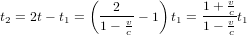 (2).
(2).
 le temps affiché par la montre de l'astronaute quand il reçoit le message de la tour de contrôle. En appliquant le même argument qui amène le personnel de la tour à écrire l'équation (1), l'astronaute conclut que la tour recevra sa réponse au temps :
le temps affiché par la montre de l'astronaute quand il reçoit le message de la tour de contrôle. En appliquant le même argument qui amène le personnel de la tour à écrire l'équation (1), l'astronaute conclut que la tour recevra sa réponse au temps :
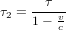 (3)
(3)
 et
et 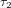 mesurés par l'astronaute et les temps
mesurés par l'astronaute et les temps  et
et 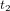 mesurés par la tour. Nous y répondrons en déterminant la valeur du paramètre
mesurés par la tour. Nous y répondrons en déterminant la valeur du paramètre  . Notre calcul se base sur un argument de réciprocité. Si le temps
. Notre calcul se base sur un argument de réciprocité. Si le temps  auquel l'astronaute reçoit le message dans son référentiel est k fois le temps t que la tour a calculé dans son référentiel, alors le temps
auquel l'astronaute reçoit le message dans son référentiel est k fois le temps t que la tour a calculé dans son référentiel, alors le temps 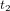 auquel la tour reçoit le message de réponse devra être k fois le temps de réception
auquel la tour reçoit le message de réponse devra être k fois le temps de réception 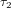 calculé par l'astronaute. Donc :
calculé par l'astronaute. Donc :
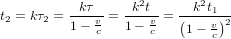 (4),
(4),
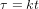 et l'équation (1). Les temps
et l'équation (1). Les temps 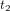 calculés avec l'équation (4) et l'équation (2) doivent être égaux. En posant :
calculés avec l'équation (4) et l'équation (2) doivent être égaux. En posant :
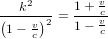 (5)
(5)
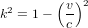 et donc :
et donc :
![\tau^2=\left[1-\left({v\over c}\right)^2\right]t^2](../pages_gravite/equations_gravite-nature/equation96.png) (6).
(6).
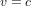 , l'équation (1) donne
, l'équation (1) donne 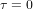 pour n'importe quelle valeur de dt. Pour quelqu'un qui va à la vitesse de la lumière, le temps ne passe pas ! Cela est pourtant impossible pour un corps massif, tel que notre astronef, parce que l'énergie qu'il faudrait pour l'amener à la vitesse de la lumière est infinie. La lumière n'a pas de masse.
pour n'importe quelle valeur de dt. Pour quelqu'un qui va à la vitesse de la lumière, le temps ne passe pas ! Cela est pourtant impossible pour un corps massif, tel que notre astronef, parce que l'énergie qu'il faudrait pour l'amener à la vitesse de la lumière est infinie. La lumière n'a pas de masse.
 et
et  par les temps infinitésimaux
par les temps infinitésimaux 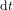 et
et 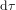 , et réécrire l'équation (6) dans la forme :
, et réécrire l'équation (6) dans la forme :
![{\rm d}\tau^2=\left[1-\left({v\over c}\right)^2\right]{\rm\,d}t^2](../pages_gravite/equations_gravite-nature/equation103.png) (7).
(7).
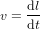 (8).
(8).
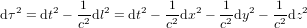 (9),
(9),

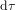 entre O et n'importe quel point sur la surface du cône de lumière est nulle. Avec la définition de distance (c'est-à-dire avec la métrique) en équation (9), la distances entre O et les points A et B en Fig. 3 sont nulles. Cela est logique. Les chemins AO et OB correpondent aux trajectoires d'un rayon de lumière. Pour la lumière, le temps ne passe pas. Donc, pour elle, ces chemins prennent un temps
entre O et n'importe quel point sur la surface du cône de lumière est nulle. Avec la définition de distance (c'est-à-dire avec la métrique) en équation (9), la distances entre O et les points A et B en Fig. 3 sont nulles. Cela est logique. Les chemins AO et OB correpondent aux trajectoires d'un rayon de lumière. Pour la lumière, le temps ne passe pas. Donc, pour elle, ces chemins prennent un temps 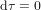 .
.
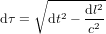 . Le point C appartient au présent de F. La distance temporelle, en temps propre, entre O et C ne correspond à aucun nombre réel parce que, pour les points en dehors du cône de lumière,
. Le point C appartient au présent de F. La distance temporelle, en temps propre, entre O et C ne correspond à aucun nombre réel parce que, pour les points en dehors du cône de lumière, 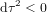 . La distance entre les événements O et C n'est pas temporelle, mais spatiale.
. La distance entre les événements O et C n'est pas temporelle, mais spatiale.
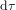 , nous aurions pû introduire la distance propre
, nous aurions pû introduire la distance propre 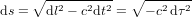 , qui est définie pour tous les événements dans le présent de O, mais devient imaginaire pour les événements passés ou futurs.
, qui est définie pour tous les événements dans le présent de O, mais devient imaginaire pour les événements passés ou futurs.
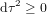 ) pour les événements passés ou futurs. Elle est spatiale (
) pour les événements passés ou futurs. Elle est spatiale (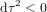 ) pour les événements présents.
) pour les événements présents.
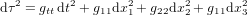 (10),
(10),
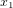 ,
, 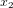 et
et 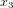 sont les coordonnées spatiales, qui peuvent être les coordonnées cartesiennes orthogonales x, y et z, mais qui pourraient aussi être des coordonnées sphériques, cylindriques, etc.
sont les coordonnées spatiales, qui peuvent être les coordonnées cartesiennes orthogonales x, y et z, mais qui pourraient aussi être des coordonnées sphériques, cylindriques, etc.
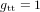 ,
, 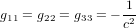 (11)
(11)
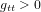 ,
, 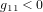 ,
, 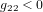 ,
, 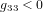 est une propriété générale des métriques dans la théorie de la relativité.
est une propriété générale des métriques dans la théorie de la relativité.
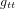 ,
, 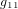 ,
, 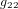 ,
, 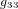 ) et donc la forme du chemin géodésique que les corps vont parcourir sous l'effet de la gravité.
) et donc la forme du chemin géodésique que les corps vont parcourir sous l'effet de la gravité.
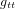 de la métrique est l'équivalent en relativité générale du potentiel gravitationnel en mécanique classique). Notre cours n'a pourtant pas l'objectif de développer des habilités calculatoires. Le but est plutôt de faire comprendre la structure de la théorie de la relativité générale et la conception différente de la gravitation par rapport à la mécanique classique.
de la métrique est l'équivalent en relativité générale du potentiel gravitationnel en mécanique classique). Notre cours n'a pourtant pas l'objectif de développer des habilités calculatoires. Le but est plutôt de faire comprendre la structure de la théorie de la relativité générale et la conception différente de la gravitation par rapport à la mécanique classique.
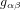 . C'est ça, les ondes gravitationnelles.
. C'est ça, les ondes gravitationnelles.
 pour un observateur O, il se déplacera à la vitesse :
pour un observateur O, il se déplacera à la vitesse :
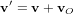
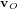 (l'´équation ci-dessus est connue comme la transformation de Galilée). En revanche, l'espace, le temps et l'accélération sont absolus, et la masse est constante. Donc la force
(l'´équation ci-dessus est connue comme la transformation de Galilée). En revanche, l'espace, le temps et l'accélération sont absolus, et la masse est constante. Donc la force 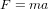 doit être la même dans tous les référentiel inertiels, dans lesquels il n'y a pas de forces apparentes.
doit être la même dans tous les référentiel inertiels, dans lesquels il n'y a pas de forces apparentes.
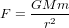 avec laquelle deux corps de masse M et m s'attirent ne dépend que de la distance r entre les deux corps, qui est indépendante du référentiel (le distance entre le passeger et son café est un mètre pour le passager et un mètre pour l'observateur sur le quai). Elle ne dépend pas de leur vitesses.
avec laquelle deux corps de masse M et m s'attirent ne dépend que de la distance r entre les deux corps, qui est indépendante du référentiel (le distance entre le passeger et son café est un mètre pour le passager et un mètre pour l'observateur sur le quai). Elle ne dépend pas de leur vitesses.
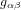 en fonction de la distribution de matière, ont donc été développées exprès de telle manière que la trajectoire d’un photon soit toujours décrite par l'équation :
en fonction de la distribution de matière, ont donc été développées exprès de telle manière que la trajectoire d’un photon soit toujours décrite par l'équation :
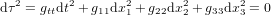 ,
,
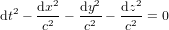 et donc à
et donc à 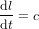 dans le cas sans gravité
dans le cas sans gravité 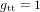 ,
, 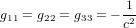 .
.
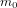 et vitesse
et vitesse 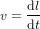 pour laquelle :
pour laquelle :
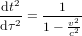 (1)
(1)
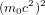 , d'une manière à obtenir :
, d'une manière à obtenir :
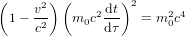 (2).
(2).
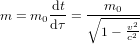 (3)
(3)
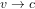 .
.
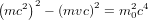 (4),
(4),
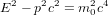 (5),
(5),
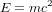
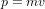
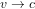 ,
, 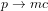 et donc
et donc 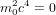 . Une particule qui se déplace a la vitesse de la lumière doit avoir une masse
. Une particule qui se déplace a la vitesse de la lumière doit avoir une masse 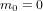 .
.

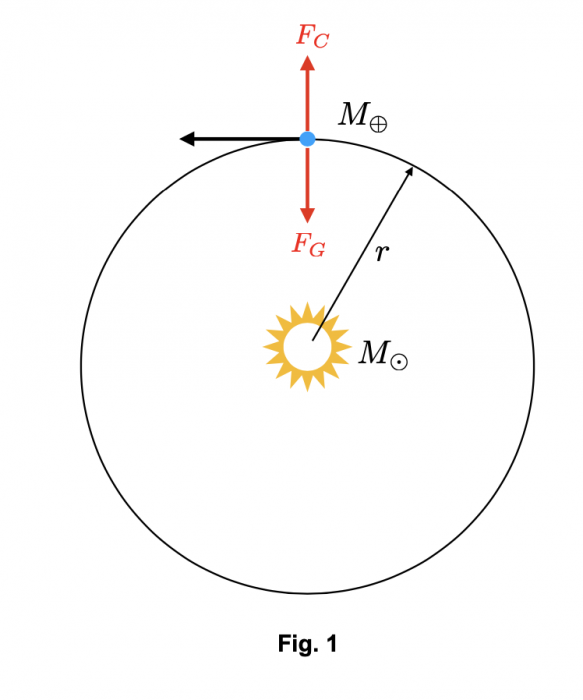
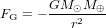 , qui pousse la Terre vers le Soleil, et la force centrifuge
, qui pousse la Terre vers le Soleil, et la force centrifuge 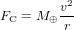 , qui pousse la Terre à s’en éloigner. Ici, G est la constante de gravitation universelle,
, qui pousse la Terre à s’en éloigner. Ici, G est la constante de gravitation universelle, 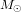 est la masse du Soleil,
est la masse du Soleil, 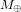 est la masse de la Terre, r est la distance entre la Terre et le Soleil, et v est la vitesse avec laquelle la Terre tourne autour du Soleil. La condition
est la masse de la Terre, r est la distance entre la Terre et le Soleil, et v est la vitesse avec laquelle la Terre tourne autour du Soleil. La condition 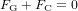 (si la Terre est sur une orbite circulaire, elle ne doit ni s’approcher du Soleil, ni s’en éloigner), donne :
(si la Terre est sur une orbite circulaire, elle ne doit ni s’approcher du Soleil, ni s’en éloigner), donne :
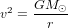 (1).
(1).
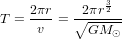 (2).
(2).
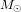 , la masse totale des deux trous corps : une période orbitale courte requiert des corps rapprochés et massifs.
, la masse totale des deux trous corps : une période orbitale courte requiert des corps rapprochés et massifs.
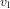 que la Terre devrait avoir pour s'affranchir de l'attraction du Soleil est un peu plus grande, mais pas beaucoup :
que la Terre devrait avoir pour s'affranchir de l'attraction du Soleil est un peu plus grande, mais pas beaucoup :
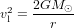 (3).
(3).
 ni
ni 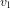 ne dépendent de
ne dépendent de 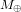 . Ceci est une manifestation du principe d'équivalence.
. Ceci est une manifestation du principe d'équivalence.
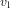 est plus grande quand r est plus petit. Bien entendu, r ne peut jamais être plus petit que la taille de l'objet qui produit l'attraction gravitationnelle. Le rayon
est plus grande quand r est plus petit. Bien entendu, r ne peut jamais être plus petit que la taille de l'objet qui produit l'attraction gravitationnelle. Le rayon
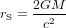 (4)
(4)
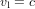 est appelé le rayon de Schwarzschild (c est la vitesse de la lumière). Dans l'équation (4), M est la masse du corps qui génère l'atttraction gravitationnelle. Ce corps n'a pas besoin d'être le Soleil.
est appelé le rayon de Schwarzschild (c est la vitesse de la lumière). Dans l'équation (4), M est la masse du corps qui génère l'atttraction gravitationnelle. Ce corps n'a pas besoin d'être le Soleil.
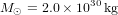 ;
; 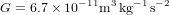 ; donc le rayon du Schwarzschild du Soleil vaut
; donc le rayon du Schwarzschild du Soleil vaut 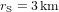 . Le Soleil a un rayon de 700000 km.
S'il était 230000 fois plus petit, tout en gardant la même masse, alors la vitesse de libération du Soleil serait plus grande que la vitesse de la lumière. Donc rien ne pourrait y échapper, même pas sa propre lumière. Si l'on cherche à observer un objet de masse
. Le Soleil a un rayon de 700000 km.
S'il était 230000 fois plus petit, tout en gardant la même masse, alors la vitesse de libération du Soleil serait plus grande que la vitesse de la lumière. Donc rien ne pourrait y échapper, même pas sa propre lumière. Si l'on cherche à observer un objet de masse 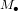 avec une taille :
avec une taille :
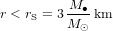 (5),
(5),
 .
.

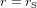 qui enveloppe un trou noir est dite l'horizon des évènements, parce que les évènements à son intérieur sont invisibles. Un trou noir ne peut pas déborder de son horizon ; autrement on verrait sa surface et ce ne serait pas un trou noir. En revanche, il n'y a aucune raison pour que la taille physique d'un trou nour ne puisse pas être plus petite que son horizon. Mais comme cette taille physique est impossible à connaître, c'est toujours le rayon de l'horizon que l'on utilise pour définir la taille d'un trou noir.
qui enveloppe un trou noir est dite l'horizon des évènements, parce que les évènements à son intérieur sont invisibles. Un trou noir ne peut pas déborder de son horizon ; autrement on verrait sa surface et ce ne serait pas un trou noir. En revanche, il n'y a aucune raison pour que la taille physique d'un trou nour ne puisse pas être plus petite que son horizon. Mais comme cette taille physique est impossible à connaître, c'est toujours le rayon de l'horizon que l'on utilise pour définir la taille d'un trou noir.

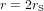 et correspond au cas de deux trous noirs en contact. Issue d'une simulation à l'ordinateur, la Fig. 3 montre deux trous noirs très proches l'un de l'autre, qui orbitent l'un autour de l'autre (le cercle blanc pointillé montre leur orbite autour du centre de masse du système binaire ). Si le deux trous noirs ont la même masse
et correspond au cas de deux trous noirs en contact. Issue d'une simulation à l'ordinateur, la Fig. 3 montre deux trous noirs très proches l'un de l'autre, qui orbitent l'un autour de l'autre (le cercle blanc pointillé montre leur orbite autour du centre de masse du système binaire ). Si le deux trous noirs ont la même masse 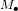 , la masse totale à insérer dans l'équation (2) est
, la masse totale à insérer dans l'équation (2) est 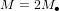 et la période orbitale vaut :
et la période orbitale vaut :
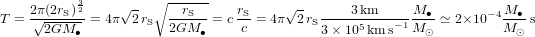 (6).
(6).
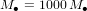 chacun (dans cet exemple, chaque trou noir a une masse égale à mille fois celle du Soleil), l’équation (6) donne
chacun (dans cet exemple, chaque trou noir a une masse égale à mille fois celle du Soleil), l’équation (6) donne 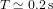 . Un tel système est suffisamment massif et compact pour produire des oscillations significatives dans la géométrie de l’espace-temps et il est capable de produire un signal avec une fréquence que l’on pourrait, à priori, mesurer avec des instruments de laboratoire.
. Un tel système est suffisamment massif et compact pour produire des oscillations significatives dans la géométrie de l’espace-temps et il est capable de produire un signal avec une fréquence que l’on pourrait, à priori, mesurer avec des instruments de laboratoire.
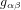 qui définissent la métrique.
qui définissent la métrique.
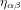 , pour laquelle
, pour laquelle 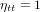 ,
, 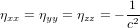 et
et 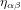 quand
quand 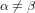 . La personne qui a failli recevoir un pot de fleurs sur la tête ne partagera bien sûr pas cet avis, mais c’est la raison pour laquelle l’amplitude des ondes gravitationnelles est donnée par la matrice :
. La personne qui a failli recevoir un pot de fleurs sur la tête ne partagera bien sûr pas cet avis, mais c’est la raison pour laquelle l’amplitude des ondes gravitationnelles est donnée par la matrice :
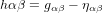 (1),
(1),
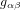 et la métrique de Minkowski
et la métrique de Minkowski 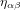 .
.
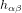 correspond donc à une perturbation de la métrique.
correspond donc à une perturbation de la métrique.
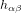 oscille autour de sa valeur normale,
oscille autour de sa valeur normale, 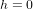 .
.
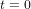 de telle manière que
de telle manière que 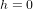 pour
pour 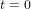 . A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.
. A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.
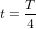 , h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :
, h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :
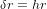 (1).
(1).
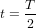 ,
, 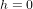 . Donc, les particules sont revenues à la position initiale. A
. Donc, les particules sont revenues à la position initiale. A 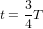 ,
, 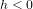 , donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à
, donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à 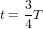 a la même forme que l’ellipse à
a la même forme que l’ellipse à 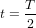 tournée de 90˚. A
tournée de 90˚. A 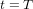 , les particules reviennent pour la deuxième fois à la position initiale.
, les particules reviennent pour la deuxième fois à la position initiale.

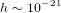 . Pour un détecteur avec une longueur
. Pour un détecteur avec une longueur 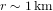 , cela correspond à une variation de longueur de l’ordre de
, cela correspond à une variation de longueur de l’ordre de 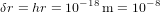 angström, où 1 angström est la taille caractéristique d’un atome. Mesurer une variation de longueur de cette taille correspond à mesurer une fluctuation de l’épaisseur d’un cheveu dans la distance entre le Soleil est l’étoile la plus proche, Proxima du Centaure. Des mesures d’une telle précision semblent impossibles. En fait, elles constituent un défi technologique majeur, mais elles ont été faites.
angström, où 1 angström est la taille caractéristique d’un atome. Mesurer une variation de longueur de cette taille correspond à mesurer une fluctuation de l’épaisseur d’un cheveu dans la distance entre le Soleil est l’étoile la plus proche, Proxima du Centaure. Des mesures d’une telle précision semblent impossibles. En fait, elles constituent un défi technologique majeur, mais elles ont été faites.

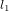 et
et 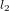 (Fig. 1).
(Fig. 1).
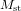 . Une partie de la lumière est réfléchie et redirigée vers le miroir
. Une partie de la lumière est réfléchie et redirigée vers le miroir 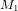 . Une autre partie continue son chemin en ligne droite vers le miroir
. Une autre partie continue son chemin en ligne droite vers le miroir 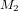 . La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers
. La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers 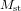 . Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers
. Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers 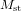 . Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.
. Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.

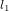 et
et 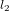 des deux chemins après leur séparation sont
des deux chemins après leur séparation sont 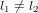 . Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins
. Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins 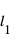 et
et 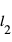 est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (
est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (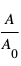 est le rapport entre l’amplitude
est le rapport entre l’amplitude 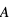 mesurée par le détecteur et l’amplitude
mesurée par le détecteur et l’amplitude 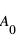 émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin
émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin 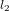 (5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
(5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
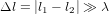 , où
, où  est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si
est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si 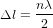 et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si
et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si 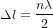 et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.
et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.

