Le champ électrique

Auteur: Andrea Cattaneo

Définition et utilité de la notion de champ électrique

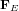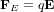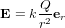La force électrique ${\bf F}_E$ peut être réécrite comme ${\bf F}_E=q{\bf E}$ , où ${\bf E} = k{Q\over r^2}{\bf e}_r$ est le champ électrique.

L’avantage d'introduire ce concept est que le champ électrique 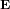${\bf E}$ ne dépend que de la charge Q qui génère le champ et de la position par rapport à elle. Différemment de la force électrique 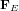${\bf F}_E$ , le champ électrique 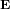${\bf E}$ ne dépend pas de la charge d’essai q qui en subit les effets.

A cette étape de notre exposé (qui suit le développement historique de notre compréhension en la matière), un champ n’est qu’un concept mathématique utilisé pour décrire une quantité (dans le cas du champ électrique, le vecteur 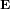${\bf E}$ ) définie en chaque point de l’espace.

Lignes de force du champs électrique

De la même manière que nous avons tracé la force 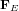${\bf F}_E$ pour différentes positions de la charge q, nous pouvons tracer les lignes de force pour le champ électrique 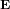${\bf E}$ , qui donnent sa direction en chaque point de l’espace.

La figure ci-dessous montre les ligne de forces pour : a) une charge isolée positive ; b) un système composé par deux charges égales en valeur absolue mais de signes opposés. Cette figure utilise la couleur bleue pour les charges positives et la couleur rouge pour les charges négatives.

Les lignes de forces sortent des charges positives et rentrent dans les charges négatives. Les charges sont donc les sources du champ électrique, où les lignes de force commencent et se terminent. Le champ électrique est plus intense où les lignes de force sont plus denses, c'est-à-dire plus proches les unes des autres.

Une région d’espace vide, comme celle enfermée par la surface S dans la figure ci-dessus, peut contenir des lignes des forces, mais elle ne peut contenir aucun point à partir duquel les lignes de force divergent ou vers lequel les lignes de force convergent.