Principe théorique

Auteur: Andrea Cattaneo

Les ondes gravitaionnelles comme perturbations de l'espace-temps

Concrètement, une onde gravitationnelle est une oscillation dans les valeurs des termes 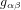$g_{\alpha\beta}$ qui définissent la métrique.

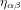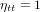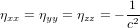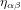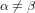Nous ne vivons pas à proximité d’un trou noir. Le champ gravitationnel dont nous faisons l'expérience sur Terre est relativement faible, voilà pourquoi la métrique est très proche de la métrique Minkowski $\eta_{\alpha\beta}$ , pour laquelle $\eta_{tt}=1$ , $\eta_{xx}=\eta_{yy}=\eta_{zz}=-{1\over c^2}$ et $\eta_{\alpha\beta}$ quand $\alpha\ne\beta$ . La personne qui a failli recevoir un pot de fleurs sur la tête ne partagera bien sûr pas cet avis, mais c’est la raison pour laquelle l’amplitude des ondes gravitationnelles est donnée par la matrice :

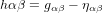$h{\alpha\beta}=g_{\alpha\beta}-\eta_{\alpha\beta}$ (1),

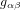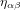qui quantifie la différence entre la vraie métrique $g_{\alpha\beta}$ et la métrique de Minkowski $\eta_{\alpha\beta}$ .

En physique, une perturbation est une petite fluctuation d'une quantité autour d'une valeur de base. L'équation (1) nous montre que 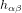$h_{\alpha\beta}$ correspond donc à une perturbation de la métrique.

Effet sur la matière

Pour comprendre comment l’on peut détecter une onde gravitationnelle, il faut se demander qu’est-ce qui se passe pour la matière quand l’amplitude caractéristique h des termes non nuls de la matrice 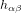$h_{\alpha\beta}$ oscille autour de sa valeur normale, h=0 .

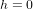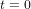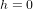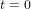Considérons donc le cadran d’une montre imaginaire et huit particules disposées à 1h30, 3h, 4h30, 6h, 7h30, 9h, 10h30 et 12h (Figure ci-dessous). Soit r le rayon du cercle qui passe par les huit particules. Les positions des huit particules sont perturbées par le passage d’une onde gravitationnelle sinusoïdale avec une période T. Nous choisissons le temps t=0 de telle manière que h=0 pour t=0 . A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.

A 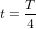$t={T\over 4}$ , h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :

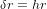$\delta r = hr$ (1).

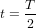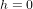A $t = {T\over 2}$ , h=0 . Donc, les particules sont revenues à la position initiale. A 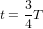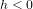$t={3\over 4}T$ , h<0 , donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à 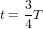$t={3\over 4}T$ a la même forme que l’ellipse à 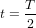$t = {T\over 2}$ tournée de 90˚. A 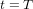t=T , les particules reviennent pour la deuxième fois à la position initiale.

L’effet du passage de l’onde gravitationnelle est donc celui de générer une vibration de la structure de l’espace-temps qui met en oscillation toutes les longueurs.