| La gravité comme force à distance | Les forces électromagnétiques | Nature de la gravité | Les ondes gravitationnelles : propagation | Ondes gravitationnelles : génération | Les ondes gravitationnelles : détection |
Méthode expérimentale |
Le problème auquel on est confronté quand on essaie de détecter les ondes gravitationnelles produites par la coalescence d’un système binaire de trous noirs est que l’amplitude du signal que l’on attend est de l’ordre de 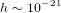 . Pour un détecteur avec une longueur
. Pour un détecteur avec une longueur 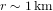 , cela correspond à une variation de longueur de l’ordre de
, cela correspond à une variation de longueur de l’ordre de 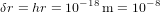 angström, où 1 angström est la taille caractéristique d’un atome. Mesurer une variation de longueur de cette taille correspond à mesurer une fluctuation de l’épaisseur d’un cheveu dans la distance entre le Soleil est l’étoile la plus proche, Proxima du Centaure. Des mesures d’une telle précision semblent impossibles. En fait, elles constituent un défi technologique majeur, mais elles ont été faites.
angström, où 1 angström est la taille caractéristique d’un atome. Mesurer une variation de longueur de cette taille correspond à mesurer une fluctuation de l’épaisseur d’un cheveu dans la distance entre le Soleil est l’étoile la plus proche, Proxima du Centaure. Des mesures d’une telle précision semblent impossibles. En fait, elles constituent un défi technologique majeur, mais elles ont été faites.
L’instrument que l’on utilise pour mesurer des variations de distance très très petites est un interféromètre. La raison de ce nom nous sera claire bientôt. Le principe de fonctionnement d’un interféromètre consiste à utiliser un système de miroirs pour faire arriver un faisceau laser d’une source à un détecteur en lui faisant emprunter deux chemins différents, 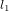 et
et 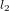 (Fig. 1).
(Fig. 1).
Un faisceau laser sort de la source S, située dans le bâtiment principal, dont les murs sont marqués en jaune. Le faisceau laser rencontre le miroir semi-transparent (la plaque séparatrice de verre semi-argentée) 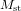 . Une partie de la lumière est réfléchie et redirigée vers le miroir
. Une partie de la lumière est réfléchie et redirigée vers le miroir 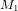 . Une autre partie continue son chemin en ligne droite vers le miroir
. Une autre partie continue son chemin en ligne droite vers le miroir 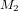 . La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers
. La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers 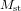 . Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers
. Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers 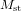 . Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.
. Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.
Les ondes monochromatiques qui arrivent au détecteur par les deux chemins ont été émises avec la même phase, s’agissant du même faisceau laser qui a été séparé en deux, mais elles y arriveront avec des phases différentes si les longueurs 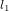 et
et 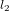 des deux chemins après leur séparation sont
des deux chemins après leur séparation sont 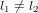 . Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins
. Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins 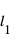 et
et 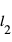 est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (
est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (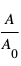 est le rapport entre l’amplitude
est le rapport entre l’amplitude 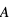 mesurée par le détecteur et l’amplitude
mesurée par le détecteur et l’amplitude 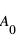 émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin
émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin 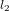 (5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
(5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
En général, 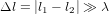 , où
, où  est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si
est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si 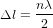 et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si
et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si 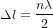 et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.
et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.

Les principaux interféromètres pour la détection d’ondes gravitationnelles sont construits à Hanford (Washington) et Livingstone (Louisiane) par la collaboration américaine LIGO, et à proximité de Pise par la collaboration franco-italienne VIRGO. Un quatrième interféromètre, beaucoup plus petit, a aussi été construit à Hanover par la collaboration anglo-allemande GEO600. D’autres interféromètres seront bientôt opérationnels.
Dans les trois cas, l’interféromètre est constitué d’une unité centrale et de deux bras, qui font 4 km de long dans le cas de LIGO, 3 km de long dans le cas de VIRGO et 600 m de long dans le cas de GEO600. L’unité centrale contient la source laser, le détecteur et la lame séparatrice, un miroir semi-transparent qui sépare la lumière en un faisceau réfléchi et un faisceau transmis. Les deux faisceaux sont envoyés dans les deux bras de l’interféromètre, des tubes sous vide qui se terminent avec des miroirs qui réfléchissent les deux faisceaux vers l’unité centrale. Des systèmes de miroirs sont utilisés afin que la lumière fasse plusieurs aller-retours dans chaque bras avant d’être envoyée au détecteur, de telle manière que tout se passe comme si les bras étaient des centaines de fois plus longs (la vitesse de la lumière est tellement élevée que la lumière peut faire des centaines d’aller-retours dans un temps court par rapport à la période des ondes gravitationnelles, déterminée par la période orbitale des systèmes binaires qui les produisent).
La difficulté la plus grande est due à la présence de nombreuses sources de bruit qui pourraient mettre en vibration les miroirs d’un interféromètre simulant les effet d’une onde gravitationnelle (activité sismique, vent, circulation routière, bruit thermique). La détection d’une onde gravitationnelle avec au moins deux interféromètres à deux endroits différents de la planète est nécessaire pour exclure ces formes de bruits, qui ne peuvent pas générer la même forme d’onde simultanément à plusieurs milliers de kilomètres de distance.