La classification morphologique
E. Hubble proposa en 1926 une
classification des
galaxies selon trois grandes catégories : elliptiques (E),
spirales (barrées SB ou non S) et irrégulières. On y distingue
des sous-classes selon le degré d'ellipticité ou le développement
des bras spiraux des galaxies.
Les galaxies elliptiques
Les galaxies elliptiques ont l'aspect de sphéroïdes plus ou moins aplatis. Elles contiennent une population d'étoiles plutôt vieilles et très peu de gaz ou de poussières. Les galaxies les plus massives sont des galaxies elliptiques, mais il existe aussi une classe de galaxies elliptiques naines, en général
satellites de galaxies plus grosses.
Les galaxies spirales
Les galaxies spirales sont disposées en deux séquences parallèles. Elles contiennent une grande quantité de gaz et de poussières, concentrée dans leur disque, en particulier le long des bras spiraux. On y distingue plusieurs populations d'étoiles d'âges différents, les plus vieilles étant concentrées dans le bulbe central et dans le halo, les plus jeunes étant réparties dans le disque. Les galaxies spirales sont caractérisées morphologiquement par l'importance relative du bulbe, qui décroît du type Sa (ou SBa) vers le type Sc (ou SBc), et le degré d'enroulement des bras autour du noyau. Les bras sont très serrés pour les Sa (ou SBa) et s'ouvrent progressivement jusqu'aux Sc (ou SBc).
Dans les galaxies spirales barrées, le noyau est traversé par une barre d'étoiles, aux extrémités de laquelle débutent les bras spiraux. La présence de gaz et de poussières, de régions ionisées et d'étoiles jeunes s'accroît régulièrement vers les Sc (ou SBc).
Les galaxies irrégulières
Les galaxies irrégulières ont, comme leur nom l'indique, une forme mal définie.
Les galaxies lenticulaires
A la classification de Hubble s'est rajoutée la classe des lenticulaires ou S0. Ce sont des galaxies à très gros bulbe central possédant aussi un disque aplati d'étoiles. Ce disque ne contient pas de bras spiraux, et en général pas ou peu de gaz et de poussières.
Les galaxies naines irrégulières
Enfin, il existe une dernière catégorie, découverte récemment et qui pourrait représenter en nombre presque 50% de la population totale des galaxies, c'est la classe des naines irrégulières. Ce sont des objets à faible brillance de surface, donc difficiles à détecter en optique, mais qui comptent pourtant parfois presque autant d'hydrogène atomique que certaines spirales géantes.
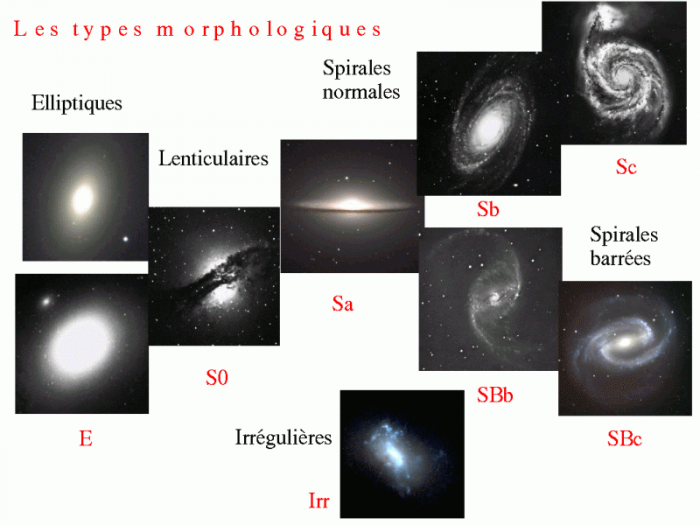
Séquence des types morphologiques des galaxies selon la classification de Hubble
Crédit :
Observatoire de Paris
La relation de Tully-Fisher
La relation de Tully-Fisher relie la magnitude absolue d'une galaxie à sa vitesse de maximale de rotation.
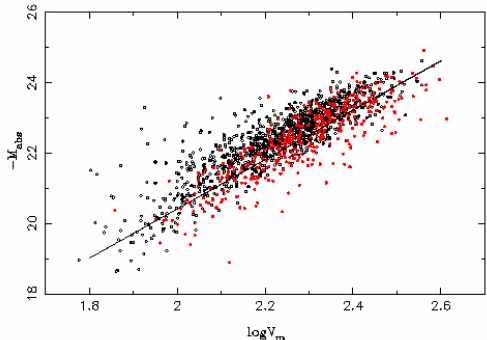
Relation entre la magnitude absolue d'une galaxie et le logarithme de la vitesse de rotation galactique maximale, pour un échantillon de 3000 galaxies de la base de données
LEDA.
Crédit :
ASM
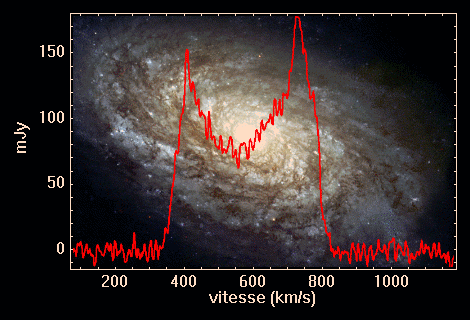
Intensité du profil radio d'une galaxie lointaine (en millijansky, le Jansky représentant
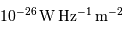
), fonction de la vitesse de rotation mesurée par effet Doppler.
Crédit :
ASM
La relation de Tully-Fisher
La relation de Tully-Fisher, du nom des deux astronomes anglais qui l'ont découverte en 1977, relie la vitesse maximale 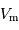 de rotation d'une galaxie spirale à sa luminosité. Cette loi empirique prend la forme suivante :
de rotation d'une galaxie spirale à sa luminosité. Cette loi empirique prend la forme suivante :
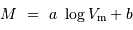
où les coefficients 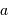 et
et 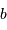 représentent la pente et le point-zéro de la relation. Pour la bande photométrique B, les valeurs acceptées actuellement sont :
représentent la pente et le point-zéro de la relation. Pour la bande photométrique B, les valeurs acceptées actuellement sont :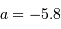 et
et 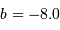 .
.
La mesure du maximum de la vitesse de rotation observée permet alors d'estimer la magnitude absolue, et par comparaison avec l'éclat apparent mesuré, d'en déduire la distance. C'est une relation de type masse-luminosité qui rend compte du fait que, plus une galaxie est massive :
- plus elle tourne vite,
- et plus elle est lumineuse.
La vitesse de rotation est mesurée à partir de l'émission du gaz contenu dans le disque. Cette mesure se fait essentiellement soit à partir d'une courbe de rotation de la galaxie obtenue en spectroscopie optique (analyse de la raie 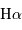 de l'hydrogène en émission), soit à partir du spectre radio
autour de 1420 MHz (analyse de la raie à 21 cm de l'hydrogène neutre). Ce critère permet d'atteindre une précision de 15 à 25 % sur les distances.
de l'hydrogène en émission), soit à partir du spectre radio
autour de 1420 MHz (analyse de la raie à 21 cm de l'hydrogène neutre). Ce critère permet d'atteindre une précision de 15 à 25 % sur les distances.
On obtient un bon étalonnage de la relation Tully-Fisher en utilisant les étoiles céphéides qui ont été observées par le télescope spatial Hubble dans une bonne trentaine de galaxies spirales proches.
Les galaxies sosies
La méthode des galaxies sosies suppose que deux galaxies ayant le même type
morphologique et la même vitesse de rotation ont aussi en moyenne la même luminosité. Il suffit alors de comparer l'éclat observé à l'éclat d'un étalon de distance connue pour avoir la distance de la galaxie. Il n'est pas nécessaire alors de mesurer la pente
de la relation. Il existe aujourd'hui des mesures de vitesse de rotation pour environ 16600 galaxies de notre univers proche.
La relation Faber-Jackson
La relation Faber-Jackson peut comme la précédente être assimilée à un relation
masse-luminosité. Elle relie la luminosité intrinsèque d'une galaxie elliptique ou lenticulaire (mais aussi du bulbe d'une spirale) à la dispersion des vitesses des étoiles mesurées en son coeur. Cette dispersion centrale des vitesses est mesurée à partir de l'élargissement de certaines raies d'absorption dans le spectre optique des galaxies. Ces mesures sont très délicates car il faut pouvoir séparer l'élargissement provenant
des mouvements des étoiles dans la galaxie, de l'élargissement provoqué par la rotation ou les turbulences dans les enveloppes des étoiles elles-mêmes. La relation possède une dispersion relativement
importante d'environ 0.6 magnitude, qui se traduit par une incertitude d'environ 30 % sur les distances estimées. Ce type de mesure est disponible pour environ 4000 galaxies.
Morphologie d'une galaxie spirale
L'appliquette ci-jointe décrit la morphologie d'une galaxie spirale.

Étalonnage de la relation de Tully-Fisher
A l'aide de l'appliquette ci-dessous, on se propose d'étalonner la relation de Tully-Fisher.

- Calculer, à l'aide de l'appliquette, le logarithme décimal de la vitesse exprimée en km/s (se servir de la commande : = log(B))
- Représenter la relation log V - luminosité
- Estimer, à l'aide de l'appliquette, la pente et l'ordonnée à l'origine de la relation
La solution :
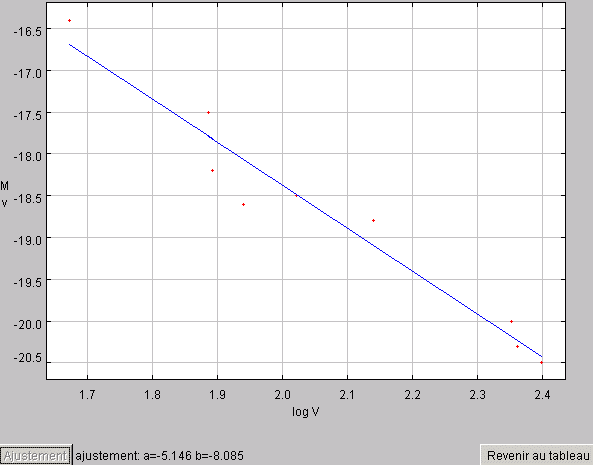
La relation s'exprime :
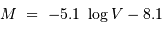
Crédit :
ASM
 Mesure de la largeur de la raie à 21 cm
Mesure de la largeur de la raie à 21 cm
Difficulté : ☆
Temps : 20 min
Mesure de largeur de la raie à 21 cm
| PGC | 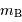 |  (deg) (deg) |
| 49157 | 13.03 | 66.6 |
| 49322 | 15.20 | 67.8 |
| 49275 | 13.34 | 64.1 |
| 48925 | 15.23 | 82.3 |
PGC49157 
PGC49322 
PGC49275 
PGC48925 
Question 1)
Mesurer la largeur de la raie à 21 cm des galaxies PGC 48925, PGC 49157, PGC 49322 et PGC 49275 à partir des spectres disponibles.
La mesure se fait habituellement à 20% de la hauteur de la raie, par rapport à une ligne horizontale passant au milieu du bruit de fond.
Question 2)
Les largeurs de raies sont perturbées par la turbulence  .
En déduire les valeurs
.
En déduire les valeurs 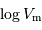 en prenant en compte l'effet de projection et la composante de turbulence de qui élargit la raie. Comparer aux données de la base.
en prenant en compte l'effet de projection et la composante de turbulence de qui élargit la raie. Comparer aux données de la base.
Estimer le rôle de la turbulence sur la raie, ainsi que celui de la projection.
La composante de la turbulence est à soustraire. Le facteur de déprojection est 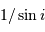 .
.
La largeur totale compte 2 fois la rotation
 Analyse d'un champ extragalactique
Analyse d'un champ extragalactique
Difficulté : ☆☆
Temps : 45 min
Cet exercice repose sur la consultation de divers documents issus de
l'interrogation de la base de données extragalactiques LEDA qui contient les
données de près de 3 millions de galaxies. L'exploration est faite dans une région du ciel au voisinage de la galaxie spirale PGC 49347 (NGC5350)
pour montrer un exemple de recherche de groupement physique de galaxies et un exemple d'application de la relation de Tully-Fisher à un amas.
Les galaxies sont repérées par un numéro PGC (principal galaxy catalog). Les paramètres sont les suivants :
- le type morphologique T : E, SO, Sa-Sm,
- la vitesse radiale héliocentrique en km/s,
- l'inclinaison (calculée à partir du rapport d'axes),
- la magnitude apparente en bande B
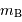 .
.
On dispose d'un tableau des objets répertoriés, classés par ascension droite croissante, et de quatre "zooms" centrés sur quelques galaxies ou groupes intéressants. Dans le tableau, l'inclinaison est donnée en degré, la vitesse radiale en km/s.



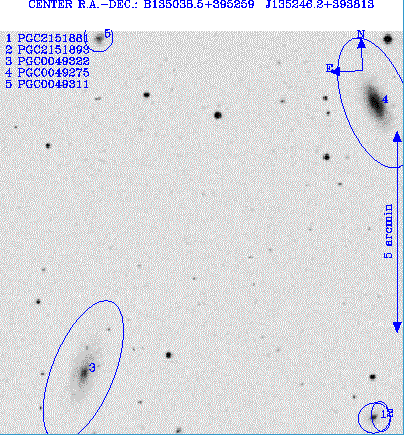
Champ 1 : PGC 49275, 49311, 49322, 2151881, 2151893
Crédit :
LEDA/ASM
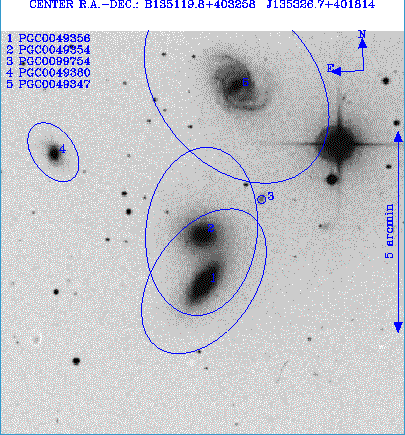
Champ 2 : PGC 49354, 49356, 49347, 49380, 99754
Crédit :
LEDA/ASM

Champ 3 : PGC 49514, 2165372
Crédit :
LEDA/ASM

Champ 4 : PGC 49618, 49624, 2185978
Crédit :
LEDA/ASM
Question 1)
A l'aide des appliquettes, identifier les principales galaxies.
Repérer les différents types morphologiques représentés et les comparer à la table. Identifier la signification des paramètres angulaires pa et i de la table.
Ouvrir le tableau d'une part, l'une des 2 images de l'autre. Y lire les coordonnées des objets.
Les étoiles brillantes, objets ponctuels, sont accompagnées d'une belle figure de diffraction. Ne pas les traiter.
L'unité des paramètres angulaires est visiblement le degré, pa variant de 0 à 180 deg, et i de 0 à 90.
Question 2)
Vérifier que PGC 49354 est presque vue de face, et que PGC 49389 est quasiment vue par la tranche.
Question 3)
Peut-on dire que PGC 49356 et PGC 49389 forment une paire de galaxies ?
Comment reconnaître si elles sont proches selon la dimension radiale perpendiculaire au plan du ciel ?
Question 4)
Comment identifier à partir des divers documents les galaxies formant un petit groupe avec PGC 49347 ?
Le fait d'avoir ces objets sur une même carte indique leur proximité dans le plan du ciel. Comment estimer leur éloignement ?
Question 5)
Rechercher les groupements physiques de galaxies présents dans le
champ. Y a-t-il des galaxies qui sont proches sans être associées ?
 La relation Tully-Fisher et la mesure de H_0
La relation Tully-Fisher et la mesure de H_0
Difficulté : ☆
Temps : 45 min
Cet exercice est basé sur le résultat de l'exercice analysant un champ galactique, c'est à dire de la liste des membres de l'amas principal du champ extragalactique extrait de la base LEDA et centré sur la galaxie PGC 49347 (NGC 5350).
Dans le tableau, l'inclinaison est donnée en degré, la vitesse radiale en km/s.


Question 1)
Expliciter les critères qualitatifs définissant les galaxies utilisables pour appliquer la relation de Tully-Fisher. Peut-on utiliser des galaxies vues quasiment de face ?
Réfléchir aux propriétés que doit avoir la galaxie.
Identifier les données nécessaires.
En ce qui concerne l'inclinaison, quelle mesure doit être possible, et qu'est-ce que cela implique ?
Question 2)
Quantitativement, on fixe pour les critères précédents, une
vitesse radiale dans l'intervalle 2000 - 2600 km/s, une inclinaison
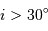 . Sélectionner les galaxies en conséquence.
. Sélectionner les galaxies en conséquence.
Question 3)
Calculer pour chaque galaxie sa magnitude apparente bleue 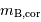 corrigée des effets d'extinction. Le tableau représente les corrections galactique et intergalactique.
Représenter les points
corrigée des effets d'extinction. Le tableau représente les corrections galactique et intergalactique.
Représenter les points 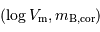 (logvrot, mbc)sur un graphe et évaluer la pente de l'estimation linéaire observée
(logvrot, mbc)sur un graphe et évaluer la pente de l'estimation linéaire observée 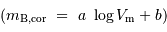 .
.
Dans le tableau, l'inclinaison est donnée en degré, la vitesse radiale (vrad) en km/s, et la vitesse de rotation (logvrot 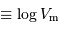 ) en échelle logarithmique, avec également comme unité de vitesse le km/s.
) en échelle logarithmique, avec également comme unité de vitesse le km/s.
Dans quel sens l'extinction agit-elle ?
La correction des effets d'extinction est :
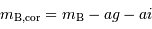 Afficher le graphe de mbc fonction de logvrot, et puis se servir de la fonction ajustement.
Afficher le graphe de mbc fonction de logvrot, et puis se servir de la fonction ajustement.
Question 4)
Calculer l'ordonnée à l'origine 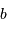 en forçant une pente de -5.8, d'après la pente théorique.
en forçant une pente de -5.8, d'après la pente théorique.
Afficher le graphe de mbc fonction de logvrot, forcer le paramètre a à la valeur -5.8, choisir une valeur pour b et ajuster au mieux "à la main".
Question 5)
Calculer la distance de l'amas en utilisant la relation calibrée en magnitude
absolue : 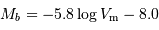
Si besoin, réviser la notion de module de distance.
Question 6)
Estimer la vitesse radiale moyenne 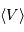 de l'amas et en déduire une valeur de la constante de Hubble
de l'amas et en déduire une valeur de la constante de Hubble 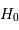 (constante d'expansion).
(constante d'expansion).
Application de la relation de Hubble : 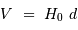
 Galaxies sosie
Galaxies sosie
Difficulté : ☆
Temps : 25 min
Un exercice précédent a permis de repérer les galaxies du groupe de PGC 49347 (NGC 5350).
Question 1)
A l'aide des valeurs tabulées dans les 2 appliquettes de ce précédent exercice, identifier dans les galaxies du groupe de PGC 49347 une galaxie sosie de M31 (galaxie Sb, d'inclinaison 77 deg, de vitesse maximale de rotation 250 km/s), présentant un triplet de paramètres le plus voisin possible. Calculer son module de distance en fonction de celui de M31.
[2 points]
Question 2)
Calculer la distance de cette galaxie sosie, sachant que la magnitude apparente de M31 vaut 3.20 et son module de distance 24.6. En déduire une valeur du taux d'expansion 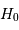 .
.
[2 points]
- Question 1
Aide :
Ouvrir le tableau d'une part, l'une des 2 images de l'autre. Y lire les coordonnées des objets.
Aide :
Les étoiles brillantes, objets ponctuels, sont accompagnées d'une belle figure de diffraction. Ne pas les traiter.
Aide :
L'unité des paramètres angulaires est visiblement le degré, pa variant de 0 à 180 deg, et i de 0 à 90.
Solution :
Les objets caractérisés par une petite valeur de i semblent vus de face ; ceux pour lesquels ce paramètre tend vers 90 deg sont plutôt vus par la tranche : i représente l'inclinaison.
Les objets avec une valeur faible de pa (p.ex. PGC 49514) semblent avoir des axes principaux alignés avec ceux de la carte ; un objet avec
pa de l'ordre de 45 deg (p.ex. PGC 49347) est globalement "en diagonale" par rapport aux axes de position et un autre objet avec
pa de l'ordre de 134 deg (p.ex. PGC 49356) lui est orthogonal : pa représente le paramètre angulaire, à savoir l'orientation des axes.
Les figures des questions suivantes proposent quelques identifications.
- Question 2
Solution :
L'inclinaison de PGC 49354 vaut 23.3 deg ; celle de PGC 49389 vaut 90.0 deg.
- Question 3
Aide :
Comment reconnaître si elles sont proches selon la dimension radiale perpendiculaire au plan du ciel ?
Solution :
Ces galaxies sont proches en ascension droite et déclinaison. Elles doivent également être proches selon la 3e dimension, vu que leurs vitesses de fuite par rapport au Soleil apparaissent très voisines (2300 et 2450 km/s).
- Question 4
Aide :
Le fait d'avoir ces objets sur une même carte indique leur proximité dans le plan du ciel. Comment estimer leur éloignement ?
Solution :
Un groupe d'objets va se caractériser par des vitesses radiales héliocentriques voisines. On repère donc les groupes par leur vitesse radiale. La représenter en fonction de l'une des coordonnées angulaires ou de la magnitude apparente.
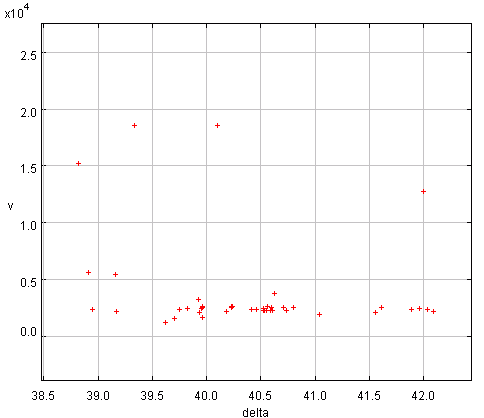
Vitesse héliocentrique fonction de la déclinaison : on repère ainsi un groupe important de galaxies animées d'une vitesse radiale voisine de 2300 km/s.
Crédit :
ASM
- Question 5
Solution :
Avec le critère sur la vitesse radiale héliocentrique, et en représentant cette vitesse en fonction d'une variable angulaire de position ou de la magnitude, on identifie différents groupes :
- amas
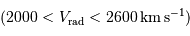 , avec plus de 30 composantes.
, avec plus de 30 composantes. - 2 galaxies avec une vitesse radiale de l'ordre de 5500 km/s.
- 2 galaxies avec une vitesse radiale de l'ordre de 18500 km/s.
- 1 objet avec une bien plus grande vitesse radiale.
- Question 1
Aide :
Réfléchir aux propriétés que doit avoir la galaxie.
Aide :
Identifier les données nécessaires.
Aide :
En ce qui concerne l'inclinaison, quelle mesure doit être possible, et qu'est-ce que cela implique ?
Solution :
Critère sur les objets : il faut sélectionner, parmi la base de données, les galaxies de type spirale, appartenant à l'amas. On exclut donc les irrégulières, celles dont le type n'est pas défini, et celles dont la vitesse radiale est très différente de celle de NGC 5350.
Critère sur les mesures : il faut bien sur que les galaxies possèdent une mesure de 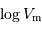 ainsi qu'une magnitude. On exclut celles qui ne satisfont pas à ces critères.
ainsi qu'une magnitude. On exclut celles qui ne satisfont pas à ces critères.
Mesure de la vitesse de rotation : les galaxies ne doivent pas être vues de face afin que la mesure de vitesse de rotation par effet Doppler soit possible.
- Question 2
Solution :
Avec ces critères quantifiés, il ne reste finalement qu'une douzaine d'objets (cf. tableau à la question suivante).
- Question 3
Aide :
Dans quel sens l'extinction agit-elle ?
Aide :
La correction des effets d'extinction est :
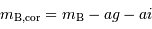 Afficher le graphe de mbc fonction de logvrot, et puis se servir de la fonction ajustement.
Afficher le graphe de mbc fonction de logvrot, et puis se servir de la fonction ajustement.
Solution :
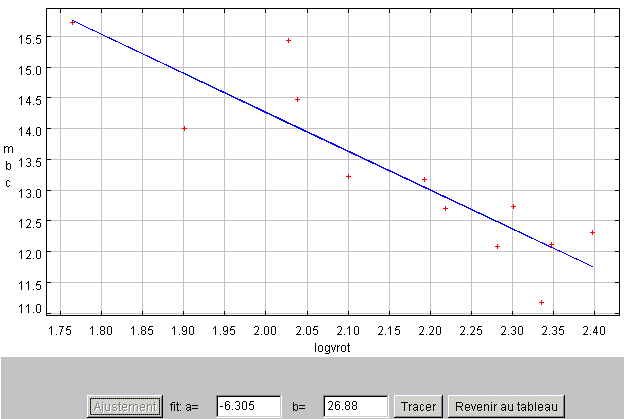
Crédit :
ASM
L'estimation linéaire conduit à une pente de -6.3 et une ordonnée à l'origine de 26.9
- Question 4
Aide :
Afficher le graphe de mbc fonction de logvrot, forcer le paramètre a à la valeur -5.8, choisir une valeur pour b et ajuster au mieux "à la main".
Solution :
Un point apparaît hors norme dans l'estimation (PGC 49480). On l'élimine dans le tableau en remplaçant p.ex. sa magnitude mbc par un blanc. On trouve alors l'estimation avec une pente de -5.83 et une ordonnée à l'origine de 25.7.
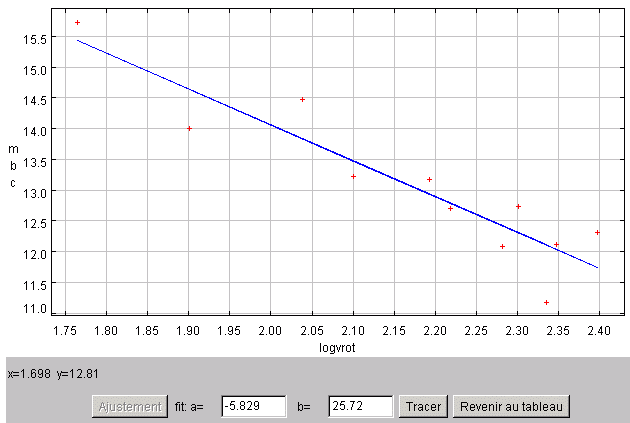
Crédit :
ASM
En forçant la pente à -5.8, le coefficient à l'origine est de l'ordre de 25.6.
- Question 5
Aide :
Si besoin, réviser la notion de module de distance.
Solution :
L'estimation sur les données a conduit à une ordonnée à l'origine de +25.6, pour la magnitude apparente, contre -8 pour la magnitude absolue. Le module de distance vaut donc 33.6. On en déduit, par application de la relation
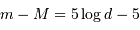 que la distance
que la distance 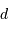 vaut 52 Mpc.
vaut 52 Mpc.
- Question 6
Aide :
Application de la relation de Hubble : 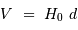
Solution :
La valeur moyenne des vitesses est de l'ordre de 2400 km/s.
L'application de la relation de Hubble 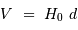 donne
donne 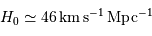 .
.


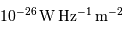 ), fonction de la vitesse de rotation mesurée par effet Doppler.
), fonction de la vitesse de rotation mesurée par effet Doppler.

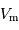 de rotation d'une galaxie spirale à sa luminosité. Cette loi empirique prend la forme suivante :
de rotation d'une galaxie spirale à sa luminosité. Cette loi empirique prend la forme suivante :
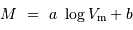
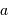 et
et 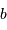 représentent la pente et le point-zéro de la relation. Pour la bande photométrique B, les valeurs acceptées actuellement sont :
représentent la pente et le point-zéro de la relation. Pour la bande photométrique B, les valeurs acceptées actuellement sont :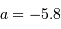 et
et 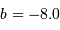 .
.
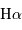 de l'hydrogène en émission), soit à partir du spectre radio
autour de 1420 MHz (analyse de la raie à 21 cm de l'hydrogène neutre). Ce critère permet d'atteindre une précision de 15 à 25 % sur les distances.
de l'hydrogène en émission), soit à partir du spectre radio
autour de 1420 MHz (analyse de la raie à 21 cm de l'hydrogène neutre). Ce critère permet d'atteindre une précision de 15 à 25 % sur les distances.


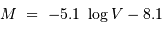
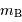
 (deg)
(deg) .
En déduire les valeurs
.
En déduire les valeurs 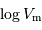 en prenant en compte l'effet de projection et la composante de turbulence de qui élargit la raie. Comparer aux données de la base.
en prenant en compte l'effet de projection et la composante de turbulence de qui élargit la raie. Comparer aux données de la base.
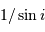 .
.
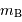 .
.



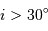 . Sélectionner les galaxies en conséquence.
. Sélectionner les galaxies en conséquence.
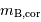 corrigée des effets d'extinction. Le tableau représente les corrections galactique et intergalactique.
Représenter les points
corrigée des effets d'extinction. Le tableau représente les corrections galactique et intergalactique.
Représenter les points 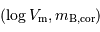
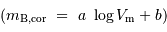 .
.
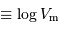 ) en échelle logarithmique, avec également comme unité de vitesse le km/s.
) en échelle logarithmique, avec également comme unité de vitesse le km/s.
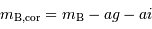 Afficher le graphe de
Afficher le graphe de 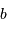 en forçant une pente de -5.8, d'après la pente théorique.
en forçant une pente de -5.8, d'après la pente théorique.
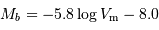
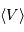 de l'amas et en déduire une valeur de la constante de Hubble
de l'amas et en déduire une valeur de la constante de Hubble 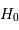 (constante d'expansion).
(constante d'expansion).
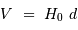
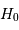 .
.
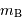
 (deg)
(deg) 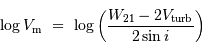
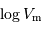 .
.
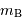
 (deg)
(deg) 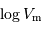

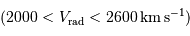 , avec plus de 30 composantes.
, avec plus de 30 composantes.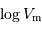 ainsi qu'une magnitude. On exclut celles qui ne satisfont pas à ces critères.
ainsi qu'une magnitude. On exclut celles qui ne satisfont pas à ces critères.


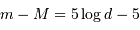 que la distance
que la distance 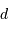 vaut 52 Mpc.
vaut 52 Mpc.
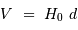 donne
donne 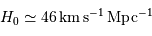 .
.