Associations de lentilles (2)

Auteur: Benjamin Mollier

Lentilles accolées

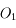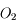Commençons par le cas le plus simple, les deux lentilles accolées. On fait l'hypothèse ici que les deux lentilles sont minces, qu'on les a approchées le plus près possible (que nous permet leur géométrie) de façon à ce qu'on puisse négliger la distance entre les deux centres O_1 et O_2 de celles-ci, devant toutes les grandeurs caractéristiques du système optique. Bref, 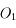O_1 et O_2 sont confondus.

Dans ce cas particulier, notre lentille est équivalente à une seule lentille de vergence

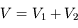
V = V_1+V_2

Autrement dit, sa distance focale image 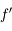peut être déduite par :

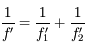
$\frac{1}{f'} = \frac{1}{f'_1} + \frac{1}{f'_2}$

Démonstration

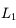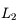Pour vous en convaincre, voici la démonstration. Si on applique la relation de conjugaison de Descartes aux deux lentilles L_1 et L_2 , on obtient :

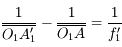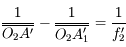
$\frac{1}{\overline{O_1A'_1}} - \frac{1}{\overline{O_1A}} = \frac{1}{f'_1}$ et $\frac{1}{\overline{O_2A'}} - \frac{1}{\overline{O_2A'_1}} = \frac{1}{f'_2}$

Et on en tire donc :

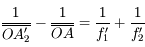
$\frac{1}{\overline{OA'_2}} - \frac{1}{\overline{OA}} = \frac{1}{f'_1} + \frac{1}{f'_2}$

Remarques :

Si la somme des vergences est non nulle, on vient de le voir, nos deux lentilles sont équivalentes à une seule lentille dont la vergence est la somme des deux autres.
Si la somme des vergences est nulle, nos lentilles sont équivalentes à une simple lame de verre. Le grandissement vaut 1. Le système n'a pas de foyer.