La 1ère loi de Kepler
La première loi de Kepler énonce que la trajectoire des planètes est plane. C'est ce que dévoile la trace d'une orbite planétaire, lors d'une révolution sidérale.
La première loi de Kepler énonce que la trajectoire des planètes est plane. C'est ce que dévoile la trace d'une orbite planétaire, lors d'une révolution sidérale.

Référentiels - Notion sur les coniques
Les 3 lois de Kepler expriment les conclusions que Kepler a tirées des observations de Tycho Brahe. Leur caractère empirique -- elles décrivent le mouvement d'une planète autour du soleil, mais ne l'expliquent pas -- n'obère en rien leur portée. Elles ont permis la formalisation par Newton de la loi de gravitation universelle.
Ces lois, obtenues dans le cas particulier du système solaire, se
généralisent à tout système analogue, correspondant à un potentiel
central. L'objet considéré, dans ce potentiel, ayant une masse 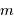 très inférieure à la masse
très inférieure à la masse 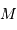 du potentiel central, et n'étant pas perturbé par
d'autres satellites de
du potentiel central, et n'étant pas perturbé par
d'autres satellites de 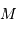 , présente alors les propriétés suivantes :
, présente alors les propriétés suivantes :
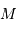 est plane, elliptique, avec
est plane, elliptique, avec 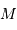 à l'un des
foyers.
à l'un des
foyers.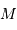 .
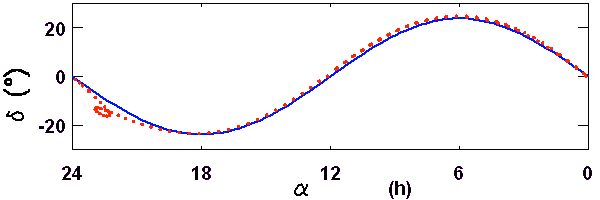
.La 2ème loi de Kepler, ou loi des aires, illustrée dans plusieurs cas.
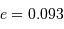
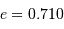
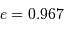
Les différentes "aires balayées" par le rayon vecteur en des durées égales sont égales. Le secteur angulaire correspondant est donc bien plus grand au voisinage du périhélie que de l'aphélie, et cet effet est d'autant plus marqué que l'excentricité de la trajectoire est proche de 1.



La 2ème loi de Kepler permet la détermination de l'équation horaire du mouvement le long de la trajectoire de l'objet.
Les positions des objets (comète de Halley, satellite sur orbite de transfert géostationnaire) sont ici représentées à des dates équiréparties le long d'une période orbitale. Le mouvement est d'autant moins uniforme que l'excentricité de l'orbite est proche de 1 ; la vitesse orbitale est plus rapide au périastre qu'à l'apoastre.



La 3ème loi de Kepler entraîne une période d'autant plus rapide que la planète est proche de l'étoile. L'animation ci-jointe, supposant de manière uniquement illustrative qu'à une date donnée les planètes telluriques pourraient être en phase, montre leur avancée respective au bout d'une durée égale à la période de révolution de Mercure.

Vérifier à l'aide de l'appliquette la 3ème loi de Kepler pour les planètes du système solaire.
On remarque que la validité est moins bonne pour les planètes au-delà de Jupiter, qui ressentent en fait un champ de force moyen de masse totale la masse du Soleil complétée par celle de Jupiter.
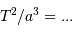
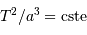 . Et cette constante dépend en fait
. Et cette constante dépend en fait
Difficulté : ☆☆ Temps : 20 min
Cet exercice vous propose une lecture commentée de l'histoire de l'obtention des lois de Kepler. Il se réfère au texte présentant les aspects historiques de l'oeuvre de J. Kepler.
Pourquoi 6 planètes seulement sont-elles citées ? Les identifier.
Que signifie "traduire correctement le mouvement orbital de la Terre" à l'époque de Kepler?
Que représentent 8' (8 minutes d'angle) dans le ciel ? Traduire cette distance angulaire en : fraction du diamètre lunaire, diamètre martien maximal, longueur rapportée sur l'orbite martienne, durée de parcours sur l'orbite martienne. On donne :
Difficulté : ☆☆ Temps : 20 min
Préciser les conditions dans lesquelles les lois de Kepler s'appliquent.
[1 points]
Que représente et signifie le terme "constante", dans l'équation
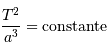
qui traduit la 3ème loi de Kepler.
[1 points]
A quelle(s) condition(s) pourrait-on appliquer les lois de Kepler à une étoile au sein d'un amas stellaire ?
[1 points]
pages_enonce-loi-kepler/enonce-loi-kepler-sexercer.html
pages_lois-kepler/enonce-loi-kepler-sexercer.html
Lesquelles étaient connues en l'an 1600 ?
De Mercure à Saturne, on compte 6 planètes, Terre incluse. Kepler, suivant l'option de Copernic, compte la Terre comme planète : c'est une forte opinion héliocentrique.
Introduire la notion de référentiel.
Il s'agit de choisir le référentiel héliocentrique comme référentiel d'étude, afin de pouvoir proprement corriger tout mouvement du mouvement relatif de la Terre autour du Soleil.
Le diamètre lunaire couvre environ 1/2 degré.
L'erreur de 8', rapportée au diamètre de la Lune de l'ordre de 30', en représente un petit quart.
Le diamètre angulaire maximal de Mars est donné par le rapport de son diamètre linéaire à la distance minimale Terre-Mars, de l'ordre de 0.5 UA (parfois moins, en raison de l'excentricité de l'orbite martienne) :
Le diamètre angulaire, donné par le rapport du diamètre linéaire à la distance considérée, vaut :
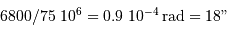 .
.
Il est à comparer à 8' = 480" ; 8' représentent 26.5 diamètres angulaires martiens.
La distance linéaire sur l'orbite est donc de 26.5 diamètres linéaires martiens, soit 180 000 km.
La fraction de l'orbite correspondante s'élève à 8' / 360.60' = 1/2700.
Elle est parcourue en 687 j/2700 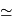 0.25 j, soit 6 heures.
0.25 j, soit 6 heures.