Trajectoire et mouvement

Observer

Le mouvement d'Eugénie
movie.gif
Le satellite de l'astéroïde Eugénie, observé en optique adaptative, à 5 dates différentes.
Crédit : CFHT
Reconstruction d'une trajectoire cométaire
carteikeya.jpg
Reconstruction de l'orbite de la comète Ikeya-Zhang
Crédit : Planétarium de Saint-Etienne

Les trajectoires du système à 2 corps

Exemples de trajectoires dans le système à 2 corps.

Apprendre

objectifsObjectifs

Retrouver rapidement les différentes trajectoires possibles dans un potentiel gravitationnel, en analysant le mouvement radial d'une particule test.

L'écriture explicite de la trajectoire est établie en exercice.

Lois de conservation

Dans un potentiel gravitationnel de masse 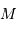M, un objet de masse 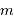m garde une énergie mécanique 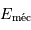E _{\mathrm{m\acute ec}} constante, somme des énergies cinétique et potentielle, égale à :

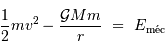
{1\over 2} mv^2 - { {\mathcal{G}} M m\over r} \ = \ E _{\mathrm{m\acute ec}}

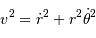En coordonnées polaires, le carré de la vitesse s'écrit : v^2 = \dot r^2 + r^2\dot\theta^2.

Par ailleurs, la conservation du moment cinétique s'énonce :

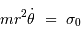
mr^2 \dot\theta \ = \ \sigma_0

Et la vitesse angulaire 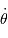\dot\theta s'exprime donc en fonction de l'invariant 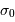\sigma_0 et de la variable radiale 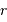r par :

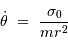
\dot\theta \ = \ {\sigma_0 \over mr^2 }

Le potentiel effectif
poteff0.png
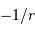Le potentiel effectif est la somme du terme gravitationnel, attractif en -1/r, et du terme rotationnel, répulsif en 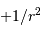+1/r^2. Dès lors que le moment cinétique est non nul, la barrière de moment cinétique empêche d'approcher du centre de force.
Crédit : ASM
Excursion radiale
poteff.png
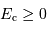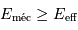Les seules positions radiales accessibles sont celles pour lesquelles E _{\mathrm{c}} \ge 0, càd E _{\mathrm{m\acute ec}} \ge E _{\mathrm{eff}}.
Crédit : ASM
Différentes orbites possibles
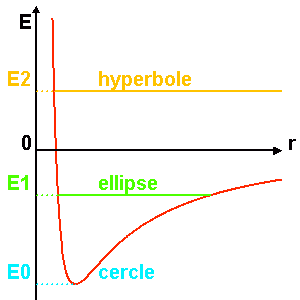
potef.png
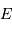Selon la valeur de l'énergie mécanique E, la trajectoire peut être liée (cercle ou ellipse) ou libre (parabole ou hyperbole).
Crédit : ASM

Le potentiel effectif

En éliminant la variable angulaire de l'équation de conservation de l'énergie, on aboutit à une équation reliant l'énergie cinétique radiale 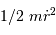1/2 \ m\dot r^2 à un potentiel uniquement radial :

{1\over 2} m\dot r^2 + \left[{ -{ {\mathcal{G}} M m\over r} + {\sigma_0^2\over 2m r^2} }\right] \ = \ E _{\mathrm{m\acute ec}}

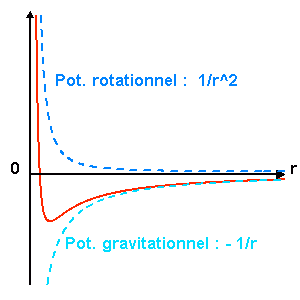
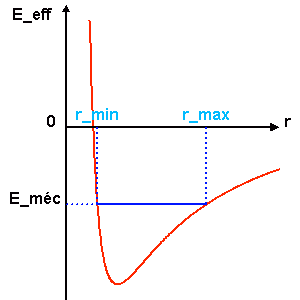
On décide alors d'étudier le mouvement radial du système muni de l'énergie potentielle effective :

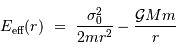
E _{\mathrm{eff}} (r)\ = \ {\sigma_0^2\over 2m r^2}- { {\mathcal{G}} Mm \over r}

On identifie la somme de 2 contributions :

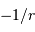
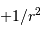
Le mouvement radial s'étudie alors à l'aide de la courbe de potentiel effectif. Les différentes excursions radiales dépendent de l'énergie 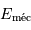E _{\mathrm{m\acute ec}} du système.