
|
Difficulté : ☆☆☆ Temps : 40 min
Une façon très performante de faire de la physique consiste à associer à une loi physique un invariant.
Pour une particule dans un champ de force gravitationnel, le champ de force étant à circulation conservative (voir la signification de ces termes dans le cours de physique), l'énergie mécanique se conserve ; la force étant centrale, le moment cinétique se conserve.
Le but de cet exercice est de montrer
quel invariant est associé au fait que le module de la force
gravitationnel varie comme l'inverse du carré de la distance. Il permet
par ailleurs de retrouver l'équation de la trajectoire elliptique d'un
satellite dans un champ de force central, moyennant un peu de
gymnastique calculatoire.
On considère un satellite, de masse 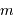 , dans le champ de force central d'un corps de
masse
, dans le champ de force central d'un corps de
masse 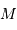 . On repère sa
position par le vecteur radial
. On repère sa
position par le vecteur radial 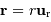 . On note
. On note 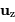 le vecteur
orthonormé normal au plan de la trajectoire, et portant le moment
cinétique du satellite, tel que le trièdre
le vecteur
orthonormé normal au plan de la trajectoire, et portant le moment
cinétique du satellite, tel que le trièdre 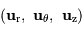 forme
un trièdre orthonomé direct.
forme
un trièdre orthonomé direct.
Exprimer les vecteurs accélération 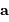 et moment cinétique
et moment cinétique 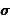 dans la
base (
dans la
base (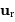 ,
, 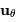 ,
, 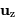 ).
).
On construit le produit vectoriel 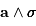 . Donner son expression
en fonction du vecteur
. Donner son expression
en fonction du vecteur 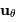 .
.
On multiplie scalairement l'équation précédemment obtenue
par le vecteur position 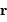 .
Montrer que ceci permet de retrouver l'équation de la trajectoire
.
Montrer que ceci permet de retrouver l'équation de la trajectoire
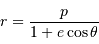
en choisissant pour origine de la variable angulaire 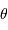 la
direction et le sens du vecteur
excentricité
la
direction et le sens du vecteur
excentricité 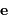
Faire un schéma, représentant le vecteur excentricité 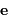 et la
trajectoire.
et la
trajectoire.