
|
Si, historiquement, les lois de Newton ont été dérivées des lois de Kepler, on retrouve aujourd'hui les lois de Kepler comme application des lois de Newton.
L'examen des masses des principaux objets du système solaire dévoile un poids lourd, le soleil, entouré d'un cortèges de petits objets, les planètes. Ceci définit le cadre des approximations usuellement faites pour décrire le mouvement d'une planète : on la considère de masse négligeable par rapport à la masse du soleil, et l'on néglige les interactions interplanétaires.
Le problème se résume à l'interaction entre 2 corps, le soleil de masse
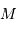 et la planète de masse
et la planète de masse 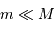 . Le référentiel d'étude
est héliocentrique, de centre
. Le référentiel d'étude
est héliocentrique, de centre 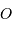 . On y repère la planète
. On y repère la planète 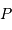 par le
rayon vecteur
par le
rayon vecteur 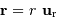 .
La planète subit de la part du soleil une force
.
La planète subit de la part du soleil une force 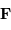 , exprimée par :
, exprimée par :
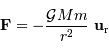
L'étude complète du mouvement est un peu technique. La résolution par les formules de Binet ne sera pas menée dans ce cours ; un autre mode de résolution, introduisant le vecteur excentricité, est proposé en exercice.
La relation fondamentale de la dynamique permet de retrouver que la
trajectoire est plane. Si l'on note 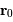 et
et 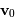 les
position et vitesse de la planète à un instant donné, et
les
position et vitesse de la planète à un instant donné, et 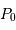 le plan
défini par ces 2 vecteurs, la relation annonce que l'accélération
le plan
défini par ces 2 vecteurs, la relation annonce que l'accélération 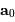 , colinéaire à
, colinéaire à 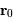 , est également dans ce plan. Aucun terme
d'accélération ne conduisant hors de ce plan, toute la trajectoire s'y
inscrit nécessairement.
, est également dans ce plan. Aucun terme
d'accélération ne conduisant hors de ce plan, toute la trajectoire s'y
inscrit nécessairement.
Comme il suffit que la force soit centrale pour que le moment cinétique du système soit conservé, la dérivation de la 2ème loi de Kepler est immédiate.
On retrouve enfin facilement la 3ème loi de Kepler dans le cas particulier d'un trajectoire circulaire. La démonstration en proposée en exercice.