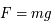Universel ?
Que signifie universel dans l'expression gravitation universelle ?
Que la loi semble s'appliquer à toute échelle dans l'Univers, de la pomme de Newton à la Lune et aux systèmes les plus lointains.
Aujourd'hui, on ne dirait plus universelle, mais unifiée.
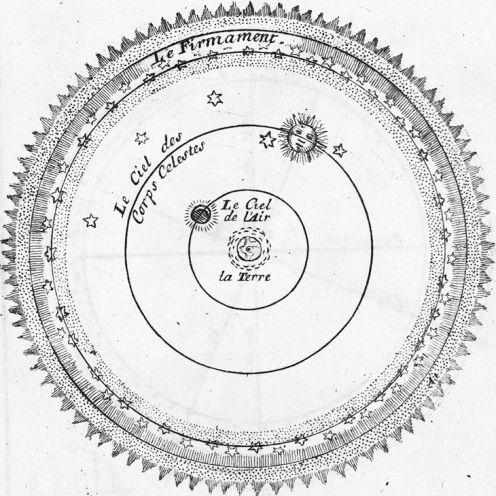
Avant que la gravitation soit universelle.
Crédit :
Bibliothèque de l'Observatoire de Paris
 Prérequis
Prérequis
Relation fondamentale de la dynamique ; notion de référentiel galiléen
La force d'interaction gravitationnelle
Le potentiel gravitationnel
Un objet sphérique de masse 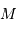 , rayon
, rayon 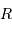 , crée un potentiel gravitationnel :
, crée un potentiel gravitationnel :
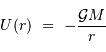
Cette expression suppose implicitement un potentiel nul à
l'infini.
Cette convention, arbitraire comme toute convention, peut se justifier
par divers arguments :
- Le modèle suppose l'absence de toute masse perturbatrice à proximité.
- L'histoire des corps condensés de l'Univers débute dans un
état de matière très dilué, tellement plus dilué que l'état condensé
final que l'on peut considérer les constituants initialement à l'infini,
càd
très éloignés les uns des autres.
- Argument a posteriori : on peut ainsi distinguer un système gravitationnellement lié par son énergie mécanique totale négative. Séparer le système nécessite de lui apporter une énergie qui contrebalance cette énergie de liaison
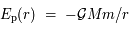
Invariants
Il est commode de traduire les spécificités d'un problème physique en
termes de grandeurs invariantes.
- Champ de force : L'interaction gravitationnelle correspond,
comme toute interaction fondamentale, à un
champ de force. A ce champ de force est associé un potentiel. La
conservation de l'énergie mécanique en découle.
- Force centrale : Le moment d'une force centrale est nul au
centre de force. La conservation du moment cinétique en découle.
- Champ de force central variant comme l'inverse du carré de la distance : Cette forme spécifique du champ de
force introduit un 3e invariant, le vecteur excentricité, qui définit la
trajectoire. Un exercice explicite ceci.
On peut ajouter un autre invariant, pour un système supposé isolé, la conservation de la
quantité de mouvement totale du système.

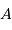 et
et 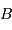 de masse
de masse 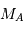 et
et 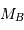 , séparés par la distance
, séparés par la distance 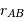 :
:
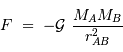
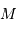 , rayon
, rayon 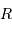 , crée un potentiel gravitationnel :
, crée un potentiel gravitationnel :
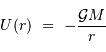
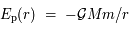
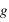 dérive du potentiel gravitationnel
dérive du potentiel gravitationnel 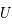 via
via 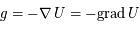 , où l'opérateur gradient désigné la dérivation par rapport à l'ensemble des coordonées spatiales. En coordonnées sphérique, dans un problème à symétrie sphérique,
, où l'opérateur gradient désigné la dérivation par rapport à l'ensemble des coordonées spatiales. En coordonnées sphérique, dans un problème à symétrie sphérique, 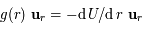
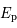 d'un corps de masse
d'un corps de masse 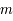 dans un potentiel gravitationnel
dans un potentiel gravitationnel 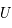 vaut
vaut 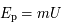
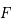 subie par un corps de masse
subie par un corps de masse 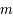 dans un champl gravitationnel
dans un champl gravitationnel 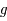 vaut
vaut