 Introduction
Introduction
Prenons n'importe quel système optique, un appareil photo, un télescope, ou même, beaucoup plus simple, une paire de lunettes ou un miroir de salle de bain. Qu'ont en commun tous ces objets ? Regardons de plus près. Ils sont tous constitués de lames de verre, de lentilles et de miroirs. Nous aurons longuement le temps de revenir, dans les chapitres qui suivent, sur les lentilles et sur les miroirs sphériques et paraboliques. Mais, dans un premier temps, nous allons nous intéresser au cas plus simple des miroirs plans, ainsi que de la propagation de la lumière à travers des surfaces planes. De ces premières études, tout le reste découlera naturellement.
Nous avons vu, au chapitre précédent, que la lumière se déplace en ligne droite dans un milieu transparent, homogène et isotrope. Mais que se passe-t-il lorsqu'elle passe d'un milieu THI à un autre ? Continue-t-elle son petit bonhomme de chemin comme si de rien n'était ? Change-t-elle de trajectoire ? ou est-elle même réfléchie ? Des lois simples décrivent le comportement des rayons lumineux à la traversée d'une surface séparant deux milieux transparents.
 Prérequis
Prérequis
Crayon brisé

Le crayon brisé. Un classique de la réfraction.
Crédit :
B. Mollier
Commençons par quelques définitions.
 Définitions
Définitions
Dioptre : on appelle dioptre la surface de séparation de deux milieux transparents à travers laquelle la lumière peut se réfracter, ou sur laquelle elle peut se réfléchir.
Miroir : on appelle miroir une surface formée d'un dépôt métallique, par exemple de l'argent ou de l'aluminium, déposé sur un support qui n'est pas lui-même traversé par la lumière. Il existe une différence majeure entre les miroirs "de salle de bain" et les miroirs utilisés dans les télescopes. En effet, le dépôt métallique est, dans le premier cas, déposé à l'arrière de la paroi en verre. Le verre protège alors le dépôt de l'usure et de l'oxydation. Cependant, avant et après la réflexion sur le dépôt métallique, la lumière traverse l'épaisseur de verre. Ce procédé ne peut être utilisé en astronomie. La traversée du verre cause des réflexions parasites, une perte de lumière et des aberrations chromatiques. Dans le cas des miroirs de télescope, le métal est donc déposé à l'avant de la paroi en verre. Celui-ci n'est alors plus protégé, obligeant à réaluminer régulièrement le miroir.
Différence entre un miroir de salle de bain et un miroir de télescope
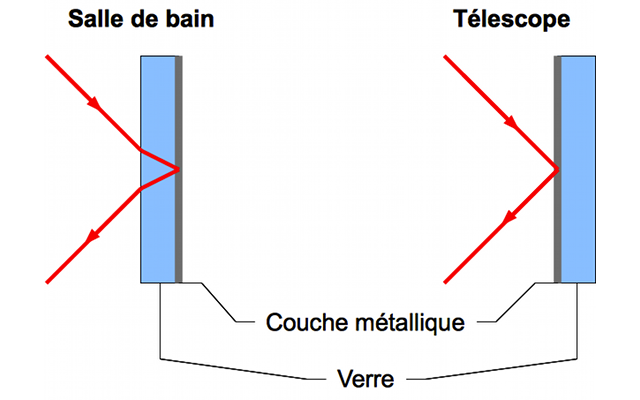
La couche métallique d'un miroir de salle de bain est située derrière le verre, afin de la protéger des rayures, de l'usure et de la corrosion. Elle est placée devant le verre dans un miroir de télescope afin d'éviter l'apparition de réflexions parasites, d'aberrations chromatiques, et de limiter la perte de flux.
Crédit :
ASM/B. Mollier
Point d'incidence : c'est le point de contact 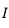 du rayon lumineux incident avec le dioptre ou le miroir.
du rayon lumineux incident avec le dioptre ou le miroir.
Normale au dioptre : il s'agit de l'axe perpendiculaire au dioptre, passant par le point d'incidence.
Plan d'incidence : le plan contenant le rayon incident et la normale au dioptre est appelé plan d'incidence. Notez que ce plan est perpendiculaire au dioptre ou au miroir.
Angle d'incidence : c'est l'angle  entre le rayon incident et la normale au plan.
entre le rayon incident et la normale au plan.
Miroir plan
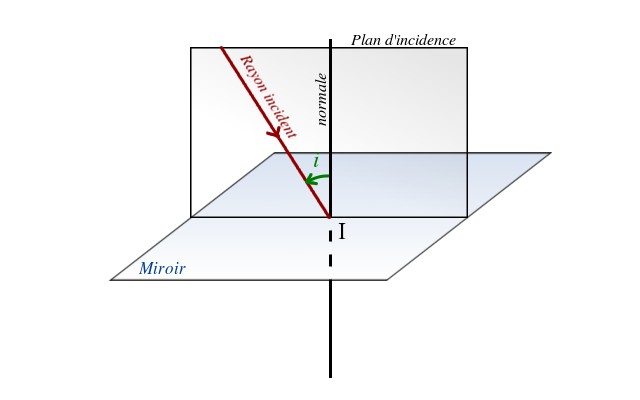
Crédit :
ASM/B. Mollier
Dioptre plan
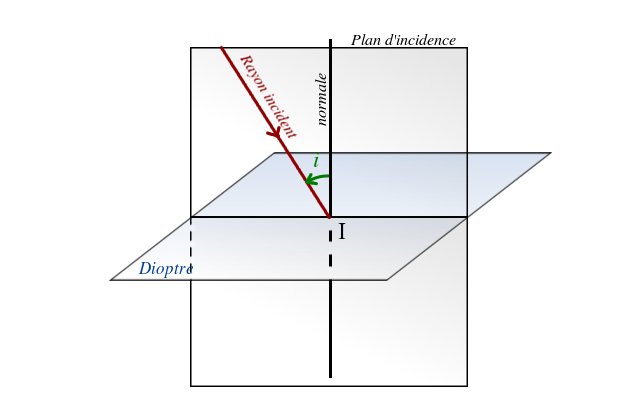
Crédit :
ASM/B. Mollier
 Matériel
Matériel
Nous disposons d'un miroir plan (M) au centre d'un disque gradué. A l'aide d'une source délivrant un mince pinceau lumineux (un laser par exemple), nous éclairons (M) suivant l'axe 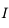 .
.
 Objectif
Objectif
Le but de cette simulation est d'établir une loi liant l'angle incident et l'angle réfléchi.
Soit un rayon lumineux, issu de 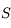 , parvenant au point d'incidence
, parvenant au point d'incidence 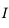 d'un miroir plan parfaitement réfléchissant.
d'un miroir plan parfaitement réfléchissant.
 Lois de la réflexion
Lois de la réflexion
La direction du rayon réfléchi 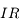 est donnée par la première loi de Descartes :
est donnée par la première loi de Descartes :
- Le rayon
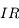 appartient au plan d'incidence
appartient au plan d'incidence - L'angle de réflexion est égal à l'opposé de l'angle d'incidence
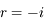
Réflexion sur un miroir plan
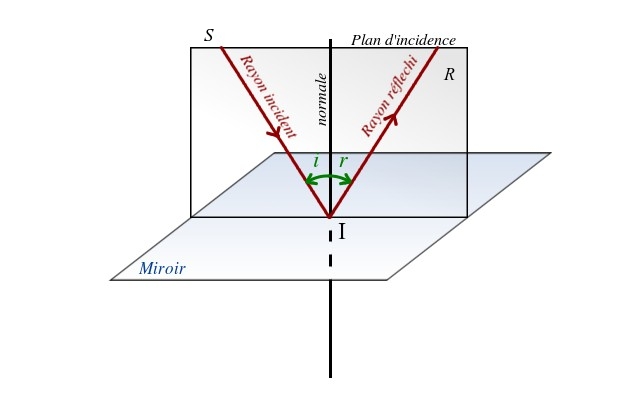
Crédit :
B. Mollier
Auteur: B. Mollier
 Dièdre
Dièdre
Difficulté : ☆
Temps : 5 min
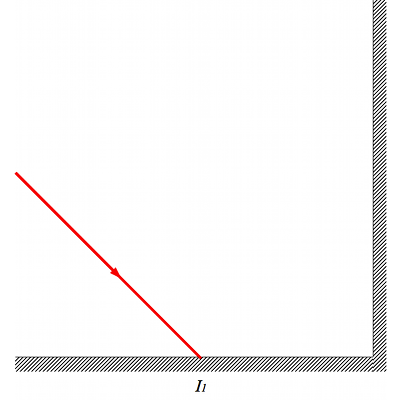
En laboratoire, pour renvoyer la lumière d'où elle vient (c'est-à-dire lui faire faire demi-tour), on utilise un dièdre. C'est un système composé de deux miroirs plans collés l'un à l'autre avec un angle de 90° (voir schéma ci-dessous).
Question 1)
Soit un rayon incident. Tracez le rayon réfléchi par le dièdre.
Dièdre
Crédit :
ASM / B. Mollier
Auteur: B. Mollier
 De l'utilité du dièdre
De l'utilité du dièdre
Difficulté : ☆☆
Temps : 5 min
Nous allons démontrer l'affirmation ci-dessus.
Question 1)
Soit un rayon incident arrivant avec un angle incident 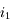 quelconque sur la première face du dièdre. Prouver que, quel que soit la valeur de
quelconque sur la première face du dièdre. Prouver que, quel que soit la valeur de 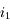 , le rayon réfléchit repartira parallèlement au rayon incident.
, le rayon réfléchit repartira parallèlement au rayon incident.
Montrer que le rayon "tourne" de 180° après les deux réflexions.
Il suffira de montrer que la somme des angles incidents et réfléchis 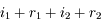 vaut
vaut 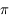
 Objectif
Objectif
Le but de cette simulation est d'établir une loi liant l'angle incident et l'angle réfracté.
Résumons ce que nous venons de constater.
 Simulation
Simulation
Considérons le rayon incident, issu de 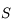 , se propageant dans le MHTI d'indice
, se propageant dans le MHTI d'indice 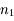 . Au point I appartenant au dioptre, il subit une déviation et une réflexion partielle. Le rayon réfracté se propage dans le MHTI, d'indice
. Au point I appartenant au dioptre, il subit une déviation et une réflexion partielle. Le rayon réfracté se propage dans le MHTI, d'indice 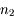 , et le réfléchi, dans le MHTI d'indice
, et le réfléchi, dans le MHTI d'indice 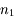 .
.
On énonce ainsi les lois de Snell-Descartes :
Réfraction au passage d'un dioptre
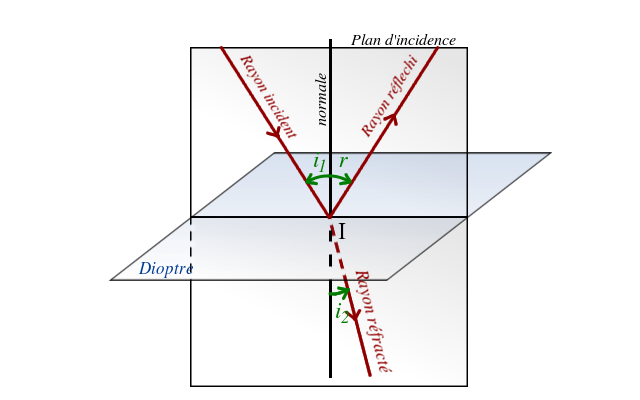
Crédit :
B. Mollier
Conséquences
Le rayon réfracté se rapproche de la normale quand il passe d'un milieu moins réfringent à un milieu plus réfringent. À l'inverse, il s'en éloigne s'il passe d'un milieu plus réfringent à un milieu moins réfringent.
Écartement du rayon en fonction de la réfringence du milieu
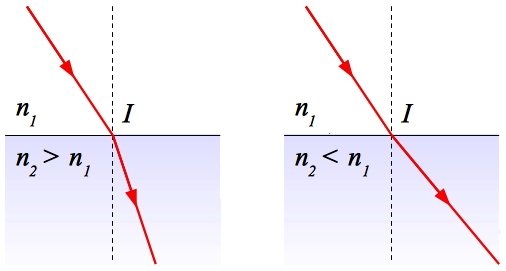
Crédit :
B. Mollier
Nous allons maintenant étudier un cas limite du phénomène de réfraction.
 Simulation
Simulation
Démarrez l'appliquette sur les lois de Snell-Descartes, et placez vous dans le cas où 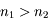 . C'est par exemple le cas lorsqu'un rayon lumineux émerge de l'eau ou du verre pour se retrouver dans l'air.
. C'est par exemple le cas lorsqu'un rayon lumineux émerge de l'eau ou du verre pour se retrouver dans l'air.
 Exercice
Exercice
Augmentez l'angle d'incidence.
Question 1)
Que se passe-t-il ?
Auteur: B. Mollier
 Petits calculs
Petits calculs
Difficulté : ☆
Temps : 10 min
On dispose d'un aquarium et d'un laser.
Question 1)
Le rayon issu du laser arrive avec un angle d'incidence de 50° à la surface de l'eau. Calculer l'angle réfléchi et l'angle réfracté.
L'indice optique de l'air vaut 1. Celui de l'eau 1,33.
Question 2)
On plonge cette fois-ci le laser dans l'eau (oui, il est étanche). L'angle d'incidence est de 35°. Calculez l'angle réfracté avec lequel émerge le rayon laser. Commentez.
 Prisme à réflexion totale
Prisme à réflexion totale
Difficulté : ☆
Temps : 5 min
Dans certains instruments optiques, comme les jumelles par exemple, on utilise un prisme plutôt qu'un miroir, pour réfléchir les rayons lumineux. Ils ont l'avantage de ne pas s'oxyder et d'être plus solides.
Prisme à réflexion totale
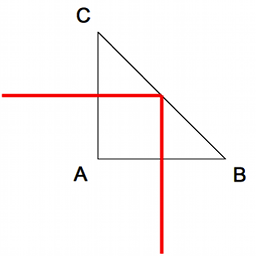
Crédit :
ASM/B. Mollier
Ces prismes possèdent un angle au sommet (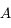 ) de 90°. Le rayon lumineux entre par une petite face (
) de 90°. Le rayon lumineux entre par une petite face (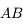 sur le dessin), se réfléchit sur la grande face, ou base
sur le dessin), se réfléchit sur la grande face, ou base 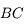 , puis ressort par l'autre face.
, puis ressort par l'autre face.
Question 1)
Calculer l'indice minimal du verre permettant une réflexion totale sur la base.
On prendra la valeur 1 pour l'indice de l'air.
 Un inconvénient du prisme...
Un inconvénient du prisme...
Difficulté : ☆☆
Temps : 15 min
Lorsque le rayon incident arrive perpendiculairement à la face d'entrée, il ressort perpendiculairement à celle de sortie. Il a donc "tourné" de 90°. Mais cela fonctionne-t-il pour n'importe quel angle d'incidence ?
Question 1)
Pas de mystère, la réponse est non. Mais démontrez-le.
 Pentaprisme
Pentaprisme
Difficulté : ☆☆☆
Temps : 45 min
L'inconvénient du prisme précédent est que dès que le rayon lumineux n'arrive plus perpendiculaire à la face d'entrée, l'angle de déviation n'est plus de 90°. Pour garantir un angle de déviation de 90° quel que soit l'angle d'incidence, on utilise un pentaprisme.
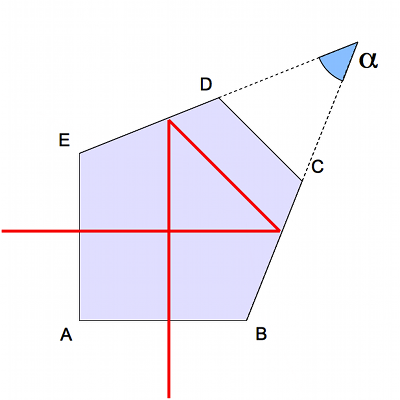
Pentaprisme
Crédit :
ASM/B. Mollier
Utilisation d'un pentaprisme

Utilisation d'un pentaprisme pour l'alignement du banc d'interférométrie FLUOR, situé à l'observatoire du Mont Wilson, en Californie.
Crédit :
E. Lhomé (avec son aimable permission)
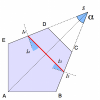
Ce prisme est constitué de 5 faces. Les faces d'entrée et de sortie sont à 90° l'une de l'autre, comme dans le cas précédent. La face où le rayon se réfléchit est remplacée par 3 autres faces. Deux serviront à la réflexion, la dernière n'est pas utilisée. Le prisme est symétrique par rapport à l'axe 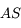 .
.
Question 1)
Calculez la valeur que doit prendre l'angle 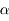 pour garantir une déviation de 90° quel que soit l'angle d'incidence.
pour garantir une déviation de 90° quel que soit l'angle d'incidence.
Pentaprisme
Crédit :
ASM/B. Mollier
Nous avons vu précédemment le phénomène de réflexion totale. Ce phénomène, très intéressant, utilisé dans les jumelles, est à la base des réseaux de communication actuels, car il est utilisé dans les fibres optiques.
 Qu'est-ce qu'une fibre optique ?
Qu'est-ce qu'une fibre optique ?
Une fibre optique peut être vue comme un tuyau de lumière. La lumière se propage dans celle-ci, sans s'échapper. On peut alors transporter de la lumière d'un point A à un point B comme on le ferait avec de l'eau.
Une fibre optique est composé d'un coeur, d'indice 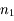 , et d'une gaine, moins réfringente, d'indice
, et d'une gaine, moins réfringente, d'indice 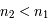 .
.
Le coeur étant plus réfringent que la gaine, une réflexion totale sera possible. Pour que la lumière reste confinée dans le coeur et soit guidée par la fibre, il faut justement se situer dans ce cas de réflexion totale.
 Comment obtenir une réflexion totale ?
Comment obtenir une réflexion totale ?
A l'interface coeur-gaine, on obtient ainsi une condition sur l'angle d'incidence que doit avoir la lumière, pour rester confinée dans le coeur.
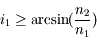
Or, le rayon lumineux vient de l'extérieur. Il subit donc également une réfraction au passage de l'air vers le coeur à son entrée dans la fibre. En appliquant une fois de plus les lois de la réfraction, on obtient :
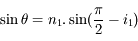 soit
soit 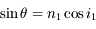 .
.
d'où l'angle limite 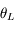 pour que la lumière rentre dans la fibre et soit guidée :
pour que la lumière rentre dans la fibre et soit guidée :
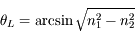
 Simuler
Simuler
Propagation d'un rayon lumineux dans un fibre optique 
Laissons de côté, quelques instants, les calculs, pour faire un peu de dessin. Nous allons tenter de déterminer graphiquement la direction du rayon réfracté, sans employer de rapporteur.
Auteur: B. Mollier
 Une histoire de pièce...
Une histoire de pièce...
Difficulté : ☆☆☆
Temps : 30 min
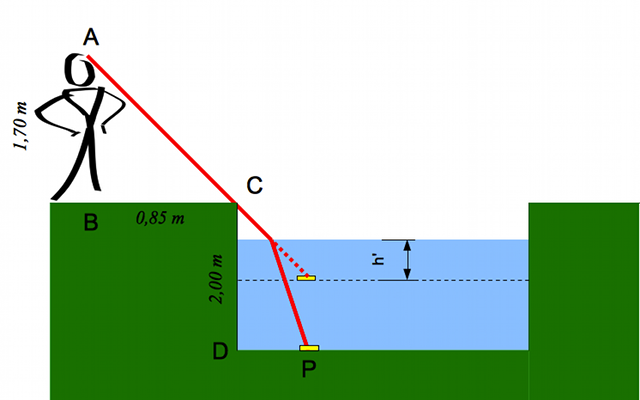
On jette une pièce au fond d'une piscine vide. Cette première se trouve à 80 cm du bord de la seconde. La profondeur de la piscine est de 2 m. Une personne, mesurant 1,70 m se trouve à 85 cm du bord.
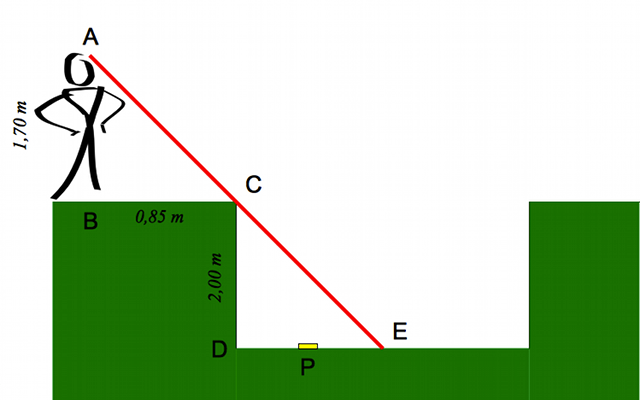
Crédit :
ASM/B. Mollier
Question 1)
Cette personne voit-elle la pièce au fond de la piscine ?
Question 2)
On remplit la piscine d'eau. Quelle doit être sa hauteur minimale pour apercevoir la pièce ?
L'indice optique de l'eau vaut 1,33.
Question 3)
Notre cerveau ne perçoit pas le changement de direction du rayon lumineux. Il a l'impression que celui-ci se déplace toujours en ligne droite. On a donc l'impression de voir la pièce moins profonde qu'elle ne l'est réellement. Quelle est alors la hauteur 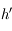 d'eau que l'on a l'impression de voir ?
d'eau que l'on a l'impression de voir ?
Crédit :
ASM/B. Mollier
Nous allons ici abandonner quelques instants le H de MHTI pour étudier des milieux à indice variable.
Nous avons tous déjà observé des phénomènes de mirage optique.
- La fameuse flaque d'eau, que l'on aperçoit sur les routes goudronnées et pourtant sèches en été. Ce n'est que le reflet du ciel sur la route surchauffée.
- En bord de mer, par temps chaud, si la mer est froide, il est parfois possible d'apercevoir une île ou un voilier pourtant situé derrière l'horizon, ou d'en voir deux images l'une au dessus de l'autre.
- En février ou en novembre, il est parfois possible de voir, depuis Marseille, le Soleil se coucher derrière le mont Canigou, alors que celui-ci est normalement invisible. En effet, d'après le principe de propagation rectiligne de la lumière, les rayons issus de cette montagne passeraient à plusieurs dizaines de mètres sous la Méditerranée.
Nous allons voir que tous ces phénomènes impliquent des changements d'indice de l'atmosphère dus à des changements de température. Nous n'aborderons ces phénomènes que de manière qualitative.
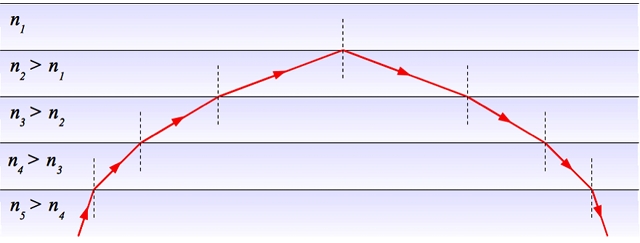
Un milieu d'indice variable peut-être vu comme la superposition d'une multitude de couches de MHTI d'indices différents. Si un rayon se propage des indices les plus grands vers les plus faibles, à chaque passage d'un milieu à un autre, il s'éloigne de la normale jusqu'à être réfléchi puis repartir vers les milieux à fort indice. Il se retrouve ainsi dans la situation inverse, en se rapprochant de plus en plus de la normale.
Indice variable
Crédit :
B. Mollier
 Conclusion
Conclusion
Dans un milieu d'indice variable, le rayon tourne toujours sa courbure vers les indices élevés.
Muni de ce résultat, voyons si nous pouvons expliquer les mirages.
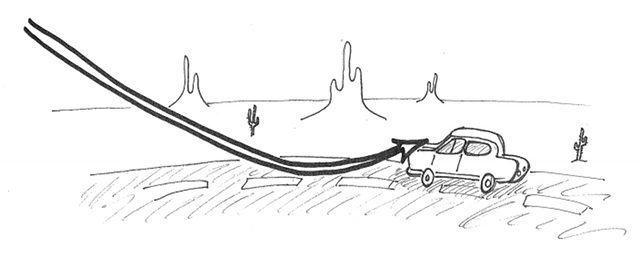
 Sur la route des vacances...
Sur la route des vacances...
En été, la route exposée au Soleil chauffe. Sa température devient plus élevée que celle de l'air environnant. Elle chauffe à son tour l'air ambiant, plus frais. On obtient alors un gradient de température au dessus de la route. La température diminue avec l'altitude, et augmente quand on se rapproche de la route. L'air chaud possède un indice de réfraction plus faible que l'air frais. (On peut voir ça de la manière suivante : pour un même volume, l'air chaud contient moins de particules que l'air froid, c'est pour ça qu'il est plus léger et fait s'envoler les montgolfières. Comme il y a moins de particules, il se rapproche plus du vide et donc son indice tend vers 1). La lumière tourne donc sa courbure vers le haut et les indices élevés. Un rayon issu du ciel se rapproche de la route, est lentement dévié puis finalement réfléchi et repart vers le haut et l'oeil de l'automobiliste. On voit donc le ciel en bas.
Crédit :
B. Mollier
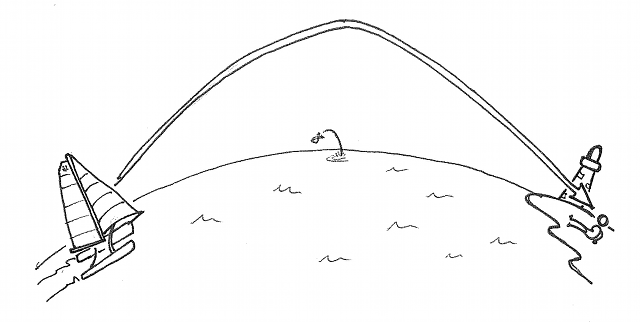
 ... en arrivant à la plage.
... en arrivant à la plage.
Dans le cas de la mer, le phénomène est inverse. La mer plus froide refroidit localement l'air. Il y a un gradient de température du plus froid au niveau de l'eau, au plus chaud en altitude. Un rayon partant d'une île, ou du Canigou, se réfléchit sur l'atmosphère et retombe vers l'observateur. L'île apparaît.
Crédit :
B. Mollier
 Turbulence atmosphérique
Turbulence atmosphérique
Nous venons de le voir, une variation de la température provoque une variation d'indice optique.
Or, lorsque la lumière issue d'une étoile arrive au niveau de la Terre, elle traverse différentes couches d'atmosphère à différentes températures. L'atmosphère est un milieu inhomogène !
Ces variations d'indice dévient les rayons lumineux issus de l'étoile. Mais elles ne les dévient pas de la même manière en fonction de là où ils passent. L'image de l'étoile est déformée !
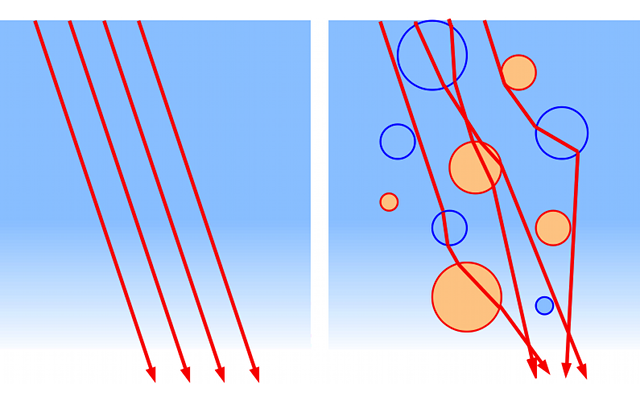
L'atmosphère contient de nombreuses bulles de température et donc d'indice optique différents. Ces bulles se déplacent au gré des vents. Elles dévient aléatoirement les rayons lumineux, provoquant le scintillement des étoiles. C'est la turbulence atmosphérique.
Crédit :
ASM/B. Mollier
À l'oeil, on voit alors les étoiles scintiller. Au télescope, une succession de poses courtes révèle la présence de tavelures, c'est-à-dire plein de taches qui bougent. Toutes ces tavelures sont autant d'images de l'étoile, ayant traversé différentes parties de l'atmosphère.
Tavelures

Tavelures (ou speckles en anglais), enregistrées par lors d'une pose courte (image de gauche, en vidéo inverse) ou longue (image de droite).
Crédit :
ESO
 Déviation
Déviation
Lorsque qu'un rayon lumineux passe d'un milieu moins réfringent à un milieu plus réfringent, il se rapproche de la normale au dioptre.
Lorsque qu'un rayon lumineux passe d'un milieu plus réfringent à un milieu moins réfringent, il s'éloigne de la normale au dioptre. Dans ce cas, à partir d'un certain angle critique, il est totalement réfléchi. Les fibres optiques exploitent ce phénomène appelé réflexion totale.
 Milieux d'indice variables
Milieux d'indice variables
Mirages et turbulences atmosphériques sont dus à des inhomogénéités d'indice dans l'atmosphère, conséquences d'inhomogénéités de température.
- Question 1
Solution :
Nous allons y aller pas à pas. Tout d'abord, au point 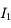 , on a la relation
, on a la relation 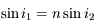 .
.
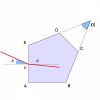
Au point 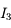 ,
, 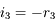 . Exprimons
. Exprimons 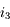 . Dans le triangle
. Dans le triangle 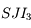 ,
, 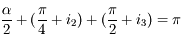 , d'où
, d'où 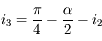
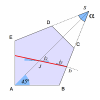
Au point 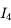 ,
, 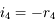 . Exprimons
. Exprimons 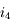 . Dans le triangle
. Dans le triangle 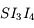 ,
, 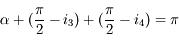 . Donc
. Donc 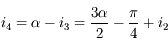 .
.
Enfin, au point 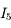 ,
, 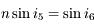 . Exprimons
. Exprimons 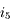 . Dans le triangle
. Dans le triangle 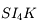 ,
, 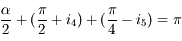 , d'où
, d'où 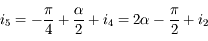
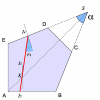
Pour garantir une déviation de 90°, il faut que 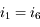 donc
donc 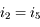 . Cela entraîne que
. Cela entraîne que 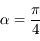
L'angle 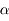 doit donc mesurer 45°
doit donc mesurer 45°
 Introduction
Introduction

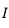 du rayon lumineux incident avec le dioptre ou le miroir.
du rayon lumineux incident avec le dioptre ou le miroir.
 entre le rayon incident et la normale au plan.
entre le rayon incident et la normale au plan.


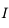 .
.

 et
et 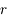 ? Pour le déterminer, cliquez sur "Tracé de rayons et calcul d'angle".
? Pour le déterminer, cliquez sur "Tracé de rayons et calcul d'angle".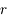 en fonction de
en fonction de  . Faites varier
. Faites varier  .
.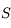 , parvenant au point d'incidence
, parvenant au point d'incidence 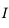 d'un miroir plan parfaitement réfléchissant.
d'un miroir plan parfaitement réfléchissant.
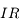 est donnée par la première loi de Descartes :
est donnée par la première loi de Descartes :
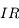 appartient au plan d'incidence
appartient au plan d'incidence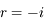


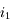 quelconque sur la première face du dièdre. Prouver que, quel que soit la valeur de
quelconque sur la première face du dièdre. Prouver que, quel que soit la valeur de 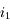 , le rayon réfléchit repartira parallèlement au rayon incident.
, le rayon réfléchit repartira parallèlement au rayon incident.
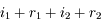 vaut
vaut 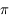
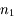 et
et 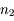 . Un rayon incident issu de
. Un rayon incident issu de 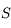 arrive sur le dioptre les séparant en
arrive sur le dioptre les séparant en 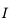 .
.
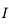 observe-t-on ?
observe-t-on ?
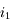 et réfracté
et réfracté 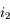 sont-ils égaux ?
sont-ils égaux ?
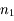 et
et 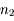 . Un rayon incident issu de
. Un rayon incident issu de 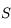 arrive sur le dioptre les séparant en
arrive sur le dioptre les séparant en 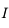 .
.
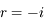
 .
.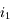 ,
, 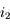 ,
, 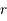 "
"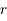 et
et 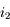 en fonction de
en fonction de 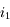
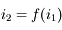 n'est clairement pas linéaire.
n'est clairement pas linéaire.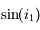 et
et 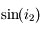
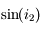 en fonction de
en fonction de 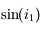
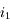 et
et 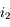 sont petits :
sont petits :
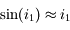
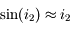
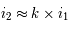
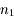 et
et 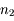 . Un rayon incident issu de
. Un rayon incident issu de 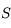 arrive sur le dioptre les séparant en
arrive sur le dioptre les séparant en 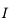 .
.
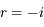
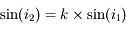
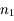 d'abord, puis
d'abord, puis 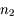 ensuite.
ensuite.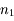 ?
?
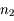 ?
?
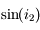 est proportionnel à
est proportionnel à 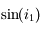 , proportionnel à
, proportionnel à 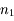 et inversement proportionnel à
et inversement proportionnel à 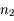 . Sur l'appliquette, calculer la pente de la courbe
. Sur l'appliquette, calculer la pente de la courbe 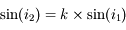 . Comparez-la au rapport
. Comparez-la au rapport 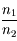 .
.
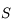 , se propageant dans le MHTI d'indice
, se propageant dans le MHTI d'indice 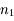 . Au point I appartenant au dioptre, il subit une déviation et une réflexion partielle. Le rayon réfracté se propage dans le MHTI, d'indice
. Au point I appartenant au dioptre, il subit une déviation et une réflexion partielle. Le rayon réfracté se propage dans le MHTI, d'indice 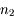 , et le réfléchi, dans le MHTI d'indice
, et le réfléchi, dans le MHTI d'indice 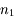 .
.
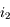 est relié à
est relié à 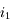 par la relation
par la relation
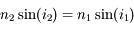
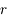 par
par
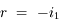


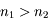 . C'est par exemple le cas lorsqu'un rayon lumineux émerge de l'eau ou du verre pour se retrouver dans l'air.
. C'est par exemple le cas lorsqu'un rayon lumineux émerge de l'eau ou du verre pour se retrouver dans l'air.
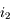 varie de 0 à 90°,
varie de 0 à 90°, 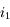 ne varie que de 0 à
ne varie que de 0 à 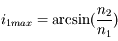 . Tout rayon incident arrivant au niveau du dioptre avec un angle supérieur à celui-ci sera totalement réfléchi. Il ne sera pas réfracté ! C'est ce qu'on appelle le phénomène de réflexion totale. Nous allons le voir, ce phénomène est utilisé dans plusieurs systèmes optiques.
. Tout rayon incident arrivant au niveau du dioptre avec un angle supérieur à celui-ci sera totalement réfléchi. Il ne sera pas réfracté ! C'est ce qu'on appelle le phénomène de réflexion totale. Nous allons le voir, ce phénomène est utilisé dans plusieurs systèmes optiques.

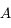 ) de 90°. Le rayon lumineux entre par une petite face (
) de 90°. Le rayon lumineux entre par une petite face (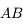 sur le dessin), se réfléchit sur la grande face, ou base
sur le dessin), se réfléchit sur la grande face, ou base 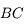 , puis ressort par l'autre face.
, puis ressort par l'autre face.


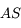 .
.
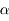 pour garantir une déviation de 90° quel que soit l'angle d'incidence.
pour garantir une déviation de 90° quel que soit l'angle d'incidence.

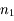 , et d'une gaine, moins réfringente, d'indice
, et d'une gaine, moins réfringente, d'indice 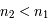 .
.
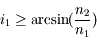
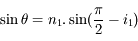 soit
soit 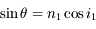 .
.
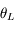 pour que la lumière rentre dans la fibre et soit guidée :
pour que la lumière rentre dans la fibre et soit guidée :
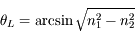
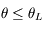 , la lumière sera guidée.
, la lumière sera guidée.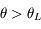 , la lumière ne sera pas guidée.
, la lumière ne sera pas guidée.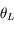 est appelé l'ouverture numérique de la fibre.
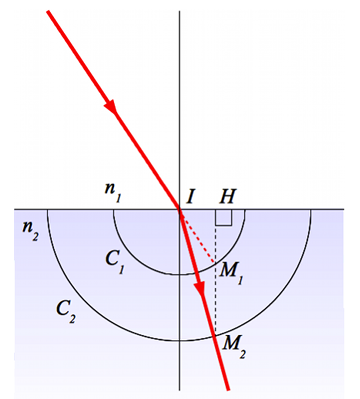
est appelé l'ouverture numérique de la fibre.
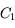 et
et 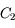 de centre
de centre 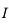 , et de rayon
, et de rayon 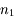 et
et 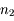 respectivement, repérons l'intersection
respectivement, repérons l'intersection 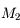 du rayon incident avec le cercle
du rayon incident avec le cercle 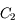 . Soit
. Soit 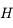 le projeté de
le projeté de 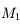 sur le dioptre. On définit
sur le dioptre. On définit 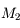 le point d'intersection de la droite
le point d'intersection de la droite 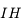 avec le second cercle. Étant donné que
avec le second cercle. Étant donné que 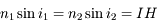 , la droite
, la droite 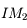 indique la direction du rayon réfracté.
indique la direction du rayon réfracté.

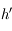 d'eau que l'on a l'impression de voir ?
d'eau que l'on a l'impression de voir ?






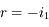 .
.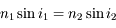 ,
, 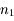 et
et 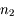 étant les indices optiques des milieux 1 et 2.
étant les indices optiques des milieux 1 et 2.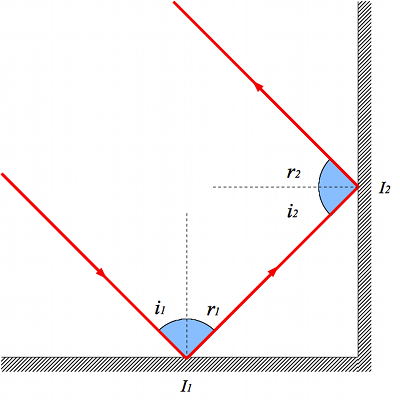
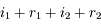 . On sait que
. On sait que 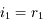 et
et 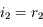 en valeur absolue. Donc cette somme vaut
en valeur absolue. Donc cette somme vaut 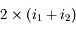 .
.
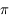 . Donc
. Donc 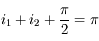 , d'où
, d'où 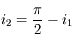
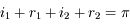 et ce, quel que soit la valeur de
et ce, quel que soit la valeur de 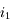 .
.
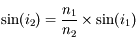
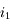 , l'angle réfracté
, l'angle réfracté 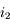 disparaît. Le rayon incident est totalement réfléchi. Il y a réflexion totale !
disparaît. Le rayon incident est totalement réfléchi. Il y a réflexion totale !
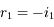
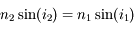
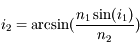 et
et 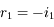
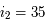 ° et
° et 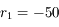 °
°
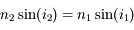 , d'où
, d'où 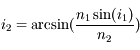
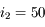 °
°
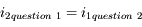 et
et 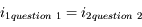 . On vient de vérifier le principe de retour inverse de la lumière.
. On vient de vérifier le principe de retour inverse de la lumière.
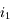 de 45°. Pour qu'il y ait réflexion totale, il faut que l'angle réfracté vaille au minimum 90°. En appliquant les lois de Snell-Descartes
de 45°. Pour qu'il y ait réflexion totale, il faut que l'angle réfracté vaille au minimum 90°. En appliquant les lois de Snell-Descartes
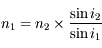
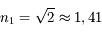
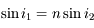 , et sur la face de sortie,
, et sur la face de sortie, 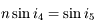
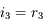 , en valeur absolue. Cela nous garantit, par symétrie de la construction, que
, en valeur absolue. Cela nous garantit, par symétrie de la construction, que 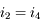 et
et 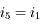 . D'où, l'angle de déviation vaut
. D'où, l'angle de déviation vaut 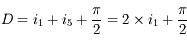
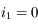 , la déviation est de 90°, sinon, elle ne l'est pas.
, la déviation est de 90°, sinon, elle ne l'est pas.
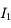 , on a la relation
, on a la relation 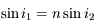 .
.
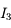 ,
, 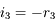 . Exprimons
. Exprimons 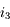 . Dans le triangle
. Dans le triangle 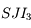 ,
, 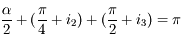 , d'où
, d'où 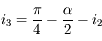
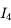 ,
, 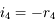 . Exprimons
. Exprimons 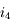 . Dans le triangle
. Dans le triangle 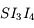 ,
, 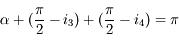 . Donc
. Donc 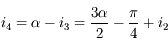 .
.
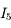 ,
, 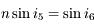 . Exprimons
. Exprimons 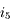 . Dans le triangle
. Dans le triangle 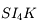 ,
, 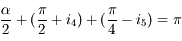 , d'où
, d'où 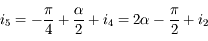
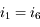 donc
donc 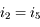 . Cela entraîne que
. Cela entraîne que 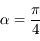
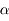 doit donc mesurer 45°
doit donc mesurer 45°
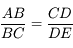 d'où
d'où 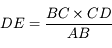
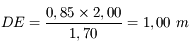
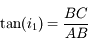 et donc
et donc 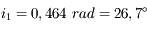 .
. 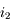 se calcule à partir des lois de Snell-Descartes.
se calcule à partir des lois de Snell-Descartes.
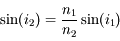
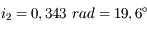 .
.
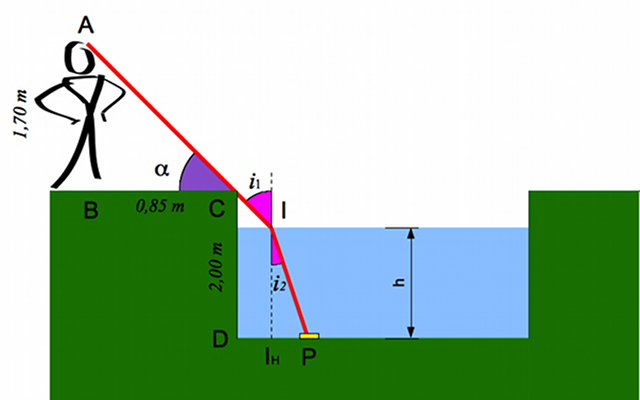
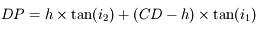
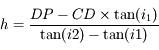
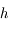 :
:
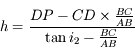
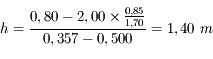
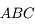 et
et 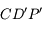 sont semblables, donc
sont semblables, donc
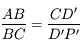
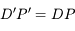 , donc
, donc
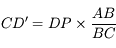
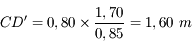
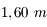 , et donc la hauteur apparente d'eau
, et donc la hauteur apparente d'eau 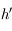 vaut
vaut 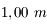 .
.