Mécanique céleste, Temps et Calendriers
Auteur: Jean-Eudes Arlot
- Introduction
- Introduction à la notion de repère
- Introduction
- La voûte céleste
- La sphère locale
- Exercice
- Le mouvement diurne
- Le mouvement annuel
- Les repères, outils mathématiques pour se positionner
- La notion de repère cartésien
- Se positionner dans le plan
- Translation de repère
- Exercice : Calcul de coordonnées polaires dans le plan
- Se positionner dans l'espace
- Exercice : Calcul des coordonnées polaires dans l'espace
- Les unités angulaires
- Exercice : conversion des unités
- Les repères de l'astronomie "fixes"
- Introduction
- Les repères quasi fixes
- Le repère céleste écliptique
- Exercice
- Le repère céleste équatorial
- Changement de repère
- Formulaire de trigonométrie sphérique
- Relations entre les coordonnées polaires écliptiques et équatoriales
- Position du Soleil sur l'écliptique
- Les mouvements du repère équatorial
- La médiation
- Le repère galactique J2000
- Les coordonnées terrestres
- Calcul des coordonnées géocentriques
- Les repères locaux
- Introduction
- Le système de coordonnées équatoriales horaires
- Exercice
- Effet d'un changement de longitude terrestre
- La variation du temps sidéral
- Le repère local
- Quelques définitions supplémentaires
- Formulaires liant les coordonnées locales
- Remarque sur le repère local (alt-azimutal)
- Simulations
- Exercices d'utilisation des simulations
- Applications liées au repère local
- Introduction
- Quelques définitions supplémentaires
- Les astres circumpolaires
- Astres ayant une plus grande digression est et ouest
- Tracer de la sphère locale dans l'hémisphère sud
- Passage au méridien supérieur
- Exercice : Passage au méridien
- Passage d'un astre au méridien inférieur
- Conclusion
- QCM
- Applications liées au repère local-2
- Hauteur du plan équatorial au dessus de l'horizon
- Hauteur du plan équatorial au dessous de l'horizon
- Passage du Soleil au zénith entre les tropiques
- Exercice
- Trouver les limites des étoiles qui ne se lèvent pas
- Trouver les limites des étoiles qui ne se couchent pas
- Trouver les étoiles ayant une plus grande digression
- Distinction entre les étoiles circumpolaires et les étoiles ayant une plus grande digression
- Simulation
- Les nouveaux repères
- Les nouveaux systèmes de reférence
- La mesure des distances
- Introduction
- Comment mesurer une distance en astronomie ?
- La triangulation
- La parallaxe en astronomie
- Exercice
- La mesure par la parallaxe
- En savoir plus: la parallaxe horizontale
- Mesure de la distance Terre-Soleil et Terre-Planètes
- La nécessité d'un modèle théorique en astronomie
- Exercice
- La mesure de la Terre
- Passage d'un angle apparent à une distance
- Exercice
- La distance Terre-Lune
- La mesure de la distance Terre-Lune par les éclipses
- Les lois de Kepler
- Introduction
- L'héliocentrisme
- Pourquoi l'héliocentrisme ?
- Histoire : de la Terre plate aux orbites elliptiques
- Histoire : le monde d'Aristote
- Histoire : les premières mesures
- Histoire : l'univers de Ptolémée
- Histoire : l'héliocentrisme de Copernic
- Histoire : le géohéliocentrisme de Tycho-Brahe
- Histoire : les orbites elliptiques autour du soleil
- QCM
- Les trois lois de Kepler
- La première loi de Kepler
- La deuxième loi de Kepler
- La troisième loi de Kepler
- Exercice
- Exercice
- En savoir plus: les paramètres de l'ellipse
- Les distances dans le système solaire
- Parallaxe diurne, parallaxe horizontale
- La troisième loi de Képler
- La distance Terre-Mars
- La distance Terre-Vénus
- QCM
- La mécanique céleste
- Introduction
- Dynamique et gravitation
- Le principe fondamental de la dynamique
- En savoir plus: le principe fondamental de la mécanique
- Histoire : les débuts de la mécanique
- La gravitation universelle
- La mécanique céleste
- Dynamique du système solaire
- Le problème à deux corps
- Les mouvements dans le système solaire
- La vitesse de libération
- Les points de Lagrange
- Les satellites géostationnaires
- En savoir plus: calcul des périodes des satellites artificiels de la Terre
- Les transferts d'orbites par impulsion gravitationnelle
- Les satellites gardiens des anneaux
- QCM
- Les théories du mouvement des planètes
- Remarques générales sur les théories planétaires
- En savoir plus: théories analytiques ou intégration numérique ?
- En savoir plus: La découverte de Neptune par Le Verrier
- L'argument temps dans les théories planétaires
- Application : l'évolution de l'excentricité de l'orbite terrestre
- QCM
- La gravitation universelle et la relativité
- Introduction
- La gravitation newtonnienne
- Les limites de la gravitation universelle
- En savoir plus: l'excès d'avance du périhélie de Mercure
- La constante de la gravitation
- Exercice
- Les principes de la relativité
- La relativité galiléenne
- Les limites de la relativité galiléenne
- La relativité d'Einstein
- La relativité restreinte
- En savoir plus: la dynamique relativiste
- La relativité générale
- Les preuves expérimentales de la relativité générale
- QCM
- La mesure du temps
- Introduction
- Le temps astronomique
- Les mouvements de la Terre
- Définition du jour
- Temps vrai, temps moyen
- Les échelles de temps
- La précession et la nutation
- Les implications de la précession
- Définition de l'année
- L'heure
- Qu'est-ce-que l'heure ?
- Histoire de l'heure
- Une heure pour tous
- L'heure légale en France
- Le temps universel
- En savoir plus: les échelles de temps
- Les fuseaux horaires
- La ligne de changement de dates
- L'échelle de temps en physique
- Une seconde "fabriquée"
- Un étalon primaire de fréquence
- En savoir plus: les fontaines atomiques
- Calcul du Temps atomique international TAI
- Comparaison d'horloges à distance
- En savoir plus: la métrologie du temps
- Les calendriers
- Introduction
- Chronologie et ères
- Désignation des années
- Début des siècles et des millénaires
- Comment définit-on les calendriers ?
- Eres
- En savoir plus: la période julienne
- Calendriers
- Le calendrier julien
- Le calendrier grégorien
- En savoir plus: le calendrier copte
- En savoir plus: le calendrier musulman
- En savoir plus: le calendrier israélite
- En savoir plus: le calendrier républicain (1)
- En savoir plus: le calendrier républicain (2)
- En savoir plus: le calendrier indien
- En savoir plus: le calendrier perpétuel
- Les éphémérides
- Introduction
- Qu'est-ce qu'une éphéméride ?
- Modèles théoriques des mouvements
- Histoire des éphémérides
- Les différents types d'éphémérides
- Les éphémérides de position
- Ephémérides pour les observations physiques
- Le repérage des éphémérides de position
- Les systèmes de référence
- Les repères de référence célestes
- Les repères cinématiques liés aux étoiles
- Les repères dynamiques liés aux corps du système solaire
- Les systèmes de coordonnées
- Représentation des éphémérides
- Les éphémérides sous forme de tables
- En savoir plus: l'interpolation des éphémérides
- Les éphémérides sous forme graphique
- Détermination de la configuration des satellites de Jupiter à une date donnée
- Approximation d'une fonction par un polynôme
- En savoir plus: approximation de Tchebychev (1)
- En savoir plus: approximation de Tchébychev (2)
- En savoir plus: approximation de Tchébychev (3) exemple de calcul
- En savoir plus: approximation par des fonctions mixtes (1)
- En savoir plus: approximation par des fonctions mixtes (2)
- En savoir plus: Exemple de calcul
- La précision des éphémérides
- Les phénomènes astronomiques
- Qu'est-ce qu'un phénomène astronomique ?
- Lever et coucher d'un astre en un lieu donné
- Calcul d'un coucher ou d'un lever d'un astre
- Les phénomènes des satellites de Jupiter
- Où se procurer des éphémérides
- Où trouver des éphémérides imprimées ?
- Où trouver des éphémérides sur Internet ?
- Comment faire ses propres éphémérides ?
Introduction
Introduction à la notion de repère
Auteurs: P. Rocher, Jean-Eudes Arlot
Introduction
 Introduction
Introduction
Comment se repérer dans le ciel ?
Lorsque l'on regarde le ciel depuis le sol terrestre, nous voyons une voûte céleste constellée de points brillants (les étoiles) dont quelques uns en mouvement par rapport aux autres (les planètes), mais nous n'avons pas la sensation de nous mouvoir nous-mêmes dans l'espace. L'idée d'une Terre fixe au centre de l'univers s'impose tout naturellement, mais, à la réflexion, les choses ne sont
pas si simples que cela.

Crédit :
ASM/Gilles Bessou
Tout d'abord nous devons constater que les étoiles et les planètes ne restent pas fixes sur la voûte céleste. Leurs mouvements proviennent, d'une part du mouvement de la Terre autour de son axe (mouvement diurne), d'autre part du mouvement de la Terre autour du Soleil (mouvement apparent annuel du Soleil et des planètes), et enfin du mouvement propre de ces astres (insignifiant pour les étoiles mais régulier et très détectable pour les planètes). L'astronomie de position (ou astrométrie) et la mécanique céleste vont nous aider à déméler tous ces mouvements qui se superposent.
La voûte céleste
La sphère locale
Tout d'abord, notre perception du ciel est celle d'une sphère : étoiles et planètes sont toutes -apparemment- à la même distance de nous. Notre perception du relief, grâce à nos deux yeux, s'arrête en effet, à quelques dizaines de mètres de nous : au-delà, nous ne percevons plus de relief, donc plus de distances mais seulement des angles.
Nous sommes donc, chacun d'entre nous, le centre d'une sphère sur laquelle nous voyons les corps célestes : on l'appelle la sphère céleste locale et on va mesurer des angles sur cette sphère, puis à partir de ces angles et d'un modèle d'univers, on va en déduire la distance de ces points brillants que nous observons.
Dans la sphère céleste locale, on donne la position d'un astre avec deux valeurs, l'angle entre l'astre et l'horizon (mesuré verticalement) et l'angle entre la direction de l'astre et une direction fixe, par exemple le Sud (mesuré horizontalement).
Plus précisément, dans ce repère local, formé du plan de l'horizon et de la direction du Sud, on donne la position de l'astre avec les deux coordonnées :
L'angle azimutal ou azimut : est mesuré dans le plan de l'horizon, de 0 à 360 degrés à partir du Sud, positivement vers l'Ouest. La direction du Sud a donc un azimut de 0°, le point cardinal Ouest a un azimut de +90°, le point cardinal Nord est à +180° et par exemple le Nord-Ouest est à 135° d'azimut. Attention, les géomètres comptent l'azimut à partir du Nord, pas les astronomes !
L'altitude angulaire : c'est la hauteur dans le ciel mesurée de 0° à partir de l'horizon jusqu'à +90° au zénith (le point à la verticale de l'observateur).
Ce repère local dépend de l'observateur et varie d'un point à l'autre sur Terre.
Mais comment s'y retrouver entre observateurs du ciel qui sont à des endroirs différents sur Terre? D'autant plus qu'au-dessus d'un lieu donné, on ne voit pas toujours les mêmes étoiles...
Il faut construire un repère commun à tous les observateurs avec un plan origine, l'équateur (on comprendra plus tard pourquoi ce nom) et un méridien d'origine. Pour cela il y a plusieurs façons d'aborder le problème.
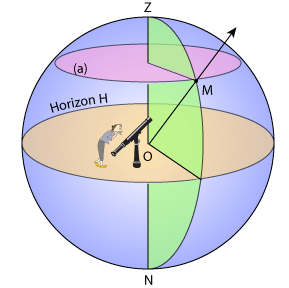
La sphère céleste locale définie par le plan horizontal (H, l'horizon du lieu) et le zénith (Z), l'observateur est en O.
Crédit :
ASM/Jean-Eudes Arlot et Damien Guillaume
Exercice
 La sphère céleste
La sphère céleste
Question 1)
Chaque observateur terrestre est entouré de sa sphère céleste locale dont il est le centre. Sa sphère locale est définie par le zénith du lieu, le plan horizontal et la direction Nord-Sud. Comment les observateurs de différents lieux terrestres pourront-ils comparer leurs mesures de position des astres ?
Il faut chercher des directions fixes communes à tous les observateurs. Quelles sont-elles ?
Le mouvement diurne
Pour déterminer un équateur dans le ciel, on remarque tout d'abord que toutes les étoiles semblent tourner sur des petits cercles autour de l'étoile polaire (c'est le mouvement diurne de la Terre). Ainsi, l'équateur terrestre se projette sur la sphère céleste et dessine un équateur céleste aisé à trouver. Ce mouvement amène à définir le repère céleste équatorial. Dans ce repère, tous les corps célestes, sauf la Lune, ont des coordonnées qui ne changent presque pas au cours de la nuit et très peu d'un jour à l'autre.
Le mouvement de rotation de la Terre autour de son axe apparaît donc de cette façon. Il faut donner ici quelques compléments sur le mouvement diurne. C'est le résultat de la rotation de la Terre autour de son axe. Cette rotation, repérée par rapport à une direction fixe (une étoile, par exemple), va durer 23h 56m 4s pour un tour complet (360°). Si on se repère par rapport à la direction du Soleil, il faudra alors 24h pour ramener celui-ci dans la même direction. En effet, durant sa rotation, la Terre s'est déplacée dans son mouvement de révolution autour du Soleil.
Le mouvement annuel
Au cours de l'année, les étoiles restent fixes les unes par rapport aux autres, mais les corps du système solaire, Lune, Soleil, planètes, bougent par rapport aux étoiles dans une bande du ciel autour de l'écliptique. Le plan de l'écliptique sert à définir le repère céleste écliptique.
Les repères, outils mathématiques pour se positionner
Auteur: P. Rocher
La notion de repère cartésien
Nous vivons et nous observons dans un espace à trois dimensions. Toute étude de mouvement dans notre environnement demande de positionner les corps par rapport à un repère de dimension trois. Le but du présent chapitre est de rappeler les notions de repère dans l'espace et les méthodes mathématiques qui permettent de changer de type de repère. On n'abordera pas dans ce chapitre la notion d'espace relativiste qui introduit le temps local comme quatrième dimension.
Vecteur unitaire sur un axe
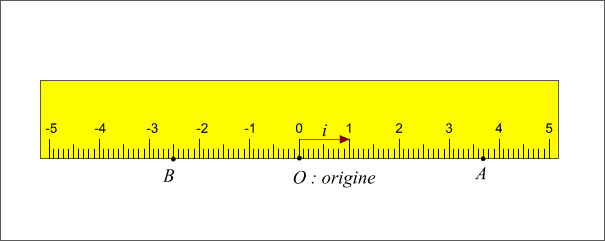
Figure 1: Vecteur unitaire sur un axe.
Crédit :
ASM/Patrick Rocher
On remarquera que nous n'avons pas indiqué d'unité de mesure sur le dessin, l'unité de mesure est la longueur du vecteur 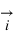 , ce vecteur porte donc le nom de vecteur unitaire.
, ce vecteur porte donc le nom de vecteur unitaire.
On peut également écrire que 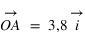 et que
et que 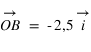 .
.
On remarquera également que chaque point de l'axe a une coordonnée et qu'inversement à chaque coordonnée correspond un point de l'axe. Cette propriété mathématique, appelée bijection entre le droite et l’ensemble des nombres réels, est fondamentale, car c’est elle qui permet de faire de la géométrie analytique.
Nota Bene : En mathématiques, le mot espace n'a pas le sens courant. Le 'plan' courant est un espace à 2 dimensions en mathématique et l''espace' courant est un espace à 3 dimensions en mathématiques. Il n'y a pas de mot courant pour les espaces à 4 (et plus) dimensions.
Se positionner dans le plan
Pour pouvoir se positionner dans le plan, on doit définir un repère ayant la même dimension que le plan : la dimension deux. Pour cela on utilise deux vecteurs unitaires notés 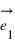 et
et 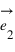 ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
Pour connaître la position d'un point A dans le plan par rapport au repère défini par les deux vecteurs, on va projeter le point A sur l'axe portant le vecteur 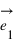 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 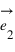 ; et sur l'axe portant le vecteur
; et sur l'axe portant le vecteur 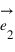 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 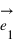 . Les coordonnées
. Les coordonnées 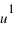 et
et 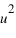 du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire : 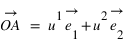 , les coordonnées
, les coordonnées 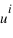 sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
Repère quelconque
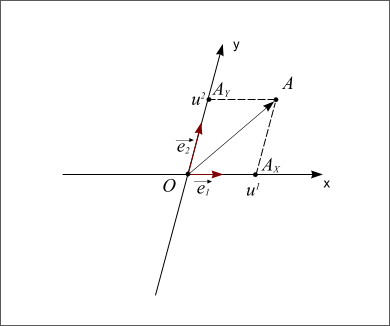
Figure 2: Repère direct quelconque
Crédit :
ASM/Patrick Rocher
Si les deux vecteurs sont perpendiculaires, le repère est dit orthogonal. Si les deux vecteurs ont la même longueur, on dit que le repère est normé. Et si les deux vecteurs sont perpendiculaires et s'ils ont la même longueur alors le repère est dit orthonormé. L'axe Ox porte le nom d'axe des abscisses et l'axe Oy porte le nom d'axe des ordonnées. Enfin si l'on passe de l'axe Ox à l'axe Oy par une rotation dans le sens inverse des aiguilles d'une montre (sens trigonométrique ou sens direct) on dit que le repère est direct. Dans le cas inverse, le repère est dit indirect.
Repère normé
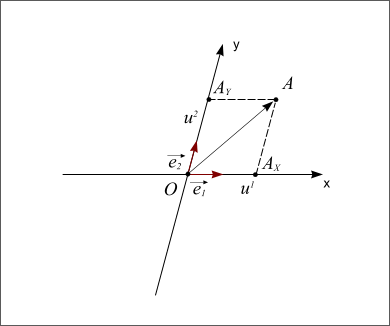
Figure 3 : Repère normé
Crédit :
ASM/Patrick Rocher
Repère orthonormé
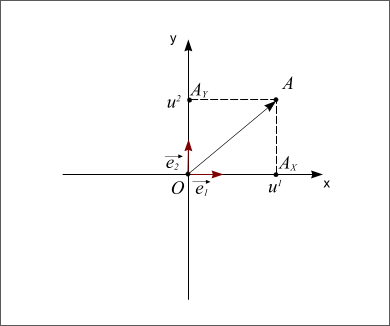
Figure 4 : Repère orthonormé
Crédit :
ASM/Patrick Rocher
Translation de repère
Changement d’origine d’un repère
L'usage de repère cartésien est très répandu, on l'utilise systématiquement lorsque l'on trace un graphique. Il est souvent intéressant de pouvoir déplacer le repère sans pour autant changer l'orientation de ses deux axes. On dit alors que le repère est en translation. Pour un point quelconque du plan, on distingue deux possibilités :
- Le point A est lié au repère, dans ce cas la position du point A dans le repère translaté est la même.
- Le point A n'est pas lié au repère, dans ce cas le point A ne se déplace pas avec le repère et ses coordonnées dans le repère translaté ne sont plus les mêmes.
Figure 5 : Point A lié au repère translaté
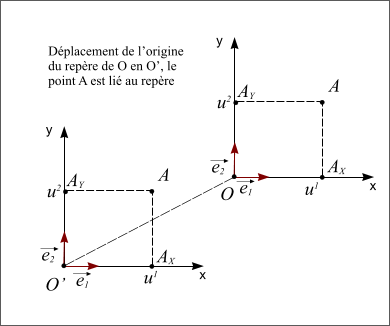
Figure 5 : Point A lié au repère translaté.
Crédit :
ASM/Patrick Rocher
Figure 6 : Point A non lié au repère tranlaté.
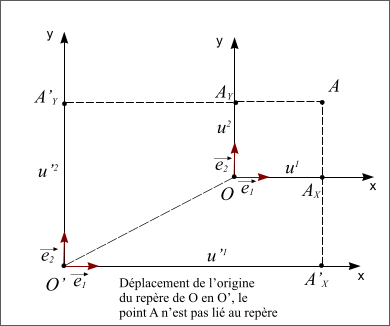
Figure 6 : Point A non lié au repère translaté.
Crédit :
ASM/Patrick Rocher
Rotation de repère
On peut également faire tourner le repère autour de son origine O, dans ce cas on peut également distinguer les points liés au repère qui vont tourner avec lui (dans ce cas leurs coordonnées ne changeront pas) et les points non liés au repère qui ne tourneront pas avec lui (dans ce cas leurs coordonnées vont changer).
Exercice : Calcul de coordonnées polaires dans le plan
Auteur: P. Rocher
 Calcul de coordonnées polaires
Calcul de coordonnées polaires
Soit un point A dans un repère orthonormé dont les coordonnées cartésiennes sont 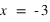 et
et 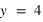 .
.
Question 1)
Calculer les coordonnées polaires de ce point , l'angle sera donné en degrés ?
Utiliser les formules du cours, attention aux unités pour l'angle si vous utilisez votre calculette.
Se positionner dans l'espace
Coordonnées cartésiennes
Pour se positionner dans l’espace, il convient d’ajouter une troisième dimension. Tout ce que nous avons dit pour les repères à deux dimensions se transpose pour les repères à trois dimensions.
La figure suivante représente un repère orthonormé direct, le troisième axe est l’axe Oz.
Repère orthonormé direct
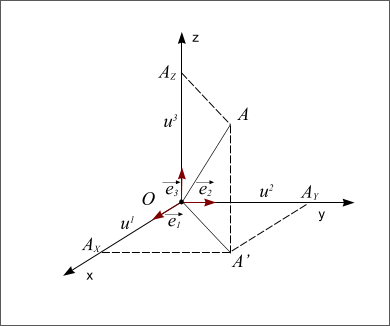
Figure 7 : Repère orthonormé direct.
Crédit :
ASM/Patrick Rocherr
Le point A est projeté orthogonalement en A’ sur le plan Oxy, puis A’ est projeté en AX sur l’axe Ox et en AY sur l’axe Oy. Le point A est également projeté orthogonalement en AZ sur l’axe Oz. Les coordonnées 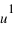 ,
,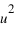 et
et 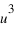 du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire : 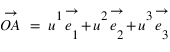 , les coordonnées
, les coordonnées 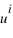 sont appelées coordonnées contravariantes du vecteur
sont appelées coordonnées contravariantes du vecteur 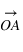 (ou projections parallèles). Elles sont souvent notées (x,y,z).
(ou projections parallèles). Elles sont souvent notées (x,y,z).
Exercice : Calcul des coordonnées polaires dans l'espace
Auteur: P. Rocher
 Calcul de coordonnées polaires
Calcul de coordonnées polaires
Difficulté : ☆☆☆
Question 1)
Le 18 janvier les coordonnées cartésiennes géocentriques de la Lune sont les suivantes : 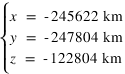 Calculer les coordonnées polaires (θ,φ,r) correspondantes, on donnera les valeurs des angles en degré, minute et seconde d'angle.
Calculer les coordonnées polaires (θ,φ,r) correspondantes, on donnera les valeurs des angles en degré, minute et seconde d'angle.
On fera attention aux signes de x et de y pour déterminer le bon angle φ.
Les unités angulaires
Le poids des traditions est très fort dans nos cultures, la standardisation des unités de mesure n’est pas toujours suivie d’effet et l’on trouve encore en fonction des pays et des publications des usages non standards. Ainsi les Anglo-saxons utilisent le mille terrestre international plus souvent que le mètre et les cartographes français utilisent encore le grade pour mesure les longitudes et les latitudes terrestres !
Les angles plans sont mesurés avec quatre systèmes d’unités :
Le radian
Le radian. La mesure d’un angle en utilisant cette unité se fait en radian et en fraction décimale de radian. C’est l’unité que l’on doit utiliser dans les calculs, en effet lorsque l'on dérive ou intègre une fonction trigonométrique l’angle doit être exprimé en radian.
Le degré sexagésimal
Le degré sexagésimal Cette unité est très ancienne, elle est basée sur le système sexagésimal qui permettait de faire des divisions facilement à l’époque où l’on connaissait mal les fractions. Le degré se divise en 60 minutes (symbole : ′), la minute se divise en 60 secondes (symbole : ″) etc. Dans le passé on divisait la seconde en 60 tierces (symbole : ′″) qui était elle-même divisée en 60 quatrièmes (symbole : IV). De nos jours on utilise plus les divisions inférieures à la seconde (on utilise les fractions décimales de la seconde), mais vous trouverez les anciennes notations dans les livres anciens. On remarquera que les symboles (′ - ″ - ′″ - IV ) correspondent à la numérotation romaine (I, II, III, IV) mise en exposant.
L'heure sexagésimale
L’heure sexagésimale L’heure se divise en 60 minutes (symbole : min), la minute se divise en 60 secondes (symbole : s). Il n’y a pas de divisions inférieures à la seconde (on utilise les fractions décimales de la seconde). Cette unité est encore largement utilisée en astronomie. Attention c’est une unité angulaire et non une unité de temps. L’unité de temps est définie à partir de la définition de la seconde de temps.
Le grade centésimal
Le grade centésimal Ce système est centésimal, ainsi le grade se divise en 100 minutes (symbole : ′) centésimales, la minute centésimale se divise en 100 secondes centésimales (symbole : ″) etc. On retrouve ici l’avantage du système centésimal, 23gr 35′ 25″ est égale à 23,3525 gr et si l’on prend le quadrant (angle droit) comme unité 0,233525 est directement le rapport de l’angle à l’angle droit.
On a les relations suivantes entre les différentes unités : 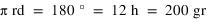
Exercice : conversion des unités
Auteur: P. Rocher
 Conversion des unités
Conversion des unités
Question 1)
Convertir un radian dans les différentes autres unités.
On donnera les valeurs trouvées en utilisant les subdivisions de chaque unités (par exemple h,min et secnde).
Les repères de l'astronomie "fixes"
Introduction
Nous allons décrire les repères astronomiques classiques. Ces dernières années, l’amélioration croissante de la précision des observations a nécessité des réformes importantes et la création de nouveaux repères célestes et terrestres que nous aborderons que très succinctement dans les pages « pour en savoir plus ».
Les repères quasi fixes
Historiquement, deux plans fondamentaux se sont imposés. Le premier est le plan de l’orbite apparente du Soleil vue depuis la Terre. Plus rigoureusement, il s'agit du plan de l'orbite du barycentre Terre-Lune. Ce plan est appelé écliptique, car c’est lorsque la Lune est proche de ce plan qu’il y a possibilité d’éclipse. Le Soleil, la Lune et les planètes sont toujours très proches de ce plan. Ce repère écliptique est utilisé pour étudier les mouvements des objets du système solaire.'
L’autre plan est le plan de l’équateur terrestre. Ce repère, le repère céleste équatorial est le repère principal pour les astrophysiciens (terriens!). Dans ce repère, les étoiles ont des coordonnées fixes.
Les astronomes ont construit un repère fondamental avec chacun de ces plans. Comme ces plans ne sont pas totalement fixes, ces repères sont définis pour un instant donné, par exemple pour l’instant correspondant au 1er janvier 2000 à 12h que l’on nomme époque J2000. De plus comme l’astronome observe et mesure uniquement des angles, on se limite souvent à des coordonnées polaires sur une sphère de rayon unité appelée sphère céleste.
Le repère céleste écliptique
Le repère écliptique J2000 est défini par le plan de base (Oxy) correspondant à l’orbite osculatricedu barycentre Terre-Lune autour du Soleil, la direction de l’axe Oz normale à ce plan (appelée pôle de l’écliptique) est choisie de sorte que le mouvement du barycentre Terre-Lune se fasse dans le sens direct (sens inverse des aiguilles d’une montre). Dans ce repère les coordonnées portent le nom de coordonnées écliptiques J2000. Les deux coordonnées polaires sont respectivement la longitude écliptique et la latitude écliptique. La longitude (notée 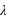 ) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée
) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée 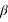 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
Repère écliptique
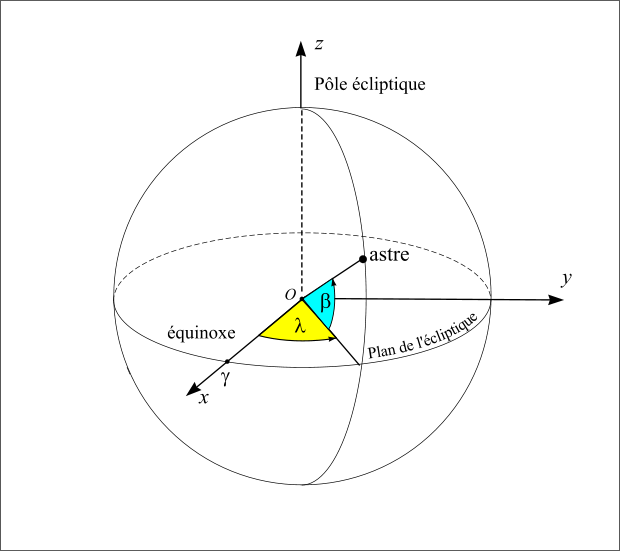
Figure 8 : Repère écliptique.
Crédit :
ASM/Patrick Rocher
Exercice
 Le repère écliptique
Le repère écliptique
Question 1)
Sachant que toutes les planètes se trouvent, comme le Soleil, dans l'écliptique ou très proches de l'écliptique, quelles sont, dans l’hémisphère nord, les meilleures conditions pour observer les planètes extérieures (Mars, Jupiter, Saturne, Uranus et Neptune) au plus haut dans le ciel nocturne ?
Dans l'hémisphère nord le Soleil culmine dans le ciel le jour du solstice d'été et il est au plus bas le jour du solstice d'hiver.
Ne pas oublier que le Soleil est toujours dans l'écliptique été comme hiver et que l'écliptique est toujours visible dans le ciel jour et nuit.
Le repère céleste équatorial
Le repère céleste équatorial
Le repère équatorial J2000 est défini par le plan de base (Oxy) correspondant au plan de l’équateur céleste (plan parallèle à l’équateur terrestre passant par le centre du repère) à l’instant considéré, la direction de l’axe Oz normale à ce plan (appelée pôle céleste nord) est choisie de sorte que le mouvement de la Terre autour de cet axe se fasse dans le sens direct (sens inverse des aiguilles d’une montre – donc d’ouest en est). Dans ce repère les coordonnées portent le nom de coordonnées équatoriales J2000. Les deux coordonnées polaires sont respectivement l’ascension droite et la déclinaison. L’ascension droite (notée 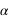 ) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée
) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée 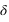 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée 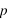 ).
).
Repère céleste équatorial
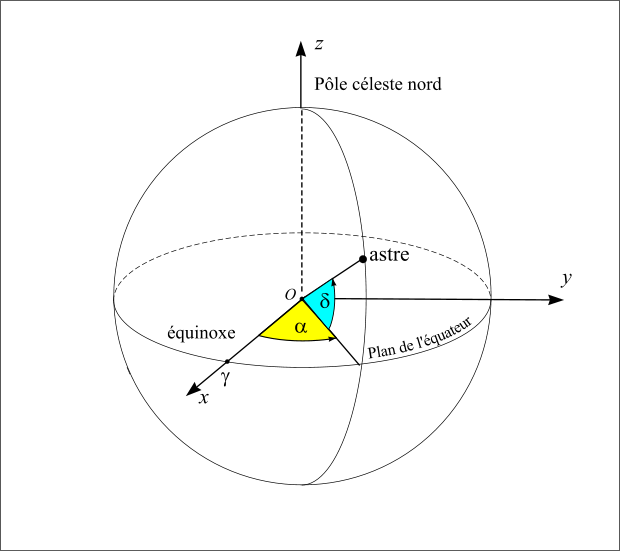
Figure 9 : Repère céleste équatorial.
Crédit :
ASM/Patrick Rocher
 Remarques
Remarques
On remarquera que nous n’avons pas encore précisé les directions origines Ox du repère écliptique et du repère équatorial. On pourrait définir des origines quelconques pour ces deux repères, mais comme l’axe de rotation de la Terre n’est pas perpendiculaire à son orbite, le plan de l’équateur n’est pas parallèle au plan de l’écliptique. L’intersection de ces deux plans est une droite que l’on nomme droite des équinoxes. Il était donc judicieux d’utiliser cette droite commune pour définir un axe Ox commun aux deux repères. Sur cette droite, on a le choix entre deux directions pour orienter l’axe Ox, on a choisi la direction de l’équinoxe correspondant au passage du Soleil des déclinaisons négatives aux déclinaisons positives dans son mouvement apparent annuel autour de la Terre. Cet équinoxe est appelé l’équinoxe de printemps ou point vernal. Il est noté pour la lettre gamma Υ, lettre grecque proche du symboledu signe du Bélier. La direction opposée est appelée direction de l’équinoxe d’automne, elle est notée par la lettre grecque oméga majuscule Ω proche du symbole du signe de la Balance.
Attention la direction de l’équinoxe de printemps est unique, elle ne change pas en fonction de l’hémisphère terrestre où l’on se trouve comme on le lit parfois. C’est le début de la saison astronomique qui change. Dans l’hémisphère nord le printemps commence lorsque le Soleil passe par l’équinoxe de printemps, cet instant correspond au début de l’automne dans l’hémisphère sud.
Changement de repère
Changement de repère
Les deux repères ayant le même axe Ox, on passe d’un repère à l’autre en faisant une rotation autour de cet axe Ox. Cet angle est l’angle que fait l’écliptique céleste avec l’équateur céleste. Il porte de nom d’obliquité de l’écliptique et est noté ε. Sa valeur à l’époque J2000 est proche de 23° 26' 21". Cet angle est également l’angle que fait l’axe de rotation de la Terre avec la normale à l’écliptique (pôle de l’écliptique).
Les deux repères (écliptique et équatorial).
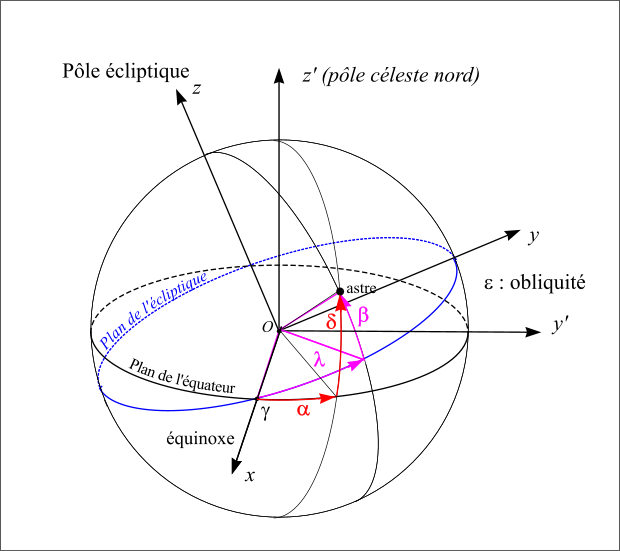
Figure 10 : Les deux repères (écliptique et équateur).
Crédit :
ASM/Patrick Rocher
Nouvelles définitions
Le grand cercle de la sphère céleste passant par les pôles célestes et les équinoxes porte le nom de colure des équinoxes. La droite perpendiculaire à la droite des équinoxes contenue dans le plan de l’écliptique porte le nom de droite des solstices. De même le grand cercle de la sphère céleste qui passe par les pôles célestes et les points solsticiaux porte le nom de colure des solstices. On remarquera que le colure des solstices passe également par les pôles de l’écliptique. Les colures des solstices et des équinoxes divisent l’équateur et l’écliptique en quatre secteurs égaux de 90°.
Selon l’origine des repères on parlera de :
- coordonnées barycentriques si l’origine est au barycentre du système solaire,
- coordonnées héliocentriques si l’origine est au centre de masse du Soleil,
- coordonnées géocentriques si l’origine est au centre de masse de la Terre,
- coordonnées topocentriques si l’origine est un lieu à la surface terrestre,
- coordonnées sélénocentriques si l’origine est au centre de masse de la Lune.
Formulaire de trigonométrie sphérique
Les formulaires de changement de repères en coordonnées polaires font appel à la trigonométrie sphérique.
Pour cela nous allons utiliser les formules de trigonométriques sphériques classiques.
Triangle sphérique
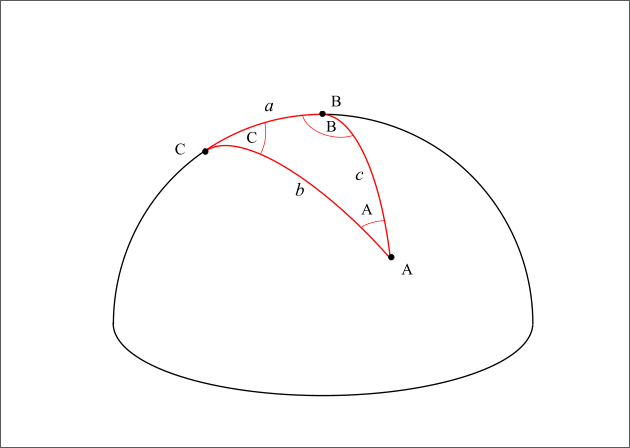
Figure 11 : Triangle sphérique.
Crédit :
ASM/Patrick Rocher
Considérons un triangle sphérique ABC formé par des arcs de grands cercles de la sphère, ce triangle possède trois angles aux sommets A, B et C et trois angles « côtés » a, b, c. A, B et C sont les angles entre les arcs de grands cercles et a, b et c sont les longueurs angulaires des arcs de grands cercles. Entre ces six angles, on a les relations trigonométriques suivantes :
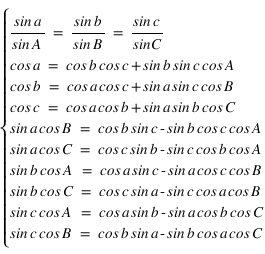
Il est inutile de connaître ces formules par cœur, il suffit de savoir qu’elles existent et de s’y rapporter lorsque l’on a un calcul à faire.
Relations entre les coordonnées polaires écliptiques et équatoriales
Si l’on trace les deux repères sur la sphère céleste et un astre quelconque en A, le pôle de l’écliptique PE, le pôle nord céleste P et la direction de l’astre A forme un triangle sphérique (PEPA).
Triangle sphérique, repères écliptique et équatorial.
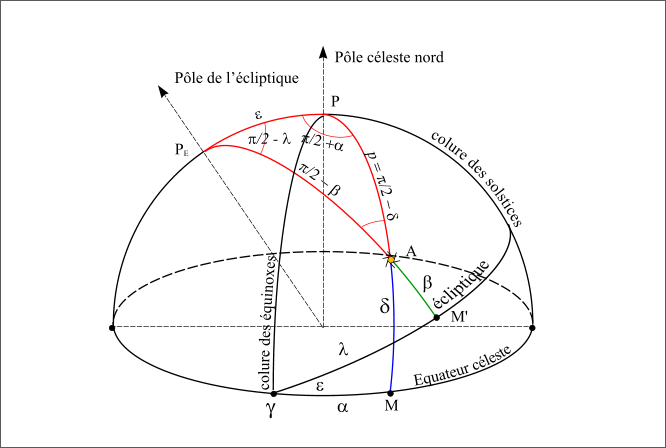
Figure 12 : Triangle sphérique, repères écliptique et équatorial.
Crédit :
ASM/Patrick Rocher
Dans ce triangle on connait cinq des six angles :
- L’arc PEP est l’obliquité ε,
- L’arc PEA est le complémentaire de la latitude écliptique :
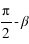 ,
, - L’arc PA est la distance polaire ou le complémentaire de la déclinaison :
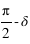 ,
, - L’angle entre l’arc PEP et l’arc PEA est le complémentaire de la longitude écliptique :
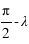 ,
, - L’angle entre PEP et PA est égal à 90° (π/2) l’angle entre les deux colures plus l’ascension droite de l’astre :
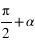 .
.
Pour avoir par exemple les coordonnées équatoriales en fonction des coordonnées écliptiques, il suffit d’écrire les relations suivantes :
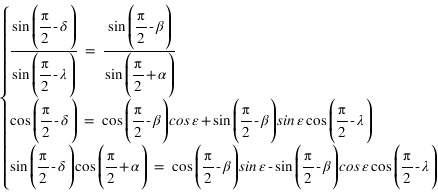
Ce qui donne après simplification :
Système (1) 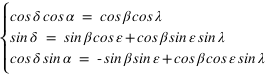
La déclinaison s’obtient à l’aide de la seconde relation en prenant l’arc sinus de sin δ (car δ est compris en –90° et +90°) l’ascension droite est obtenue grâce à la première et à la troisième relation. La connaissance du sinus et du cosinus de l’ascension droite permet de connaître l’ascension droite sur l’intervalle allant de 0° à 360°. On doit ensuite mettre ces deux variables dans le bon système d’unités (heures sexagésimales pour l’ascension droite et degrés sexagésimaux pour la déclinaison).
On a des relations identiques pour passer des coordonnées équatoriales aux coordonnées écliptiques.
Système (2) 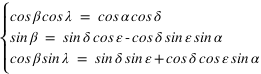
Auteur: ASM/Patrick Rocher
 Calcul des coordonnées équatoriales du Soleil
Calcul des coordonnées équatoriales du Soleil
Cet exercice a pour but de vous faire calculer les coordonnées équatoriales du Soleil à partir de ces coordonnées écliptiques.
Pour simplifier, le calcul on supposera que la latitude du Soleil β est nulle, ce qui implique que 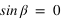 et que
et que 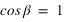 . Le système (1) est donc simplifié.
. Le système (1) est donc simplifié.
Question 1)
Le 1 janvier 2012 à 0h UTC, la longitude apparente λ du Soleil est de 279° 57' 30", calculer son ascension droite et sa déclinaison sachant que l'obliquité de l'écliptique ε à cet instant est de 23°26' 12,7". On exprimera l'ascension droite en heures, minutes et secondes d'angle et la déclinaison en dégres, minutes et secondes d'angle.
Le système (1) lorsque l'on prend une latitude nulle à la forme simplifier suivante : 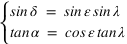 .
Faites attention aux unités, la calculatrice en ligne utilise des radians !
.
Faites attention aux unités, la calculatrice en ligne utilise des radians !
Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique 
Cette simulation a pour but de vous montrer le mouvement du Soleil apparent sur l'écliptique.
Elle montre l'inclinaison de l'écliptique sur l'équateur céleste (noté ε), la longitude écliptique du Soleil apparent et les coordonnées équatoriales (ascension droite α et déclinaison δ). P est le pôle Nord céleste et K est le pôle Nord de l'écliptique.
Dans cette simulation, la latitude du Soleil est supposée nulle, en réalité la latitude du Soleil est très faible et varie en fonction du temps. Cet écart provient du fait que l'écliptique est construit à partir du mouvement du barycentre Terre-Lune alors que les coordonnées du Soleil sont calculées depuis le centre de la Terre.
Remarques
Les coordonnées équatoriales du Soleil variant peu au court d'une journée, on peut utiliser cet applet pour calculer les coordonnées équatoriales du Soleil un jour donné.
On vérifiera deux choses importantes :
Auteur: P. Rocher
 Variation journalière de la longitude et de l'ascension droite du Soleil
Variation journalière de la longitude et de l'ascension droite du Soleil
Question 1)
Placez-vous le 5 janvier 2012, noter la longitude. Avancez d'un jour est refaite la même mesure. En déduire la variation journalière en longitude. Refaites la même mesure pour le 5 et le 6 juillet 2012. Que peut-on en déduire?
Question 2)
Le jour de l'équinoxe de printemps est le jour où la longitude du Soleil passe par 0°, celui de l'équinoxe d'automne est celui où la longitude du Soleil est égale à 180°. Les jours des solstices d'été et d'hiver correspondent respectivement au jour où la longitude du Soleil passe par 90° et 270°. Calculez les dates des saisons pour une année donnée.
Les mouvements du repère équatorial
En fait la direction de l’axe instantané de rotation de la Terre n’est pas constante. Historiquement le mouvement de cet axe a été décomposé en deux parties : une composante circulaire appelée précession et une composante formée de multiples variations périodiques appelée nutation. La composante circulaire fait parcourir à l’axe de rotation de la Terre un cône dans le sens rétrograde à la vitesse d’environ 50″ par an (un tour en environ 26000 ans). Cette précession se traduit par un mouvement de l’axe des équinoxes à la même vitesse également dans le sens rétrograde (appeler précession des équinoxes). On peut donc définir des repères écliptiques et équatoriaux dans lesquels on corrige de la précession, pour une date donnée, la position de l’équinoxe. Dans ce cas les repères sont dits moyens de la date.
On peut aussi définir des repères écliptiques et équatoriaux dans lesquels on corrige, pour une date donnée, la position de l’équinoxe de la précession et de la nutation (qui agit également sur l’obliquité de l’écliptique). Dans ce cas les repères sont dits vrais de la date.
On voit l’importance de la connaissance du mouvement de l’axe de rotation de la Terre.
On voit également que le repère écliptique dépend de la théorie du barycentre Terre-Lune et que l’usage d’une origine tournante, la direction de l’équinoxe n’est forcément judicieuse, car elle varie en fonction de la théorie de la précession utilisée.
Précession des équinoxes
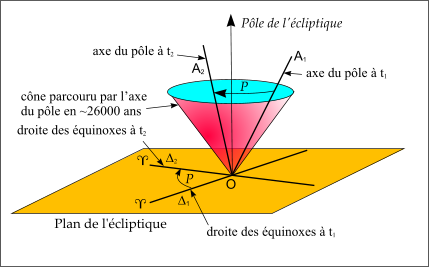
Figure 13 : Précession des équinoxes.
Crédit :
ASM/Patrick Rocher
La médiation
La médiation est une notation hybride basée sur les deux repères écliptique et équatorial. Considérons le cercle horaire portant l’astre A. Ce cercle horaire coupe l’équateur céleste en H et il coupe l’écliptique en MA que l’on nomme point de médiation de l’astre A. On appelle médiation de l’astre A l’arc 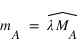 , sa longitude écliptique étant λ , M étant la projection de la direction de l’astre sur l’écliptique.
, sa longitude écliptique étant λ , M étant la projection de la direction de l’astre sur l’écliptique.
Parfois on donne le couple de coordonnées formé par la médiation et la déclinaison à la place des coordonnées équatoriales classiques (ascension droite et déclinaison). Ce couple de coordonnées n’est pas orthogonal, mais il est parfois utilisé notamment dans les instruments anciens (astrolabe).
La médiation d'un astre.
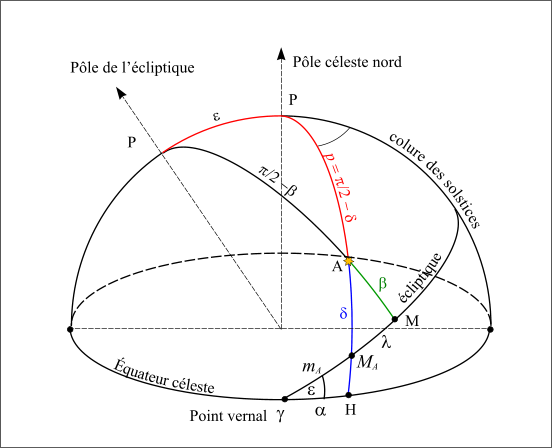
Figure 14 : La médiation d'un astre.
Crédit :
ASM/Patrick Rocher
Le repère galactique J2000
Les astronomes utilisent également un repère particulier pour positionner les étoiles par rapport au plan de notre galaxie : le repère galactique.
Le repère galactique
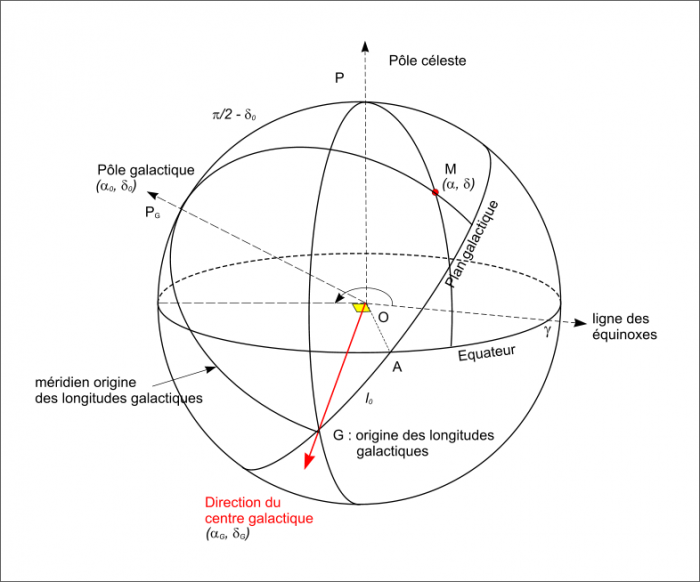
Figure 15 : Le repère galactique.
Crédit :
ASM/Patrick Rocher
Soit PG (α0, δ0) la direction du pôle galactique dans le repère équatorial J2000 et OG (αG, δG) la direction du centre galactique dans ce même repère. Les coordonnées géocentriques galactiques J2000, la longitude et latitude galactiques sont définies dans le repère direct construit à l’aide du plan galactique et le pôle galactique. Le méridien origine des longitudes étant défini par la direction du centre galactique. Nous noterons l0 l’angle AG (positif dans le sens rétrograde). L’ascension droite αA du point A est égale α0 + π/2 et l’inclinaison i du plan galactique sur l’équateur est égale à α0 – π/2. Le plan galactique ainsi défini est le plan passant par le centre de la Terre, normal à la direction du pôle galactique. Ce repère est un repère géocentrique J2000, car il est défini par rapport au repère fixe équatorial J2000.
Les coordonnées terrestres
Les coordonnées terrestres sont données par rapport au pôle terrestre et le plan de l’équateur terrestre. Ce système constitue un référentiel terrestre. Les coordonnées polaires terrestres portent les noms de latitude (notée φ) et longitude (notée L) terrestres. L’axe instantané de rotation de la Terre se déplace par rapport aux étoiles, mais il reste quasi fixe par rapport à la croûte terrestre.
Par contre la Terre n’étant pas parfaitement sphérique (elle est aplatie aux pôles), on doit distinguer deux types de coordonnées : des coordonnées géographiques (ou astronomiques) et des coordonnées géocentriques.
En première approximation la Terre est assimilée à un ellipsoïde de révolution.
Un méridien terrestre est un arc de longitude constante joignant les deux pôles terrestres.
Sur cet ellipsoïde on définit un méridien origine passant par les deux pôles géographiques. Ce méridien origine porte le nom de méridien international (méridien de Greenwich). Pour un lieu donné, on distingue une seule longitude et deux latitudes :
- la latitude géocentrique φ' qui est l’angle entre la direction allant du centre de la Terre au lieu considéré et le plan de l’équateur terrestre,
- la latitude géographique ou astronomique φ qui est l’angle entre la normale à l’ellipsoïde de référence et le plan de l’équateur terrestre.
coordonnées géographiques
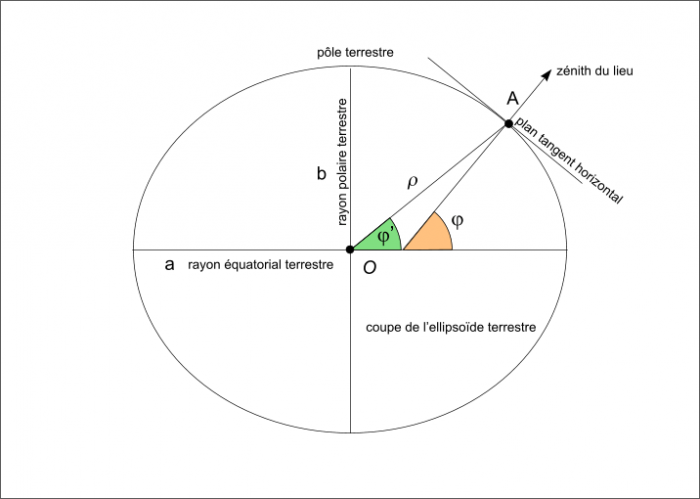
Figure 16 : Coordonnées géographiques.
Crédit :
ASM/Patrick Rocher
Historiquement les latitudes géographiques étaient obtenues à l’aide de mesures de hauteur d’astre aux dessus de l’horizon.
La longitude est comptée à partir du méridien international en heures ou en degrés sexagésimaux. Historiquement les longitudes géographiques étaient obtenues à l’aide de mesures astronomiques (point astronomique).
De nos jours les coordonnées géographiques sont obtenues à l’aide de systèmes satellitaires (GPS).
Sur une planète on parlera de coordonnées planétographiques et de coordonnées planétocentriques.
Calcul des coordonnées géocentriques
Soit φ la latitude géographique, φ' la latitude géocentrique et h l’altitude du lieu.
a est le rayon équatorial terrestre et f est l’aplatissement de l’ellipsoïde terrestre.
ρ est la distance entre le centre de la Terre et le lieu exprimé en rayon terrestre équatorial.
On a les relations suivantes :
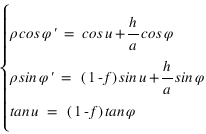
La connaissance des quantités 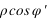 et
et 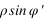 est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
Quelques ellipsoïdes de références
| Système géodésique | Ellipsoïde associé | aen mètres | b en mètres | f |
|---|
| NTF | Clarke 1880 IGN | 6378249,2 | 6356515,0 | 1/293,466021 |
| ED50 | ED50 Hayford 1909 | 6378388,0 | 6356911,9461 | 1/297,000000 |
| WGS84 et RGF 83 | IAG GRS 1980 | 6378137,0 | 6356752,314 | 1/298,257222 |
Auteur: P. Rocher
 Calcul de la latitude géocentrique de Paris
Calcul de la latitude géocentrique de Paris
Les coordonnées géographiques de l'Observatoire de Paris sont les suivantes :Latitude géographique : 48° 50' 11,2" N, longitude géographique : 2° 20' 13,8" E, altitude : 67m.
Question 1)
Calculer les coordonnées géocentriques de l’Observatoire de Paris en utilisant le système géodésique WGS84.
On calculera d'abord la valeur de u, puis les valeurs de 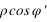 et
et 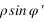 .
.
Les repères locaux
Auteur: Patrick Rocher
Introduction
Les deux repères écliptique et équatorial sont fixes pour une époque donnée, même centrés au centre de la Terre, ils ne tiennent pas compte du mouvement de l’observateur, ni de sa position. Nous allons décrire deux nouveaux repères qui vont être liés à un observateur sur la Terre. Ces repère vont donc tourner avec notre planète. Nous devons donc, dans un premier temps, exprimer la rotation de la Terre par rapport au répère équatorial terrestre.
Le système de coordonnées équatoriales horaires
Le temps sidéral
Ce système est un système intermédiaire dans lequel le repère équatorial est lié à la Terre, c’est-à-dire qu’il tourne avec elle. Il est caractérisé par un méridien origine (le méridien du lieu) et un angle qui donne la position du point vernal (direction de l’équinoxe de printemps) par rapport à ce méridien. Cet angle s’appelle le temps sidéral local (noté TL). Cet angle est exprimé en heures sexagésimales, il est compté positivement vers l’ouest (sens des aiguilles d’une montre) à partir du méridien local. Ainsi l’angle temps sidéral local croît avec le temps.
Le temps sidéral local à Greenwich
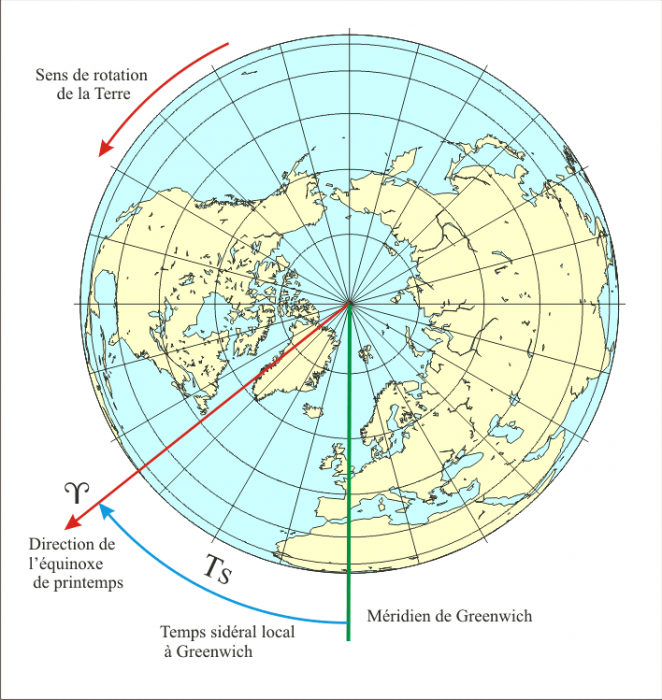
Figure 17 : Le temps sidéral local.
Crédit :
ASM/Patrick Rocher
Les coordonnées équatoriales horaires
Le système de coordonnées équatoriales horaires est un système polaire dont le plan de base (Oxy) est l’équateur céleste, Ox est la direction du méridien local, Oy est dans le sens indirect (90° vers l’ouest) et Oz est l’axe du pôle céleste. Le premier angle est l’angle horaire (noté H), compté positivement en heures sexagésimales de 0h à 24h vers l’ouest à partir du méridien du lieu, le second angle est la déclinaison (le même angle que celui du repère équatorial). L’angle horaire, comme le temps sidéral, croît avec le temps.
Les petits cercles parallèles à l’équateur portent le nom de parallèles célestes et les demi-grands cercles joignant les pôles célestes portent le nom de cercles horaires. Tous les astres qui ont une déclinaison constante décrivent dans le mouvement diurne un parallèle céleste. En particulier, l'étoile Polaire décrit actuellement un petit cercle dont le rayon est inférieur à 1° autour du pôle céleste, ce qui nous permet de situer le pôle céleste à un degré près. Cela n’a pas toujours été le cas. Ainsi au XIIIe siècle d’étoile polaire était à 4° du pôle céleste cela en raison de la précession des équinoxes.
Repère équatorial horaire
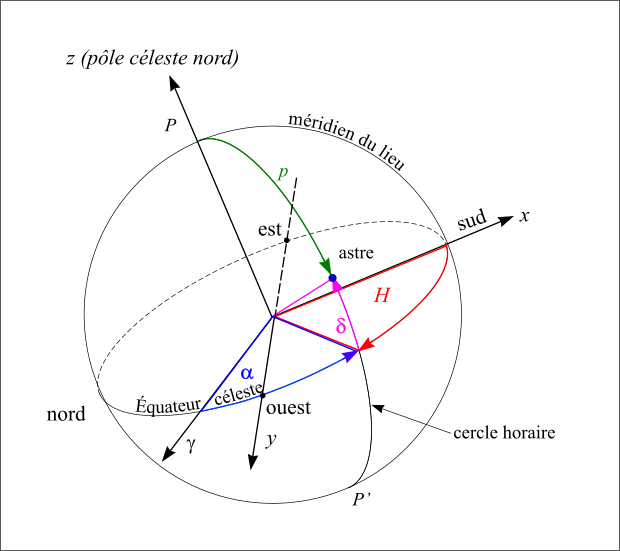
Figure 18 : Repère équatorial local.
Crédit :
ASM/Patrick Rocher
On a une relation simple entre l’ascension droite, l’angle horaire et le temps sidéral local :
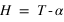
Attention dans les formules ces angles doivent être dans le même système d’unités.
On remarquera que l’angle horaire d’un astre est le même pour tous les lieux situés sur un même méridien terrestre.
Compte tenu de la définition de l’angle horaire, le temps sidéral local est l’angle horaire du point vernal.
Exercice
 Le temps sidéral
Le temps sidéral
Question 1)
Quelle est l'ascension droite α d'une étoile passant au méridien d'un lieu donné à un instant donné ?
Quelle est la valeur de l'angle horaire d'un astre qui passe au méridien? Quelle est la formule fondamentale liant l'ascension droite et l'angle horaire?
Effet d'un changement de longitude terrestre
Si l’on change de méridien, à un instant donné, le temps sidéral local du nouveau méridien est égal au temps sidéral de l’ancien méridien augmenté de la différence de longitude si le nouveau méridien est à l’est de l’ancien ou diminué de la différence de longitude si le nouveau méridien est à l’ouest de l’ancien. Attention les longitudes doivent être dans le même système d’unités que le temps sidéral (généralement en heures sexagésimales). Attention également aux conventions pour la notation des longitudes : dans le passé les longitudes étaient comptées négativement vers l’est (de 0° à -180° ou 0h à -12h) et positivement vers l’ouest (de 0° à 180° ou 0h 12h) à partir du méridien de Greenwich. La formule donnant le temps sidéral local TL en un lieu de longitude L par rapport au temps sidéral à Greenwich TG était donc :
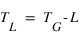
De nos jours les conventions sur la longitude ont changé, la longitude est comptée positivement vers l’est à partir du méridien de Greenwich de 0° à 360° (ou de 0h à 24h) la formule précédente se transforme donc en :
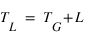
On trouve donc les deux formules dans la littérature et cela est la source de nombreuses erreurs de calcul. Pour les éviter, il suffit de se souvenir que le temps sidéral croît par rapport à Greenwich lorsque la longitude est vers l’est et décroit lorsque la longitude est vers l’ouest. N’oubliez pas non plus que certaines cartes donnent la longitude par rapport au méridien de Paris en grade !
La variation du temps sidéral
Le temps sidéral est l’angle horaire de la direction de l’équinoxe de printemps (le point gamma), il varie (en moyenne) de 24h (ou 360°) en 23h 56min 4s de temps moyen.
Cela permet de calculer le temps sidéral local en tout point de la Terre à un instant t à partir de la connaissance du temps sidéral au méridien de Greenwich à 0h. Le calcul se fait en deux étapes : on calcule le temps sidéral à Greenwich à l’instant t, puis le temps sidéral au lieu considéré en ajoutant ou en retranchant la longitude du lieu.
Relations entre la variation du temps moyen 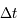 et la variation
et la variation 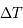 du temps sidéral :
du temps sidéral :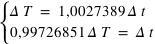
Nous sommes capables de construire une horloge de temps sidéral local. Sur ces horloges, l’aiguille des heures fait deux tours en 23h 56min 4s de notre échelle de temps. La connaissance du temps sidéral est importante, car elle permet de calculer l’angle horaire d’un astre (angle qu’il fait avec la direction du sud, lorsque l’on connaît son ascension droite. Inversement lorsque l’on connait le temps sidéral local d’un événement on peut en déduire :
- le temps moyen de l’événement si on connaît la longitude du lieu,
- la longitude du lieu si l’on connaît le temps moyen de l’événement.
Remarque : Comme ce repère local ne dépend que de la longitude, on peut le placer au centre de la Terre ou sur un lieu quelconque situé sur le méridien. Nous verrons que ce changement d’origine modifie la valeur des coordonnées pour des astres proches (parallaxe diurne).
Auteur: P. Rocher
 Calcul du temps sidéral local en un lieu donné
Calcul du temps sidéral local en un lieu donné
Difficulté : ☆☆☆
Question 1)
Déterminer le temps sidéral local à Paris le 30 mars 2010 à 18h 3m 42s UTC (l’heure UTC est le temps moyen de Greenwich) à Paris (longitude : 9min 21s est). Le temps sidéral à Greenwich à 0hUTC étant de 12h 29min 7s.
Faire une règle de trois en sachant qu'en 23h 56min 4s de temps moyen le temps sidéral varie de 24h ou utiliser directement les formules de conversions.
Le repère local
En un lieu donné, de latitude géographique φ et de longitude géographique L on peut définir un repère local dont le plan Oxy est par le plan horizontal tangent à l’ellipsoïde au lieu considéré et dont l’axe Oz est la normale à ce plan (direction du zénith). Comme dans le cas des coordonnées horaires, l’axe Ox est l’intersection du plan du méridien et du plan horizontal (direction du sud) et l’axe Oy est à 90° compté vers l’ouest dans le sens indirect (direction de l’ouest). On appelle premier vertical ouest le demi-plan vertical passant par la verticale du lieu et la direction de l’ouest. On définit de même le premier vertical est comme le demi-plan vertical passant par la direction de l’est.
Le premier angle est compté positivement à partir du sud vers l’ouest (sens indirect – sens des aiguilles d’une montre) de 0° à 360° et s’appelle l’azimut des astronomes (noté a). On a donc les relations suivantes :
sud ⇔ azimut = 0°, ouest ⇔ azimut = 90°, nord ⇔ azimut = 180° et est ⇔ azimut = 270°. La direction de la vertical, vers le haut, d'un lieu porte le nom de zénith, sa direction opposée, vers le bas, porte le nom de nadir.
Le second angle est compté positivement vers le zénith de 0° à 90°et négativement vers le nadir de 0° à –90°, il porte le nom de hauteur (noté h). À la place de la hauteur, on utilise parfois l’angle entre la direction du zénith et la direction de l’astre, cet angle est compté de 0° à 180° à partir du zénith et porte de nom de distance zénithale (notée z).
Repère local azimutal
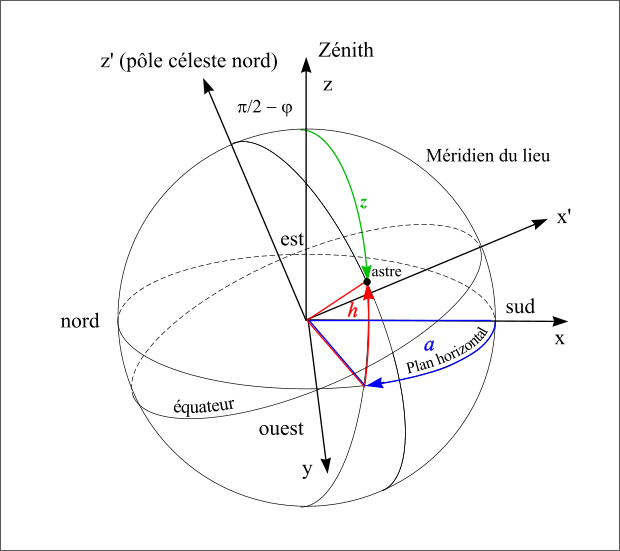
Figure 19 : Repère local azimutal.
Crédit :
ASM/Patrick Rocher
Quelques définitions supplémentaires
Lors du lever d’un astre, sa hauteur apparente est nulle (h = 0), on donne parfois l’angle entre la direction de l’est et la direction de l’astre à son lever, cet angle porte le nom d’amplitude ortive. De même lors du coucher d’un astre, on donne parfois l’angle entre la direction de l’ouest et la direction de l’astre à son coucher, cet angle porte le nom d’amplitude occase.
Enfin les cercles de hauteurs égales, petits cercles de la sphère céleste parallèles à l’horizon, portent le nom almicantarat.
Pour un lieu de l’hémisphère nord, l’angle entre le zénith et le pôle céleste nord est égal au complémentaire de la latitude du lieu (π/2 – φ). Le complémentaire de la latitude porte le nom de colatitude.
C’est aussi l’angle entre le plan équatorial céleste et le plan horizontal.
Formulaires liant les coordonnées locales
Le triangle sphérique construit avec le pôle céleste nord, le zénith du lieu et la direction d’un astre est le suivant :
triangle-local
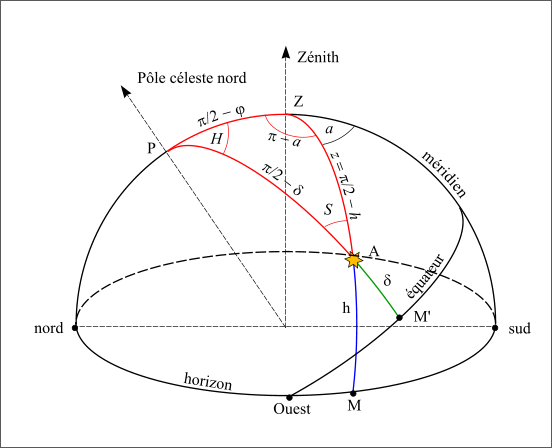
Figure 20 : Triangle sphèrique local.
Crédit :
ASM/Patrick Rocher
En utilisant les relations de trigonométrie sphérique sur les cinq angles connus, on démontre les relations suivantes :
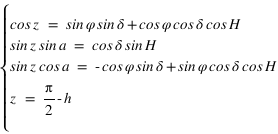
et inversement
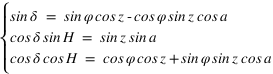
Le sixième angle, formé par les directions du zénith et du pôle céleste vues depuis l’astre porte le nom d’angle à l’astre (noté S).
Remarque sur le repère local (alt-azimutal)
Les géographes et les marins utilisent un azimut compté également dans le sens indirect, mais à partir du nord. L’azimut d’un astre pour un lieu de l’hémisphère nord croît avec le temps ainsi le Soleil se déplace d’est en ouest en passant vers le sud.
Inversement dans l’hémisphère sud l’azimut décroit avec le temps, ainsi le Soleil se déplace d’est en ouest en passant vers le nord.
Les montres ayant été inventées dans l’hémisphère nord, les aiguilles de la montre suivent le mouvement de l’ombre des cadrans solaires de l’hémisphère nord donc est-sud-ouest.
Dans l’hémisphère nord la hauteur du pôle céleste est égale à la latitude du lieu (en fait ce n’est pas tout à fait vrai en raison de la réfraction atmosphérique).
Simulations
Pour bien comprendre les systèmes de coordonnées, on peut utiliser les simulations suivantes.
 Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales 
La première simulation affiche la position d'un astre sur la sphère céleste, en coordonnées équatoriales (α, δ) et en coordonnées horizontales (a, h). On y voit aussi le point vernal γ et l'angle horaire H. Z est le zénith et P est le pôle céleste.
Les paramètres de la simulation sont les suivants :
- Coordonnées équatoriales de l'astre, ascension droite α et déclinaison δ ;
- position sur Terre, latitude φ et longitude L ;
- date et heure en temps universel.
En bas de la simulation, on trouve les données calculées à partir des paramètres : angle horaire H, hauteur h et azimut a.
On peut trouver les coordonnées et le fuseau horaire d'une ville sur le web.
 Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique 
La deuxième simulation montre la position du Soleil sur l'écliptique à une date donnée. Cette simulation montre l'inclinaison de l'écliptique par rapport à l'équateur ε, la longitude écliptique λ, l'ascension droite α et la déclinaison δ. P est le pôle Nord céleste et K est le pôle Nord de l'écliptique. Les quantités calculées par rapport à la date et affichées en bas sont λ, α et δ.
Les coordonnées équatoriales du Soleil variant peu au court d'une journée, on peut les obtenir à partir de cette simulation pour une date donnée, et les utiliser dans la première simulation pour voir la position du Soleil en coordonnées horizontales pendant la journée.
Exercices d'utilisation des simulations
Auteur: Damien Guillaume
 Visibilité des étoiles
Visibilité des étoiles
Difficulté : ☆☆
Cet exercice propose d'utiliser l'applet Coordonnées équatoriales et horizontales pour déterminer la visibilité d'étoiles en différents endroits sur Terre.
Données
- Sirius : ascension droite α = 6h 45m, déclinaison δ = -16° 43'
- Dubhe : α = 11h 04m, δ = +61° 45'
- France (Paris) : latitude φ = +49°, longitude L = 2° E, fuseau horaire = UTC+1
- Afrique du Sud (Cape Town) : φ = -34°, L = 18° E, UTC+2
- Japon (Tokyo) : φ = 36° N, L = 140° E, UTC+9
Question 1)
A l'aide de l'applet, trouver les mois de l'année où Sirius est visible à minuit en France (à Paris), en Afrique du Sud (Cape Town) et au Japon (Tokyo).
Attention au décalage horaire !
Pour simplifier, on pourra prendre minuit heure locale sans tenir compte des différences heures d'été / heures d'hiver.
Par convention, la longitude est positive vers l'Est. Donc 140° E = +140°.
Question 2)
Même question pour l'étoile Dubhe (α UMa).
Question 3)
Expliquer les résultats.
Applications liées au repère local
Auteur: P. Rocher
Introduction
Tout ce que nous observons depuis la Terre se fait dans le repère local. Habitant dans l'hémisphère nord, nous sommes habitués à voir un ciel et des phénomènes liés à notre hémisphère. Nous allons dans les rubriques suivantes décrire des phénomènes pour un lieu quelconque de la Terre.
Quelques définitions supplémentaires
Un demi-cercle de la sphère céleste joignant le zénith au nadir porte le nom de demi-cercle d’égal azimut.
Le demi-cercle de la sphère céleste joignant le pôle céleste nord au pôle céleste sud et contenant le zénith porte le nom de méridien supérieur, par définition tous les points de ce demi-cercle ont un angle horaire nul (H = 0h = 0°), ce demi-cercle est toujours l’origine des angles horaires.
Le demi-cercle de la sphère céleste joignant le pôle céleste nord au pôle céleste sud et contenant le nadir porte le nom de méridien inférieur, par définition tous les points de ce demi-cercle ont un angle horaire de 12h (H = 12h = 180°).
Le demi-cercle d’égal azimut contenant le pôle céleste sud est souvent appelé méridien sud, c’est un abus de langage on devrait parler de demi-cercle d’azimut nul (a = 0°) ou d’azimut sud, ce demi-cercle est toujours l’origine des azimuts.
Le demi-cercle d’égal azimut contenant le pôle céleste nord est souvent appelé méridien nord, c’est également un abus de langage on devrait parler de demi-cercle d’azimut 180° (a = 180°) ou d’azimut nord.
Les astres circumpolaires
Suite à la rotation de la Terre autour de son axe, tous les astres passent au méridien inférieur et au méridien supérieur.
- Si les deux passages sont observables, l’astre est dit circumpolaire, il ne se couche pas.
- Si les deux passages sont inobservables, l’astre ne se lève pas.
- Si seul le passage supérieur est observable, l’astre se lève et se couche.
Par observable on entend que le passage serait visible en absence de Soleil c’est-à-dire qu’il n’aurait pas lieu sous l’horizon.
Astres circumpolaires
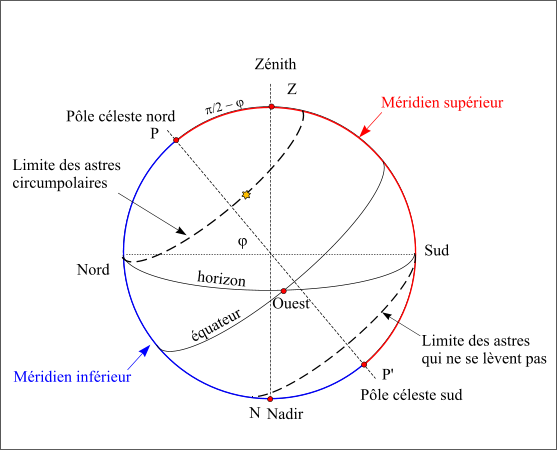
Figure 21 : Astres circumpolaires.
Crédit :
ASM/Patrick Rocher
Astres ayant une plus grande digression est et ouest
Par contre, tous les astres ne passent pas tous au méridien nord et au méridien sud, en effet certains astres passent deux fois dans le méridien nord (a = 180°) ou deux fois dans le méridien sud (a = 0°). Pour un lieu de l’hémisphère nord, ce sont les astres qui passent entre le zénith et le pôle céleste nord (observable) ou entre le nadir et le pôle céleste sud (inobservable, car toujours sous l’horizon). Comme l’azimut ne varie plus de 0° à 360°, il présente deux valeurs extrêmes (une entre 0° et 180° et l’autre entre 180° et 360°). C’est deux valeurs extrêmes correspondent aux plus grandes digressions ouest et est de l’astre.
Plus grande digression d'un astre.
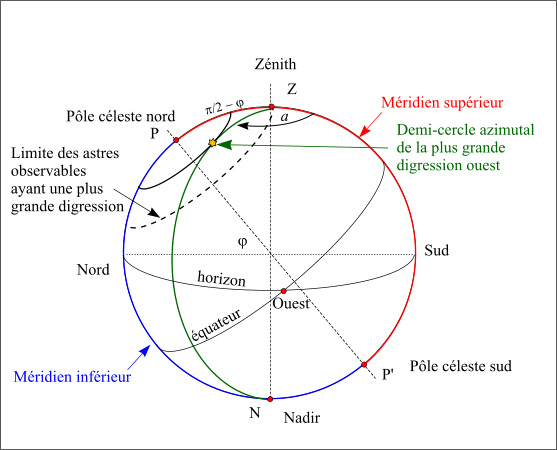
Figure 22 : Plus grande digression d'un astre.
Crédit :
ASM/Patrick Rocher
Tracer de la sphère locale dans l'hémisphère sud
On voit très souvent une représentation de la sphère céleste locale pour un lieu de l’hémisphère nord, il est intéressant de tracer également la sphère céleste locale pour un lieu de l’hémisphère sud.
Sphère locale dans l'hémisphère nord
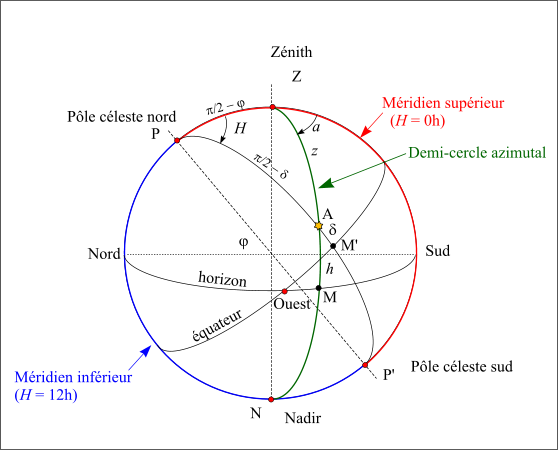
La sphère locale dans l'hémisphère nord.
Crédit :
ASM/Patrick Rocher
La sphère locale dans l'hémisphère sud
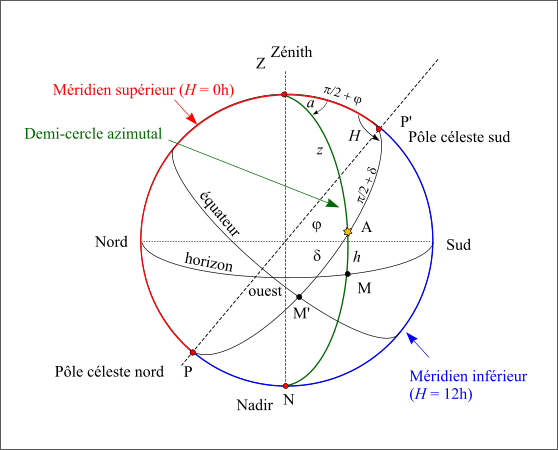
La sphère locale dans l'hémisphère sud.
Crédit :
ASM/Patrick Rocher
On remarque bien que l’angle horaire H d’un astre est croissant avec le temps que l’on soit dans l’hémisphère nord ou dans l’hémisphère sud, par contre l’azimut de l’astre (a) décroit avec le temps dans l’hémisphère sud alors qu’il croît avec le temps dans l’hémisphère nord. Ce choix de variables croissantes avec le temps est volontaire, il s'oppose à la logique mathématique qui favorise des repères directs.
Passage au méridien supérieur
Il y a deux méthodes pour étudier les conditions d’un passage au méridien supérieur, soit faire des dessins de chaque cas de figure en fonction de la latitude du lieu et déterminer les résultats par des raisonnements purement géométriques, soit utiliser une méthode analytique en regardant les résultats sur l’azimut obtenus en fixant la valeur de l’angle horaire lorsque l’astre est dans le méridien. C'est cette seconde méthode que nous allons utiliser.
Les équations ci-dessous montrent qu'on a alors deux solutions :
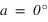 et
et 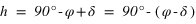 équation (1)
équation (1)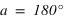 et
et 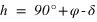 équation (2)
équation (2)
Avec la condition supplémentaire liée à la définition de la hauteur : 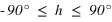 .
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si
.
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si 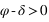 donc si
donc si 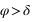 . Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si
. Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si 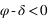 donc si
donc si 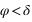 . Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors
. Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors 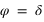 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.
Passage au méridien supérieur.
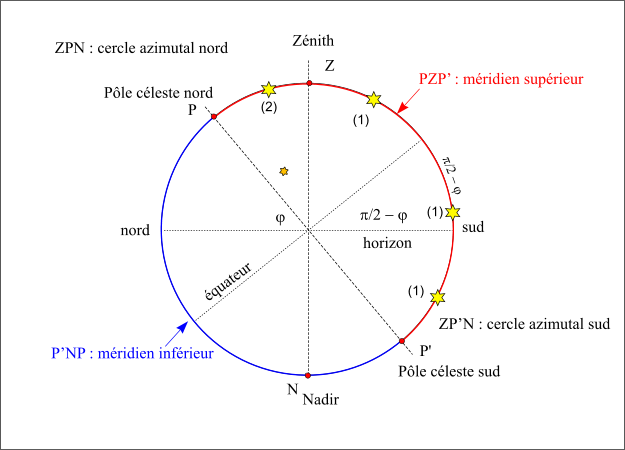
Figure 24 : Passage au méridien supérieur.
Crédit :
ASM/Patrick Rocher
Sur la figure, on a fait une coupe méridienne de la sphère céleste. Le méridien supérieur est représenté en rouge c’est le demi-cercle PZP’. L’étoile notée (2) passe au méridien supérieur avec un azimut nord (elle est sur l’arc ZPN), sa hauteur est comptée à partir de la direction nord de l’horizon.
Les autres étoiles, notées (1), passent au méridien supérieur avec un azimut sud (elles sont sur l’arc ZP’N) leurs hauteurs sont comptées à partir de la direction sud de l’horizon ; deux passent au-dessus de l’horizon, la troisième passe sous l’horizon, car une partie du méridien supérieur est sous l’horizon (sud-P’).
On remarquera aussi que la médiation de l’astre correspond à la longitude de l’écliptique qui passe au méridien en même temps que l’astre.
Exercice : Passage au méridien
Auteur: P. Rocher
 Passage du Soleil au méridien
Passage du Soleil au méridien
Difficulté : ☆☆☆
La déclinaison du Soleil varie au cours de l’année de –23° 26' 21" (au solstice d’hiver) à 23° 26' 21" (au solstice d’été) en passant par 0° (aux équinoxes).
Question 1)
Quelles sont les hauteurs du Soleil à son passage au méridien supérieur à Paris (latitude géographique : 48° 50' 11,2" N) au début de chaque saison astronomique.
On utilisera les deux solutions (1) et (2) avec la condition portant sur la hauteur, pour choisir la bonne solution.
Question 2)
Quelles sont les hauteurs du Soleil à son passage au méridien supérieur au Cap (latitude géographique : 33° 56' 0,0" S) au début de chaque saison.
Question 3)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour du solstice d’été ? Quel est le nom de ce parallèle terrestre ?
Question 4)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour du solstice d’hiver ? Quel est le nom de ce parallèle terrestre ?
Question 5)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour des équinoxes ? Quel est le nom de ce parallèle terrestre ?
Passage d'un astre au méridien inférieur
Par définition, à l'instant du passage au méridien inférieur, l'angle horaire est égale à 180° (H = 180°).
Les équations ci-dessous montrent qu'on a donc deux solutions :
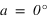 et
et 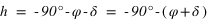 équation (3)
équation (3)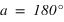 et
et 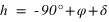 équation (4)
équation (4)
Avec toujours la condition supplémentaire : 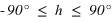 . On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si
. On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si 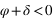 donc si
donc si 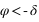 . Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si
. Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si 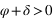 donc si
donc si 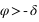 . Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors
. Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors 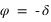 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.
Passage au méridien inférieur
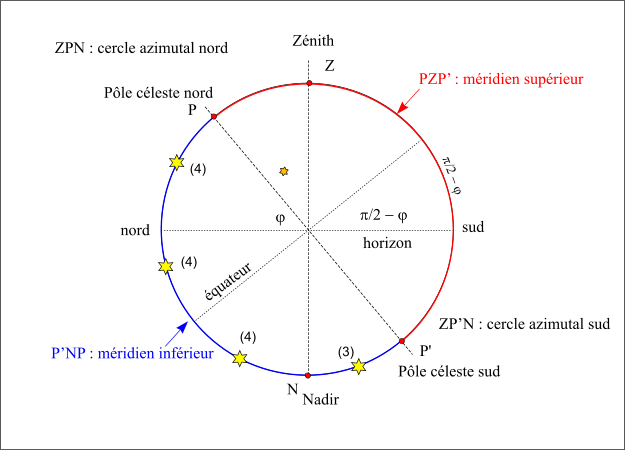
Figure 25 : Passage au méridien inférieur.
Crédit :
ASM/Patrick Rocher
Sur la figure, on a fait une coupe méridienne de la sphère céleste. Le méridien inférieur est représenté en bleu c’est le demi-cercle PNP’. L’étoile notée (3) passe au méridien inférieur avec un azimut nord (elle est sur l’arc ZP’N), sa hauteur est comptée à partir de la direction sud de l’horizon.
Les autres étoiles, notées (4), passent au méridien inférieur avec un azimut nord (elles sont sur l’arc ZPN) leurs hauteurs sont comptées à partir de la direction nord de l’horizon ; une passe au dessus de l’horizon, car une partie du méridien inférieur est au-dessus de l’horizon (nord -P), les deux autres passent sous l’horizon.
Conclusion
QCM
Applications liées au repère local-2
Auteur: Patrick Rocher
Hauteur du plan équatorial au dessus de l'horizon
Pour connaître l'angle entre le plan équatorial et le plan horizontal, on doit calculer l’intersection entre le plan équatorial et le méridien supérieur du lieu. Ce qui se traduit par une déclinaison nulle (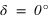 ) et le méridien supérieur => équation (1) ou (2) avec h positif.
) et le méridien supérieur => équation (1) ou (2) avec h positif.
La hauteur h obtenue avec l’équation (1) est positive (comprise entre 0° et 90°) si la latitude φ est comprise entre 0° et 90° donc dans l’hémisphère nord, la hauteur h de l’équateur sur l’horizon est égale à 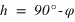 (colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
(colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
La hauteur h obtenue avec l’équation (2) est positive ou nulle (comprise entre 0° et 90°) si la latitude φ est comprise entre –90° et 0° donc dans l’hémisphère sud, la hauteur h de l’équateur sur l’horizon est égale à 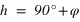 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie donc que la hauteur de l’équateur est bien le complémentaire de la latitude du lieu si le complémentaire est égal à 90° moins la valeur absolue de la latitude. De même la hauteur du pôle au-dessous de l’horizon, qui est le complémentaire de cet angle est égale à la valeur absolue de la latitude.
 Calcul de la hauteur de l'équateur
Calcul de la hauteur de l'équateur
Question 1)
Calculer la hauteur de l’équateur au méridien à Paris (latitude géographique : 48° 50' 11,2" N) et au Cap (latitude géographique : 33° 56' 0,0" S).
Hauteur du plan équatorial au dessous de l'horizon
Pour connaître l'angle entre l’équateur et le plan horizontal, on doit calculer l’intersection entre le plan équatorial et le méridien inférieur du lieu. Ce qui se traduit par une déclinaison nulle (φ = 0°) et le méridien inférieur => équation (3) ou (4) avec h négatif.
La hauteur h obtenue avec l’équation (3) est négative et comprise entre –90° et 0° si la latitude δ est comprise entre –90° et 0° donc dans l’hémisphère sud, la hauteur h de l’équateur sous l’horizon est égale à 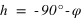 et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
La hauteur h obtenue avec l’équation (4) est négative et comprise entre -90° et 0° si la latitude δ est comprise entre 0° et 90° donc dans l’hémisphère nord, la hauteur h de l’équateur sous l’horizon est égale à 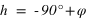 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
 Calcul de la hauteur du plan équatorial sous l'horizon
Calcul de la hauteur du plan équatorial sous l'horizon
Question 1)
Calculer la hauteur de l’équateur au dessous de l’horizon au méridien à Paris (latitude géographique : 48° 50' 11,2" N) et au Cap (latitude géographique : 33° 56' 0,0" S).
Passage du Soleil au zénith entre les tropiques
Exercice
 La déclinaison d'une étoile au zénith
La déclinaison d'une étoile au zénith
Question 1)
La direction du pôle Nord et l'équateur céleste nous fournissent des directions fixes pour toutes les sphères célestes liées aux observateurs individuels. Dans ce système de repérage, chaque étoile a sa propre déclinaison. Si, à un instant donné on voit une étoile au zénith d'un lieu particulier de latitude 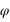 , quelle sera la déclinaison de cette étoile ?
, quelle sera la déclinaison de cette étoile ?
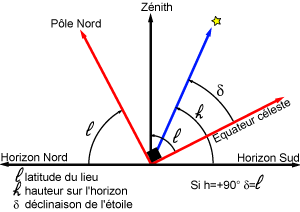
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
C'est la latitude du lieu ! Pourquoi ?
Trouver les limites des étoiles qui ne se lèvent pas
Pour un lieu quelconque de latitude φ, les étoiles qui ne se lèvent pas sont celles dont la hauteur du passage au méridien supérieur est toujours négative ou nulle.
- L’équation (1) donne
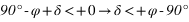
- L’équation (2) donne
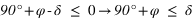
De plus la déclinaison doit toujours être comprise entre –90° et +90° donc la première inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 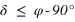 . De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant
. De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 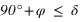 . Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
. Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
Auteur: P.Rocher
 Etoiles sous l'horizon
Etoiles sous l'horizon
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles qui ne se lèvent pas ?
Question 2)
Au Cap, en Afrique du sud (latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles qui ne se lèvent pas ?
Trouver les limites des étoiles qui ne se couchent pas
Pour qu'une étoile ne se couche pas, il faut que sa hauteur au passage au méridien inférieur soit positive ou nulle. On utilise donc les équations (3) et (4).
- L’équation (3) donne
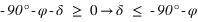
- L’équation (4) donne
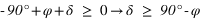
De nouveau, la déclinaison doit toujours être comprise entre –90° et +90° donc la première inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles circumpolaires doivent avoir une déclinaison vérifiant 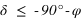 .
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant
.
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant 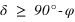 .
.
Cas particuliers : À l’équateur il n’y a aucune étoile circumpolaire. Au pôle Nord toutes les étoiles de déclinaisons positives sont circumpolaires et au pôle Sud toutes les étoiles de déclinaisons négatives sont circumpolaires.
Auteur: P. Rocher
 Exemples d'étoiles circumpolaires
Exemples d'étoiles circumpolaires
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles circumpolaires ?
Question 2)
Au Cap (Afrique du sud) (Latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles circumpolaires ?
Question 3)
Quelle est la latitude des lieux où le Soleil ne couche pas le jour du solstice d’été ? Quel est le nom de ce parallèle terrestre ? Montrer qu’en ces lieux le Soleil ne se lève pas le jour du solstice d’hiver.
Question 4)
Quels sont les lieux sur Terre où l’on voit, au cours de l’année, le plus d’étoiles ?
Question 5)
Quels sont les lieux sur Terre où l’on voit au cours de l’année le moins d’étoiles ?
Trouver les étoiles ayant une plus grande digression
On a vu que les étoiles qui ont une plus grande digression orientale ou occidentale sont les étoiles qui passent au méridien supérieur entre le zénith et le pôle.
Dans l’hémisphère nord : le passage au méridien supérieur doit se faire au nord (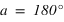 ) donc
) donc 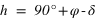 doit être inférieur à 90° donc
doit être inférieur à 90° donc 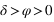 .
.
Dans l’hémisphère sud : le passage au méridien supérieur doit se faire au sud (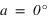 ) donc
) donc 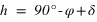 doit être inférieur à 90° donc
doit être inférieur à 90° donc 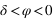 .
.
 Calcul des étoiles ayant une plus grande digression
Calcul des étoiles ayant une plus grande digression
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles qui ont une plus grande digression ?
Question 2)
Au Cap (Afrique du sud) (Latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles qui ont une plus grande digression ?
Distinction entre les étoiles circumpolaires et les étoiles ayant une plus grande digression
Il ne faut confondre étoiles circumpolaires et étoiles présentant une plus grande digression, c’est deux notions ne sont pas identiques. Par exemple dans l’hémisphère nord on a :
- Étoiles circumpolaires ⇔
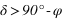 équation (1)
équation (1) - Plus grande digression ⇔
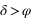 équation (2)
équation (2)
Si la latitude est supérieure à 45° la relation (2) implique (1), donc toutes les étoiles ayant une plus grande digression sont circumpolaires. Par contre, l’inverse n’est pas vrai (1) n’implique pas (2), donc toutes les circumpolaires n’ont pas forcément une plus grande digression. Par exemple pour une latitude de 50° nord, les étoiles ayant une déclinaison de 43° vérifient (1) (43°>40°), mais ne vérifient pas (2) (43°<50°).
Si la latitude est inférieure à 45°, c’est l’inverse : (1) implique (2), donc toutes les étoiles circumpolaires ont une plus grande digression, mais (2) n’implique pas (1) c’est-à-dire que toutes les étoiles ayant une plus grande digression ne sont pas forcément circumpolaires, par exemple pour une latitude de 30°, les étoiles ayant une déclinaison de 40° vérifient (2) (40°>30°), mais ne vérifient pas (1) (40°<60°).
Il y a identité entre les types d’étoiles que pour la latitude 45°.
Simulation
Pour bien comprendre les notions que nous venons de voir, on peut utliser la simulation suivante :
Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales 
Cette simulation affiche la sphère locale et la sphère équatoriale locale pour une latitude géographique φ et une longitude géographique L que l'on peut faire varier.
On peut choisir une position quelconque sur la sphère équatoriale (ascension droite α et déclinaison δ) et l'on peut faire évoluer la date et l'heure en temps universel (cela revient à faire tourner la Terre).
En bas de la simulation, on trouve les coordonnées calculées à partir des coordonnées équatoriales : angle horaire H, la hauteur h et l'azimut a.
Je vous propose de vérifier les points suivants :
- Placez-vous dans l'hémisphère nord en dehors de la bande intertropicale, à la longitude de Greenwich (L=0°,
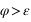 ) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.
) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h. - Placez-vous dans l'hémisphère sud en dehors de la bande intertropicale, à la longitude de Greenwich (L=0°,
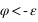 ), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.
), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h. - Pour une latitude nord proche de Paris (φ=49°), vérifier que les étoiles dont la déclinaison est supérieure à 90°-φ= 41° ne se couche pas. Vérifier que les étoiles dont la déclinaison est supérieure à 49° présentent une plus grande digression est et ouest et qu'elles passent au méridien supérieur (H=0°) et au méridien inférieur (H=12h) au nord (a=180°).Vérifier que les étoiles qui ont une déclinaison égale à la latitude du lieu passe au zénith du lieu.
- Faire la même chose avec un lieu de l'hémisphère sud.
Les nouveaux repères
Auteur: Patrick Rocher
Les nouveaux systèmes de reférence
 introduction
introduction
Nous venons de voir que le repère terrestre et le repère céleste sont liés, car on détermine les latitudes et longitudes géographiques à l’aide de mesures astronomiques (hauteur des astres et passage au méridien). Les deux repères ne sont donc pas indépendants. De plus le repère céleste écliptique dépend de la théorie du barycentre Terre-Lune et le repère équatorial dépend des théories de la précession et de la nutation.
D’où l’idée de construire de nouveaux repères indépendants. Dans la construction de ces repères on distingue le concept et sa réalisation.
 Le système de référence céleste international (ITCS) et sa réalisation (ICRF)
Le système de référence céleste international (ITCS) et sa réalisation (ICRF)
L’International Celestial Reference System (ICRS) est le concept du système de référence céleste. Ce système contient l'ensemble des prescriptions et des conventions avec les modélisations nécessaires pour définir à tout moment un repère triaxial. L’International Celestial Reference Frame (ICRF) est une réalisation de ce concept basée sur l’orientation depuis le barycentre du système solaire d’un grand nombre de radios sources extragalactiques.
 Le système de référence terrestre international (ITRS) et sa réalisation (ITRF)
Le système de référence terrestre international (ITRS) et sa réalisation (ITRF)
L’International Terrestrial Reference System (ITRS) constitue un ensemble de prescriptions et de conventions avec les modélisations nécessaires pour définir l'origine, échelle, l'orientation et l'évolution dans le temps d’un système de référence terrestre conventionnel (CTRS). L'ITRS est un système de référence idéal, défini par la résolution n°2 UGCI (adoptée à Vienne en 1991).
L’ITRF (repère terrestre international) est une réalisation du système de référence terrestre international (ITRF), obtenu à l’aide des estimations des coordonnées et des vitesses d'un ensemble de stations terrestres observées par radio interférométrie à longue base (VLBI), télémétrie laser sur la Lune (LLR), mesure GPS, télémétrie laser sur satellites (SLR) et mesures Doppler de positionnement satellitaire (DORIS).
Nouvelles méthodes de calcul
Pour l’élaboration des éphémérides terrestres des astres, on est contraint de passer des coordonnées du repère céleste (ICRF) dans des coordonnées liées à la Terre (ITRF). Ce passage se fait en deux étapes :
On passe, à l’aide de transformations relativistes strictes, dans un système céleste géocentrique sans rotation (GCRS). Puis on passe du système céleste géocentrique au système terrestre (ITRS).
La mesure des distances
Auteur: Jean-Eudes Arlot
Introduction
 Introduction
Introduction
Nous avons vu que l'astronome observe essentiellement des angles sur un ciel que l'on appelle la sphère céleste. Pourtant, tous les astres ne sont pas à la même distance de l'observateur. La Terre paraît plate et immobile. Comment, à partir de simples mesures d'angles, va-t-on pouvoir mesurer la taille de la Terre, la distance qui la sépare des astres du ciel et son mouvement dans l'espace?
Pour cela, deux notions vont être nécessaires.
La première est la notion de parallaxe : si deux observateurs voient un même objet sous deux angles différents, c'est que l'objet n'est pas à l'infini. La différence de vue ne dépend que de la position des observateurs et de la distance de l'objet observé. C'est le phénomène de relief, créé par notre cerveau à partir des images différentes reçues par nos deux yeux. Plus la distance de l'objet est grande, plus la distance entre les deux observateurs (entre les deux "yeux" qui observent) doit être grande.
La deuxième notion est celle d'un modèle théorique d'univers. On va supposer a priori des ordres de grandeur des quantités à mesurer et vérifier par l'observation et des mouvements des corps célestes. La vérification par l'observation ne sera pas une preuve que notre modèle est bon, mais qu'il colle momentanément avec l'observation. L'amélioration des mesures entraînera un écart entre l'observation et le modèle : il faudra remettre en cause celui-ci.
Comment mesurer une distance en astronomie ?
La triangulation
Commençons par essayer de mesurer la distance d'un objet situé sur la Terre. C'est ainsi que l'on pourra cartographier la surface terrestre de proche en proche.
La méthode pour mesurer une distance est celle de la triangulation : on voit un objet dans une certaine direction (visée n°1) et si on se déplace d'une distance
appelée "base", on voit l'objet dans une direction différente (visée n°2). Dans le triangle "objet - visée n°1 - visée n°2", on connaît un côté et deux angles : on
peut calculer les autres côtés et déterminer la distance de l'objet. Cet effet est appelé "parallaxe" en astronomie.
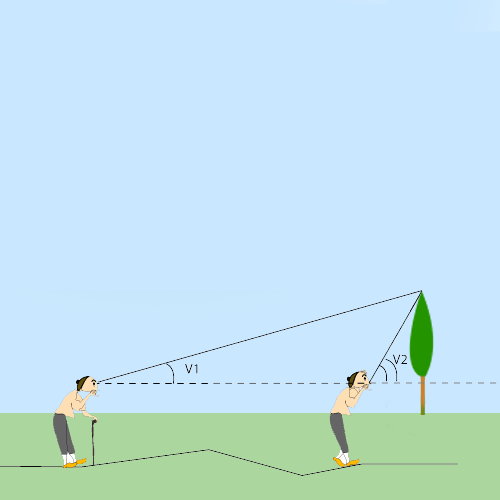
Calcul d'une distance par triangulation.
Crédit :
ASM/Jean-Eudes Arlot, Gilles Bessou et Djamila Taharbouche
La parallaxe en astronomie
Pour calculer la distance d'un corps céleste à la Terre, on procédera de la même façon. Depuis deux lieux sur Terre, on va mesurer l'angle de vue d'un astre et, connaissant la base, calculer la distance.
On conçoit bien que cette méthode a ses limites : si l'astre est très loin, la plus grande base terrestre ne pouvant dépasser 12000 kilomètres (le diamètre terrestre), il faut que la différence d'angle de visée entre les deux observateurs soit mesurable avec l'instrumentation dont les astronomes disposent. Jusqu'au XVIIème siècle, même la distance de la Lune n'était pas accessible par cette méthode.
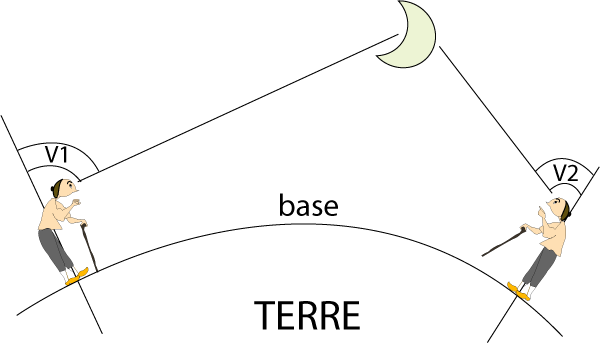
Calcul d'une distance par parallaxe.
Crédit :
ASM/Jean-Eudes Arlot, Gilles Bessou et Djamila Taharbouche
Exercice
 Calcul d'une distance par triangulation
Calcul d'une distance par triangulation
Mesure de distance par triangulation
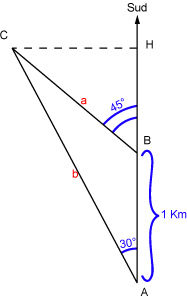
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
Question 1)
On désire mesurer la distance CH entre un bâtiment C et une route ABH de direction Nord-Sud sur laquelle se déplace un observateur qui ne peut mesurer que des angles ou des distances sur la route. D'une position A, l'observateur mesure un angle d'azimuth 30° entre le bâtiment C et la direction du Sud. D'une position B située un kilomètre plus loin sur la route, l'observateur va mesurer un azimuth de 45°.
Pour calculer la distance CH, il suffit de résoudre le triangle ABC connaissant les deux angles en A et B et la base AB. On applique une des relations entre angles et côtés dans un triangle.
Rappel : dans un triangle quelconque ABC, on a la relation :
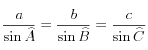
La mesure par la parallaxe
L'image ci-contre montre le principe de détermination de la distance Terre-Lune par la parallaxe (on connaît D et le rayon terrestre et on mesure α et β). Comme nous l'avons vu précédemment, il est impératif de disposer d'instruments capables de mesurer une différence entre les angles α et β. Cela limite la distance à la Terre mesurable.
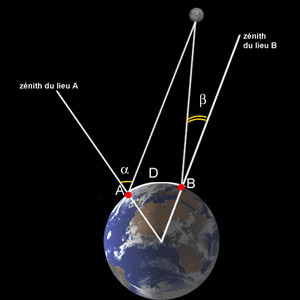
Principe de la mesure de la distance Terre-Lune par triangulation
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou + images NASA
En savoir plus: la parallaxe horizontale
 En savoir plus
En savoir plus
On a vu précédemment que triangulation ou parallaxe utilisait le même principe pour déterminer la distance d'un objet éloigné sans avoir à y aller et sans mesurer directement la distance à l'objet. On remarque que la précision de la mesure dépend de la longueur de la base. Il faut pouvoir mesurer les angles avec suffisamment de précision. Pour un astre pas trop éloigné, il suffit de se déplacer sur la surface de la Terre -ou mieux de faire deux observations simultanées à partir de deux lieux éloignés sur la surface de la Terre- pour en déterminer la distance. C'est tout à fait faisable pour la Lune qui est proche avec nos instruments de mesure actuels.
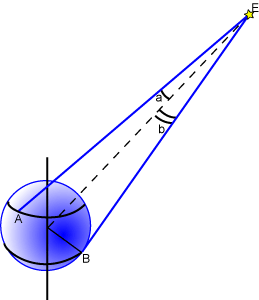
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
On remarque alors que le mouvement diurne de rotation de la Terre autour de son axe déplace chaque observateur au cours de la journée. Ce déplacement va modifier l'angle sous lequel on voit un astre à distance finie par rapport à l'angle de vue depuis le centre de la Terre qui ne bouge pas. C'est la parallaxe diurne. La distance séparant deux positions d'un observateur peut servir de "base" pour mesurer une distance. Cependant, une telle base a une valeur limite maximale : c'est le diamètre terrestre.
On appellera "parallaxe horizontale d'un astre", la valeur maximale de la parallaxe diurne de cet astre. Elle sera atteinte pour un astre observé à l'horizon. Cette valeur est donc l'angle sous lequel un observateur situé sur l'astre en question voit le rayon terrestre.
On verra plus loin que le déplacement de la Terre autour du Soleil va servir de base pour la parallaxe annuelle.
Mesure de la distance Terre-Soleil et Terre-Planètes
La méthode de triangulation précédente devrait pouvoir être appliquée à tous les corps du système solaire. Mais pour le Soleil, c'est très difficile : il n'est pas facile à observer et il est beaucoup plus loin que la Lune (400 fois, voir figure). Pour le Soleil et les objets du système solaire éloignés, on ne peut pas appliquer simplement la méthode des parallaxes car les mesures précises d'angles ont des limites : il faut prendre en compte la réalisation des mesures pour laquelle la grandeur de la base n'est pas forcément suffisante. Le principe de la parallaxe et du calcul de triangulation est simple mais il n'est pas applicable aux astres éloignés. Nous verrons que nous aurons besoin d'un nouveau modèle théorique pour mesurer certaines distances et en déduire celles qui ne
sont pas accessibles directement à la mesure. Les lois de Kepler et la mécanique céleste seront nécessaires pour la détermination des distances dans le système solaire.

Crédit :
CNRS/Jean-Eudes Arlot
La nécessité d'un modèle théorique en astronomie
Le principe de mesure de distance présenté dans la section précédente n'est pas suffisant pour connaître toutes les distances dans le système solaire, loin de là. En effet, ce principe appliqué naïvement au Soleil en supposant que la Terre est plate, nous donne une distance du Soleil à la Terre de 6500 kilomètres !
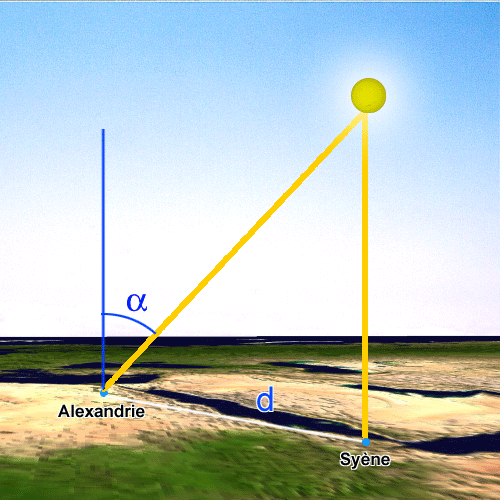
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou + image NASA
Ce type de mesure a probablement été réalisé dans l'antiquité. Anaxagore (4ème siècle avant J.-C.) calcule une taille d'environ 60 kilomètres pour le Soleil, ce qui le met à 6500 kilomètres de la Terre. Il a donc fait un calcul sur une base fausse. Pour calculer les distances dans le système solaire, il faut donc avoir de bonnes hypothèses, c'est-à-dire un modèle théorique de ce que l'on cherche à mesurer.
Premier modèle indispensable : la Terre est ronde et le Soleil est loin...
Exercice
 Calcul d'une distance par triangulation
Calcul d'une distance par triangulation
Question 1)
Expliquer en détail le raisonnement supposé d'Anaxagore qui lui fait dire que le Soleil est à 6500km et qu'il mesure environ 60 kilomètres de diamètre.
La distance Alexandrie-Syène est de 5000 stades soit 800 km. L'angle zénith-observateur-Soleil mesuré depuis Alexandrie est de 7°.
Le diamètre apparent du soleil est 0,5°.
La mesure de la Terre
Comment mesurer la Terre et constater qu'elle est ronde ? Sa rotondité est facilement compréhensible et deux faits avaient amené les astronomes de l'antiquité à admettre cette rotondité. D'abord, lors de l'observation des éclipses de Lune, l'ombre de la Terre est circulaire. Mais cette constatation pouvait aussi bien signifier que la Terre était plate avec une forme de disque. C'est la disparition progressive des navires sous l'horizon qui suggère bien que la Terre
est ronde. Comment maintenant mesurer le rayon de la Terre ?
La première mesure a été celle d'Eratosthène (vers 285-194 avant J.C.) durant l'antiquité grecque. Il avait constaté que les rayons du Soleil étaient parallèles, du moins que le Soleil était très loin sinon à l'infini. Il avait constaté que le jour du solstice, à midi, les objets n'avaient pas d'ombre à Syène (aujourd'hui Assouan) et que l'on pouvait observer le Soleil au fond d'un puits. Ce phénomène n'avait pas lieu à Alexandrie 800 km plus au Nord. Eratosthène mesura donc l'ombre portée d'un bâton à Alexandrie le jour du solstice . Il lui fallait aussi mesurer la distance Alexandrie-Syène (5000 stades) ce qui n'allait pas de soi à cette époque. Cette mesure n'était pas interprétée comme un calcul de triangulation prouvant que le Soleil était proche car il fallait se déplacer dans la direction Nord-Sud pour constater un changement de direction du Soleil. Une mesure à la même heure solaire locale (la seule disponible à l'époque) pour des lieux situés sur une ligne Est-Ouest n'aurait rien donnée (d'où la supposition que les rayons du Soleil étaient parallèles). Eratosthène ne se trompa que d'un centième sur la taille de la Terre.
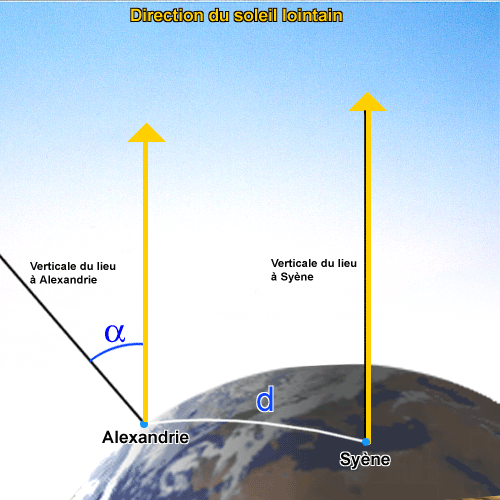
Principe des premières mesures de la taille de la Terre : le Soleil n'est pas à l'infini, mais il est suffisamment loin pour que la valeur ainsi obtenue soit très proche de la réalité
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou + image NASA
Passage d'un angle apparent à une distance
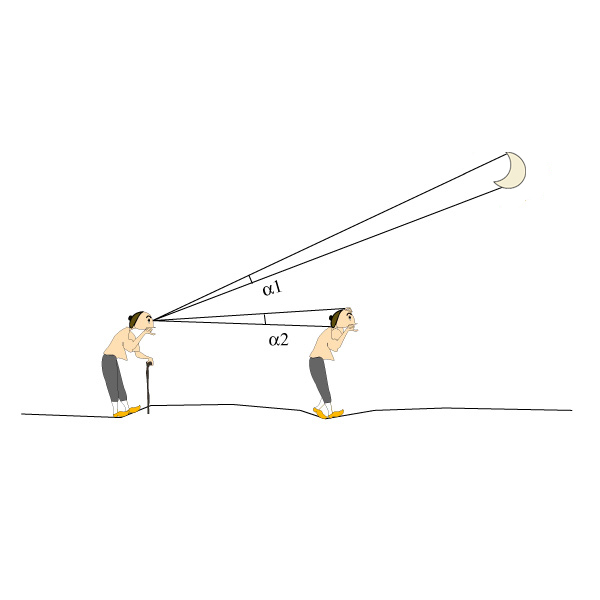
Crédit :
ASM/Jean-Eudes Arlot, Gilles Bessou et Djamila Taharbouche
Si les deux angles α1 et α2 sont égaux, peut-on en déduire que la dimension de la Lune et celle de la tête du deuxième personnage est la même ?
Non, bien sûr...
Par contre, si α1=α2, alors distances et tailles sont liées entre elles grâce au théorème de Thalès.
Exercice
 Les distances dans le système solaire
Les distances dans le système solaire
Question 1)
La Lune et le Soleil ont à peu près le même diamètre apparent. Sachant que la Lune a un diamètre de 3475 km et se trouve à 384400 km de la Terre, quel est le diamètre du Soleil sachant qu'il se trouve à 149 600 000 km de la Terre.
Appliquer le théorème de Thalès.
La distance Terre-Lune
La mesure de la distance Terre-Lune par les éclipses
La première mesure de la taille de la Lune et de la distance Terre-Lune a été réalisée dans l'antiquité au moyen de l'observation des éclipses. L'observation des éclipses de Lune montre la largeur de l'ombre de la Terre sur la Lune et on voit que le diamètre de l'ombre de la Terre est de 2,5 diamètres lunaires au niveau de la Lune. Or, lors d'une éclipse de Soleil, la surface terrestre est au sommet du cône d'ombre puisque la zone de la Terre dans l'ombre est petite (les diamètres apparents de la Lune et du Soleil sont quasi-identiques). L'ombre de la Lune s'est donc rétrécie d'un diamètre lunaire après la distance Terre-Lune.
Il doit en être de même pour l'ombre de la Terre sur la Lune. Donc la Terre fait 2,5+1=3,5 diamètres lunaires. Connaissant le diamètre terrestre on en déduit le diamètre lunaire en kilomètres. L'angle selon lequel on voit la Lune étant d'un demi-degré (1/110 radian), la distance Terre-Lune est donc de 110 diamètres lunaires soit 60 rayons terrestres soit 384 000 km.
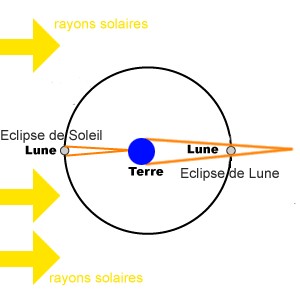
Principe de la mesure de la taille de la Lune et de la distance Terre-Lune grâce aux éclipses
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
Les lois de Kepler
Auteur: Jean-Eudes Arlot
Introduction
 Introduction
Introduction
L'observation du ciel n'est pas suffisante pour bien appréhender les distances des astres et comprendre le mécanisme de leur mouvement. L'observation va permettre de valider les principes théoriques qui ne seront tout d'abord que des suppositions. Les lois que Kepler va énoncer seront validées par l'observation.
L'héliocentrisme
Pourquoi l'héliocentrisme ?
Jusqu'à Copernic et Galilée, on suppose la Terre immobile au centre de l'univers. Effectivement, aucune observation ne peut mettre en évidence un mouvement de la Terre dans l'espace. Copernic et Galilée vont supposer le mouvement des planètes autour du Soleil. Kepler va énoncer des lois pour ce mouvement, lois qui ne découlent que de l'observation du mouvement des astres. Ces lois ne représentent qu'une description cinématique de ce mouvement sans faire d'hypothèses sur la nature des forces en jeu.
Kepler (1571-1630) est le disciple de Tycho Brahe (1546-1601) auquel il succède comme astronome de l'empereur d'Allemagne Rodolphe II. Tycho Brahe est principalement un observateur de positions précises mais s'il effectue de très bonnes observations, en revanche, il n'est pas convaincu par les théories héliocentriques de Copernic (1473-1543). Il pense toujours que la Terre est au centre du système solaire. Kepler va utiliser les observations de Tycho Brahe pour énoncer ses lois. Kepler est convaincu que Copernic a raison, ce qui sera définitivement admis après Galilée (1564-1642) en 1610 grâce à l'utilisation d'une lunette astronomique et à l'observation des satellites de Jupiter.
Kepler énonce ses deux premières lois en 1609 et sa troisième loi en 1619.

Kepler (1571-1630)
Crédit :
Danielle Briot - Collection particulière
Histoire : de la Terre plate aux orbites elliptiques
Il a fallu plus de deux mille ans pour comprendre que les planètes avaient des orbites elliptiques autour du Soleil. La progression des connaissances ne fut pas régulière, loin de là !
On doit la première démarche scientifique de recherche d'une représentation de l'univers à Thalès (625-547 avant J.-C.). Il fonda, au 6ème siècle avant notre ère, l'école des philosophes ioniens à Milet. La Terre était alors supposée de forme géométrique plate. L'un des disciples de Thalès, Anaximandre (610-547 avant J.-C.), supposa une Terre cylindrique habitée sur sa partie supérieure plane. C'est à cette époque que la notion de sphères célestes supportant les corps célestes apparaît : cette notion perdurera jusqu'au Moyen Âge.
Vers la même époque, à l'école de Pythagore (570-480 avant J.-C.) on affirma la sphéricité de la Terre, celle du Soleil et de la Lune en étant un indice. Toutes les formes et les mouvements célestes se devaient d'être parfaits, donc sphériques ou circulaires : le philosophe pythagoricien Parménide (543-449 avant J.-C.) fut le premier à exprimer la sphéricité de la Terre ainsi que le fait que la Lune était éclairée par le Soleil..
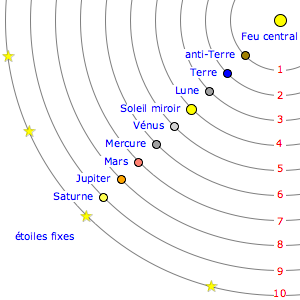
Le monde selon Philolaos (470-400 avant J.-C.)
Crédit : ASM/Damien Guillaume
Histoire : le monde d'Aristote
Aristote (384-322 avant J.-C.), disciple de Platon, précepteur d'Alexandre le Grand, peut sans doute être considéré comme le plus grand savant de l'Antiquité. Son oeuvre colossale, composée de plusieurs dizaines de volumes, abordera aussi bien l'astronomie, la physique que la botanique ou la médecine. Aristote va en particulier développer un modèle physique, fondé sur l'observation et la perception intuitive des phénomènes, dont l'influence sera déterminante pour les siècles à venir. Sa conception de l'Univers est basée sur 3 dogmes fondamentaux :
- la Terre est immobile au centre de l'Univers
- il y a séparation absolue ente le monde terrestre imparfait et changeant et le monde céleste parfait et éternel (la limite étant l'orbite de la Lune)
- les seuls mouvements célestes possibles sont les mouvements circulaires uniformes.
La Terre immobile est faite des quatre éléments eau, air, terre et feu. Aristote pense même avoir "démontré" l'immobilité de la Terre avec un argument basé sur le fait que si la Terre était en mouvement nous devrions en ressentir directement les effets. Pour ce qui est de la mécanique céleste, Aristote considérera un système de sphères centrées sur la Terre. La sphère extérieure est celle des fixes. Ce système présentait cependant un défaut majeur, qui sera mis en évidence au siècle suivant. S'il rendait en effet compte à peu près correctement des mouvements des planètes, il ne pouvait expliquer leurs variations d'éclat au cours de l'année, car dans ce modèle les planètes étaient supposées à une distance constante de la Terre. Certes, Aristote aurait pu invoquer une variation intrinsèque de l'éclat des planètes, mais cela était incompatible avec son dogme sur la perfection et l'immuabilité des cieux.
Le monde d'Aristote
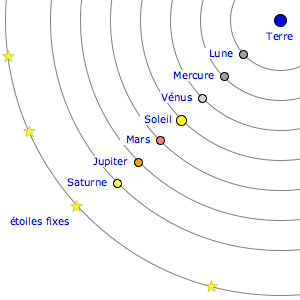
Le système d’Aristote
Crédit : ASM/Damien Guillaume
Histoire : les premières mesures
Il semble qu'au 4ème siècle avant notre ère, Héraclide du Pont (388-310 avant J.-C.) envisagea que la sphère des fixes était immobile et que la Terre tournait autour de son axe, ce qui expliquerait le mouvement diurne des étoiles (mais les sources écrites sont ici très ténues et incertaines).
Au 3ème siècle avant notre ère Eratosthène (284-192 avant J.-C.) fit la première mesure précise du rayon terrestre : il utilisa le fait que l'ombre portée d'un bâton à midi faisait 7° 10' le jour du solstice à Alexandrie alors qu'elle était nulle (le Soleil était au zénith) 800 kilomètres plus au sud à Syène sur le tropique du Cancer. Ce fut le premier calcul mathématique de mesure dans le système solaire. Il trouva ainsi 6500 kilomètres pour le rayon terrestre, soit une valeur remarquablement correcte.
A la même époque vécut Aristarque de Samos (310-230 avant J.-C.), dont l'œuvre est attestée par très peu de traces écrites. Il fut sans doute un des premiers à estimer (avec une remarquable précision) la distance Terre-Lune. Aristarque est par ailleurs crédité pour avoir proposé un modèle héliocentrique du monde (mais le seul témoignage écrit est une phrase d'un manuscrit d'Archimède).
Au 2ème siècle avant notre ère vécut Hipparque (190-120 avant J.-C.), peut-être le plus grand astronome de l'Antiquité. Hipparque fut avant tout un grand observateur. Il mis en évidence le phénomène de précession des équinoxes, qu'il estima être de 36 secondes d'arc par an (la vraie valeur est de 50 secondes). Hipparque calcula également assez précisément la longueur de l'année tropique : 365 jours 5 heures 55 minutes 12 secondes (la vraie valeur était 365 jours 5 heures 48 minutes 46 secondes).
Histoire : l'univers de Ptolémée
L'astronomie grecque va connaître son apogée au 2ème siècle de notre ère avec l'astronome alexandrin Claude Ptolémée (100-170). Ptolémée va faire la synthèse de tous les travaux de ses prédécesseurs (en particulier Hipparque) et va les parachever en proposant un système physique et mathématique du ciel qui restera incontesté pendant près de 14 siècles. Tous les travaux astronomiques de Ptolémée sont quasiment regroupés dans un seul ouvrage majeur, la "grande syntaxe mathématique", plus connu sous le nom que lui donnèrent les Arabes : l'Almageste. L'Almageste reprend dans ses grandes lignes la vision aristotélicienne du monde physique, avec les mêmes dogmes et principes : dichotomie Terre/Univers, immobilité de la Terre, etc.
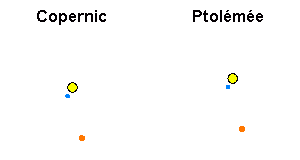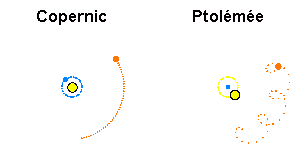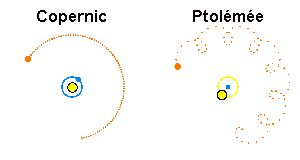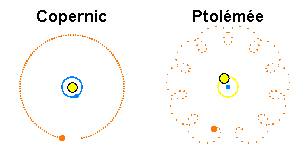
Crédit : ASM/Benoît Mosser
Histoire : l'héliocentrisme de Copernic
Nicolas Copernic (1473-1543), un chanoine et astronome polonais, va remettre en cause le modèle géocentrique du monde de Ptolémée et d'Aristote dans un ouvrage publié l'année de sa mort : le "De Revolutionibus orbium caelestium". Cet ouvrage propose un modèle héliocentrique du monde, dans lequel tous les mouvements planétaires sont centrés sur le Soleil. Mais surtout, ce que Copernic va affirmer c'est que la Terre n'est ni immobile, ni au centre du monde. Elle est en effet animée de 2 mouvements : l'un sur elle-même en 24h (qui remplace le mouvement de la sphère des fixes des Grecs anciens) et l'autre autour du Soleil en un an, faisant de la Terre une planète comme les autres. Contrairement à ce que l'on croit parfois, Copernic ne va pas démontrer l'héliocentrisme, car il faudra attendre plus de 150 ans pour avoir une preuve du mouvement de la Terre. L'argument de Copernic est que son modèle est plus simple, plus logique et plus "harmonieux" que celui de Ptolémée (même si dans le détail le fonctionnement mathématique du système copernicien est assez complexe).
Le De Revolutionibus, malgré son côté fondamentalement révolutionnaire, fut reçu avec relativement d'indifférence par les savants de l'époque.
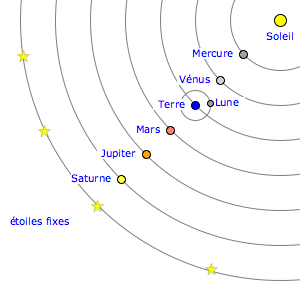
Le système héliocentrique de Copernic
Crédit : ASM/Damien Guillaume
Histoire : le géohéliocentrisme de Tycho-Brahe
Tycho Brahe (1546-1601) fut avant tout un observateur hors pair. Il construisit ses instruments lui permettant d'atteindre une précision de mesure inégalée (2 minutes de degré). Il effectua des observations continues du Soleil, de la Lune, des planètes et des étoiles pendant trente ans et constata les erreurs des tables d'éphémérides de l'époque. Il observa la supernova de 1572 ce qui sera le point de départ de la remise en cause de l'immuabilité de la sphère des fixes d'Aristote et de Ptolémée. Il observa une comète en 1577 et, là aussi, il prit en défaut les théories d'Aristote : la comète n'appartenait pas au monde sublunaire et son orbite coupait celles des autres planètes. Il ne put mesurer de parallaxe annuelle des étoiles, ce qui lui fit adopter le système géohéliocentrique.
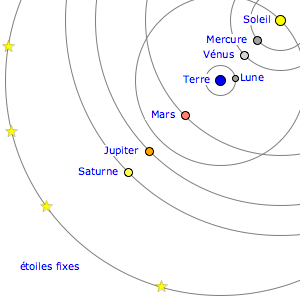
Le système de Tycho Brahe
Crédit : ASM/Damien Guillaume
Giordano Bruno (1548-1600) était plus un philosophe qu'un astronome mais il introduisit une vision du monde fondée sur un univers infini qui tranchait avec les idées admises alors. Il défendit aussi l'idée de la pluralité des mondes habités autour des étoiles et celle que la Terre n'était pas le centre de l'univers, pas plus que le Soleil. Il se heurta à l'Inquisition, ce qui n'était pas prudent à l'époque.
Histoire : les orbites elliptiques autour du soleil
Johannes Kepler (1571-1630), très grand calculateur et mathématicien, eut la chance de prendre la suite de Tycho Brahe dont il analysa les observations. Kepler fut capable d'en déduire les orbites des planètes et d'énoncer les lois qui portent son nom et qui caractérisent ces orbites. Il introduisit pour la première fois la notion d'orbite elliptique, rompant avec les sacro-saints mouvements circulaires uniformes érigés en dogme par les Grecs. Kepler montra par ailleurs que les plans des orbites planétaires passaient par le Soleil et non par la Terre, ce qui contredisait un des postulats du géocentrisme.
Galilée (1564-1642) était d'abord un physicien et il étudia la mécanique et la dynamique des corps en mouvement. Galilée établit la loi de l'inertie (tout corps non soumis à une force extérieure est animé d'un mouvement rectiligne uniforme et se trouve dans un référentiel que l'on nomme aujourd'hui "galiléen"). C'est à la fin de l'année 1609 et au début de 1610 qu'il a l'idée de braquer une lunette d'approche récemment inventée et qu'il a construit lui-même vers le ciel. Ses découvertes seront nombreuses et vont bouleverser la vision de l'univers de l'époque. Il observa des taches sur le Soleil, des cratères sur la Lune, les phases de Vénus, une multitude d'étoiles dans la Voie lactée et des satellites autour de Jupiter. Cette dernière découverte donnait le coup de grâce au géocentrisme. Il adhéra aux idées de Copernic et à l'héliocentrisme sans pouvoir le démontrer et ne considéra pas le géohéliocentrisme qui nous semble aujourd'hui être une étape incontournable dans l'élaboration d'un modèle d'univers.

Crédit :
Danielle Briot - Collection particulière
Ainsi, au début du XVIIème siècle, on avait une vision de l'univers assez proche de la réalité. Cependant, on ignorait complètement comment les mouvements observés pouvaient se faire. Il faudra attendre Newton et la gravitation
universelle et la mécanique céleste pour pouvoir décrire tous ces mouvements par des théories dynamiques et non plus de simples modèles cinématiques.
QCM
Les trois lois de Kepler
La première loi de Kepler
Chaque planète décrit, dans le sens direct, une ellipse dont le Soleil occupe l'un des foyers.
Jusqu'alors, on n'avait considéré que le cercle comme trajectoire possible des corps célestes. Ce sont les observations précises de Tycho Brahe qui ont permis de revenir sur ce postulat. L'ellipticité des orbites des planètes est très faible. La différence entre le cercle et l'orbite de la Terre est infime : si on veut la représenter sur une feuille de papier, la différence entre le cercle et l'ellipse tient dans l'épaisseur du trait de crayon ! Heureusement le Soleil n'est pas au centre de l'ellipse, mais au foyer qui est décentré.
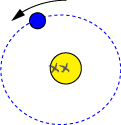
Orbite de la Terre : une ellipse peu excentrique dont le Soleil occupe un des foyers.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
Cas d'une orbite très excentrique
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
La deuxième loi de Kepler
Les aires décrites par le rayon vecteur planète-Soleil sont proportionnelles aux temps employés pour les décrire.
La signification de cette loi est claire : les planètes ne tournent pas avec une vitesse uniforme ; elles vont plus vite quand elles sont près du Soleil et plus lentement quand elles en sont loin. Cela est particulièrement observable pour les comètes dont les orbites sont, contrairement à celles des planètes, très excentriques (très allongées).

La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales.
Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitesse diminue.
Crédit : ASM/Benoît Mosser
La troisième loi de Kepler
Le cube du demi grand axe "a" d'une orbite d'une planète, divisé par le carré de la période de révolution sidérale "T" est une constante pour toutes les planètes du système solaire.
C'est-à-dire :
a3/T2 = constante
ou bien n2 a3 = constante
(n étant le moyen mouvement = 2π/T)
Cette loi relie les planètes entre elles. En fait, cette loi provient de la masse prépondérante du Soleil dans le système solaire. On verra que la loi de la gravitation engendre une force proportionnelle aux masses en jeu. Dans le cas du système solaire, les masses des planètes sont négligeables devant celle du Soleil et la constante ci-dessus est le produit de la masse solaire et de la constante de la gravitation.
Kepler ne pouvait pas démontrer ses lois : il lui manquait les principes fondamentaux de la mécanique ainsi que la loi de Newton, c'est-à-dire les fondements de la dynamique, qui, appliqués aux astres, forment la mécanique céleste. Kepler introduit la notion de trajectoire elliptique qui va complètement modifier la modélisation du système solaire.
Exercice
 Calcul du demi grand axe d'Uranus
Calcul du demi grand axe d'Uranus
Question 1)
Calculer le demi-grand axe de l'orbite d'Uranus connaissant les paramètres de l'orbite terrestre et sachant que la période de révolution d'Uranus autour du Soleil est de 84 ans.
Appliquer la troisième loi de Kepler pour des corps tournant autour du Soleil
Exercice
 Distance minimale Terre-Saturne
Distance minimale Terre-Saturne
Question 1)
Calculez la distance minimale Terre-Saturne
connaissant la période orbitale de Saturne (29,5 ans). On
supposera les orbites dans le système solaire circulaires.
1 unité astronomique égale (environ): 150 millions de km,
c'est le demi grand axe de la Terre
sa période de révolution est un an
Calculer tout d'abord le demi-grand axe de Saturne
En savoir plus: les paramètres de l'ellipse
Les distances dans le système solaire
Parallaxe diurne, parallaxe horizontale
On a vu précédemment que triangulation ou parallaxe utilisait le même principe pour déterminer la distance d'un objet éloigné sans avoir à y aller et sans mesurer directement la distance à l'objet. On remarque que la précision de la mesure dépend de la longueur de la base. Il faut pouvoir mesurer les angles avec suffisamment de précision. Pour un astre pas trop éloigné, il suffit de se déplacer sur la surface de la Terre -ou mieux de faire deux observations simultanées à partir de deux lieux éloignés sur la surface de la Terre- pour en déterminer la distance.
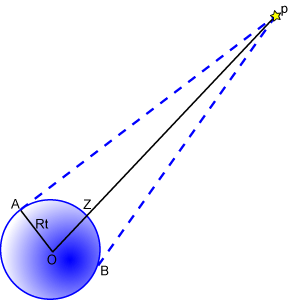
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
La parallaxe diurne a une valeur maximale : c'est la "parallaxe horizontale" pour un astre donné (quand l'observateur est en A). Elle sera atteinte pour un astre observé à l'horizon. Cette valeur est donc l'angle sous lequel un observateur situé sur l'astre P en question voit le rayon terrestre RT. La parallaxe diurne est nulle lorsque l'astre observé est au zénith (observateur en Z, sur la droite OP).
La troisième loi de Képler
Ayant vu comment les astronomes mesurent les distances aux astres lointains -mais pas trop-, comment va-t-on concrètement mesurer le système solaire tout entier ? Le Soleil est bien trop loin pour qu'une mesure de parallaxe nous en donne sa distance. Les lois de Kepler vont nous donner les rapports des distances des planètes au Soleil et il suffira de connaître une seule distance entre les planètes pour les connaître toutes.
La première loi de Kepler énonce que les orbites des planètes autour du Soleil sont des ellipses.
La deuxième loi de Kepler est la loi des aires. Plus simplement, elle indique les planètes vont plus vite sur leur orbite quand elles sont près du Soleil. Nous utiliserons cette loi pour l'analyse des observations de passage qui nécessite de connaître la vitesse angulaire apparente de Vénus sur le disque solaire.
La troisième loi de Kepler nous fournit les rapports entre les distances au Soleil de toutes les planètes et il suffit ainsi de connaître une seule distance dans le système solaire pour connaître toutes les autres. Elle s'énonce ainsi :
le rapport a3/T2 est constant pour toutes les planètes du système solaire où a est le demi grand axe de l'orbite et T la période de révolution autour du Soleil. La figure ci-dessous montre ce qui se passe si les orbites sont des cercles, connaissant la distance Δ et les périodes t1 et t2.
La première loi de Kepler énonce le fait que les orbites sont des ellipses et on ne pourra donc pas assimiler les distances Soleil-Terre et Soleil-Vénus aux demi-grands axes aT et aV des orbites de la Terre et de Vénus. On passe du demi grand axe "a" à la distance Soleil-planète (rayon vecteur) "rP" par la formule :
rP = a (1 - e cos E) où e est l'excentricité de l'ellipse et E caractérise l'emplacement de la planète sur son orbite elliptique (E est appelé "anomalie excentrique").
La distance Terre-Mars
Pour mesurer le système solaire, il nous suffit donc de mesurer une distance entre la Terre et la planète la plus proche. Dès le XVIIème siècle, on s'est tourné vers Mars et Vénus qui passent régulièrement à une distance pas trop grande de la Terre.
Pour comprendre comment mesurer leur distance à la Terre, voyons concrètement comment en déterminer la parallaxe.
On a vu qu'il fallait mesurer un angle de visée d'un astre par rapport à une direction fixe, connue des deux observateurs, même éloignés et sans contact. Cette direction fixe va être fournie par un astre situé à proximité de l'astre dont on veut mesurer la distance, mais situé suffisamment loin pour pouvoir être considéré comme étant à l'infini. Cela revient à dire que sa parallaxe est nulle : quel que soit le lieu de la Terre d'où on l'observe, on le voit toujours dans la même direction. On va donc utiliser les étoiles pour lesquelles la parallaxe diurne est négligeable. On a appliqué cette méthode à la planète Mars dès le XVIIème siècle mais la visée des étoiles était difficile et on a cherché un autre astre et une méthode plus facile.
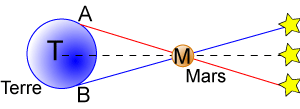
Cas de la planète Mars : celle-ci n'apparaît pas devant les mêmes étoiles selon le lieu d'observation sur Terre
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
Pour la planète Mars, seul le principe de la parallaxe avec un calcul utilisant une base connue (dépendant des lieux d'observation sur Terre) va nous permettre de calculer la distance Terre Mars.
La distance Terre-Vénus
La planète Vénus, passant régulièrement devant le Soleil, a apporté une bonne solution. Lors d'un tel passage, le disque solaire est un repère sur lequel la planète Vénus va apparaître à des endroits différents pour des observateurs différents. C'est le principe de la parallaxe.
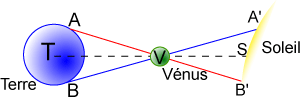
Cas de la planète Vénus : la projection de son disque sombre sur le disque solaire lors d'un passage n'est pas la même pour deux observateurs terrestres
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
Pour Vénus, on se sert du Soleil comme référence pour calculer la parallaxe. A la différence du calcul de la parallaxe pour la planète Mars, le Soleil n'est pas à l'infini : il a lui aussi une parallaxe et il nous faut connaître le rapport des distances du Soleil à Vénus et à la Terre. Cela nous est fourni par les lois de Kepler. On connaît la distance AB, l'angle en V (par l'observation) ainsi que le rapport VA/VA' (par la troisième loi de Kepler), on en déduit VT, VS et TS, d'où la distance Terre-Soleil et l'unité astronomique. Le problème se complique du fait que A et B bouge (rotation de la Terre autour de son axe), ainsi que T et V (révolution de la Terre et de Vénus autour du Soleil).
Dès le XVIIIème siècle, la distance Terre-Soleil était connue assez précisément : 150 millions de kilomètres environ que l’on nommera l’unité astronomique, unité de mesure du système solaire.
QCM
La mécanique céleste
Auteur: Jean-Eudes Arlot
Introduction
 Introduction
Introduction
Les lois de Kepler ne sont qu'une description empirique cinématique de ce que l'on observe. En fait, le mouvement des astres est régi par des principes plus fondamentaux qui vont permettre d'expliquer de nombreux phénomènes: ce sont les principes de la mécanique céleste.
Dynamique et gravitation
Le principe fondamental de la dynamique
Le principe fondamental de la dynamique est un outil développé dans le cadre de la mécanique classique, qui permet de faire le lien entre les forces appliquées à un corps et l'évolution cinématique de ce corps. Appliqué à un solide de masse m dont le mouvement est défini dans un référentiel dit galiléen, le principe s'énonce :
F = m γ = m dv / dt
F représente l'ensemble des forces appliquées à l'objet, et γ son accélération. dv / dt est la dérivée de la vitesse par rapport au temps (soit l'accélération).
En savoir plus: le principe fondamental de la mécanique
 En savoir plus
En savoir plus
Appliquée à un point matériel (un solide de dimension négligeable devant les distances mises en jeu) ou à un ensemble de points matériels, cette loi peut se réécrire de diverses manières, toutes équivalentes :
- le théorème du mouvement du centre de masse (ou barycentre) :
"le barycentre d'un système matériel se meut comme si toute la masse du système y était transportée, les forces extérieures au système agissant toutes sur ce barycentre"
- le théorème du moment cinétique appliqué à un point matériel :
"la dérivée par rapport au temps du moment cinétique en un point d'un système matériel est, à chaque instant, égale au moment résultant des forces extérieures par rapport à ce même point"
- le théorème de l'énergie cinétique (autrefois appelé théorème des forces vives) :
"la variation de l'énergie cinétique d'un système matériel pendant un intervalle de temps donné est égal à la somme des travaux des forces intérieures et extérieures appliquées à ce système pendant cet intervalle de temps".
Notons que du théorème du moment cinétique découle directement la deuxième loi de Kepler (lois des aires), résultant du seul fait que l'interaction gravitationnelle est une force "centrale".
Histoire : les débuts de la mécanique
On doit ces principes à Galilée et Huygens, mais ils ont été affinés par la suite par Clairaut, Descartes, Euler et D'Alembert.
Galilée (1564-1642) était d'abord un physicien et il étudia la mécanique et la dynamique des corps en mouvement. Il démontra l'invariance de l'accélération dans le champ de pesanteur terrestre à la surface du globe et établit la loi de l'inertie (tout corps non soumis à une force extérieure est animé d'un mouvement rectiligne uniforme et se trouve dans un référentiel que l'on nomme aujourd'hui "galiléen").
Christian Huygens (1629-1695), hollandais, développa une théorie ondulatoire de la lumière. En 1673, il publia la loi sur l'accélération centrifuge des corps en mouvement circulaire. Il séjourna quinze ans en France sur l'invitation de Colbert.
René Descartes (1596-1650) apporta alors une vision complètement nouvelle de l'univers. L'univers évolue seul : il n'est point besoin d'un dieu intervenant à tout moment. Descartes étudia l'optique et fit une théorie de la réflexion et de la réfraction. Il introduisit les concepts mathématiques en physique, en particulier un système de coordonnées aujourd'hui dites cartésiennes facilitant les calculs.
Alexis Clairaut (1713-1765) fut l'un des membres de l'expédition en Laponie. Il s'attaqua à des problèmes de mécanique céleste comme celui des 3 corps appliqué au système Terre-Lune perturbé par le Soleil. Il appliqua la théorie de la gravitation universelle aux comètes, en particulier aux perturbations de Jupiter et Saturne sur la trajectoire de la comète de Halley.
Leonhard Euler (1707-1783), mathématicien suisse, étudia les perturbations mutuelles de Jupiter et de Saturne ainsi que les orbites paraboliques des comètes. On lui doit la définition des "angles d'Euler" permettant la détermination de la position d'un solide en mouvement dans un trièdre trirectangle.
Jean-Baptiste Le Rond d'Alembert (1717-1783) publia un traité de dynamique contenant le théorème sur les forces d'inertie connu aujourd'hui sous le nom de théorème de d'Alembert. Il établit également les équations du mouvement de la Terre autour de son axe et réalisa la première théorie mathématique de la précession.
La gravitation universelle
Le caractère universel de la gravitation a été mis en évidence par Newton (1642-1727) dans son œuvre "Principes mathématiques de philosophie naturelle". Newton a été le premier à comprendre que la pomme qui tombe d'un arbre et la Lune qui tourne autour de la Terre obéissent à une même loi et que leurs mouvements sont en fait de même nature.
La loi de la gravitation universelle s'énonce ainsi : "deux points matériels de masse m et m' exercent l'un sur l'autre une force attractive directement proportionnelle aux masses et inversement proportionnelle au carré de la distance r les séparant". Le module F de cette force vaut :
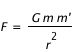 où G est la constante gravitationnelle.
où G est la constante gravitationnelle.
Cette loi suppose la transmission instantanée des forces dans l'espace.

Portrait de Sir Isaac Newton
Crédit :
Danielle Briot - Collection particulière
La mécanique céleste
La mécanique céleste est alors l'application de la mécanique newtonienne et des principes fondamentaux de la mécanique aux corps du système solaire. C'est Laplace qui a mis en place les fondements de la mécanique céleste qui va (presque) tout expliquer :
- le mouvement des planètes et de leurs satellites
- la précession et la nutation
- les marées
- l'applatissement des planètes
En première approximation, la mécanique newtonienne explique donc parfaitement les mouvements dans le système solaire. Mais avant d'aborder un cas aussi complexe, on s'intéresse d'abord au problème restreint à 2 corps.

Pierre Simon de Laplace
Crédit :
Danielle Briot - Collection particulière
Dynamique du système solaire
Le problème à deux corps
Le problème à 2 corps s'intéresse à 2 solides, assimilés à leur centre de masse, seuls à interagir. Ce problème est soluble analytiquement, relativement simplement, en travaillant dans le référentiel du centre de masse du système ; le reste de l'Univers étant oublié, le centre de masse est isolé et fournit un bon référentiel galiléen pour l'étude du mouvement.
- Tout d'abord, on peut montrer que le mouvement des 2 corps l'un autour de l'autre est plan. Ceci résulte du fait que le moment cinétique du système est constant, car l'interaction est centrale, toujours dirigée vers le barycentre du système.
- Ensuite, l'interaction gravitationnelle se traduisant par un "champ de force", il en découle que l'énergie du système est également constante.
- Enfin, le module de la force évoluant comme l'inverse du carré de la distance entre les 2 corps, un autre invariant apparaît. Cet invariant se traduit par le vecteur excentricité, et la trajectoire relative d'un corps par rapport à l'autre s'apparente à un cercle, une ellipse, une parabole ou une hyperbole. Cette trajectoire, dans le plan du mouvement, est définie par son demi-grand axe, de mesure a, et l'excentricité e.
C'est dans le cadre de plusieurs problèmes à deux corps (pour chaque couple planète-Soleil) que s'appliquent les lois de Kepler.
Les mouvements dans le système solaire
Dans le système solaire on trouve plus de deux corps et pour obtenir les mouvements des planètes avec une très bonne précision, il faut envisager un problème de N corps s'attirant mutuellement.
Le principe du problème des N corps de masse m
i
Chacun des N corps de masse m
i exerce sur le corps repéré par j une force proportionnelle au produit de leurs masses, et inversement proportionnelle au carré de leur distance. Cette force s'écrit :
![F_j = \[\sum_{i=1 (i\neq j)}^N\]\frac{k~m_i~m_j~P_i~P_j}{\mid P_i~P_j\mid ^3}](../pages_mecanique-celeste/equations_dynamique-systeme/equation1.png)
Crédit : CNRS/Jean-Eudes Arlot
Mais si on regarde d'un peu plus près, on se rend compte qu'on est en présence d'un très gros corps, le Soleil, mille fois plus massif que la plus grosse des planètes, Jupiter, entouré de petits corps tournant autour de lui. Chaque couple Soleil-planète est un problème à deux corps. On peut considérer en première approximation la masse m de la planète comme négligeable devant celle du Soleil (notée M) et la force subie par la planète est alors :
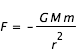
Le coefficient GM, produit de la constante gravitationnelle et de la masse du Soleil, est alors le même pour toutes les planètes, ce que Kepler (1571-1630) avait remarqué sans le démontrer.
Dans le cas de N corps, on considérera que l'on a toujours des mouvements de deux corps deux à deux avec une perturbation par les autres corps entraînant une variation des paramètres de l'orbite elliptique du petit corps tournant autour du plus gros. C'est Lagrange (1736-1813) qui introduisit les équations décrivant ces mouvements perturbés.
La vitesse de libération
Lorsque l'on veut quitter un corps céleste -la Terre par exemple- et échapper à son attraction, il faut vaincre les forces de gravitation et surtout éviter de retomber sur le sol. Deux cas se présentent :
- éviter de retomber sur le sol mais rester en orbite autour de la Terre : trajectoire fermée (cercle ou ellipse)
- quitter l'attraction terrestre en s'éloignant indéfiniment (trajectoire hyperbolique)
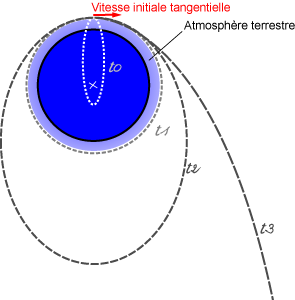
Crédit : CNRS / Jean-Eudes Arlot et ASM / Gilles Bessou
En première approximation, la trajectoire d'une pierre lancée depuis le sol est une parabole si on suppose la Terre plate et le centre d'attraction à l'infini. En réalité, la trajectoire est une ellipse dont le centre de la Terre est le foyer. Il faut circulariser l'orbite pour éviter que la trajectoire heurte la surface terrestre. Notons que l'altitude minimum pour satelliser un objet est de 300 km pour éviter le freinage par l'atmosphère terrestre.
- v > 8 km/s : la trajectoire est circulaire et ne heurte plus la Terre (trajectoire T1)
- v < 8 km/s : la vitesse est insuffisante et l'objet retombe sur Terre (trajectoire T0)
- 8 km/s < v < 13 km/s : la trajectoire est une ellipse dont le périgée correspond au point de lancement (trajectoire T2 fermée)
- v > 13 km/s : la trajectoire n'est plus fermée ; le mobile va s'éloigner à l'infini sur une trajectoire hyperbolique
Les points de Lagrange
Sur l'orbite décrite par un corps autour d'une masse centrale, on va trouver des points d'équilibre utiles pour les satellites artificiels d'observation : les points de Lagrange.
Pour obtenir une modélisation des mouvements dans le système solaire, on va partir du problème simplifié dans lequel les trajectoires des planètes sont des ellipses mais les éléments de ces ellipses vont varier au cours du temps. Cette ellipse de base est appelée ellipse osculatrice. Pour chaque planète on va considérer un problème à deux corps perturbé par les autres planètes. C'est Lagrange (1736-1813) au XVIIIème siècle qui a posé les équations du problème. Lagrange a aussi noté que dans un système à deux corps, il existait des positions d'équilibre où des corps supplémentaires pouvaient rester captifs. Ces positions sont appelées aujourd'hui les points de Lagrange du système à deux corps. La figure ci-dessous montrent l'emplacement des 5 points L1, L2, L3, L4, L5. Seuls les points L4 et L5 sont des points d'équilibre stables. Des astéroïdes sont piégés sur ces points de l'orbite de Jupiter et de celle de Mars. Les points L1 et L2 de la Terre permettent d'installer des télescopes d'observation (SOHO, un satellite d'observation du Soleil en L1 et bientôt GAIA, un satellite d'observation astrométrique de la galaxie en projet en L2). Les points L1 et L2 sont à 1,5 millions de kilomètres de la Terre.
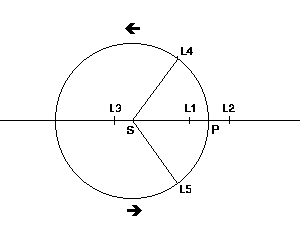
Les points de Lagrange L1, L2, L3, L4 et L5 par rapport à l'orbite
d'une planète P autour du Soleil S. Seuls L4 et L5 sont stables.
Les angles (SP, SL4) et (SP, SL5) font chacun 60°.
Crédit : CNRS / Jean-Eudes Arlot
Les satellites géostationnaires
Un satellite géostationnaire est vu immobile depuis la surface de la Terre : pourquoi ? Non pas parce qu'il est réellement immobile par rapport à la Terre, mais parce qu'il tourne à la même vitesse que la Terre autour de son axe. Il doit faire une révolution en 24 heures ! (en fait en 23 heures 56 minutes 4 secondes qui est la période de rotation sidérale autour de la Terre).
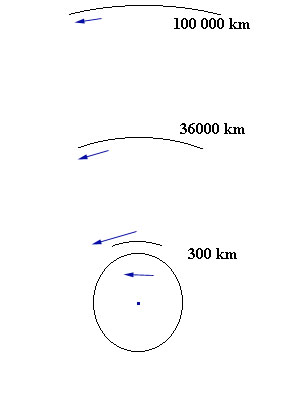
Période de révolution selon l'altitude
Altitude 100 000 km : 3,5 jours
Altitude 36 000 km : 24 heures
Altitude 300 km : 1 heure et demie
Crédit : CNRS / Jean-Eudes Arlot
En savoir plus: calcul des périodes des satellites artificiels de la Terre
 En savoir plus
En savoir plus
Un satellite artificiel de la Terre tourne d'autant moins vite qu'il est loin de la Terre pour respecter la 3ème loi de Kepler qui dit que a3/T2 est une constante pour les objets tournant autour d'un même corps, où a est le demi-grand axe de l'orbite et T la période de révolution.
Cette constante est, pour la Terre : GM/4π2 où G est la constante de la gravitation et M la masse de la Terre soit :
G=6,67259x10-11 m3kg-1s-2 et M=5,9736x1024 kg et donc GM/4π2 = 1,00965x1013
En supposant les orbites circulaires, un satellite situé à 300 km d'altitude (orbite basse) aura une période de révolution de T :
a = 300 km + 6378 km = 6,678x106 m ; donc a3 = 297,81x1018 m3
Appliquons la formule a3/T2 = GM/4π2 = 1,00965.1013
donc T2 = a3/1,00965x1013 = 297,81x1018/1,00965x1013 = 29496358 secondes, soit T = 5431,055 secondes, c'est-à-dire, environ une heure et demie.
Calculons la distance a au centre de la Terre à laquelle doit se trouver un satellite artificiel pour être géostationnaire.
T doit être égal à 23 heures 56 minutes 4 secondes, soit 86164 secondes ; on a T2 = 7424234896 s2 donc a3 = T2x1,00965x1013 = 74,95878763x1021 (voir ci-dessus) et ainsi a = 4,21639 x 107 mètres soit 42 163 km. En retranchant le rayon terrestre, on obtient l'altitude d'un satellite géostationnaire : environ 36 000 kilomètres.
On peut faire le même calcul avec des satellites plus éloignés et on verra que la durée de révolution augmente et atteint 28 jours pour un corps situé à 300 000 kilomètres de la Terre : c'est la Lune !
Les transferts d'orbites par impulsion gravitationnelle
Les sondes spatiales utilisent le "rebond" gravitationnel pour aller plus loin et plus vite, en économisant du carburant, nécessaire pour échapper à l'attraction terrestre. On utilise pour cela les lois de Kepler et le mouvement des deux corps : la sonde va suivre un mouvement képlérien par rapport à un corps central A, la Terre, par exemple. Le corps A est prépondérant et on va mettre la sonde sur une orbite elliptique dont l'apogée est proche d'un autre corps que l'on va utiliser. A l'apogée (point de l'orbite le plus éloigné du corps A), la présence prépondérante du corps B va modifier la trajectoire de la sonde. Des petites manoeuvres vont permettre de mettre la sonde sur une nouvelle orbite elliptique centrée sur le corps B pour lui permettre d'avoir une nouvelle trajectoire.
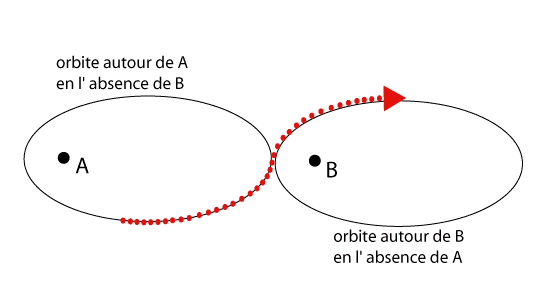
Ce principe est couramment utilisé par les sondes qui doivent se diriger vers l'extérieur du système solaire (planètes Jupiter, Saturne, Uranus et Neptune).
Crédit : CNRS / Jean-Eudes Arlot
Les satellites gardiens des anneaux

Crédit : NASA/C. J. HAMILTON
Les planètes géantes présentent la particularité d'être entourées d'anneaux. Saturne possède le plus spectaculaire. La formation d'un anneau est le résultat des collisions entre une mutlitude de petits cailloux en orbite autour de la planète. Ces petites particules de roche et de glace étant en rotation autour de la planète, elles s'organisent sous forme d'un disque plat.
Les divisions - espaces vides - qui apparaissent à l'intérieur d'un même anneau, sont longtemps restées inexpliquées. C'est la découverte de petits satellites orbitant dans ces espaces vides qui nous ont fournis l'explication.
Ci-contre, on a représenté un satellite orbitant dans une des divisions d'un anneau.
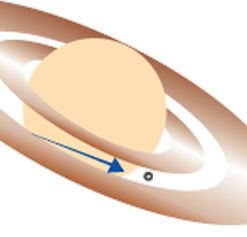
Premier temps : une particule se détache de l'anneau et pénètre dans la division ; elle s'approche du satellite.
Crédit : ASM

Deuxième temps : le satellite va modifier la trajectoire de la particule (mouvement des deux corps) et augmenter l'excentricité de sa trajectoire. Elle retournera donc dans l'anneau.
Crédit : ASM
Troisième temps : de retour dans l'anneau, la particule subira de nouveau des collisions qui vont circulariser son orbite et lui éviter de retourner dans la division.
Crédit : ASM
Ainsi, on a l'impression que le satellite repousse les cailloux hors de la division. Il n'y a pas d'effet de répulsion : tout est conforme aux lois de la gravitation universelle.
QCM
Les théories du mouvement des planètes
Remarques générales sur les théories planétaires
Le mouvement des planètes autour du Soleil est un cas particulier du problème des N corps pour lequel on n'a pas de solution exacte pour N supérieur à 2. Tous les corps s'attirent les uns les autres conformément à la loi de la gravitation mais on considère que les planètes ont une masse faible devant celle du corps central, le Soleil. On recherche des solutions approchées du problème fondées sur la théorie des perturbations, où les coordonnées sont des fonctions du temps t, des masses des corps en présence et des constantes d'intégration. On obtient ces solutions en construisant des théories analytiques ou en effectuant des intégrations numériques.
En savoir plus: théories analytiques ou intégration numérique ?
 En savoir plus
En savoir plus
Dans les théories analytiques, les coordonnées sont obtenues sous forme de combinaisons de fonctions algébriques et trigonométriques analytiques du temps t et des paramètres du problème, masses et constantes d'intégration. Calculer une position avec de telles théories est long mais relativement simple puisqu'il suffit de substituer le paramètre "temps" dans les séries. Jusqu'à l'apparition des ordinateurs, il était nécessaire de construire des tables intermédiaires à partir desquelles on pouvait fabriquer des éphémérides.
Les intégrations numériques donnent les valeurs numériques des coordonnées et des vitesses pour des valeurs t0, t0+h, t0+2h, etc., t0 étant le temps initial et h étant le pas d'intégration. Les méthodes d'intégration numérique sont bien adaptées aux calculs par ordinateur et elles ont été particulièrement utilisées aux Etats-Unis. Cependant, pour calculer une position, il est indispensable de construire des tables intermédiaires à l'aide de l'intégration numérique. Ces tables seront utilisées pour la fabrication des éphémérides.
En savoir plus: La découverte de Neptune par Le Verrier
 En savoir plus
En savoir plus
La mécanique céleste allait prouver sa force en permettant de découvrir une nouvelle planète dans le système solaire, par le calcul et non pas seulement par l'observation du ciel.
Le Verrier avait établi un modèle de mouvement d'Uranus à partir des lois de la dynamique et de la gravitation universelle. Mais la comparaison aux observations ne donnait pas satisfaction : Uranus se trouvait trop loin, par rapport à son orbite calculée. La différence ne pouvait pas être expliquée par l'imprécision des observations: elle était bien plus grande. Le Verrier supposa qu'un corps massif attirait Uranus hors de son orbite. Mais où pouvait bien se trouver ce corps ? Quel était-il ? L'étude des observations d'Uranus réalisées entre 1800 et 1850 permit d'en calculer la masse et la distance. L'orbite ainsi calculée montrait qu'il s'agissait d'une nouvelle planète, au-delà d'Uranus. Le même calcul fut fait par Adams en Angleterre mais c'est Le Verrier qui fit observer par Galle à Berlin en 1846 la nouvelle planète. En fait, l'orbite de Neptune était un peu différente de celle calculée, mais les observations d'Uranus disponibles ne permettaient pas une meilleure précision.
La découverte de Pluton au XXème siècle ne s'est pas faite ainsi, la masse de Pluton étant trop faible pour perturber neptune.
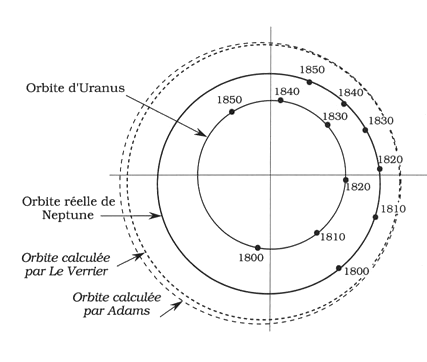
Orbite théorique et orbite observée avant la découverte de Neptune
Crédit : CNRS
L'argument temps dans les théories planétaires
Il convient de dire maintenant quelques mots sur l'argument "temps" des éphémérides. En effet, pour connaître une position à un instant donné, quel instant chercher dans les éphémérides ? Jusqu'en 1834, on a utilisé le temps solaire vrai de Paris. Ensuite, du fait de l'existence d'horloges plus fiables, on a utilisé le temps moyen de Paris. En 1916, suite à une convention internationale, on a utilisé le temps moyen de Greenwich. Ces temps étaient jusque là liés à la rotation de la Terre considérée comme suffisamment uniforme. La mise en évidence d'irrégularités dans cette rotation (ralentissement) amena les astronomes à introduire une échelle de temps uniforme pour le calcul des éphémérides, échelle de temps basée sur la révolution de la Terre autour du Soleil. On utilisa le Temps des éphémérides défini à partir de la théorie du Soleil de Newcomb, ou encore, comme dans la Connaissance des temps, le Temps uniforme de Le Verrier tiré de sa théorie du Soleil et donc très proche du précédent. A partir de 1984 on introduisit le Temps terrestre, temps uniforme construit à partir des horloges atomiques beaucoup plus stables que les mouvements célestes pour construire une échelle de temps.
Ainsi, si on utilise le Temps Universel comme argument des éphémérides, on verra les planètes accélérer... C'est en fait la Terre qui ralentit...
Application : l'évolution de l'excentricité de l'orbite terrestre
La mécanique céleste permet également d'obtenir, à une précision plus faible que celle des éphémérides valables sur quelques siècles, l'évolution des orbites planétaires sur de très longues durées de l'ordre de plusieurs millions d'années. On constate ainsi que l'excentricité de l'orbite terrestre subit de larges variations formées de nombreux termes périodiques dont les plus importants ont des périodes voisines de 100 000 ans, et pour l'un d'eux, une période de 400 000 ans. Les travaux de l'Institut de mécanique céleste, depuis les années 1970, ont permis de confirmer définitivement l'hypothèse astronomique des variations climatiques de la Terre au cours de l'ère quaternaire. Les paléoclimatologues montrent en effet la corrélation entre les variations des éléments de l'orbite terrestre et les grandes glaciations du quaternaire. L'orbite circulaire de la Terre correspond à une glaciation et une orbite elliptique à une période chaude. La grande précision de la mécanique céleste offre ainsi une horloge à la paléoclimatologie en lui donnant les dates des glaciations et des périodes interglaciaires.
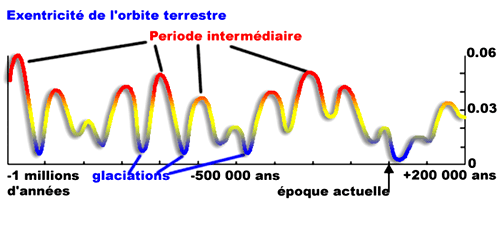
Variations de l'excentricité de l'orbite terrestre sur 1 200 000 ans.
Dans 27 000 ans l'excentricité sera presque nulle, l'orbite de la Terre presque circulaire ce qui entraînera une glaciation si, d'ici là, l'atmosphère de la Terre
n'est pas profondément modifiée.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
QCM
La gravitation universelle et la relativité
Auteur: Jean-Eudes Arlot
Introduction
 Introduction
Introduction
La gravitation universelle a expliqué beaucoup de choses mais reste en elle-même inexpliquée. Une nouvelle approche de la description de l'univers va permettre d'expliquer certaines choses que la gravitation universelle de Newton n'expliquait pas.
La gravitation newtonnienne
Les limites de la gravitation universelle
Rappelons la loi de Newton : F = -Gmm'/r2 où F est la force exercée l'un sur l'autre par deux corps de masses respectives m et m' séparés d'une distance r. G est appelée constante de la gravitation.
D'autre part, le principe d'inertie découvert par Galilée stipule qu'un corps qui se déplace sans interaction avec l'extérieur, continuera sur une trajectoire rectiligne indéfiniment. Newton ajoutera que le seul moyen de modifier cette trajectoire est d'utiliser une force : un objet subissant une force accélère d'une quantité inversement proportionnelle à la masse de l'objet dans la direction de la force.
Tous ces principes vont nous permettre de décrire les mouvements dans le système solaire mais, avouons-le, ils n'expliquent pas grand-chose. On est en présence d'une action à distance. Pourquoi les corps s'attirent-ils ? Nul ne le sait. Avant Newton, on pensait que des anges poussaient les planètes sur leurs orbites ; après Newton, on sait que les anges ne poussent pas les planètes mais les tirent vers le corps central pour contrecarrer le principe d'inertie ! Aucun mécanisme n'a été mis en évidence pour expliquer l'action de cette force.
La théorie de Newton explique aussi l'aplatissement du globe terrestre et permet de décrire correctement les marées. On avait bien pensé auparavant que la Lune pouvait attirer l'eau des mers mais alors la marée aurait dû n'être haute que du côté de la Lune. Newton l'explique : la Terre tourne autour du Soleil, elle n'est pas dans un repère galiléen et subit l'attraction de la Lune. Rien ne maintient la Terre pendant que l'eau monte vers la Lune. Le différentiel des forces explique bien les marées hautes de part et d'autre de la Terre. Enfin la gravitation universelle ne s'applique pas qu'au système solaire mais à l'univers tout entier.
Elle n'explique pas l'excès d'avance du périhélie de Mercure.
Pour expliquer ce dernier point, il est nécessaire de faire appel à la théorie de la relativité générale pour laquelle :
- il n'y a pas de temps absolu
- la notion de référentiel galiléen n'est plus pertinente
- il n'y a plus de forces à distance mais un champ de gravité se propageant à la vitesse de la lumière.
En savoir plus: l'excès d'avance du périhélie de Mercure
 En savoir plus
En savoir plus
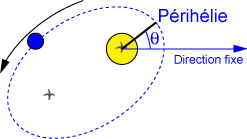
Périhélie : point où Mercure est au plus près du Soleil. l'angle θ est l'angle entre une direction fixe et la direction du périhélie.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
Le système Soleil Mercure n'est pas isolé dans l'espace et subit des perturbations gravitationnelles qui peuvent faire varier l'angle θ qui donne la position du périhélie de Mercure. Ainsi θ va varier et le périhélie va sembler "avancer" au cours du temps. la mécanique newtonnienne permet de calculer cette avance mais les observations ont montré que le périhélie avance plus rapidement que prévu. Le Verrier a cherché une planète inconnue dont les perturbations expliqueraient cet excès d'avance mais ne l'a pas trouvé. Il faudra attendre Einstein et la théorie de la relativité générale pour l'expliquer.
La constante de la gravitation
Dans la formule de Newton ci-dessus, on remarque l'existence d'une constante G. A quoi correspond-elle ? Quelle est sa valeur ? En fait, la mesure des distances et des périodes dans le système solaire ne nous fournit que le produit Gm de la constante G avec la masse du corps central. On connaît donc G x (masse solaire) en mesurant les positions des planètes, G x (masse terrestre) en mesurant le mouvement de la Lune, G x (masse de Jupiter) en mesurant les positions des satellites de Jupiter, etc. La mesure absolue de G a été faite par Cavendish (1731-1810) en 1798. Pour cela il réalise une expérience désormais célèbre : il mesure l'attraction de deux boules de plomb de 150 kg chacune sur de petites billes par l'intermédiaire d'un pendule de torsion. Il pourra dire : j'ai pesé la Terre ! La valeur de cette constante est 6,672 59 x 10-11 m3 kg-1 s-2.
Une question se pose aussi : la constante de la gravitation est-elle vraiment constante ou se modifie-t-elle au cours du temps ? Il a été impossible de mesurer une variation de cette constante mais cette variation, si elle existe, ne peut être que faible. En effet, en supposant que cette constante ait varié de 10% au cours du dernier milliard d'années, les conditions de rayonnement du Soleil auraient été telles que la vie aurait été impossible sur Terre à cette époque. La variation de cette constante ne peut donc être que beaucoup plus faible que cela.
Exercice
 La constante de gravitation
La constante de gravitation
Question 1)
Cette détermination nous permet de connaître la masse des corps du système solaire et de résoudre des problèmes tels que :
quelle serait la durée de révolution d'une bille de masse négligeable autour d'une masse d'un kilogramme situé à un mètre dans l'espace ?
Les principes de la relativité
Après avoir vu la gravitation universelle au sens de Newton, venons-en au principe de relativité. Ce principe n'est pas récent. Dès les prémices de la mécanique, la question qui s'est posée est : les lois de la physique que l'on met à jour restent-elles invariantes dans n'importe quel référentiel ? Y-a-t-il un référentiel absolu ? C'est à cette question fondamentale que les théories de la relativité vont tenter de répondre.
En 1905, A. Einstein (1879-1955) publie sa théorie de la relativité restreinte et, en 1916, celle de la relativité générale.
La relativité galiléenne
Avant même la découverte de la gravitation universelle par Newton, Galilée énonce le principe de l'inertie : tout corps abandonné à lui-même et ne subissant aucune force extérieure, est animé d'un mouvement rectiligne uniforme. On appellera "référentiels galiléens" des systèmes de référence en mouvement de translation rectiligne uniforme les uns par rapport aux autres. Pour passer d'un référentiel R à un référentiel R' animé d'une vitesse v parallèle à l'axe des abscisses, le changement de variable est de la forme :
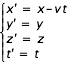
Dans cette transformation dite "galiléenne", les lois de la mécanique et de la physique sont supposées être invariantes. Les vitesses s'additionnent. Afin de respecter le principe d'inertie, Newton sera amené à introduire un temps absolu et un espace absolu universel.
Les limites de la relativité galiléenne
Ce système simple va vivre pendant plus d'un siècle et la mécanique céleste va décrire merveilleusement la dynamique du système solaire jusqu'à ce que deux grains de sable se glissent dans la machine. L'un sera l'inexplicable excès de l'avance du périhélie de Mercure. La mécanique classique sera impuissante devant ce problème. L'autre viendra de la découverte de l'électromagnétisme. En 1873, J. Maxwell (1831-1879), physicien écossais, publie les équations générales des champs électromagnétiques, dites "équations de Maxwell". On constate alors que ces équations ne sont pas invariantes. Effectivement, la composition des vitesses ne fonctionnent pas avec la vitesse de la lumière qui ne dépend pas de la vitesse de la source (cela se remarquerait lors de l'observation des étoiles doubles) et ne peut être composée avec une autre vitesse. Serait-ce dû à l'existence d'un "éther" dans lequel la lumière se déplace par vibration ? On chercha alors à déceler un mouvement par rapport à l'éther. En particulier, on devait pouvoir mesurer la vitesse d'un mobile en mesurant les modifications des lois physiques entraînées par le déplacement. Ce fut alors la célèbre expérience de Michelson qui consiste à mesurer la vitesse de la lumière dans deux directions perpendiculaires. Cette expérience fut faite en divers lieux, à 6 mois d'intervalle (la vitesse de la Terre change de sens) pendant des dizaines d'années et jamais on ne trouva un changement dans la vitesse de la lumière. Le mouvement de la Terre était indétectable avec cette méthode. Les équations de Maxwell étaient-elles fausses ? En fait non, c'était la transformation galiléenne qui n'était pas correcte. H. Poincaré montra que les équations de Maxwell étaient invariantes si on leur appliquait une transformation particulière, dite "transformation de Lorentz".
La relativité d'Einstein
La relativité restreinte
Einstein va réussir à étendre le principe de relativité de la mécanique à la physique à partir de deux postulats :
- tous les référentiels galiléens sont équivalents pour la formulation des lois physiques ;
- la vitesse de la lumière dans le vide est constante par rapport à n'importe quel système galiléen et est indépendante du mouvement de la source.
Ces deux postulats étaient bien sûr incompatibles avec la transformation galiléenne qui postule qu'il existe un temps absolu et que la mesure d'une longueur est indépendante du mouvement du système de référence. Einstein va montrer les erreurs de ces postulats. En particulier, il montre la relativité de la notion de simultanéité qui n'a de signification que dans un système galiléen déterminé, ce qui entraîne la relativité de la notion de longueur. Longueur et temps sont liés. La transformation galiléenne doit, comme prévu, être remplacée par la transformation de Lorentz :
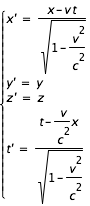
pour deux repères ayant leurs axes parallèles et en déplacement relatif selon l'axe x.
La loi de composition des vitesses n'est plus celle du système galiléen.
Cette transformation va entraîner la contraction des longueurs et la dilatation des durées pour les corps en mouvement. On remarquera que pour des vitesses relatives petites devant c (i.e. v/c petit), la transformation de Lorentz se réduit à la transformation de Galilée.
En savoir plus: la dynamique relativiste
 En savoir plus
En savoir plus
Les lois de la dynamique newtonnienne sont aussi à modifier : elles doivent être invariantes dans une transformation de Lorentz.
La quantité de mouvement p = mv devient :
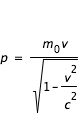
Dans la mécanique newtonnienne, la notion de masse a deux sens : sa détection par son poids (masse gravifique) et sa détection par sa résistance au mouvement (masse inerte). Ces masses sont proportionnelles et on choisit les unités de façon à ce qu'elles soient identiques. En identifiant l'expression ci-dessus avec p=m(v).v, on en déduit que :
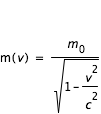
où m0 est la masse au repos.
La relativité d'Einstein introduit donc la notion de masse au repos et induit une augmentation de la masse avec la vitesse.
Quant à la loi de conservation de l'énergie, elle devient :
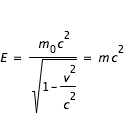
soit en développant :
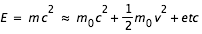
La théorie d'Einstein introduit un terme nouveau : 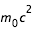
qui correspond à l' "énergie interne" en plus de l'énergie cinétique et il y a ainsi équivalence entre masse et énergie.
Tous ces faits nouveaux ont été vérifiés par la physique des particules qui permet d'obtenir de très grandes vitesses. Aux basses vitesses, on retrouve les lois de la dynamique newtonnienne.
La relativité générale
La relativité restreinte n'a cependant pas résolu tous les problèmes. Elle s'est montrée incapable d'incorporer la gravitation de manière satisfaisante et certaines expériences semblent toujours prouver qu'il existe un référentiel absolu. Par exemple, l'expérience du pendule de Foucault semble indiquer que l'on peut mesurer le mouvement de la Terre par rapport à un référentiel absolu. Où donc se trouve la contradiction ? Einstein va étendre pour cela la relativité restreinte à la gravitation. Pour cela Einstein va énoncer le principe d'équivalence. L'identité entre la masse gravifique et la masse inertielle devient un postulat de base de la théorie. Ainsi, il n'est pas possible, localement, de distinguer une force créée par une accélération d'une force créée par la gravitation. Cette identité a conduit Einstein à penser qu'un laboratoire en chute libre dans un champ gravitationnel constitue en quelque sorte l'extension naturelle du concept de système de référence inertiel de l'ancienne mécanique. On est ainsi amené à postuler que "tous les systèmes de référence en chute libre sont équivalents pour l'expression des lois physiques non gravitationnelles, quel que soit leur état de mouvement et leur localisation". Cet énoncé constitue ce qu'on appelle aujourd'hui le principe d'équivalence d'Einstein.
Il faut souligner à ce propos que ce principe n'édicte rien sur la description des phénomènes gravitationnels eux-mêmes. Ainsi, il ne postule pas que deux laboratoires en chute libre situés en des endroits différents vont trouver la même valeur pour la constante de la gravitation G (étant admis qu'ils sont munis d'horloges et de mètres de même fabrication). Autrement dit, le principe d'équivalence d'Einstein ne rejette pas a priori que la "vraie théorie relativiste de la gravitation" puisse prédire que G varie avec le temps et le lieu. Ce principe permet donc des généralisations de la relativité générale, généralisations dont les vérifications font l'objet de nombreuses recherches actuelles.
L'idée qu'en présence d'un champ gravitationnel, ce sont les référentiels en chute libre qui doivent remplacer les référentiels inertiels en amène très naturellement une autre : les référentiels en chute libre ne peuvent être que locaux, car un vrai champ de gravitation (celui de la Terre par exemple) n'est pas uniforme. En effet, la non uniformité entraîne qu'aucun mouvement global du système de référence ne peut supprimer partout le champ de la Terre. D'où l'idée que le principe d'équivalence d'Einstein, qui est purement local, n'interdit pas à la géométrie de l'espace-temps de changer d'un point à un autre. Au contraire, un tel changement de géométrie permet de résoudre le problème de la gravitation avec une extrême élégance conceptuelle. Le principe d'inertie galiléen nous dit qu'en l'absence de tout champ de force, un point matériel a un mouvement rectiligne uniforme dans tout référentiel galiléen. Or, une droite est une géodésique de l'espace euclidien. Il est dès lors naturel de considérer le mouvement d'une particule en chute libre dans un champ gravitationnel comme défini par une géodésique d'une métrique plus complexe qu'une métrique euclidienne. En fait, Einstein a introduit une généralisation dite "pseudo-riemanienne" de la métrique spatio-temporelle de la relativité restreinte.
Nous donnons ci-dessous une analogie qui permet de comprendre pourquoi une métrique non euclidienne peut rendre compte de façon simple d'une force de gravitation.
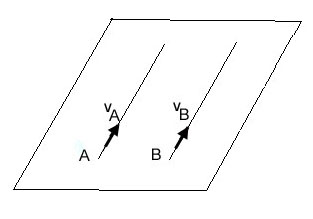
Plan euclidien P : deux corps A et B initialement doués de vitesse vA = vB et suivant des géodésiques de P (droites) vont rester à distance constante : il n'y a pas de gravitation dans cet univers : A et B ne "s'attirent" pas.
Crédit : CNRS/Jean-Eudes Arlot
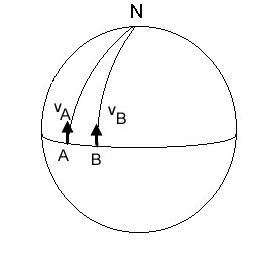
Sphère S : deux corps A et B initialement doués de vitesse vA = vB sur l'équateur et suivant des géodésiques de S (grands cercles) vont se rapprocher et se rejoindre au pôle N : il y a de la gravitation dans cet univers : A et B "s'attirent".
On peut donc décrire la gravitation comme une manifestation de la courbure d'une métrique.
Crédit : CNRS/Jean-Eudes Arlot
Les preuves expérimentales de la relativité générale
La théorie de la relativité générale a permis d'expliquer plusieurs phénomènes importants :
- l'excès d'avance du périhélie de Mercure se trouve parfaitement modélisé dans le cadre de la relativité générale ;
- la courbure des rayons lumineux passant près d'une masse est détectée en observant les étoiles proches du Soleil pendant une éclipse ;
- les mirages gravitationnels (effet de lentille d'une masse importante se trouvant sur le trajet de rayons lumineux) ont été observés (cf. ci-dessous) ;
- l'expansion de l'univers découverte par Hubble grâce au décalage spectral vers le rouge des galaxies.

Cette image du télescope spatial HST de l'amas de galaxies Abell 2218 montre un exemple spectaculaire de lentille gravitationnelle. Les arcs visibles sur l'image sont des mirages créés par le champ gravitationnel de l'amas. L'amas est tellement massif et compact que les rayons lumineux passant à travers cet amas sont déviés et, comme à travers une lentille, forment une nouvelle image. Ce processus déforme l'image primaire des objets se trouvant beaucoup plus loin que l'amas de galaxies provoquant le phénomène.
Crédit : NASA/STSCI
QCM
La mesure du temps
Auteur: Jean-Eudes Arlot
Introduction
 Introduction
Introduction
Nos méthodes de mesure du temps reposent sur ce que l'on a d'abord cru parfait et immuable : le mouvement de la Terre. Très tôt, les civilisations ont eu besoin de mesurer le temps qui s'écoule : les êtres humains ont besoin de repères communs temporels pour se rencontrer. Il est donc nécessaire de mesurer les durées par rapport à un étalon de base et de dater les événements se produisant au cours de l'écoulement du temps. L'utilisation des mouvements célestes comme horloge a été l'idée la plus naturelle, ces mouvements paraissant de prime abord immuables, réguliers et uniformes. L'augmentation de la précision de mesure du temps va montrer qu'il n'en est rien et la recherche d'un temps vraiment uniforme va rendre obsolètes les vieilles définitions. Notre rythme de vie lié aux jours et aux saisons va nous faire conserver nos unités et échelles de temps anciennes.
Le temps astronomique
Les mouvements de la Terre
Les mouvements de la Terre autour de son axe ou autour du Soleil semblent immuables, réguliers, uniformes et paraissent parfaits pour concrétiser une échelle de temps qui doit être, elle-aussi, immuable, régulière et uniforme. Ainsi, la rotation de la Terre autour de son axe définit le jour et la révolution de la Terre autour du Soleil définit l'année.
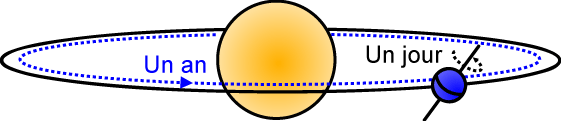
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
Pour définir parfaitement le mouvement de la Terre, il faut connaître :
- le mouvement de l'axe de la Terre par rapport à l'"extérieur" (c'est-à-dire par rapport à un référentiel inertiel) ; c'est ce mouvement qui définit le mouvement de l'équateur céleste et la modification des coordonnées (précession et nutation) ;
- le mouvement de l'axe de rotation de la Terre par rapport à la Terre elle-même : il est très petit puisque le pôle reste dans un cercle d'une vingtaine de mètres mais ce mouvement est imprévisible ;
- le mouvement de la Terre autour de son axe de rotation : c'est évidemment le plus important qui va définir la notion de jour. Il s'exprime par la variation d'un angle, le temps sidéral, et on verra qu'il n'est pas uniforme : la Terre ralentit, mais avant de s'en apercevoir, il va falloir résoudre d'autres problèmes.
Définition du jour
Si on considère une direction fixe dans l'espace, il faudra 23h 56m 4s à un observateur pour se retrouver dans la même direction après un tour complet de la Terre autour de son axe. Mais ce n'est pas cette durée qui est la plus facile à percevoir. On aura beaucoup plus l'impression que la Terre a accompli un tour si c'est le Soleil qui revient à la même position. C'est ce retour du Soleil dans la même direction qui définit le jour qui lui, dure en moyenne, 24 heures. En effet, la Terre s'est déplacée et le Soleil ne correspond pas à une direction fixe.
Le jour n'est pas, a priori, une simple unité de temps pour compter des durées, mais c'est plutôt un intervalle de temps centré sur une période de "jour" et encadré par des périodes de "nuit". Nous allons donc définir le jour comme la durée qui sépare deux passages consécutifs du Soleil à son point culminant, c'est-à-dire au "méridien" du lieu. Mais une telle durée est variable : pourquoi ?
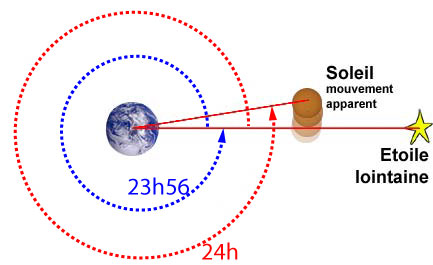
Définition du jour à partir de la rotation de la Terre autour de son axe
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou + image NASA
Tout d'abord, et nous le verrons plus loin (lois de Kepler), l'orbite apparente du Soleil autour de la Terre (en fait, l'orbite réelle de la Terre autour du Soleil) n'est pas un cercle mais une ellipse : ainsi la vitesse apparente du Soleil sur la sphère céleste va varier selon sa position sur sa trajectoire. Le Soleil passera donc au méridien soit en avance quand il va plus vite, soit en retard quand il ralentit, par rapport à une position moyenne. Pour que nos jours aient la même durée et donc que nos heures soient régulières (et que midi n'arrive pas un peu en avance ou un peu en retard), on construit une position moyenne théorique du Soleil sur l'année (le Soleil moyen, par opposition au Soleil vrai) qui définira le Temps moyen, échelle de temps qui a été en usage jusque dans les années 1970. La définition officielle de cette échelle de temps était : "l'heure légale en France est le temps moyen de Paris retardé de 9m 21s et augmenté de douze heures (c'est la définition du Temps Universel internationalement reconnu) et aussi augmenté de deux heures en été et d'une heure en hiver (c'est l'heure d'été ou l'heure d'hiver)". Le retard de 9m 21s sert à nous mettre à l'heure du méridien international (Greenwich). L'avance de douze heures sert à faire commencer le jour à minuit (c'est plus pratique car le temps moyen fait débuter le jour à midi au moment du passage du Soleil au méridien). Enfin le décalage d'une heure ou de deux heures nous donne l'heure d'été ou l'heure d'hiver. Les fuseaux horaires sont là pour permettre un décalage similaire pour les pays situés loin du méridien international.
Temps vrai, temps moyen
C'est cette différence entre le Soleil moyen et le Soleil vrai qui nous fait dire en janvier : "tiens, les jours rallongent plus le soir que le matin". En fait, c'est le midi vrai qui se déplace et arrive de plus en plus tard par rapport au midi moyen. Cet écart entre le midi moyen et le midi vrai est évidemment fondamental lorsque l'on construit un cadran solaire qui lui, va donner le temps vrai du lieu. Cette différence est appelée "équation du temps". Elle atteint 16 minutes au maximum fin octobre.
L'équation du temps est en fait la résultante de deux effets :
- l'équation du centre due à l'excentricité de l'orbite terrestre (la trajectoire de la Terre est une ellipse que l'on veut ramener à un cercle sur la sphère céleste) ;
- la réduction à l'équateur due à l'obliquité de l'écliptique (la Terre ne tourne pas dans son plan équatorial autour du Soleil) puisque l'on mesure le passage du Soleil au méridien du lieu par rapport au plan équatorial terrestre dans lequel il faut donc le ramener.
Plus simplement, disons que la Terre tourne autour de son axe dans le plan de l'équateur et autour du Soleil dans le plan de l'écliptique. C'est l'avance (ou le retard) du Soleil, par rapport à un mouvement uniforme dans l'écliptique, qui doit se projeter sur l'équateur.
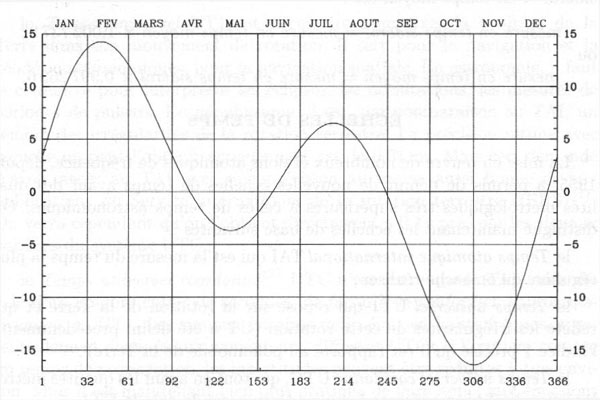
Equation du temps (en minutes) pour 1999
Crédit :
IMCCE/BDL

Concrétisation de l'équation du temps dans le ciel. L'image ci-dessus montre l'effet de l'équation du temps. On a superposé des images du Soleil prises de 10 jours en 10 jours le matin à la même heure.
Crédit :
Observatoire de Naucny/V. Rumyantser
Les échelles de temps
Du fait de l'augmentation de la précision dans la mesure du temps, les échelles utilisées ont rapidement évolué.
La rotation diurne de la Terre autour de son axe a longtemps semblé suffisamment uniforme pour servir de base à l'échelle de temps utilisée par les astronomes et appelée Temps universel. Dans cette échelle de temps, la seconde est définie comme étant égale à 1/86400 jour solaire moyen. Mais on s'est aperçu que la Terre ralentissait en constatant, par exemple, que la Lune s'éloignait de la Terre d'une manière qui n'était pas en accord avec les calculs théoriques. L'erreur ne provenait pas de ces calculs, mais du fait que le Temps universel n'était pas une échelle de temps uniforme.
Cela a conduit les astronomes à construire une autre échelle de temps fondée sur le mouvement orbital (révolution) de la Terre autour du Soleil. Cette nouvelle échelle de temps légalement en usage entre 1960 et 1967 s'appelle le temps des éphémérides. Elle est fondée sur l'observation de la longitude du Soleil dans le ciel au cours de l'année. L'équation qui définit numériquement la longitude du Soleil a été donnée par Newcomb et a été adoptée officiellement en 1952 par l'Union astronomique internationale. C'est un polynôme du second degré du temps. Si donc on observe la longitude du Soleil on en déduit aisément l'instant correspondant dans l'échelle de temps des éphémérides. En 1960 la onzième conférence générale des poids et mesures décida que la seconde est la fraction 1/31556925.9747 de l'année tropique pour le 0 janvier 1900 à 12 heures du temps des éphémérides.
La durée de l'année n'est cependant pas vraiment stable non plus et on a été amené à nouveau à changer d'échelle de temps. On utilise actuellement depuis 1967 une échelle de temps construite différemment, une échelle physique et non plus astronomique : on fabrique, à l'aide d'horloges atomiques (mesurant les fréquences des atomes), une "seconde" particulièrement stable. On va alors ajouter ces secondes les unes derrière les autres pour fabriquer une échelle de temps uniforme : le Temps atomique international, indépendant des mouvements célestes. Le Temps atomique international est une moyenne des horloges atomiques réparties dans le monde. Les effets relativistes montrent que cette seconde dépend du repère où l'on se place mais on arrive là à un niveau de précision très élevé et les solutions pour utiliser ces échelles de temps sont complexes.
L'utilisation du Temps atomique international, très stable, va entraîner un décalage avec la rotation de la Terre et il faudra recaler cette échelle de temps régulièrement pour que midi reste à midi... C'est pour cela que l'on annonce régulièrement qu'une seconde va être ajoutée de temps en temps le 31 décembre ou le 31 juillet, selon les variations de la rotation de la Terre, pour que l'échelle de temps atomique utilisée ne s'écarte pas de plus d'une seconde du temps astronomique qu'est le Temps universel. Cette échelle de temps atomique modifiée par l'ajout régulier d'une seconde s'appelle le Temps universel coordonné. L'échelle de temps stable et uniforme employée pour les calculs astronomiques est maintenant le Temps terrestre, échelle de temps dont la réalisation pratique est liée au Temps atomique international, et qui prolonge le Temps des éphémérides.
La précession et la nutation
Le ralentissement de la rotation terrestre nous a montré le caractère irrégulier de cette rotation. De plus, l'axe de rotation ne reste pas fixe au cours du temps : les perturbations gravitationnelles de la Lune, du Soleil et des planètes entraînent différents mouvements de cet axe. D'abord un mouvement oscillant "périodique" rapide de petite amplitude autour d'une position moyenne, c'est la nutation. Ensuite, un mouvement lent, "séculaire" : tout en restant incliné à peu près de 23° 26' sur l'écliptique (le plan orbital de la Terre), l'axe va effectuer une rotation complète en 26 000 ans. C'est la précession : dans 13 000 ans, l'étoile polaire aura changée. C'est l'étoile Véga vers laquelle pointera l'axe de rotation de la Terre et 13 000 ans plus tard il sera à nouveau dirigé vers notre étoile polaire.
La précession entraîne le déplacement rétrograde du point γ (équinoxe) le long de l'équateur céleste : il fera un tour en 26 000 ans. Les constellations vont donc sembler changer de place le long du zodiaque. Pour conserver les saisons à leur place chaque année nous devons donc considérer un équinoxe mobile.
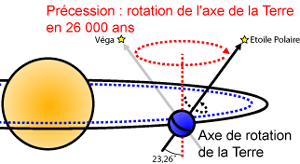
Le principe de la précession dûe au changement de direction de l'axe de rotation de la Terre
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
L'axe de rotation de la Terre subit de petites variations périodiques de sa direction : c'est la nutation.
Les implications de la précession
Ce mouvement de précession implique ainsi que l'équinoxe ou point vernal, va effectuer une rotation sur notre sphère céleste en 26 000 ans, c'est-à-dire que l'origine des ascensions droites que nous avons choisie sur notre sphère céleste est mobile ! Il ne sera guère pratique ainsi de mesurer les mouvements des étoiles sur notre sphère céleste... Le problème est résolu par le choix d'un équinoxe à une date donnée. Ainsi, aujourd'hui, le point vernal origine est celui du début de l'année 2000 : tous les catalogues d'étoiles utilisent cette référence et l'utiliseront encore pendant des années. Il est à noter que les observations sur le ciel peuvent, dans certains cas, se faire par rapport au point vernal du jour de l'observation et qu'une correction sera faite pour se ramener à un repère commun, celui de 2000.
Les positions dans un repère de la date sont dites coordonnées "vraies de la date" et celle dans un repère 2000 sont dites "moyennes J2000". Dans le premier cas, on utilise un axe affecté de la nutation et de la précession et dans le deuxième cas, on élimine la nutation (coordonnées moyennes) en prenant l'axe "moyen" du début de l'année 2000.
La précession va aussi compliquer la définition de l'année par rapport à "un tour" effectué par la Terre autour du Soleil.
Définition de l'année
L'année semble être facile à définir : c'est la durée nécessaire à la Terre pour faire un tour complet autour du Soleil. En fait ce n'est pas si simple. L'année intervient dans notre calendrier et le fait que la Terre ait accompli un tour complet (360°) n'est pas un critère fondamental.
- Si on prend une direction fixe dans l'espace, la Terre mettra 365 jours 6 h 9 m 10 s pour revenir dans cette même direction. On appelle cette durée l'année sidérale.
- Si on considère la direction du point vernal de la date (équinoxe de printemps), la Terre mettra 365 jours 5h 48m 45s pour revenir dans la direction de ce point. C'est une durée différente de l'année sidérale puisque le point vernal a bougé pendant que la Terre tournait... On appelle cette durée l'année tropique.
- Si on considère le point de l'orbite de la Terre le plus près du Soleil (le périgée, actuellement le 3 janvier) puisque l'orbite de la Terre est une ellipse, la Terre mettra 365 jours 6h 13m 53s pour y revenir. On appelle cette durée l'année anomalistique.
- Si on considère la direction du nœud de l'orbite lunaire, la Terre mettra 346 jours 14h 24m pour y revenir. On appelle cette durée l'année draconitique.
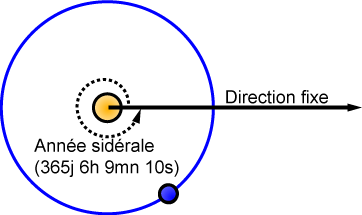
Les différentes façons de mesurer une année. L'année sidérale qui mesure la durée mise par la Terre pour faire 360° autour du Soleil, n'est pas l'année la plus couramment utilisée. C'est l'année tropique qui garantit le retour des saisons à la même date qui est la plus utilisée.
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
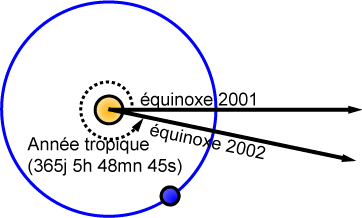
Les différentes façons de mesurer une année. L'année sidérale qui mesure la durée mise par la Terre pour faire 360° autour du Soleil, n'est pas l'année la plus couramment utilisée. C'est l'année tropique qui garantit le retour des saisons à la même date qui est la plus utilisée.
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
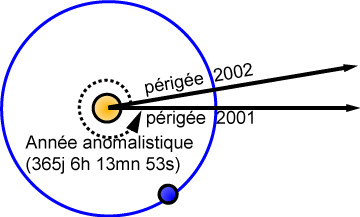
Les différentes façons de mesurer une année. L'année sidérale qui mesure la durée mise par la Terre pour faire 360° autour du Soleil, n'est pas l'année la plus couramment utilisée. C'est l'année tropique qui garantit le retour des saisons à la même date qui est la plus utilisée.
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
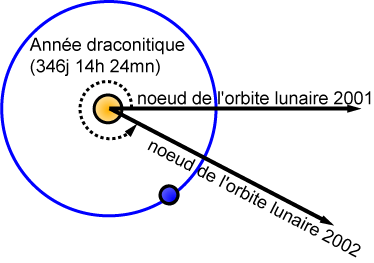
Les différentes façons de mesurer une année. L'année sidérale qui mesure la durée mise par la Terre pour faire 360° autour du Soleil, n'est pas l'année la plus couramment utilisée. C'est l'année tropique qui garantit le retour des saisons à la même date qui est la plus utilisée.
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
On voit que l'on a le choix pour définir une année. Ce choix sera dicté par des considérations sociales, culturelles et religieuses. Notre calendrier (grégorien) a adopté l'année tropique parce qu'elle fait revenir les saisons à la même date chaque année (calendrier solaire). Le calendrier chinois utilise l'année sidérale parce qu'il se cale sur le mouvement des astres dans le zodiaque (par rapport aux étoiles fixes). L'année draconitique ne sert que pour déterminer la périodicité des éclipses de Soleil. Les calendriers lunaires (comme le calendrier musulman) privilégient une bonne approximation des mois sur les lunaisons. Ils sont indépendants du mouvement de la Terre autour du Soleil.
L'heure
Qu'est-ce-que l'heure ?
L'heure nous permet de mesurer l'écoulement du temps au cours de la journée. Elle mesure une durée depuis le début du jour contrairement aux numéros des jours, des mois, des années, des siècles, des millénaires, qui indiquent un numéro d'ordre dans une chronologie.
La seule heure naturelle que nous pouvons percevoir est l'heure donnée par le Soleil liée à l'alternance jour-nuit : le Soleil nous indique le midi (c'est le moment où il est au plus haut dans le ciel) d'où nous déduisons le" minuit". Par convention, nous décomptons 24 heures au cours d'une journée de midi à midi ou de minuit à minuit. Pendant des siècles, l'heure du Soleil fut la seule accessible grâce aux cadrans solaires. On définit ainsi le temps solaire vrai en un lieu comme l'angle horaire du Soleil en ce lieu pour un instant donné. C'est une notion hybride qui traduit a la fois le mouvement de la Terre autour de son axe et son mouvement de révolution autour du Soleil et qui ne permet pas de déterminer des heures de longueur fixe.

Un cadran solaire
Crédit :
Danielle Briot
Histoire de l'heure
Dès l'aube de l'humanité l'homme a cherché à mesurer le temps pour prévoir le retour des saisons froides ou chaudes afin, par exemple, d'assurer sa subsistance. C'est l'alternance des jours et des nuits, donc le mouvement apparent du Soleil dans le ciel, qui va, entre autre, s'imposer à lui. Ce sont donc des considérations pratiques qui ont guidé les premières recherches sur le temps. Mais le concept de temps est aussi une question scientifique et philosophique de la plus haute importance. Cette quête fondamentale de connaissances conduit aujourd'hui les scientifiques à des recherches en physique de très haut niveau.
Historiquement on peut dire que la mesure du temps est essentiellement de nature astronomique. Elle ne deviendra l'affaire des physiciens que beaucoup plus tard, dans le courant du vingtième siècle.
Tous les phénomènes périodiques peuvent être utilisés pour définir une échelle de temps. Une idée vient donc naturellement en regardant le ciel : utiliser l'alternance des jours et des nuits, donc le mouvement du Soleil, comme phénomène de base pour construire une échelle de temps. L'utilisation du mouvement du Soleil est le principe de base de fonctionnement des cadrans solaires. Un des premiers cadrans qui nous soit parvenu est un cadran solaire égyptien qui date d'environ 1500 ans avant Jésus-Christ mais l'art des cadrans solaires, la gnomonique, ne connaîtra son apogée que vers les XVIème et XVIIème siècles.
Le temps donné par les cadrans solaires est ce que l'on appelle en astronomie le temps solaire vrai d'un lieu. Ce temps est donc un temps local qui n'est pas uniforme à cause de la non uniformité du mouvement du Soleil dans le ciel. Cela tient au fait que le Soleil vrai se déplace sur une orbite elliptique suivant les lois de Kepler, dans le plan de l'écliptique. Ce temps fût d'un usage très courant jusqu'au XVIIIème siècle. Le développement rapide des moyens de communication rendit cependant obligatoire l'adoption d'un temps solaire moyen. Ce temps solaire moyen est donné par un soleil moyen (fictif) se déplacant sur une orbite circulaire, à vitesse constante, dans le plan de l'équateur céleste. Ce temps solaire moyen est à l'origine de la première définition astronomique de la seconde jusqu'en 1960 : c'était la 86400ème partie du jour solaire moyen. La différence entre temps solaire moyen et temps solaire vrai s'appelle l'équation du temps.
Les variations du temps solaire vrai par rapport au temps solaire moyen sont de nature essentiellement géométrique. Newton est probablement le premier à avoir pensé à la non uniformité du mouvement de la Terre puisqu'il mentionne explicitement dans son livre des Principes (1686) que les astromomes doivent corriger le temps vrai fourni par l'observation du Soleil de l'équation du temps. Il ajoute également : "il se peut qu'il n'existe aucun mouvement uniforme par lequel le temps puisse être mesuré avec précision". Kant en 1754 puis Lalande en 1771 émettront des doutes quant à l'uniformité du mouvement de rotation de la Terre, et par voie de conséquence de celui du Soleil dans le ciel. On sait aujourd'hui que la rotation de la Terre n'est pas uniforme : le frottement des marées océaniques sur l'écorce terrestre, les variations saisonnières d'origine météorologique sont des causes maintenant bien connues de non uniformité de la rotation terrestre.
Une heure pour tous

Une gare au XIXème siècle : l'horloge de la gare n'indique pas l'heure locale mais l'heure de Paris.
L'heure solaire présente cependant plusieurs inconvénients : tout d'abord elle est locale, c'est-à-dire qu'elle dépend du lieu où on se trouve. Ensuite, elle n'est pas uniforme du fait de l'excentricité de l'orbite terrestre. Ce dernier inconvénient a été résolu en utilisant un temps moyen résultant d'une moyenne sur une année dont on connait l'écart au temps solaire vrai par l'équation du temps. Il reste encore le problème d'une heure qui dépend du lieu où on se trouve. Ce problème a été résolu au XIXème siècle sous l'impulsion des compagnies de chemins de fer. On a trouvé préférable d'utiliser la même heure partout, l'heure de Paris définie par le temps civil de Paris, défini lui, comme étant le temps moyen de Paris augmenté de 12 heures. Cette stipulation vient du fait que le temps moyen fait commencer le jour à midi (c'est le seul instant observable), ce qui n'est pas pratique dans la vie de tous les jours...
L'heure légale en France
Selon la loi du 9 mars 1911 en vigueur jusqu'en 1978, l'heure légale en France était l'heure du temps moyen de Paris retardée de 9 minutes 21 secondes. Cette définition voulait signifier en fait que l'heure en France était le temps universel. La loi de 1911 a été remplacée par le décret du 9 août 1978 qui stipule que "le temps légal est obtenu en ajoutant ou en retranchant un nombre entier d'heures au temps universel coordonné". Un décret fixe ce nombre pour chaque partie du territoire de la République Française en fonction des fuseaux horaires. Il peut l'accroitre ou le diminuer pendant une partie de l'année. Ce nouveau décret prévoit donc l'usage d'une heure d'été, apparue pour la première fois en 1916. C'est cette heure qui est diffusée par l'horloge parlante que l'on peut appeler par téléphone au 36 99.
Le temps universel
Le principe d'un temps unique pour un pays, réglé sur le temps moyen de l'une des villes, pose à nouveau le problème de coordonner une heure dans le monde entier. Mais s'il est possible d'imposer l'heure de Paris dans toute la France (l'écart au temps solaire vrai ne dépasse pas 30 minutes environ), il sera plus difficile de l'imposer au reste du monde du fait du décalage au temps solaire vrai qui ira grandissant en s'éloignant du lieu de référence. Cela a amené les états à se mettre d'accord pour définir un temps universel, référence pour tous, et des temps locaux qui ne différeraient que d'un nombre entier d'heures, par la création de "fuseaux horaires".
Le temps universel est donc une échelle de temps universelle, comme son nom l'indique. Par convention internationale, le temps universel est le temps moyen de Greenwich, augmenté de 12 heures (pour faire commencer le jour à minuit et non pas à midi).
En savoir plus: les échelles de temps
 En savoir plus
En savoir plus
Le Temps atomique international TAI est une échelle scientifique que les astronomes utilisent pour l’interprétation dynamique des mouvements des astres naturels et artificiels. Aucun signal horaire ne le diffuse directement. Mais on verra plus loin, à propos du temps universel coordonné, comment on peut dater les observations en TAI, l’exactitude relative étant de 10 à 20 nanosecondes ;
Le Temps universel UT1 est nécessaire pour fixer la position de la Terre dans son mouvement de rotation. Il sert pour la navigation et la géodésie astronomiques, pour la navigation spatiale. En astronomie, il faut le connaître pour interpréter les éclipses, les occultations, les mesures de périodes de pulsars. En géophysique, il est, par comparaison au TAI, un témoin des irrégularités de la rotation terrestre. La précision ultime avec laquelle on peut l’obtenir actuellement est de 0,01 ms. Mais ceci demande d’avoir accès au TAI avec une précision au moins aussi bonne et aux publications du Service International de la rotation terrestre (IERS)(1).
On verra cependant qu’on l’obtient directement à 0,1 s près par les signaux horaires du système UTC ;
Le Temps universel coordonné(2) UTC n’est autre que le TAI, mais décalé d’un nombre entier de secondes, de façon à se conformer approximativement au UT1. Les signaux horaires radio émis en haute fréquence, essentiellement destinés aux navigateurs, diffusent UTC ; si l’on tient compte du temps de propagation, les incertitudes peuvent être réduites à 1 ms environ. Mais il est maintenant bien plus pratique de faire appel aux émissions des satellites du « Global Positioning System » (GPS) ; avec des récepteurs appropriés on obtient en permanence et sans aucune correction UTC à 1 μs près environ. Si l’on a besoin d’une exactitude encore supérieure, il faut faire appel aux publications du Bureau international des poids et mesures (BIPM)(1) qui fournissent des corrections au temps du GPS. Les incertitudes sont alors réduites à 10 ou 20 ns. Ces méthodes donnent accès au TAI, après correction d’un nombre entier de secondes qu’il faut connaître. D’après les accords internationaux en vigueur, UTC ne doit pas s’écarter de plus de 0,9 s de UT1. Le tableau suivant donne la différence entre TAI et UTC depuis 1983.
| Intervalle de validité | TAI -UTC | TT - UTC |
|---|
| 1 juillet 1983 - 1 juillet 1985 | 22 s | 54,184 s |
| 1 juillet 1985 - 1 janvier 1988 | 23 s | 55,184 s |
| 1 janvier 1988 - 1 janvier 1990 | 24 s | 56,184 s |
| 1 janvier 1990 - 1 janvier 1991 | 25 s | 57,184 s |
| 1 janvier 1991 - 1 juillet 1992 | 26 s | 58,184 s |
| 1 juillet 1992 - 1 juillet 1993 | 27 s | 59,184 s |
| 1 juillet 1993 - 1 juillet 1994 | 28 s | 60,184 s |
| 1 juillet 1994 - 1 janvier 1996 | 29 s | 61,184 s |
| 1 janvier 1996 - 1 juillet 1997 | 30 s | 62,184 s |
| 1 juillet 1997 - 1 janvier 1999 | 31 s | 63,184 s |
| 1 janvier 1999 - 1 janvier 2006 | 32 s | 64,184 s |
| 1 janvier 2006 - 1 janvier 2009 | 33 s | 65,184 s |
| 1 janvier 2009 - 1 janvier 2012 | 34 s | 66,184s |
| 1 janvier 2012 - 1 janvier 2015 | 35 s | 67,184s |
| 1 janvier 2015 - 1 janvier 2017 | 36 s | 68,184s |
| 1 janvier 2017 - | 37 s | 69,184s |
Les temps en usage, transmis par exemple par les horloges parlantes et les stations de radiodiffusion des divers pays, dérivent de UTC par addition d’un nombre entier d’heures. UTC est donc la seule échelle de temps mondiale directement accessible aux observateurs et c’est celle dans laquelle doivent être datés les évènements scientifiques, en particulier les observations astronomiques. La plupart des émissions de signaux horaires radio diffusent suivant un code simple, uniformisé et audible une correction appelée DUT1 qui permet de corriger UTC pour avoir UT1 avec une erreur maximale de 0,1 s. Les utilisateurs qui veulent connaître UT1 avec une précision encore meilleure doivent faire appel aux circulaires de l’IERS qui donnent des tables des valeurs de UT1 – UTC. Pour avoir plus de détails, on peut consulter le Service international de la rotation tesrrestre ;
Le Temps des éphémérides TE fut la meilleure répresentation du temps uniforme avant l’apparition du temps atomique. Il reste, de ce fait, indispensable pour interpréter les observations anciennes. Pour les travaux sur les données récentes, il est remplacé par des échelles de temps liées au temps atomique dont la définition prend en compte les effets de la relativité générale. Ainsi les éphémérides géocentriques sont exprimées dans une échelle qui est en pratique TAI + 32,184 s. Cette échelle qui prolonge le TE, depuis le 1 janvier 1977, a reçu le nom de Temps terrestre, TT. En 2018, on a approximativement TT – UTC = 69,2 s. C’est cette valeur qui a été utilisée pour les calculs de cette édition de le "Guide des Données Astronomiques" . La figure 8 de l'ouvrage donne sous forme graphique les différences des échelles de temps par rapport au TAI. La figure 9 de l'ouvrage montre deux extraits détaillés ;
Le Temps dynamique barycentrique TDB est une échelle de temps-coordonnée recommandée par l’UAI en 1976 pour les éphémérides et les théories dynamiques rapportées au barycentre du système solaire. TDB diffère du temps terrestre TT par des termes périodiques et des termes de Poisson. En 1991, l’UAI a recommandé de remplacer TDB par le temps coordonnée barycentrique TCB.
------------------------------------------------------
(1) IERS central bureau, Richard-Strauss Allee 11, D 60598 Frankfurt/main, Allemagne. IERS-EOC, Observatoire de Paris, 61 avenue de l’observatoire, 75014 Paris.
(2) Lorsqu’il n’y a pas lieu de distinguer entre UTC et UT1, c’est-à-dire lorsqu’une précision d’une seconde suffit, la notation abrégée UT est admise. L’usage des initiales GMT (ou TMG) qui prête à confusion est fautif ; l’Union Astronomique Internationale a instamment demandé qu GMT soit remplacé par les désignations appropriées, UT1, UTC, UT. Cette Union a aussi recommandé les désignations TAI, UT1, UTC, UT dans toutes les langues.
Les fuseaux horaires
Chaque pays va définir son heure par l'écart au temps universel. Cet écart étant déterminé de façon à ce que l'heure adoptée respecte le cycle journalier lié au lever du Soleil, au midi, et au coucher du Soleil. Cependant, pour faciliter les changements d'heure pour les voyageurs, les accords internationaux prévoient d'adopter un écart au temps universel égal à un nombre entier d'heures. Pour cela, on définit 24 zones autour du globe appelées "fuseaux horaires". Chaque pays se rattache ainsi au fuseau le mieux adapté et définit son heure légale ou standard comme TU (temps universel) + ou - N heures (où N est un nombre entier). Cela ne l'empêche pas d'ajouter ou de retrancher une heure pour définir une heure d'été ou autre. Les pays très étendus en longitude adoptent plusieurs heures légales (par exemple aux USA, il y a 7 heures légales : Atlantique, Est, Central, Montagne, Ouest, Alaska et Hawaï, avec deux variantes : l'heure standard applicable en hiver et l'heure "de la lumière du jour" qui correspond à notre heure d'été puisqu'on l'applique en été en ajoutant une heure à l'heure standard).
On trouvera ci-dessous la répartition des heures légales selon les fuseaux horaires sur tous les continents. Remarquons que certains territoires comme le Groenland ou l'Antarctique n'ont pas d'heure légale propre : le Temps Universel y est donc utilisé. Remarquons aussi que tous les pays n'ont pas adopté un décalage d'un nombre entier d'heures avec le Temps Universel comme l'Inde qui a adopté 5h 30m. Les pays adoptant une heure d'été ajoutent une heure au décalage ci-dessous pour leur période d'été.
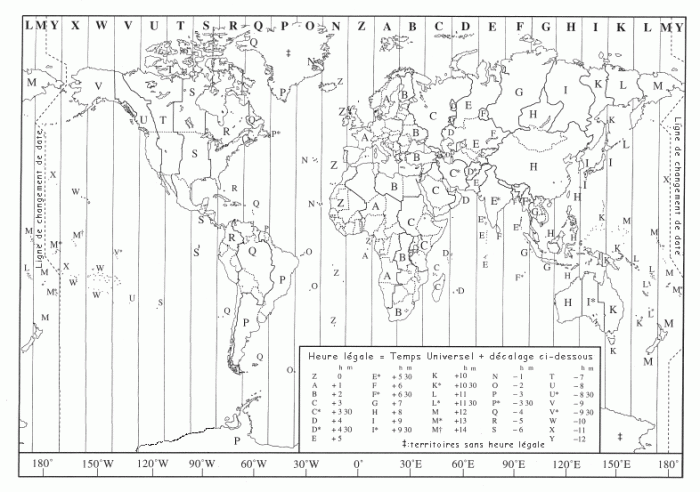
Les fuseaux horaires et les décalages par pays au 1 juin 2000
Crédit :
H.M.N.A.O. + IMCCE/BDL
La ligne de changement de dates
L'existence de fuseaux horaires va entraîner l'existence d'une "ligne de changement de date". Examinons en effet l'écart des heures locales au temps universel. En allant vers l'Est, le Soleil va se lever plus tôt et donc, pour obtenir les heures locales on va ajouter une heure, puis deux, puis trois au temps universel en se déplacant vers l'Est. En allant vers l'Ouest ce sera le contraire : on retirera des heures au temps universel pour que midi reste à 12 heures... En effet, s'il est midi en France, les pays situés à l'Est de la France sur une même latitude verront le Soleil vers la France, c'est-à-dire vers l'Ouest, c'est donc que ce sera l'après-midi et qu'il sera plus tard qu'en France et qu'on ajoutera une ou plusieurs heures à l'heure française pour obtenir l'heure locale.
Donc en allant vers l'Est on ajoute des heures : on arrive à la ligne de changement de date quand on a ajouté douze heures. S'il est midi en temps universel, il sera minuit le soir du même jour sur le dernier fuseau vers l'Est que l'on notera FE. En allant vers l'Ouest, on retranchera des heures et il sera 0 heure du même jour en arrivant sur le dernier fuseau vers l'ouest que l'on notera FO. Les deux fuseaux concernés sont en fait côte à côte et une heure plus tard, il sera 1 heure du même jour sur le fuseau FO et une heure du lendemain sur le fuseau FE qui vient de passer minuit. Le passage de la ligne de changement de date fait donc effectivement passer d'un jour à l'autre à une même heure ou plutôt à un même moment de la journée. Notons cependant que tout le monde est à la même heure et à la même date en temps universel, ce qui permet de s'y retrouver.
L'échelle de temps en physique
Une seconde "fabriquée"
C'est en 1955 que le premier étalon de fréquence fut construit par L. Essen et J. Parry qui travaillaient au National Physical Laboratory de Londres. Ces premiers travaux ouvrirent la voie à une nouvelle définition de la seconde qui vit le jour en 1967 lors de la treizième conférence générale des poids et mesures. La seconde est la durée de 9192631770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins F=3 et F=4 de l'état fondamental 6S1/2 de l'atome de césium 133. Malgré une complexité apparente au moins aussi grande que celle de la définition de la seconde de temps des éphémérides, cette définition offre l'avantage d'une bien meilleure accessibilité.
Un étalon primaire de fréquence
La mécanique quantique nous apprend que les atomes peuvent se trouver dans différents états ou niveaux d'énergie qui sont quantifiés. Autrement dit les valeurs de l'énergie des atomes prennent des valeurs discrètes et non continues. Le niveau d'énergie la plus basse sera appelé le niveau fondamental. Le niveau fondamental se décompose lui même en deux niveaux hyperfins notés respectivement F=3 et F=4. On sait également, depuis Max Planck, que pour faire passer un atome d'un niveau d'énergie à un autre, il faut lui apporter une énergie, sous forme de rayonnement électromagnétique, correpondant à la différence d'énergie des deux niveaux considérés. Des mesures réalisées entre 1955 et 1958 ont montré que l'atome de césium 133 pouvait passer du niveau hyperfin noté F=3 au niveau hyperfin noté F=4 lorsqu'il était soumis à un rayonnement micro-onde de fréquence 9192631770 Hz. C'est cette valeur qui est à la base de la définition de la seconde atomique. Un appareil électronique, un compteur de cycle, va donc compter 9192631770 cycles pendant une durée d'une seconde. L'appareil qui réalise ainsi la définition de la seconde atomique s'appelle un étalon primaire de fréquence. Il en existe actuellement différent types : les étalons primaires de fréquence à déflexion magnétique, à pompage optique et les fontaines atomiques. L'appareil qui compte les secondes et qui les accumule au cours du temps est une horloge atomique.
En savoir plus: les fontaines atomiques
 En savoir plus
En savoir plus
Les fontaines atomiques sont les derniers développements de la technique des étalons de fréquence. Ils utilisent la technique du refroidissement des atomes qui a valu son prix Nobel à C. Cohen-Tannoudji en 1997. En effet, et quel que soit l'étalon considéré, le nombre d'atomes qui subit l'interaction micro-onde est d'autant mieux déterminé que la durée d'interaction de ces derniers dans la cavité est plus important. Afin d'augmenter ce temps d'interaction les atomes sont piégés, confinés, dans six faisceaux lasers concourants afin de réduire le plus possible leur vitesse d'agitation thermique. La physique statistique nous enseigne en effet que la température d'un gaz est proportionnelle à la vitesse d'agitation des particules qui le compose. Si la vitesse est très faible la température correspondante sera très basse d'où le nom de la technique utilisée. Une fois les atomes confinés, ils vont être lancés en direction de la cavité micro-onde, comme dans les étalons classiques, à la seule différence que la cavité est cette fois verticale. La verticalité de la cavité s'impose à cause de la faible vitesse des atomes qui, s'ils effectuaient un vol balistique horizontal, "tomberaient vers le bas". Pour des raisons techniques (homogénéïté du champ magnétique...) la cavité micro-onde n'est pas réalisée en un seul morceau de longueur D à l'intérieur duquel aurait lieu, de façon continue, l'interaction. Dans le cas des étalons à déflexion ou à pompage une cavité dite de Ramsey est utilisée dans laquelle l'interaction a lieu en chacune de ses extrémités qui sont séparées par une distance D. Dans le cas de la fontaine atomique la cavité est encore un peu différente : il n'y a qu'une seule zone dans laquelle l'interaction micro-onde a lieu, mais deux fois de suite, une fois lorsque les atomes vont vers le haut et une fois lorsqu'ils vont vers le bas. La préparation et la détection des atomes de césium se fait comme dans le cas d'un étalon à pompage optique classique. La meilleure fontaine atomique actuellement en fonctionnement dans le monde, FO1, se trouve au Laboratoire primaire du temps et des fréquences, labaratoire du Bureau national de métrologie à l'observatoire de Paris.
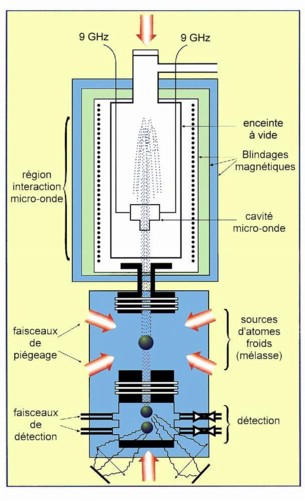
Crédit :
BNM/LPTF
Calcul du Temps atomique international TAI
Les horloges atomiques à césium sont des étalons primaires de fréquence très particuliers. Ils génèrent la seconde du système international comme dans le cas d'un étalon classique mais les accumulent également de façon à produire des minutes et des heures. La finalité de ces instruments est différente de celle des étalons. Alors que ces derniers doivent avoir une très bonne exactitude, une différence la plus faible possible entre la définition de la seconde du SI et la seconde réalisée par l'instrument, les horloges doivent avoir une excellente stabilité à long terme c'est à dire que les variations de la seconde produite doivent être les plus faibles possibles autour d'une valeur moyenne (qui n'est pas forcément très proche de la seconde du SI). Les principales horloges atomiques commerciales à césium sont du premier type étudié : ce sont des instruments à déflexion magnétique. D'autres horloges atomiques existent qui n'utilisent pas l'atome de césium. Il existe des horloges à rubidium, des horloges à quartz, des masers à hydrogène... C'est ce dernier type d'horloge, avec les horloges à césium, qui est le plus utilisé dans le calcul du temps atomique international. La 14ème Conférence générale des poids et mesures (CGPM) a décidé que le Temps atomique international est la coordonnée de repérage temporel établie sur la base des indications d'horloges atomiques fonctionnant dans divers établissements conformément à la définition de la seconde, unité de temps du Système international d'unités. C'est actuellement le Bureau international des poids et mesures qui est en charge du calcul du TAI. Cet organisme collecte les données d'environ 500 horloges (en 2016) réparties dans plus de 70 laboratoires. Le calcul du TAI est effectué à l'aide d'un algorithme, ALGOS, qui effectue une moyenne pondérée des lectures des horloges, la finalité étant d'obtenir une très bonne stabilité à long terme. L'exactitude de l'échelle de temps est assurée par des comparaisons régulières entre son intervalle unitaire et l'intervalle unitaire obtenu par les différents étalons primaires de fréquence répartis dans le monde. Ce mode de calcul permet d'obtenir une autre des propriétés attendues des échelles de temps : la pérennité. Une horloge qui cesse de fonctionner peut très facilement être remplacée par une autre sans que le comportement global du TAI en soit affecté. Actuellement l'instabilité du TAI est estimée à environ 4.10-15 à 10 jours, 4,3.10-15 à 40 jours, 4,5.10-15 à 160 jours et 10-14 au delà de 3 ans. Ces estimations sont effectuées à l'aide d'un estimateur statistique dénommé variance de Allan.
Comparaison d'horloges à distance
Il existe de nombreux organismes dans le monde qui possèdent des horloges atomiques ou des étalons primaires de fréquence. Bien sûr chacun de ces organismes souhaite comparer ses propres instruments à ceux des autres, à des fins d'évaluation et d'amélioration de leurs qualités métrologiques, ou simplement pour participer au calcul du temps atomique international, TAI . La méthode la plus classique pour comparer des horloges distantes consiste à employer les satellites du Global Positioning System, GPS.
Le GPS est un système militaire de radio-navigation constitué d'un ensemble de satellites en orbite à 20000 km autour de la Terre. Chaque station équipée d'une des horloges à comparer reçoit les signaux d'un satellite du GPS. Les temps d'arrivée des signaux sont datés grâce à l'horloge de la station réceptrice alors que les temps d'émission de ces signaux par un satellite quelconque sont datés dans l'échelle de temps de l'horloge embarquée par ce satellite. Un algorithme permet de faire la correspondance entre l'échelle de temps du satellite et le temps du GPS. En faisant une simple différence des observations effectuées aux mêmes instants dans les deux stations le temps du GPS disparaît et il est ainsi possible d'obtenir la différence de lecture des horloges des deux stations.
En savoir plus: la métrologie du temps
 En savoir plus
En savoir plus
Toutes les études entreprises en métrologie du temps ont bien sûr des applications. Dans le domaine de la recherche fondamentale on peut citer les tentatives de raccordement des unités du SI à la définition de la seconde car c'est l'unité qu'on sait, de loin, le mieux réaliser (incertitude relative de l'ordre de 10-15). Certaines constantes de la physique peuvent être déterminées par la seule mesure de la fréquence de phénomènes physiques, on peut alors obtenir leur valeur avec une très faible incertitude : la constante de Rydberg, le facteur de Landé de l'électron et la constante de structure fine en sont quelques exemples. La métrologie du temps a également un impact sur la physique atomique par le biais de la vérification de la linéarité de la mécanique quantique (équation de Schrödinger) et par sa contribution à la connaissance de certaines propriétés atomiques et moléculaires. La mesure du temps intervient également dans les tests des modèles de structure de l'espace-temps et de la gravitation par l'utilisation directe ou indirecte des étalons atomiques de temps. La finalité de ces tests est la discrimination des différentes théories de la gravitation, la relativité générale d'Einstein n'étant qu'une théorie parmi d'autres. La métrologie du temps trouve aussi sa place dans bon nombre d'applications de positionnement, de géodésie ou de navigation : le système GPS en est un exemple, le GLObal NAvigation Satellite System (GLONASS) ainsi que les systèmes DORIS (Détermination d'Orbite et Radio-positionnement Intégrés par Satellites) et PRARE (Precise Range Rate Equipment) en sont d'autres. La technique de radio-interférométrie à très longue base dite VLBI (Very Long Baseline Interferometry) trouve des applications dans l'étude de la rotation de la Terre et dans la formation des systèmes de référence céleste et terrestre.
Les mesures VLBI font appel à la stabilité de fréquence des masers à hydrogène présents dans les stations d'observation : c'est le domaine de la métrologie du temps. Les pulsars millisecondes sont des objets dont l'observation a démontré que leur stabilité de fréquence pouvait peut-être rivaliser avec la stabilité des meilleures échelles de temps atomique (TAI, TT(BIPM),...). Des études de très longue haleine sont en cours pour connaître la réponse à cette question. La métrologie du temps est doublement présente dans ces recherches. Premièrement parce que les temps d'arrivée des impulsions radio émises par ces astres sont datés par rapport à une horloge atomique présente dans la station d'observation. Deuxièmement parce qu'il faut raccorder cette horloge aux meilleures échelles de temps atomique à des fins de comparaison.
Les calendriers
Auteur: Jean-Eudes Arlot
Introduction
 Introduction
Introduction
Le repérage des instants exige la définition d'échelles de temps, mais indépendamment du choix d'une échelle, il faut définir un système de numérotation des jours (il est aisé de constater un changement de jour, il est plus difficile de constater un changement d'année ; ainsi le jour est l'unité naturelle). Ce système de numérotation a pour but de situer une date quelconque sans ambiguïté : c'est le problème de la chronologie.
La solution la plus simple, en principe, consiste à choisir arbitrairement un jour origine et à énumérer sans autre artifice les jours ultérieurs. Les époques antérieures peuvent être éventuellement repérées en énumérant vers le passé des jours que l'on dira être avant l'origine mais il est plus simple d'introduire un jour zéro et des nombres négatifs pour les jours situés avant l'origine. C'est en suivant ce principe que l'on a défini la période julienne.
Pour des raisons de tradition, mais aussi de commodité, on a été conduit à compliquer le système par un découpage en années et en mois. Les règles adoptées, qui constituent les divers calendriers, diffèrent d'une civilisation à une autre.
Chronologie et ères
Désignation des années
Pour les historiens, depuis le XVIIIème siècle, l'année qui précède l'an 1 de l'ère chrétienne est notée " 1 avant J.-C. " : elle est bissextile. Les années bissextiles se succédant tous les 4 ans, ce sont donc les années 1, 5, 9, ... avant J.-.C ; la règle de divisibilité par 4 ne peut plus s'appliquer.
Les astronomes, depuis J. Cassini (1740), utilisent une notation algébrique. Ils appellent année 0 l'an 1 avant J.-C. et comptent négativement les années antérieures. Ainsi :
... ... ...
2 après J.-C. = année 2
1 après J.-C. = année 1
1 avant J.-C. = année 0 (bissextile)
2 avant J.-C. = année -1
3 avant J.-C. = année -2
4 avant J.-C. = année -3
5 avant J.-C. = année -4 (bissextile)
6 avant J.-C. = année -5
... ... ...
C'est la notation des astronomes qui est utilisée dans les calculs d'éphémérides. Par rapport à la notation des historiens elle présente deux avantages :
- la règle de divisibilité par 4 des années bissextiles est conservée, les années 0, -4, -8, ... sont bissextiles.
- le calcul du nombre d'années qui sépare une année négative d'une année positive s'effectue algébriquement.
Ainsi le nombre d'années écoulées entre le 1 janvier -44 et le 1 janvier 1991 est égal à : 1991 - (-44) = 2035.
Ce système de numérotation des années ne dépend pas du calendrier. Pour l'ère chrétienne, c'est le calendrier julien qui est utilisé par les historiens pour les dates anciennes et, aussi, pour celles qui sont antérieures à sa création (-44).
Dans ce cas, ils utilisent un calendrier fictif ayant les mêmes règles de construction.
Début des siècles et des millénaires
De même que l'on numérote les années, on numérote les siècles et les millénaires. Le siècle représente une période de 100 ans, le millénaire une période de 1000 ans. Le premier siècle commence le 1 janvier de l'an 1 et se termine le 31 décembre de l'an 100. Le XXème siècle commence le 1 janvier 1901 et s'achève le 31 décembre 2000. Le XXIème siècle a commencé le 1 janvier 2001.
Le premier millénaire se termine le 31 décembre de l'an 1000. Le deuxième millénaire commence le 1 janvier 1001, le troisième millénaire commence le 1 janvier 2001.
Comment définit-on les calendriers ?
Les calendriers sont fondés sur des considérations de caractère astronomique.
Le mois est la durée approximative d'une lunaison, intervalle de temps entre deux nouvelles lunes.
L'année est une approximation de l'année tropique, intervalle de temps qui sépare deux passages consécutifs du Soleil à l'équinoxe de printemps.
Un calendrier est de type lunaire ou solaire selon que l'on privilégie l'approximation du mois ou de l'année.
Dans un calendrier lunaire la durée moyenne du mois doit être une bonne approximation de la lunaison (29,530589 jours), alors que dans un calendrier solaire la durée moyenne de l'année doit être une bonne approximation de l'année tropique (365,242190 jours) qui suit les saisons
Ainsi, le calendrier grégorien qui est notre calendrier usuel est solaire. Il en est de même pour les calendriers julien et copte.
Par contre, le calendrier musulman est lunaire et le calendrier israélite luni-solaire.
Chaque calendrier se définit une origine à partir de laquelle on va compter, en général, les années. Cela correspondra à une ère.
Correspondance entre les calendriers
Eres
Indépendamment de l'organisation des jours en mois et en années, chaque calendrier a besoin d'une origine pour compter en général des années (ce peut être des jours dans le cas de la période julienne) ou des groupes de plusieurs années comme les olympiades helléniques qui comptent 4 ans. Une telle origine définit une Ère.
L'ère chrétienne a débuté le 25 décembre de l'an 753 de la fondation de Rome (d'après Varron) mais le début de l'année sera le premier janvier pour concorder avec le calendrier de l'époque. Les calendriers grégoriens et juliens se situent actuellement dans l'ère chrétienne. Le calendrier julien a été en vigueur du premier janvier de l'an 45 avant J.-C. (an 709 de l'ère de la fondation de Rome, année bissextile) à l'an 1582 de l'ère chrétienne et le calendrier grégorien est en vigueur depuis l'an 1582 de l'ère chrétienne. L'usage de l'ère chrétienne a été introduite en 532 sur une proposition du moine Denys le Petit. C'est lui qui proposa, en 525, au pape l'expression "Anno Domini" (AD). Cet usage se répandra rapidement dans les textes et documents liturgiques, mais il faudra attendre plusieurs siècles (le règne de Pépin le Bref et celui de Charlemagne) pour que cet usage devienne courant dans la société.
L'ère de Dioclétien a débuté le 29 août 284 (julien). C'est l'origine du calendrier copte encore en usage dans la communauté copte d'Egypte.
L'Hégire a débuté le vendredi 16 juillet 622 (julien) qui est donc l'origine du calendrier musulman.
L'ère judaïque a débuté le 7 octobre -3760 (julien) qui est l'origine du calendrier israélite.
L'ère des Français a débuté le 22 septembre 1792 et s'est terminé le 1 janvier 1806 et a été utilisée par le calendrier républicain.
L'ère de la période julienne commence le 1 janvier 4713 avant J.-C. à midi (calendrier julien).
L'ère hellénistique compte une succession d'olympiades qui correspondent à quatre années. Elle a commencé avec le solstice d'été de l'an 776 avant J.-C. En l'an 1 de l'ère chrétienne, la 195ème olympiade hellénique a débuté en été.
D'autres calendriers se réfèrent à des ères plus incertaines quant à leurs origines. C'est le cas des calendriers :
- hindou, ère saka débutant le 3 mars 78 après J.-C. mais codifiée en 1957 et utilisé dans le calendrier indien (voir ce calendrier) ;
- hindou, ère samvat débutant le 23 février 57 après J.-C. ;
- tamoul, cycle nirâyana de 60 ans non différenciés depuis l'an 397 après J.-C. ;
- cambodgien et laotien, petite ère birmane partant du 21 mars 638 après J.-C. ;
- cambodgien et laotien, ère bouddhique débutant en avril-mai de l'an 544 avant J.-C. (mort de Bouddha d'après la tradition cinghalaise) ;
- chinois et vietnamien, cycles de 60 ans identifiés aux règnes des empereurs.
En savoir plus: la période julienne
 En savoir plus
En savoir plus
La période julienne est une échelle de temps qui numérote, sans discontinuité, les jours depuis le lundi 1 janvier -4712 à 12 heures.
Cette période julienne a été introduite par l'astronome Scaliger en 1583. Il nomme "julienne" cette numérotation en hommage à son père qui se prénomait Julien.
Date julienne : c'est la durée écoulée depuis le 1 janvier -4712 à 12 heures. On l'exprime en jour et fraction décimale de jour.
Jour julien : c'est la partie entière de la date julienne.
Le jour julien 0 commence le 1 janvier -4712 à 12h, le jour julien 1 commence le 2 janvier -4712 à 12h, le jour julien 2451911 commence le 1 janvier 2001 à 12h.
La continuité des jours dans la période julienne permet de calculer un intervalle de temps sans risque d'erreur même s'il couvre plusieurs calendriers. Ainsi le 1 janvier 1001 à 0h (calendrier julien) correspond à la date julienne 2086673,5; le 1 janvier 2001 à 0h (calendrier grégorien) correspond à la date julienne 2451910,5. Il s'est donc écoulé entre ces deux dates :
2451910,5 - 2086673,5 = 365237 jours.
Calendriers
Le calendrier julien
Définition
Le calendrier julien est, dans ses principales dispositions, conforme au calendrier romain réformé par Jules César. Dans l'usage moderne, on l'emploie avec l'ère chrétienne dont l'an 1 fut la 47e de cette réforme julienne.
Ce calendrier est de type solaire. Il comporte deux sortes d'années, les années communes de 365 jours, divisées en 12 mois de 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30 et 31 jours, et les années bissextiles de 366 jours dans lesquelles le deuxième mois est de 29 jours. Les années bissextiles sont celles dont le millésime est divisible par 4 ; une année sur 4 est donc bissextile.
La durée moyenne de l'année julienne (365,25 jours) est une approximation médiocre de celle de l'année tropique (365,242190 jours). Il en résulte que les dates des saisons se décalent d'environ 3 jours tous les 400 ans, soit d'un mois tous les 4000 ans.
Le calendrier julien a été en usage dans la plupart des nations d'Europe jusqu'au XVIème siècle. Il a été remplacé ensuite par le calendrier grégorien mais il est encore utilisé de nos jours pour déterminer les fêtes religieuses orthodoxes.
Le calendrier grégorien
Définition
C'est notre calendrier usuel.
Le calendrier grégorien est de type solaire. Il a été créé en 1582 par le pape Grégoire XIII pour corriger le retard que prenait le calendrier julien sur le Soleil, retard qui atteignait 10 jours au moment de cette réforme.
Ce calendrier est défini par rapport au calendrier julien de la manière suivante : le lendemain du jeudi 4 octobre 1582 (julien) fut le vendredi 15 octobre 1582 (grégorien), la succession des jours de la semaine étant respectée.
Le calendrier grégorien ne diffère du calendrier julien que par la répartition entre années communes (365 jours) et années bissextiles (366 jours).
Les années bissextiles sont les mêmes que celles du calendrier julien (année dont le millésime est divisible par 4) sauf trois années séculaires sur quatre, celles dont le millésime est multiple de 100 sans l'être de 400. Ainsi, les années 1700, 1800, 1900 sont communes alors que l'année 2000 est bissextile.
La durée moyenne de l'année est de 365, 2425 jours. Elle est très voisine de celle de l'année tropique (365,242190 jours).
Le calendrier grégorien a été adopté dès 1582 en Italie, en Espagne, au Portugal et dans les Pays-Bas catholiques. En France la réforme a été appliquée en décembre 1582, le lundi 20 décembre succédant au dimanche 9 décembre. En Grande-Bretagne, c'est seulement en 1752 que le 14 septembre a succédé au 2 septembre et que le calendrier grégorien a été adopté.
Adopté progressivement jusqu'au début du XXème siècle par tous les pays, ce calendrier est maintenant en usage dans le monde entier.
En savoir plus: le calendrier copte
 En savoir plus
En savoir plus
Ce calendrier est de type solaire. L'année se compose de douze mois de 30 jours, suivis, trois années de suite, de 5 jours complémentaires dits épagomènes et la 4ème année de 6 jours épagomènes. La durée moyenne de l'année (365,25 jours) est donc la même que dans le calendrier julien.
Ce calendrier définit l'ère de Dioclétien dont l'origine (1 Tout de l'an 1) correspond au 29 août 284 julien. Les années de 366 jours correspondent à celles dont le millésime plus 1 est multiple de 4. L'année copte commence le 29 ou le 30 août julien.
Ce calendrier est encore utilisé de nos jours en Egypte.
Mois de l'année copte
| 1 |
Tout |
| 2 |
Bâbah |
| 3 |
Hâtour |
| 4 |
Keihak |
| 5 |
Toubah |
| 6 |
Amchîr |
| 7 |
Barmahât |
| 8 |
Barmoudah |
| 9 |
Bachnas |
| 10 |
Bou'nah |
| 11 |
Abib |
| 12 |
Masarî |
En savoir plus: le calendrier musulman
 En savoir plus
En savoir plus
Le calendrier musulman a été adopté, sous sa forme actuelle, vers 632 après J.-C. Il définit l'ère musulmane dont l'origine, 1er jour de l'an 1 (Hégire), correspond au vendredi 16 juillet 622 julien.
C'est un calendrier de type lunaire. Les années sont de 12 mois. Le cycle lunaire des musulmans est de 30 ans.
Il comporte 19 années communes de 354 jours et 11 années abondantes de 355 jours. D'une année à l'autre le début de l'année musulmane se décale donc de 10 à 12 jours par rapport aux saisons (en moyenne de 10.875523... jours par an).
A l'intérieur d'un cycle les années abondantes sont les années numérotées 2, 5, 7, 10, 13, 16, 18, 21, 24, 26, 29.
Le cycle actuel a commencé le 1 Mouharram de l'an 1411 de l'ère musulmane qui correspond au mardi 24 juillet 1990.
Les mois sont d'une durée de 30 et 29 jours alternativement, le premier mois de l'année étant de 30 jours et le dernier de 29 jours (année commune) ou 30 jours (année abondante). La durée moyenne du mois (29,530556 jours) est voisine de celle de la lunaison.
|
Nom des mois |
Nombre de jours |
| 1 |
Mouharram |
30 jours |
| 2 |
Safar |
29 jours |
| 3 |
Rabi'-oul-Aououal |
30 jours |
| 4 |
Rabi'-out-Tani |
29 jours |
| 5 |
Djoumada-l-Oula |
30 jours |
| 6 |
Djoumada-t-Tania |
29 jours |
| 7 |
Radjab |
30 jours |
| 8 |
Cha'ban |
29 jours |
| 9 |
Ramadam |
30 jours |
| 10 |
Chaououal |
29 jours |
| 11 |
Dou-l-Qa'da |
30 jours |
| 12 |
Dou-l-Hidjja |
29 ou 30 jours |
Le calendrier musulman présenté ici est théorique.
Il existe d'autres variantes utilisant une chronologie différente. La date origine est parfois fixée au 15 juillet 622 ; selon certains auteurs la 15ème année du cycle lunaire est abondante et la 16ème commune.
Il arrive aussi que pour la détermination des fêtes religieuses, le début du mois soit défini par l'observation du premier croissant de lune suivant la nouvelle lune. Les calendriers sont alors locaux et dépendent des conditions d'observation.
En savoir plus: le calendrier israélite
 En savoir plus
En savoir plus
Le calendrier israélite remonte, sous sa forme actuelle, au IVème siècle après J.-C.
Il est de type luni-solaire. Il assure une durée moyenne du mois (29,530594 jours) très voisine de celle de la lunaison en utilisant des mois d'une durée de 29 ou 30 jours.
Il assure aussi une durée moyenne de l'année (365,2468 jours) voisine de celle de l'année tropique en faisant alterner 12 années communes de 12 mois et 7 années embolismiques de 13 mois à l'intérieur d'un cycle de 19 ans.
Dans chaque cycle les années embolismiques sont celles numérotées 3, 6, 8, 11, 14, 17 et 19. Le cycle actuel a commencé le 1 Tisseri de l'an 5739 qui correspond au lundi 2 octobre 1978.
Les années communes peuvent durer 353, 354, ou 355 jours et les années embolismiques, 383, 384, ou 385 jours. Les trois espèces d'années ainsi définies sont dites, respectivement, défectives, régulières ou abondantes.
La date origine du calendrier israélite est le 1 Tisseri de l'an 1. Elle correspond au 7 octobre -3760 julien.
|
Nom des mois |
Nombre de jours |
| 1 |
Tisseri |
30 jours |
| 2 |
Hesvan |
29 ou 30 jours |
| 3 |
Kislev |
29 ou 30 jours |
| 4 |
Tébeth |
29 jours |
| 5 |
Schébat |
30 jours |
| 6 |
Adar |
29 ou 30 jours |
| 7 |
Nissan |
30 jours |
| 8 |
Iyar |
29 jours |
| 9 |
Sivan |
30 jours |
| 10 |
Tamouz |
29 jours |
| 11 |
Ab |
30 jours |
| 12 |
Elloul |
29 jours |
Dans les années embolistiques, on intercale le mois de Véadar de 29 jours entre les mois d'Adar et de Nissan.
En savoir plus: le calendrier républicain (1)
 En savoir plus
En savoir plus
L'ère des Français et le calendrier républicain ont été adoptés par la Convention Nationale lors de la séance du 5 octobre 1793 :
" L'ère des Français ... [ commence ] le 22 septembre 1792 de l'ère vulgaire, jour où le Soleil est arrivé à l'équinoxe vrai d'automne, ... à 9 heures 18 minutes 30 secondes du matin pour l'observatoire de Paris "
La définition du calendrier républicain adoptée est la suivante (décret du 5 octobre 1793) :
" Le commencement de chaque année est fixé à minuit, commençant le jour où tombe l'équinoxe vrai d'automne pour l'observatoire de Paris ".
" La première année de la République française a commencé à minuit 22 septembre 1792, et a fini à minuit séparant le 21 du 22 septembre 1793 ".
" L'année est divisée en douze mois égaux de trente jours chacun, après lesquels suivent cinq jours pour compléter l'année ordinaire, et qui n'appartiennent à aucun mois; ils sont appelés les jours complémentaires. "
" Chaque mois est divisé en trois parties égales de dix jours chacune, et qui sont appelées décades... "
" En mémoire de la révolution qui, après quatre ans, a conduit la France au gouvernement républicain, la période bissextile de 4 ans est appelée "la Franciade."
" Le jour intercalaire qui doit terminer cette période, est appelé jour de la Révolution. Ce jour est placé après les 5 jours complémentaires... "
Les 5 jours complémentaires sont appelés jours des sanculottides.
Les années bissextiles sont appelées années sextiles.
Malheureusement, la définition de ce calendrier comporte une contradiction : l'année commence le jour de l'équinoxe d'automne, et l'année sextile est intercalée tous les quatre ans.
Cette erreur ne sera jamais corrigée et sera un des arguments utilisés pour le retour au calendrier grégorien, le 1 janvier 1806 (11 nivôse an 14).
Cette incohérence ne pose pas de problème sur la période d'utilisation du calendrier républicain : la première contradiction serait apparue en l'an 19.
En savoir plus: le calendrier républicain (2)

Ci-dessus et ci-dessous, le mois "Pluviôse" du calendier républicain. Chaque jour correspond à une plante, un animal ou un objet usuel.
Crédit : Bureau des longitudes/IMCCE
 En savoir plus
En savoir plus
Noms des mois proposés par Fabre d'Eglantine à la séance de la Convention Nationale du 24 octobre 1793.
Automne : Vendémiaire, Brumaire, Frimaire
Hiver : Nivôse, Pluviôse, Ventôse
Printemps : Germinal, Floreal, Prairial
Ete : Messidor, Thermidor, Fructidor.
Les jours de la décade prennent les noms suivants :
Primidi, duodi, tridi, quartidi, quintidi, sextidi, septidi, octodi, nonidi et décadi.
En savoir plus: le calendrier indien
 En savoir plus
En savoir plus
Le calendrier national actuellement en usage en Inde est celui défini par le Comité de réforme du Calendrier (Calendar Reform Committee). Il est officiellement appliqué depuis le 22 mars 1957 (1 Chaitra 1879 de l'ère Saka). La numérotation des années se fait dans l'ère Saka.
Les mois du calendrier indien comptent 30 ou 31 jours. Ils sont donnés ci après :
| Mois du calendrier indien |
Date grégorienne du premier mois |
| Chaitra (30 ou 31(*) jours) |
22 ou 21(*) mars |
| Vaisakha (31 jours) |
21 avril |
| Jyaistha (31 jours) |
22 mai |
| Asadha (31 jours) |
22 juin |
| Sravana (31 jours) |
23 juillet |
| Bhadra (31 jours) |
23 août |
| Asvina (30 jours) |
23 septembre |
| Kartika (30 jours) |
23 octobre |
| Agrahayana (30 jours) |
22 novembre |
| Pausa (30 jours) |
22 décembre |
| Magha (30 jours) |
21 janvier |
| Phalguna (30 jours) |
20 février |
(*) : pour les années bissextiles
La règle des années bissextiles est la même que pour le calendrier grégorien.
En savoir plus: le calendrier perpétuel
 En savoir plus
En savoir plus
Un calendrier perpétuel permet de déterminer le jour de la semaine correspondant à une date donnée.
CALENDRIER PERPETUEL
Le tableau de la page suivante permet de déterminer le jour de la semaine correspondant à une date donnée de l'ère chrétienne, et aussi de résoudre d'autres problèmes faisant intervenir les mêmes éléments.
MODE D'EMPLOI
La première colonne, intitulée Indice, donne les indices relatifs à tous les éléments de la ligne à laquelle ils appartiennent.
Pour obtenir le jour correspondant à une date donnée, on relève les indices relatifs :
- au chiffre des centaines, à celui des dizaines et à celui des unités de l'année considérée,
- au mois et au quantième de la date,
- et l'on fait la somme de ces cinq indices. Le reste de la division par 7 de cette somme est l'indice du jour cherché.
Pour les années bissextiles, on utilise les mois de janvier et de février suivis de la lettre B.
Suivant la parité du chiffre des dizaines de l'année, on utilise l'une ou l'autre des deux colonnes relatives au chiffre des unités. Pour faciliter l'opération, les chiffres des dizaines et des unités sont écrits en italique lorsque les dizaines sont impaires.
 Exemple
Exemple
|
2 janvier 1975 |
12 février 1944 |
| centaine |
19, indice : 1 |
19, indice : 1 |
| dizaine |
7, indice : 0 |
4, indice : 5 |
| unité |
5, indice : 1 |
4, indice : 0 |
| mois |
janv., indice : 0 |
fév. B, indice : 2 |
| quantième |
2, indice : 2 |
12, indice : 5 |
| Total |
4 |
13 |
| reste de la div. par 7 |
4 |
13 |
| jour cherché |
jeudi |
samedi |
- 1. Déterminer le jour correspondant à une date donnée à l'aide du tableau ci-dessus
- 2. Trouver les vendredis 13 de l'année 1948. Soit x l'indice du mois inconnu et k un entier positif ou nul, on a :
1 + 5 + 5 + x + 6 = 5 + 7 k ou x = 2,
les mois concernés sont Août et Février.
- 3. Quel était le troisième jeudi d'octobre 1951 ? (Réponse : le 18.)
- 4. En quelles années du XIXe siècle le 29 février est-il tombé un mardi ? (Réponse : 1820, 1848,1876.)
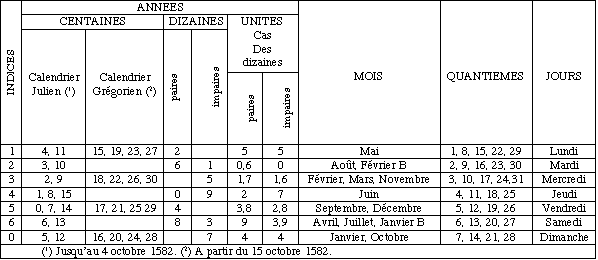
Les éphémérides
Auteur: Jean-Eudes Arlot
Introduction
 Introduction
Introduction
Dans le langage courant, l'éphéméride désigne ce qui se passe journellement ; l'éphéméride du jour est la liste des événements marquants de ce jour. Par extension, les éphémérides astronomiques désignent a priori une table journalière de positions de corps célestes mobiles (ceux du système solaire) ainsi que des phénomènes astronomiques ayant lieu ce jour telles les éclipses. Les éphémérides de positions sont donc avant tout la représentation d'un mouvement. Les éphémérides que l'on connaît sous forme de tables de nombres sont les plus courantes et les plus anciennes, mais ce n'est pas la seule forme possible et, de nos jours, ce n'est plus la forme la meilleure car il en existe maintenant d'autres beaucoup plus performantes.
Pour obtenir une éphéméride, il est nécessaire de disposer :
- d'un modèle théorique (dynamique ou cinématique) du mouvement du corps considéré ;
- d'observations de ce corps pour ajuster le modèle ;
- d'une représentation du mouvement pour donner les positions souhaitées à l'utilisateur.
La qualité d'une éphéméride pour la représentation d'un mouvement dépend de deux facteurs : utiliser un petit nombre de données (éviter des tables gigantesques) et ensuite avoir une bonne précision (commettre l'erreur la plus faible possible par rapport à la position "vraie" que l'on veut décrire).
Qu'est-ce qu'une éphéméride ?
Modèles théoriques des mouvements
Depuis les débuts de l'astronomie, modéliser le mouvement des corps du système solaire a toujours été un défi. Il s'est agi tout d'abord d'extrapolations empiriques des observations réalisées ; les premières tables proviennent ainsi d'une analyse purement cinématique des mouvements observés. La précision de ces premières tables est évidemment médiocre et ne progresse qu'avec l'amélioration de la précision des observations.
Viennent ensuite des prédictions fondées sur des théories gravitationnelles dont les paramètres sont déduits d'observations. A partir de Newton, les lois dynamiques sont connues et il importe alors de mettre en équation et de tenir compte de tous les effets gravitationnels qui peuvent agir sur les corps. Les recherches théoriques de Lagrange relatives au problème planétaire ont conduit à modéliser l'évolution à long terme des orbites par un système différentiel linéaire qui couple les excentricités et les inclinaisons. C'est un résultat fondamental. On consultera les cours relatifs aux lois de Kepler et à la mécanique céleste pour approfondir ces notions.
Histoire des éphémérides
Des recueils de prédictions diverses liées au calendrier, appelés almanachs ou éphémérides existaient dès le XIVème siècle. Citons :
- les tables alphonsines, faites sur l'ordre d'Alphonse X de Castille à partir de l'Almageste vers 1250 et qui arrivèrent à Paris en 1320 ;
- les éphémérides de Regiomontanus couvrant les années 1475-1506 ;
- les tables pruténiques construites en 1551 par Reinhold sur la base des travaux de Copernic ;
- les éphémérides des satellites de Jupiter de Simon Marius en 1614 ;
- les tables rudolphines en 1627 construites sur la base des travaux de Kepler et Tycho Brahé.
Les premières éphémérides vraiment destinées aux astronomes pour faire progresser notre connaissance du système solaire et de la Terre apparurent avec la Connaissance des Temps dont le premier volume parut à Paris en 1679. Ce premier volume se bornait à annoncer aux astronomes les principaux phénomènes et à leur fournir les calculs nécessaires aux réductions de leurs observations journalières. On y trouvait les levers et couchers du Soleil, de la Lune et des cinq planètes connues, Mercure, Vénus, Mars, Jupiter et Saturne, leurs passages au méridien de Paris, leurs longitudes, leurs latitudes et leurs déclinaisons. Au XVIIIème siècle, Lalande construisit ensuite les tables du Soleil et des planètes qui servirent de base aux éphémérides publiées dans la Connaissance des Temps jusqu'en 1808. En 1767 paraît à Londres le Nautical Almanac and Astronomical Ephemeris, éphéméride de même nature destinée également à contribuer à l'amélioration de l'astronomie, de la Géographie et de la Navigation.
Au cours des années 1770-1825, Laplace étudie les conséquences de l'application de la loi de la gravitation de Newton sur le mouvement des corps du système solaire et résout plusieurs problèmes concernant les théories planétaires. La plupart des tables du Soleil et des planètes utilisées dans la Connaissance des Temps durant la première moitié du XIXème siècle, sont issues de ses travaux.
La représentation de ces éphémérides a évolué au cours du temps. Jusqu'à la fin du XVIIIème siècle, la Connaissance des Temps présentait les éphémérides des astres mois par mois, le Soleil de jours en jours et les planètes de six jours en six jours. A partir de 1838, les éphémérides sont publiées corps par corps. Elles sont journalières pour le Soleil, de trois jours en trois jours pour Mercure, de six jours en six jours pour Vénus et Mars, de huit jours en huit jours pour Jupiter, de dix jours en dix jours pour Saturne et de quinze jours en quinze jours pour Uranus. En 1863, les éphémérides deviennent journalières pour Mercure, Vénus, Mars, Jupiter et Saturne et de quatre jours en quatre jours pour Uranus et Neptune.
Les éphémérides ont subi de nos jours d'importantes transformations. En 1980, la présentation des éphémérides sous forme de tables interpolables a été remplacée par une représentation en polynômes de Tchebychev beaucoup plus compacte et bien adaptée au développement de la micro-informatique.
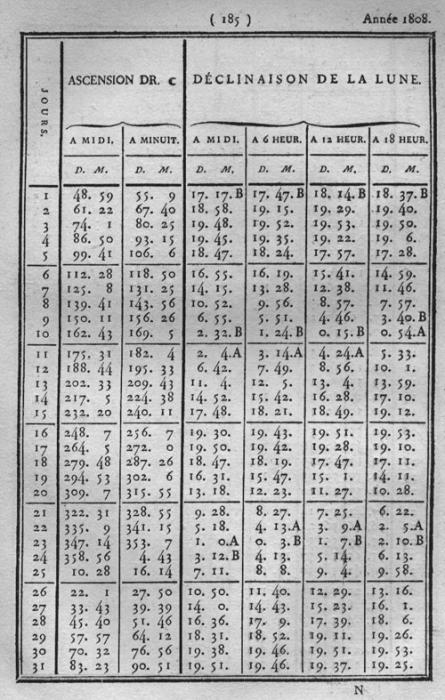
L'ascension droite et la déclinaison de la Lune dans la Connaissance des Temps pour l'année 1808.
Les valeurs sont données de 12h en 12h pour l'ascension droite et de 6h en 6h pour la déclinaison. La précision reste faible du fait de la rapidité du mouvement de la Lune.
Crédit :
Bureau des Longitudes
Les différents types d'éphémérides
Les éphémérides de position
Selon la quantité à représenter dans les éphémérides, on est amené à choisir un plan fondamental et des coordonnées. Pour les éphémérides destinées à l'observateur terrestre, le plan fondamental sera l'équateur terrestre et on fournira l'ascension droite (angle compté habituellement en heures vers l'est à partir de l'équinoxe de 0 à 24 heures, le long de l'équateur terrestre) et la déclinaison (angle compté habituellement en degrés vers le nord au-dessus du plan équatorial). On donne aussi le rayon vecteur, distance du centre du repère à l'astre considéré : il ne dépend pas du repère, sauf en ce qui concerne la prise en compte du temps de lumière.
Les éphémérides de la Lune, du Soleil et des planètes principales donnent des coordonnées apparentes pour le pointage des télescopes. Pour Pluton, les astéroïdes et les comètes, on donne les coordonnées astrométriques directement comparables aux catalogues d'étoiles. Dans le cas des satellites naturels proches des planètes, on donne des coordonnées tangentielles relatives à la planète dans un plan tangent à la sphère céleste, directement comparables aux clichés photographiques ou aux images provenant des caméras CCD.
Citons aussi les coordonnées topocentriques, centrées sur un observateur situé sur la surface terrestre : ces coordonnées ne peuvent être que calculées à la demande et on passe en général des coordonnées apparentes aux coordonnées topocentriques par une petite correction si nécessaire.
Certaines positions sont données dans des coordonnées non pas sphériques mais rectangulaires, l'axe X étant dirigé vers l'équinoxe du repère et l'axe Z vers le pôle nord céleste de ce repère. Des éphémérides données ainsi sont plutôt destinées à la navigation spatiale.
Ephémérides pour les observations physiques
Pour observer de la Terre à un instant donné des points situés à la surface d'un astre du système solaire, il faut définir les paramètres qui caractérisent la rotation de l'astre autour de son axe, donner leurs valeurs numériques et définir les systèmes de coordonnées par rapport auxquels ces points seront repérés sur cet astre (repère planétographique). On calcule ensuite les données qui permettent de connaître quels sont les points de l'astre qui sont visibles de la Terre à l'instant considéré. Il est également utile de connaître des quantités liées à l'éclairement du disque apparent.
L'Union Astronomique Internationale publie régulièrement les paramètres qui permettent de définir la rotation des corps ainsi qu'un système de coordonnées pour situer le relief ou les structures de surface de ces corps.
Le pôle nord est, par définition, celui des deux pôles de l'axe de rotation qui se trouve au nord du plan invariant du système solaire (plan proche de l'écliptique). Les longitudes sont comptées à partir du méridien origine mais dans le sens opposé à la rotation. Il résulte de ceci que, pour un observateur lointain, la longitude planétographique du centre du disque apparent augmente toujours avec le temps, quel que soit le sens de rotation de l'astre. Afin de respecter une tradition historique et de pouvoir continuer à utiliser des cartes anciennes, on admet en général des exceptions à cette règle quand il s'agit de la Terre, du Soleil et de la Lune dont les rotations sont directes.
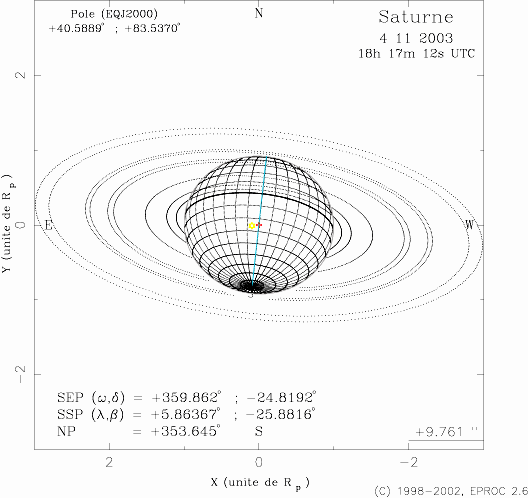
Aspect de la planète Saturne et de ses anneaux le 4 novembre 2003 à 18h17m12s UTC en unités "rayon de Saturne"
SEP = lonitude et latitude planétocentriques de la Terre en degrés
SSP = longitude et latitude planétocentriques du Soleil en degrés
NP = angle de position du pôle Nord de la planète par rapport au pôle Nord céleste en degré
Crédit :
I.M.C.C.E.
Le repérage des éphémérides de position
Les systèmes de référence
La connaissance des positions et des mouvements des astres nécessite d'avoir des notions précises des systèmes de référence de coordonnées spatiales et temporelles où l'on va situer les positions décrites par les éphémérides. Nous avons vu précédemment que l'argument temps des éphémérides ne pouvait être pris dans n'importe quelle échelle de temps. De même, nous allons voir que les coordonnées spatiales à utiliser doivent être rattachées à un système de référence grâce à un repère de référence.
On distingue les systèmes de référence célestes et terrestres.
Les systèmes de référence célestes sont soit dynamiques (basés sur l'étude dynamique des mouvements des corps du système solaire) soit cinématiques (basés sur l'étude statistique des mouvements des corps lointains tels que les étoiles, les galaxies et les quasars). Les systèmes de référence célestes dynamiques, tout d'abord construits dans la mécanique newtonienne, le sont aujourd'hui dans la mécanique relativiste qui lie l'argument temps aux variables spatiales. Pour les besoins des éphémérides actuelles, les définitions que nous avons données pour l'argument temps des éphémérides sont suffisantes. Pour rattacher les positions des corps célestes à un observateur situé sur la Terre, on a besoin de définir également un système de référence terrestre.
Les systèmes de référence terrestres nécessitent la connaissance d'un modèle de Terre, de sa forme et de ses déformations au cours du temps. La détermination d'une position topocentrique nécessite de disposer d'un tel système pour connaître la position du lieu en question par rapport aux positions que l'on a dans le système céleste. Les éphémérides étant en général géocentriques, les positions des corps célestes doivent être définies d'abord dans un système de référence céleste.
Les repères de référence célestes
Un système de référence est un concept théorique et la construction d'éphémérides nécessite la connaissance d'un repère de référence qui est la matérialisation concrète d'un système de référence. Un repère de référence céleste sera donc associé à des théories dynamiques, à des constantes et à des catalogues d'étoiles.
Un repère de référence se définit par un plan de référence et par une direction privilégiée. Pour les éphémérides publiées actuellement, le plan de référence est l'équateur de la Terre (repère équatorial) ou l'écliptique, plan de l'orbite de la Terre autour du Soleil (repère écliptique). La direction de référence est celle de l'équinoxe, nœud ascendant de l'écliptique sur l'équateur, intersection des deux plans. Ces plans et cette direction sont liés à la Terre et nous allons définir différents repères de référence selon les théories et les constantes utilisées pour les construire, puis, pour chaque repère ainsi construit, nous allons fixer les plans et la direction de référence pour obtenir un repère parfaitement défini.
Les repères cinématiques liés aux étoiles
Ces repères sont définis par les positions et les mouvements propres des étoiles. Citons les catalogues FK4 et FK5 qui utilisent 1535 étoiles. Des repères utilisant par exemple les étoiles du catalogue Hipparcos et des radiosources très lointaines sont utilisés comme catalogue pour l’astronométrie. Ils seront supplantés par le catalogue issu de la mission GAIA en cours de construction. Deux versions de ce catalogue existent déjà (2018).
Les repères dynamiques liés aux corps du système solaire
Les modèles dynamiques des corps du système solaire ajustés sur les observations radar ou laser sont indépendantes des étoiles des catalogues et définissent un plan et une direction de référence. Associés à une théorie de la précession - nutation, ils définissent un repère. Citons le repère lié aux intégrations numériques « DE430/DE431 du Jet Propulsion Laboratory ou encore INPOP de l’IMCCE et celui lié aux théories analytiques ELP2000/VSOP87 de la Lune et des planètes du Bureau des longitudes.
Les systèmes de coordonnées
Une fois défini un repère de référence, il faut choisir les coordonnées à utiliser pour fournir des positions dans les éphémérides.
A un repère de référence donné, on associe une théorie de la précession - nutation et on définit :
- les positions dans le repère moyen (les plans fondamentaux sont ici des plans moyens, c'est-à-dire affectés de la seule précession). Une date doit être donnée pour fixer le repère mais cette date est conventionnelle (par exemple 1950 pour le repère FK4 et 2000 pour le FK5) ;
- les positions dans le repère vrai (les plans fondamentaux sont affectés de la précession et de la nutation). La date du repère est celle à laquelle on donne les positions : le repère n'est pas fixe. C'est le seul repère accessible directement par un observateur terrestre.
Dans le repère ainsi défini, les coordonnées peuvent être :
- géométriques : ce sont les positions occupées réellement par le corps considéré à l'instant donné, sans tenir compte de la vitesse de la lumière ;
- apparentes : ce sont les positions vues par un observateur placé au centre du repère. Elles sont rapportées à un repère vrai de la date. On tient compte de la vitesse de la lumière et de l'aberration annuelle.
- astrométriques ou astrographiques : ce sont des coordonnées directement comparables aux catalogues d'étoiles. Elles se déduisent des coordonnées apparentes par la transformation de précession - nutation pour se ramener à un repère fixe (de la date du catalogue d'étoiles) et par la suppression de l'aberration annuelle. Le temps de lumière est toujours pris en compte.
Les coordonnées sont en général données sous forme sphériques, c'est-à-dire sous forme d'ascension droite et de déclinaison dans le repère équatorial ou sous forme de longitude et de latitude dans le repère écliptique. Elles peuvent être données sous forme d'angle horaire à la place de l'ascension droite pour un instant donné dans un repère local. Enfin, toujours dans un repère local, on peut donner l'azimut et la hauteur d'un astre à un instant donné. On consultera le cours sur la sphère céleste et les repères en astronomie pour plus de détails sur ces coordonnées.
Les coordonnées géométriques sont fournies sous forme cartésiennes X, Y, Z dans un repère équatorial, l'axe X étant dirigé vers le point vernal et l'axe Z vers le pôle Nord.
Enfin des coordonnées tangentielles ou différentielles peuvent être données pour des corps proches relativement l'un à l'autre sur un plan tangent à la sphère céleste.
Représentation des éphémérides
Les éphémérides sous forme de tables
La plus ancienne forme sous laquelle les éphémérides fournissent les positions des astres est une table de positions dont l'intervalle (une heure, un jour, un mois, ...) dépend de la vitesse de variation des valeurs de ces positions. Plus cette variation est rapide, plus petit doit être l'intervalle de temps séparant deux données successives. La simple lecture d'une table, accompagnée d'une interpolation à vue, suffit pour fournir une position permettant de repérer l'astre dans le ciel. Cependant, si l'on souhaite une précision plus grande, il faut effectuer une interpolation qui n'est plus linéaire, ce qui demande des calculs plus complexes à partir des valeurs publiées si celles-ci le permettent. Pour une précision plus grande, il faut diminuer l'intervalle entre deux positions et donc augmenter le volume de données publiées. L'Astronomical Almanac et le Guide des données astronomiques encore aujourd'hui, et la Connaissance des Temps jusqu'en 1979, contiennent des éphémérides sous forme de telles tables.
Citons le cas de la Lune : pour une précision de 0.01 seconde de degré, l'intervalle entre deux positions doit être de 3 heures ce qui conduit à la publication de 2920 valeurs annuellement par coordonnée. Citons aussi le cas des satellites galiléens de Jupiter qui ont un mouvement extrêmement rapide autour de Jupiter. Une éphéméride tabulée aurait nécessité un pas toutes les 20 minutes soit près de 30 000 valeurs pour une année! Cela conduit à un volume de données trop important pour être publié tel quel dans une éphéméride imprimée. D'autres solutions doivent être trouvées.
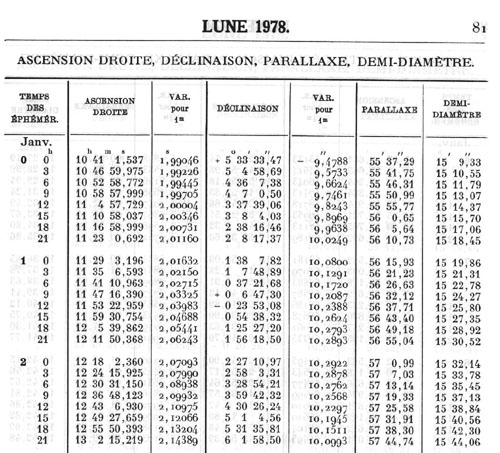
Un extrait de la Connaissance des Temps pour 1978 : l'ascension droite et la déclinaison de la Lune sont données de 3h en 3h avec la variation pour une minute. Le nombre de données à publier et les calculs d'interpolation à réaliser pour une précision correcte sont importants.
Crédit :
Bureau des Longitudes
En savoir plus: l'interpolation des éphémérides
 En savoir plus
En savoir plus
Une éphéméride est une table qui fournit, pour des dates particuières en principe équidistantes, les valeurs d'une ou de plusieurs fonctions qui décrivent l'évolution des positions des astres concernés, ou d'autres grandeurs relatives à ces astres. On appelle interpolation la technique de calcul qui permet d'évaluer les valeurs de ces fonctions pour des dates intermédiaires autres que celles qui figurent dans l'éphéméride.
Le cas le plus simple est celui où la fonction considérée varie assez lentement, ou est donnée avec assez peu de précision pour qu'aucun calcul ne soit nécessaire. On se contente alors d'une interpolation à vue (par exemple, magnitude de la planète Jupiter : aucun calcul n'est nécessaire, quand on examine l'éphéméride du chapitre 5, pour estimer que sa valeur est -1,8 le 2 juillet 2002).
Plus souvent, on devra employer l'interpolation linéaire et procéder comme suit. Soit :
t, l'instant pour lequel on veut calculer le fonction f ;
t1, l'instant immédiatement inférieur ou égal à t et figurant dans l'éphéméride, la valeur correspondante de f étant f1 ;
t2, l'instant immédiatement supérieur à t et figurant dans l'éphéméride, la valeur correspondante de f étant f2.
Alors, on calculera f par la formule :
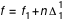
où
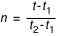 et
et 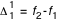
s'appellent respectivement facteur d'interpolation et différence première.
Dans certains cas, l'interpolation linéaire fournit un résultat trop imprécis. Pour s'en rendre compte, on forme le tableau suivant :

où t0, t1, t2, t3, etc sont des instants figurant dans l'éphéméride, et f0, f1, f2, f3, etc les valeurs correspondantes de la fonction f données par cette éphéméride. Les quantités :
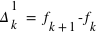
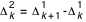 {k=0,1,2,...}
{k=0,1,2,...}
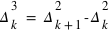
s'appellent respectivement différences premières, différences secondes, différences troisièmes, etc. L'interpolation linéaire est suffisante si les différences secondes sont inférieures à 4 unités du dernier ordre envisagé. Sinon (et à condition que les différences troisièmes n'excèdent pas 62 unités du dernier ordre envisagé, ce qui sera toujours le cas dans cet ouvrage), on emploie la formule de Bessel :
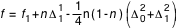
où n est le même facteur d'interpolation que plus haut, et, compte tenu des expressions ci-dessus :
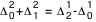
Les éphémérides sous forme graphique
Comme nous l'avons vu, les corps rapides comme les satellites de Jupiter ne peuvent avoir des éphémérides précises publiées annuellement. Une première solution consiste alors à offrir au lecteur une représentation graphique dont la lecture conduit à une précision de quelques dizaines de secondes de degré, précision bien faible mais suffisante pour identifier les corps lors d'une observation. On trouvera ci-dessous les configurations des satellites de Jupiter publiées par la Connaissance des temps. A gauche pour un mois de l'année 1808 et à droite pour 2000.

Crédit :
Bureau des Longitudes
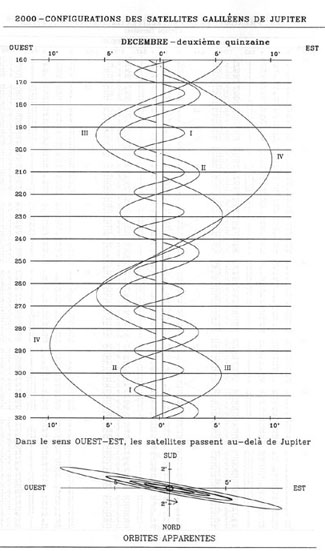
Crédit :
Bureau des Longitudes
Détermination de la configuration des satellites de Jupiter à une date donnée
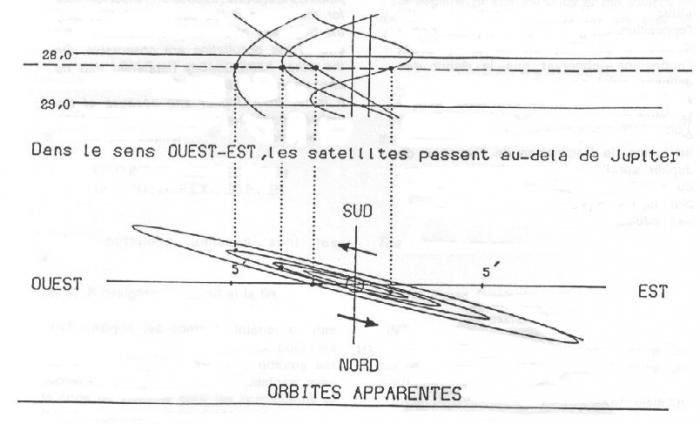
Crédit :
Bureau des Longitudes/Jean-Eudes ARLOT
Approximation d'une fonction par un polynôme
L'usage très répandu aujourd'hui des calculatrices de poche et des micro-ordinateurs permet d'utiliser une formulation plus complexe pour les éphémérides et on va chercher plutôt à conserver une précision de représentation optimale sur la période de temps couverte par l'éphéméride. Ainsi, au lieu d'évaluer une fonction f(t) sous la forme d'un tableau de valeurs calculées à des intervalles rapprochés du temps, on va établir des fonctions d'approximation de f(t) valables sur de grands intervalles de temps, en minimisant les erreurs et le volume global des données.
L'éphéméride veut donc représenter une fonction f(t) constituée, soit par le résultat d'une intégration numérique, soit par une fonction analytique du temps qui traduit le mouvement d'un corps ou l'évolution temporelle d'un phénomène. Or, on sait que toute fonction peut être approchée sur un intervalle de temps donné par un polynôme dont le degré et le nombre de termes sont d'autant plus élevés que l'intervalle de temps est grand. Une telle approximation n'est pas optimisée et le volume de données à publier est important mais l'utilisation d'une telle éphéméride est très simple puisqu'il suffit de substituer le temps dans les polynômes ainsi construits. D'autres représentations sont cependant bien meilleures.
En savoir plus: approximation de Tchebychev (1)
 En savoir plus
En savoir plus
Les fonctions que nous voulons approcher sont toujours définies pour toutes les valeurs de la variable temps. L'approximation lagrangienne par des polynômes consiste à faire passer, pour un intervalle donné, un polynôme de degré n par n+1 valeurs, alors qu'il serait préférable de tenir compte de toutes les valeurs de la fonction sur cet intervalle. L'approximation de Tchebychev s'impose pour cela, car elle est celle de plus bas degré dont l'erreur ne dépasse pas une valeur donnée a priori, et son erreur est régulièrement distribuée sur l'intervalle considéré.
La fonction d'approximation va se présenter comme une suite de développements en polynômes de Tchebychev sur une succession d'intervalles de temps. Ainsi le volume de données est réduit et le calcul des positions est rapide. Cette représentation est donc bien adaptée aux besoins des astronomes (amateurs, professionnels, théoriciens, astrométristes, ...).
Les éphémérides Tchebychev se présentent sous la forme d'une suite de coefficients a0, a1, ...an pour une coordonnée donnée sur un intervalle [t1, t2]. L'utilisation de ces éphémérides se fait de la manière suivante. Le calcul de la valeur de la coordonnée à l'instant t de l'intervalle [t1, t2] se fait en effectuant le changement de variable :
x=-1+{2(t-t1)}/{t2-t1}, donc x appartient à l'intervalle [-1, +1]
Les polynômes de Tchebychev de première espèce Tn(x) sont donnés par la relation :
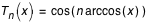
On peut aussi les calculer à l'aide de la relation de récurrence :
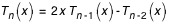 avec
avec 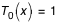 et
et 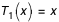
La coordonnée est alors égale à :
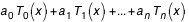
Dans la majorité des éphémérides -Soleil, Lune, planètes-, on a choisi des polynômes de Tchebychev pour la réalisation des éphémérides. Voyons maintenant comment calculer une position à partir de cette représentation.
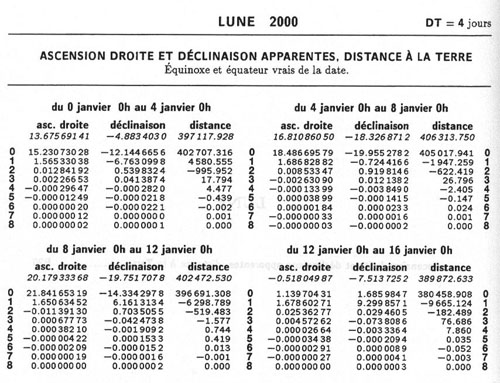
Crédit :
I.M.C.C.E.
Ci-contre, un extrait de la Connaissance des Temps pour l'année 2000 : l'ascension droite et la déclinaison sont fournies sous forme de coefficients : il faut programmer un petit formulaire simple pour calculer les valeurs pour tout instant de l'intervalle de validité. Les données à publier sont peu importantes et la précision des valeurs obtenues est la meilleure.
En savoir plus: approximation de Tchébychev (2)
 En savoir plus
En savoir plus
Soleil, Lune, Planètes
Soit t une date julienne appartenant à l'intervalle de temps t0, t0 + DT et y une coordonnée d'un astre. On calcule 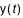 par la formule :
par la formule :
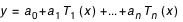
Où
- x est un paramètre compris entre -1 et +1 qui se déduit de t par la relation :
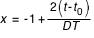
- a0, a1, ..., an sont les coefficients numériques publiés dans la Connaissance des Temps, valables pour l'intervalle de temps t0, t0 + DT contenant t :
- T1(x), ..., Tn(x) sont des polynômes de Tchebychev, en x, que l'on calcule :
- soit par la relation :
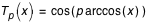 ;
; - soit par la relation de récurrence :
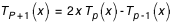 Avec :
Avec : 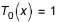 ;
; 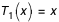
Caractéristiques générales
Les éphémérides de l'année sont publiées corps par corps. Pour chaque corps, on compte un certain nombre de variables qui pour des intervalles de temps donnés, sont représentées par des tableaux donnant les coefficients de leurs développements en polynômes de Tchebychev ou sous forme de fonctions mixtes.
En haut de chaque page, on trouve :
- le nom du corps concerné suivi de l'année de l'éphéméride ;
- le type des variables représentées ;
- éventuellement, les caractéristiques du système de coordonnées.
En bas de chaque page, on trouve les unités utilisées.
Les coefficients d'un tableau sont publiés en colonne. Pour chaque tableau, on précise :
- le nom de la variable représentée ;
- les dates de début et de fin de l'intervalle de temps correspondant au domaine de validité du tableau.
- la longueur des intervalles de temps DT (en jours) figure en haut de chaque page ;
- les coefficients sont notés 0, 1, ..., p,... n;
- la valeur de contrôle du tableau, imprimée en italique, figure en tête de chaque tableau. C'est la valeur y(t0) de la variable y représentée par le tableau, pour t0 début de l'intervalle de temps t0, t0 + DT. Elle est égale à :
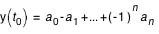
La valeur de contrôle permet de vérifier que les coefficients ont été correctement entrés en mémoire sur une calculette ou un calculateur. De plus, l'ensemble des valeurs de contrôle des tableaux d'une même variable donne une idée de l'évolution de cette variable au cours de l'année.
Calcul d'une coordonnée
Pour calculer la valeur d'une coordonnée d'un astre pour une date t exprimée en UTC, on commence par :
- effectuer, sur t, une correction déduite de la table 2 afin de se ramener à l'argument des éphémérides (identifié à TT) :
- chercher, parmi les tableaux représentant la coordonnée, celui qui correspond à l'intervalle de temps t0, t0 + DT dans lequel se trouve t. Il faut insister sur le fait que la représentation, qu'elle soit en polynômes de Tchebychev ou sous forme de fonctions mixtes, n'est pas valable en dehors de l'intervalle t0, t0 + DT.
Le calcul se poursuit de la manière suivante :
Soleil, Lune, Planètes
- On calcule x par la formule (2).
- A partir des n + 1 coefficients du tableau a0, a1, ..., ap, ..., an (notés 0, 1,... p, ..., n), on calcule la coordonnée y(t) par la formule (1).
- Les polynômes de Tchebychev tp(x) se calculent soit par la formule (3), soit par la relation de récurrence (4). Notons que, si on n'utilise que les p + 1 (p < n) premiers coefficients du développement en polynômes de Tchebychev, on commet, sur la représentation de y, une erreur au plus égale à la somme des valeurs absolues des n - p coefficients négligés.
- Pour avoir le temps de passage du Soleil au méridien origine en un jour donné, numéroté j dans le mois, on applique la même méthode en prenant t = j + 0,5.
En savoir plus: approximation de Tchébychev (3) exemple de calcul
 En savoir plus
En savoir plus
Exemple 1. Calculer le rayon vecteur héliocentrique de Mars le 5 Novembre 2003 à 16h 51m 42s UTC.
On effectue d'abord une correction pour se ramener à l'argument des éphémérides. Pour 2003, la valeur de TT - UTC n'est pas encore connue, mais on peut la prendre égale à 65 s. La date t est donc le 5 novembre 2003 à 16h 52m 47s argument des éphémérides.
On utilise les coefficients de la page B36 valables du 0 juillet 0h au 33 décembre 0h. Le calendrier des pages B148 et B149 donne les numéros JDA des jours de l'année correspondant au 0 juillet (JDA = 181) et au 5 novembre (JDA = 309). On a :
DT = 186 ;
t - t0 = 309 - 181 + 16h 52m 47s = 128.703 321 759 jours
On en déduit par la formule (2) :
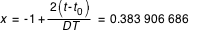
On peut calculer les polynômes de Tchebychev par l'un des deux algorithmes suivants :
Algorithme 1
Les polynômes de Tchebychev 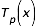 sont calculés par la relation (3) :
sont calculés par la relation (3) :
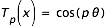 où
où 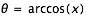
On a : θ = 67°.424 117 27. On en déduit :
T1(x)= cos (θ) = x = 0.383 906 686
T2(x)= cos 2(θ) = -0.705 231 314
T4(x)= cos 4(θ) = -0.005 297 589
T6(x)= cos 6(θ) = 0.712 703 365
T8(x)= cos 8(θ) = -0.999 943 871
Algorithme 2
Les polynômes 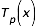 sont calculés par la relation de récurrence (4) :
sont calculés par la relation de récurrence (4) :
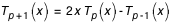
avec : 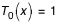 ;
; 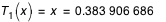
On en déduit :
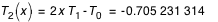 ,
,
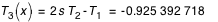 , etc
, etc
Les polynômes de Tchebychev étant déterminés, le rayon vecteur R de Mars se déduit de la formule (1) :
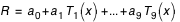 ,
,
Où les coefficients de a0, a1, ..., a9 sont ceux du tableau de la page B36 valables du 0 juillet 0h au 33 décembre 0h. On a donc :
R = 1.415 514 22 + 0.035 889 20 T1 + ... + 0.000 000 04 T9,
Soit finalement :
R = 1.412 255 01 ua.
Table des coefficients des polynômes de Tchébychev
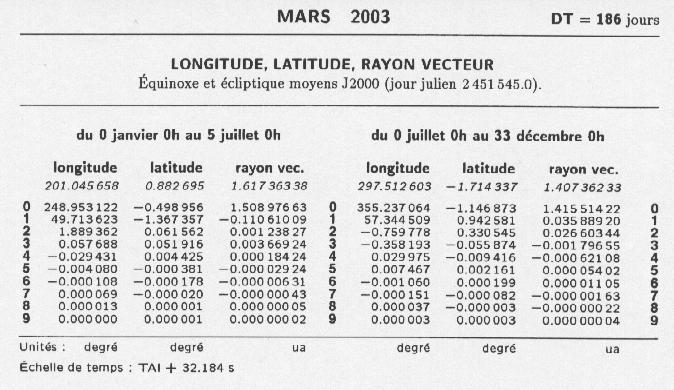
Crédit :
I.M.C.C.E.
En savoir plus: approximation par des fonctions mixtes (1)
 En savoir plus
En savoir plus
Comme nous l'avons vu, l'approximation polynomiale n'est pas la seule possible pour représenter une éphéméride. L'introduction des fonctions mixtes, permet de prendre en compte le caractère quasi-périodique des fonctions qui apparaissent dans les éphémérides. En effet, une fonction quasi-périodique à variations faibles sur un intervalle donné peut être approchée par un développement en polynômes de degré n peu élevé mais on n'a pas utilisé le fait que la fonction soit quasi-périodique sur l'intervalle considéré, ce qui est le cas du mouvement des corps du système solaire.
Voyons par un exemple comment en tirer parti.
Soit la fonction paire
f(x) = cos x + cos 2x
Elle est beaucoup mieux représentée avec la base de fonctions
1, cos x, cos 2x, cos 3x,... qu'avec la suite de polynômes
1, x2, x4, x6,... , ou toute autre base de polynômes pairs.
Si une éphéméride n'est jamais aussi simple dans la réalité, on peut toujours l'approcher par une combinaison de fonctions périodiques dont les périodes proviennent de la nature physique du phénomène (par exemple la périodede révolution d'un corps céleste), et de termes séculaires (polynômes du temps) qui témoignent du caractère non rigoureusement périodique du phénomène ou du mouvement décrit.
Le mode de représentation à l'aide des fonctions mixtes est très bien adapté à la représentation des mouvements des satellites naturels des planètes et des corps à période courte qui s'écartent peu, sur quelques périodes, d'un mouvement périodique, avec des variations d'amplitude et de fréquence lente par rapport à la période principale du corps et de ses multiples entiers.
Dans la Connaissance des Temps on trouve en particulier l'expression des coordonnées différentielles des satellites naturels des planètes sur des intervalles de temps couvrant une à quelques révolutions, avec des formules faciles à mettre en œuvre directement par l'utilisateur et qui se présentent ainsi :
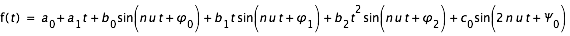 .
.
où 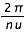 est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les φj et Ψj sont les phases (j = 0, 1, 2). Cette formule découle du choix de la base. Les termes mixtes sont de la forme : A tksin(p nu t + Ψ) (k et p entiers A : amplitude ; Ψ : phase). Sur un intervalle de temps donné les valeurs maximales de k et p sont ajustées en fonction de la précision recherchée. Si l'intervalle de représentation est élargi, il faudra enrichir la base de termes mixtes en puissance du temps et en multiples de la fréquence de base. Mais si l'intervalle de temps se rétrécit, il faut également modifier la base sous peine de perdre de la précision (ce n'est pas le cas avec la représentation à l'aide de polynômes dont la précision augmente quand l'intervalle diminue.
est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les φj et Ψj sont les phases (j = 0, 1, 2). Cette formule découle du choix de la base. Les termes mixtes sont de la forme : A tksin(p nu t + Ψ) (k et p entiers A : amplitude ; Ψ : phase). Sur un intervalle de temps donné les valeurs maximales de k et p sont ajustées en fonction de la précision recherchée. Si l'intervalle de représentation est élargi, il faudra enrichir la base de termes mixtes en puissance du temps et en multiples de la fréquence de base. Mais si l'intervalle de temps se rétrécit, il faut également modifier la base sous peine de perdre de la précision (ce n'est pas le cas avec la représentation à l'aide de polynômes dont la précision augmente quand l'intervalle diminue.
Voyons maintenant l'application des fonctions mixtes pour la représentation du mouvement d'un satellite de planète en révolution rapide.
En savoir plus: approximation par des fonctions mixtes (2)
 En savoir plus
En savoir plus
Satellites
Soit t une date julienne appartenant à l'intervalle de temps t0, t0 + DT. On calcule les coodonnées X et Y d'un satellite pour la date t par la formule (Chapront et Vu, 1984) :
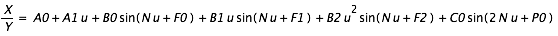 (5),
(5),
où :
- u = t - t0 ; u est compté en jours ;
- A0, A1, B0, F0, B1, F1, B2, F2, C0, P0 sont les coefficients numériques publiés dans la Connaissance des temps, valables pour l'intervalle de temps t0, t0 + DT contenant t ;
- N est la fréquence associée au satellite considéré. Elle est proche de celle du satellite lui-même, sauf dans le cas d'Hypérion pour lequel on prend une fréquence proche de celle de Titan du fait de l'existence d'un très gros terme perturbateur de fréquence plus grande que celle du satellite lui-même.
Caractéristiques générales
Les éphémérides de l'année sont publiées corps par corps. Pour chaque corps, on compte un certain nombre de variables qui, pour des intervalles de temps donnés, sont représentées par des tableaux donnant les coefficients de leurs développements en polynômes de Tchebychev ou sous formes de fonctions mixtes.
En haut de chaque page, on trouve :
- le nom du corps concerné suivi de l'année de l'éphéméride ;
- le type des variables représentées ;
- éventuellement, les caractéristiques du système de coordonnées.
En bas de chaque page, on trouve les unités utilisées.
Les coefficients d'un tableau sont publiés en colonne. Pour chaque tableau, on précise :
- le nom de la variable représentée ;
- les dates de début et de fin de l'intervalle de temps correspondant au domaine de validité du tableau.
Satellites
- la valeur de la fréquence N (en radians par jour) associée au satellite figure en haut de chaque page ;
- les coefficients sont notés A0, A1, B0, B1, F0, F1, B2, F2, C0, P0. Pour quelques satellites, certains coefficients ne sont pas donnés car ils sont nuls.
- A0, B0, C0 sont exprimés en secondes de degré par jour ;
- A1, B1 sont exprimés en secondes de degré par jour ;
- B2 est exprimé en secondes de degré par (jour)2 ;
- F0, F1, F2, P0 sont exprimés en radians ;
- dans la formule (5) u est compté en jours à partir du début de l'intervalle (époque t0).
Calcul d'une coordonnée
Pour calculer la valeur d'une coordonnée d'un astre pour une date t exprimée en UTC, on commence par :
- effectuer, sur t, une correction déduite de la table 2 afin de se ramener à l'argument des éphémérides (identifié à TT) ;
- chercher, parmi les tableaux représentant la coordonnée, celui qui correspond à l'intervalle de temps t0, t0 + DT dans lequel se trouve t. Il faut insister sur le fait que la représentation, qu'elle soit en polynômes de Tchebychev ou sous forme de fonctions mixtes, n'est pas valable en dehors de l'intervalle t0, t0 + DT.
Le calcul se poursuit de la manière suivante :
On applique la formule (5) avec 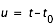 (u est compté en jours).
(u est compté en jours).
En savoir plus: Exemple de calcul
 En savoir plus
En savoir plus
Exemple 2. Calculer les coordonnées tangentielles de Téthys (troisième satellite de Saturne) par rapport à la planète, le 4 janvier 2003 à 23h 29m 57s UTC.
On effectue la même correction de 65s que dans l'exemple 1 pour se ramener à l'argument des éphémérides. La date t est donc le 4 janvier 2003 à 23h 31m 02s argument des éphémérides.
On utilise les coefficients de la page B120 valables du 0 janvier 0h au 16 janvier 0h. On a, pour X :
A0 = -0.001 000, A1 = 0.0
B0 = 50.188 200, F0 = 2.518 466, etc.
et, pour Y :
A0 = 0.002 100, A1 = 0.000 010,
B0 = 23.773 900, F0 = 1.092 443, etc.
On applique ensuite la formule (5) :
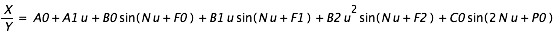 ,
,
où : N = 3.3280 radians/jours ;
u est le nombre de jours écoulés entre le 0 janvier à 0h et le 4 janvier à 23h 31m 02s, soit 4.979 884 jours. On obtient finalement :
X = 12".387,
Y = -21".897.
Table de coefficients de fonctions mixtes

Crédit :
I.M.C.C.E.
La précision des éphémérides
Lorsque l'on utilise une éphéméride pour calculer la position d'un corps du système solaire, on est amené à se poser la question : quelle est la précision de la quantité calculée ? Où se trouvera le corps observé par rapport à la position calculée ? On veut donc connaître la précision de l'éphéméride ou plutôt son exactitude. La précision des éphémérides est la résultante de trois types de précisions différentes :
- la précision interne de la théorie dynamique utilisée pour modéliser le mouvement et qui dépend de l'importance des termes des séries négligées et qui peut être évaluée à l'aide d'une comparaison à une intégration numérique (la précision interne est en général la meilleure) ;
- la précision externe de la théorie utilisée qui dépend de la précision des observations utilisées pour l'ajustement des constantes d'intégration de cette théorie et aussi de la répartition des observations au cours du temps (c'est la précision externe qui limite la précision globale des éphémérides) ;
- la précision de la représentation que l'on choisit en ajustant le nombre de coefficients et la longueur des intervalles de validité ou en interpolant une table (cette précision est la seule que l'on puisse choisir, elle ne doit pas dégrader la précision globale).
Aujourd'hui, la précision avec laquelle on peut positionner une planète ou un satellite de planète est la suivante :
| Soleil/Terre | 0,3" | 220 km |
| Mercure | 0,9" | 440 km |
| Vénus | 0,3" | 70 km |
| Lune | 0,008" | 15 m |
| Mars | 0,4" | 60 km |
| Jupiter | 0,5" | 1500 km |
| Satellites galiléens de Jupiter | 0,1" | 300 km |
| Saturne | 0,9" | 5400 km |
| Titan | 0,2" | 1200 km |
| Uranus | 0,5" | 6550 km |
| Neptune | 1,0" | 20 000 km |
| Pluton | 1,0" | 20 000 km |
A noter que pour les besoins de l'exploration spatiale, on est amené à construire des éphémérides de dernière minute plus précises mais se dégradant très rapidement dans le temps.
Les phénomènes astronomiques
Qu'est-ce qu'un phénomène astronomique ?
On appelle "phénomène astronomique" une configuration particulière des astres que l'on peut prévoir. Ce phénomène peut être perceptible sans instrument d'observation (éclipse de Lune ou de Soleil, lever d'un astre, ...). Les éphémérides vont donc prévoir ces phénomènes. Dans certains cas (éclipses de Soleil, lever et coucher d'un astre), la visibilité du phénomène est locale et les paramètres publiés dans l'éphéméride seront généraux. Il faudra prévoir des tables, des formules avec coefficients ou des graphiques pour savoir ce qui se passe dans un lieu précis.
Les principaux phénomènes donnés sont :
- les levers et couchers des astres
- les éclipses de Soleil et de Lune
- les passages de Mercure et Vénus devant le Soleil
- les phénomènes des satellites de Jupiter et de Saturne.
On se reportera au cours sur les éclipses pour le détail des calculs et des prédictions de ces phénomènes.
Lever et coucher d'un astre en un lieu donné
Lever et coucher des astres
Pour calculer l'instant du lever ou du coucher d'un astre dont on suppose connues les coordonnées équatoriales approchées α et δ au moment du phénomène considéré, on calcule d'abord l'angle horaire H au moment du lever ou du coucher par la formule :
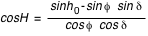 où
où
φ est la latitude du lieu et h0 un angle petit qui sera défini plus loin. Le temps sidéral approché du lever est alors :
(2a) 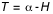 ;
;
et celui du coucher,
(2b) 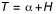 .
.
On calcule ensuite, à partir de T, l'instant du phénomène en temps universel comme on l'a expliqué dans les paragraphes précédents.
Si l'astre se déplace rapidement sur la sphère céleste (c'est le cas pour le Soleil, certaines planètes et surtout la Lune), on calcule pour l'instant trouvé des coordonnées α et δ plus exactes en interpolant les tables et l'on recalcule H puis T, par les formules (1) et (2), d'où l'instant du phénomène en UT. Pour la Lune, on est quelquefois amené à effectuer une itération supplémentaire.
Quant à h0, son expression générale est la suivante :
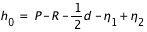 ,
,
P est la parallaxe. On la néglige pour tous les astres sauf pour la Lune pour laquelle P = 57'.
R est la réfraction à l'horizon. Les tables du présent volume utilisent la théorie de la réfraction de Radau qui conduit à R = 36'36", mais l'on pourra utiliser la valeur R = 34' adoptée dans les Ephémérides Nautiques publiées par le Bureau des longitudes et dans d'autres publications étrangères.
(1/2) d est le demi-diamètre apparent de l'astre. On l'introduit dans la formule quand on calcule le lever et le coucher du bord supérieur du Soleil et de la Lune et non pas le lever et le coucher du centre de l'astre. On prend, aussi bien pour le Soleil que pour la Lune, (1/2) d = 16'.
Si l'observateur est à une altitude A au-dessus du niveau de la mer, on introduit dans 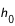 l'angle
l'angle 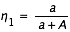 , où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
, où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
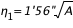 ,
,
A étant exprimé en mètres.
Si l'on cherche le lever ou le coucher d'un astre en un lieu dont l'horizon est limité par des collines ou des montagnes d'altitude 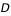 situées à la distance
situées à la distance 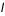 de l'observateur, on ajoutera à
de l'observateur, on ajoutera à 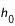 l'angle
l'angle 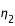 tel que :
tel que :
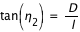 .
.
On ne cherchera pas à obtenir les instants du lever ou du coucher des astres avec une précision supérieure à une minute, la valeur exacte de la réfraction à l'horizon au moment du phénomène étant trop mal connue.
Calcul d'un coucher ou d'un lever d'un astre
Coucher à Bordeaux de l'étoile Sirius le 20 Avril 2002.
Les coordonnées moyennes de l'étoile pour 2002 sont (chapitre 10, "Positions d'étoiles") :
α = 6h 45m 15s ; δ= - 16°43'11".
En faisant les corrections de précession pour le 20 avril (données à la fin de ce chapitre), on trouve :
α = 6h 45m 16s, δ = 16°43'12".
Ici P = 0, (1/2) d = 0, η1 = 0, η2 = 0 ;
d'où :
h0 = -R = -34'
Les coordonnées de Bordeaux sont :
λ = + 2m 7s φ = + 44°50'7".
On déduit de la formule (1) :
cos H = 0,28411 d'où H = 73,494° = 4h 53m 59s.
Et le temps sidéral du coucher est :
T = α + H = 11h 39m 15s.
Le temps sidéral de Greenwich est donc :
T1 = T + λ = 11h 41m 22s
Le temps sidéral de Greenwich à 0h le 20 avril 2002 est T0 = 13h 51m 38s (chapitre "Positions du Soleil et de la Lune").
d'où :
Tt = T1 - T0 = 21h 49m 44s.
En convertissant cet intervalle de temps sidéral en un intervalle de temps moyen, on trouve que Sirius se couche à Bordeaux le 20 avril 2002 à :
t = 21h 46m 9s (UT)
Les phénomènes des satellites de Jupiter
Les satellites galiléens présentent des phénomènes particuliers dus aux positions que prennent le Soleil, Jupiter et la Terre : les éclipses (lorsqu'un satellite passe dans l'ombre de Jupiter) ; les occultations (lorsqu'un satellite passe derrière Jupiter par rapport à la Terre) ; les passages (lorsqu'un satellite passe devant Jupiter par rapport à la Terre) et les passages d'ombre (lorsque l'ombre d'un satellite passe sur le disque de Jupiter). Les phénomènes les plus célèbres sont les éclipses car ils sont les plus faciles à observer : il s'agit de l'extinction ou de l'apparition d'un satellite isolé. Les autres phénomènes nécessitent l'observation simultanée de Jupiter ce qui dégrade beaucoup le rapport signal sur bruit.
Tous ces phénomènes ont été observés visuellement pendant des dizaines d'années et le grand nombre d'éclipses observées a constitué la base des premières éphémérides. Dès la fin du XIXème siècle, les techniques d'observation des éclipses se sont améliorées et les premières courbes photométriques ont permis d'améliorer la précision de la datation de ces phénomènes. Ensuite, les enregistreurs photoélectriques sont apparus mais, malgré le progrès qu'ils apportaient, ils ont été très peu utilisés : ils sont arrivés lorsque cessa l'intérêt des astronomes pour ce type de travaux et n'ont pas encore été repris pour des raisons de précision.
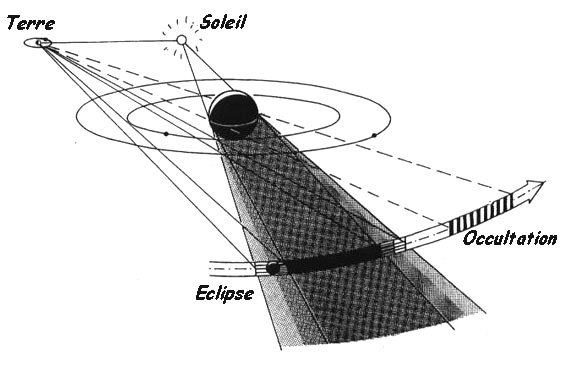
Les positions relatives de Jupiter, du Soleil et de la Terre pour que les satellites galiléens présentent des "phénomènes".
Crédit :
I.M.C.C.E./D.T. VU
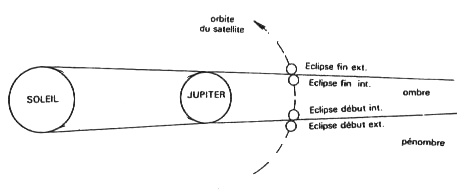
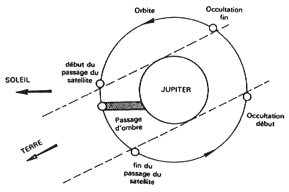
Configurations pour les différents types de phénomènes.
Crédit :
I.M.C.C.E./W. THUILLOT

Un passage d'ombres sur le disque de Jupiter.
Crédit :
Karkoshka et Murrell, NMSU
Où se procurer des éphémérides
Où trouver des éphémérides imprimées ?
Bien que la micro-informatique soit omniprésente pour les calculs astronomiques, les éphémérides imprimées sont encore abondamment diffusées auprès des astronomes professionnels ou amateurs. Pour quelle raison ? Tout d'abord, l'observateur a souvent besoin d'une confirmation ou d'une simple position approchée. Il est alors simple d'ouvrir un livre et de lire directement une valeur tabulée. On y trouve :
- les heures de lever et de coucher du Soleil et de la Lune (et aussi des planètes principales) ;
- les positions des corps du système solaire et des étoiles brillantes pour un observateur terrestre ;
- les éphémérides pour les observations physiques de ces corps.
Ces éphémérides sont en général de faible précision et des valeurs tabulées sont suffisantes.
Il faut également citer des éphémérides plus spécialisées dans lesquelles les positions des corps célestes sont données dans un but utilitaire : les éphémérides nautiques françaises et le Nautical Almanac anglo-américain sont publiées pour permettre aux marins de faire le point en mer et sont là pour suppléer une défaillance du système GPS. L'éphéméride imprimée garde ici toute son utilité.
Toutes les éphémérides imprimées ne fournissent pas toujours des données tabulées. Elles peuvent donner des représentations graphiques (pour les satellites de Jupiter) ou des coefficients pour polynômes, dans le cas des éphémérides de haute précision, qui nécessitent alors l'emploi d'une calculatrice de poche ou d'un micro ordinateur. C'est le cas de la Connaissance des temps depuis 1979 qui est alors utilisée pour la programmation manuelle des télescopes ou plus simplement pour les tests et les contrôles de programmation plus complexe.
On trouvera ci-dessous la liste des principales éphémérides imprimées publiées actuellement :
- par l'Institut de mécanique céleste et de calcul des éphémérides/Bureau des longitudes :
Guide des données astronomiques
Connaissance des Temps,
Ephémérides nautiques
- par la Société Astronomique de France,
Ephémérides astronomiques
- par le H.M. Nautical Almanac Office de l'ex-Royal Greenwich Observatory (Grande-Bretagne) aujourd'hui au Rutherford Appleton Laboratory et l'USNO (USA) :
Astronomical Ephemerides,
Nautical Almanac ;
- par l'Institut d'astronomie appliquée de Saint-Pétersbourg (Russie) :
Ephémérides des petites planètes ;
- par l'Astronomisches Rechen Institute d'Heidelberg (Allemagne) :
Apparent Places of Fundamental Stars.
Où trouver des éphémérides sur Internet ?
On trouve sur internet de nombreux sites fournissant des éphémérides. Là encore, la précision des positions calculées n'est fournie que sur les sites professionnels. Les données disponibles sont riches et abondantes. Les interfaces interactives sont en général faciles d'utilisation. Attention à l'interprétation des données obtenues !
- serveur de l'Institut de mécanique céleste et de calcul des éphémérides/Bureau des longitudes (Paris, France) http://www.imcce.fr/
- serveur du Jet Propulsion Laboratory (Pasadena, Californie, USA) : http://ssd.jpl.nasa.gov/
- serveur de l'U.S. Naval Observatory (Washington, D.C., USA) : http://aa.usno.navy.mil/
- serveur du H.M. Nautical Almanac Office de l'ex-Royal Greenwich Observatory (Grande-Bretagne) aujourd'hui au Rutherford Appleton Laboratory (Oxford, Grande-Bretagne) : http://www.ast.cam.ac.uk/
- serveur du Minor Planet Center (Cambridge, Massachussets, USA) : (éphémérides d'astéroïdes et de comètes exclusivement) http://minorplanetcenter.net/
Comment faire ses propres éphémérides ?
Fabriquer ses propres éphémérides pour quelques corps du système solaire est un exercice très formateur. Pour cela, il faut consulter les explications de base nécessaires, soit sur les sites Internet fournissant des éphémérides, qui fournissent aussi souvent des outils pour fabriquer soi-même des éphémérides (par exemple pour étendre l'intervalle de temps de validité des éphémérides), soit dans des ouvrages spécialisés. Citons :
- Introduction aux éphémérides astronomiques, Bureau des longitudes, Editions de Physique, avenue du Hoggar, ZA de Courtabœuf, BP 112, F-91944 Les Ulis Cedex, France (en français)
- Explanatory Supplement to the Astronomical Ephemeris, U.S. Naval Observatory/Rutherford Appleton Laboratory (en anglais)
Réponses aux QCM
pages_repere-locaux/utilisation-simulations.html
QCM
'Systèmes de coordonnées'
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 1)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 2)
- Question 5
Aide :
Commencer par chercher la valeur de la déclinaison pour laquelle la hauteur est maximum à l'aide de la première simulation, en prenant en compte la réponse à la question précédente. Vérifier qu'un changement d'ascension droite ne modifie pas le résultat.
Aide :
A partir de la déclinaison, on peut obtenir l'ascension droite correspondante à l'aide de la deuxième simulation.
Solution : réponse 1)
- Question 6
Solution : réponse 2)
- Question 7
Solution : réponse 3)
- Question 8
Solution : réponse 3)
pages_applications/mctc-qcm-reperage.html
QCM
'QCM sur le repérage d'un astre'
- Question 1
Solution : réponse 2)
(
Les deux dernières réponses sont bonnes
)
Solution : réponse 3)
(
Les deux dernières réponses sont bonnes
)
- Question 2
Solution : réponse 1)
(
oui, l'angle horaire se compte à partir de la direction du Sud dans le repère équatorial local
)
- Question 3
Solution : réponse 3)
(
oui, c'est le moyen de trouver l'origine des ascensions droites dans le ciel : le temps sidéral n'est pas un temps mais un angle.
)
- Question 4
Solution : réponse 2)
- Question 5
Solution : réponse 2)
(
oui pour les astronomes (mais les géomètres mesurent les azimuts à partir du Nord)
)
- Question 6
Solution : réponse 1)
(
Avec un instrument méridien, l'angle horaire est nul: Le temps sidéral local est égal à l'ascension droite au moment du passage au méridien.
)
Solution : réponse 2)
(
Avec un instrument méridien, l'angle horaire est nul. L'instrument méridien observe exclusivement vers le Sud
)
pages_heliocentrisme/mctc-qcm-kepler.html
QCM
- Question 1
Solution : réponse 2)
(
oui, les instruments de mesure ne permettaient pas de détecter un mouvement de la Terre
)
Solution : réponse 3)
(
oui, le géocentrisme de Ptolémée permettait de prévoir la plupart des phénomènes célestes
)
- Question 2
Solution : réponse 2)
(
oui, sans l'ellipticité des orbites des planètes, l'héliocentrisme ne fonctionne pas bien
)
Solution : réponse 3)
(
oui, mais seulement par son utilisation de la lunette, parce que ce sont surtout les lois de Kepler qui ont bouleversé notre perception du système solaire
)
pages_distances-systeme/mctc-qcm-distances.html
QCM
- Question 1
Solution : réponse 1)
(
c'est suffisant mais ce n'est pas nécessaire...
)
Solution : réponse 3)
(
oui, la troisième loi de Kepler permet de calculer toutes les autres distances
)
- Question 2
Solution : réponse 2)
(
oui, c'est la distance Terre-Soleil
)
- Question 3
Solution : réponse 1)
(
oui, plus il est près de la Terre, plus sa direction dans le ciel change quand l'observateur se déplace
)
pages_dynamique-systeme/mctc-qcm-trajectoire.html
QCM
- Question 1
Solution : réponse 1)
(
L'ellipse est la solution du problème à deux corps, Terre+masse, mais en première approximation, c'est une parabole.
)
Solution : réponse 3)
(
L'ellipse est la solution du problème à deux corps Terre+masse, mais en première approximation, c'est une parabole.
)
- Question 2
Solution : réponse 3)
(
oui, il y a plus de deux corps dans le système solaire et les trajectoires sont très complexes bien que proches d'ellipses en déformation constante
)
- Question 3
Solution : réponse 3)
(
oui, à cette altitude la vitesse d'un satellite est la même que celle de la Terre autour de son axe et le satellite surplombe toujours la même région terrestre
)
pages_mouvements-planetes/mctc-qcm-planete.html
QCM
- Question 1
Solution : réponse 1)
(
oui, les perturbations sur Uranus étaient maximales à cette date, il y avait donc une planète supplémentaire pas bien loin
)
- Question 2
Solution : réponse 1)
(
(oui, c'est tout à fait par hasard que Tombaugh a découvert Pluton
)
- Question 3
Solution : réponse 1)
(
L'inclinaison de l'axe de la Terre et l'excentricité de l'orbite de la Terre ont une influence sur le climat. Dans le passé, une excentricité nulle a causé un age glaciaire.
)
Solution : réponse 3)
(
L'inclinaison de l'axe de la Terre et l'excentricité de l'orbite de la Terre ont une influence sur le climat de la Terre.
)
pages_relativite-einstein/mctc-qcm-relativite.html
QCM
- Question 1
Solution : réponse 3)
(
oui, la relativité générale explique que la masse du Soleil déforme l'espace et modifie le mouvement de Mercure par rapport à un mouvement newtonien simple
)
Réponses aux exercices
pages_defrepere/mctc-application-sphere.html
Exercice
'La sphère céleste'
pages_defrepere/calculcoordpolaire.html
Exercice
'Calcul de coordonnées polaires'
pages_defrepere/calculpolaire3d.html
Exercice
'Calcul de coordonnées polaires'
pages_defrepere/conversion.html
Exercice
'Conversion des unités'
pages_defrepere/mctc-exo-repere-equatorial.html
Exercice
'Le repère écliptique'
- Question 1
Aide :
Dans l'hémisphère nord le Soleil culmine dans le ciel le jour du solstice d'été et il est au plus bas le jour du solstice d'hiver.
Ne pas oublier que le Soleil est toujours dans l'écliptique été comme hiver et que l'écliptique est toujours visible dans le ciel jour et nuit.
pages_defrepere/relation-ecliptique-equatoriale.html
Exercice
'Calcul des coordonnées équatoriales du Soleil'
pages_defrepere/calcul-latitude-geocentrique.html
Exercice
'Calcul de la latitude géocentrique de Paris'
pages_defrepere/mctc-exo-temps-sideral.html
Exercice
'Le temps sidéral'
pages_defrepere/variation-temps-sideral.html
Exercice
'Calcul du temps sidéral local en un lieu donné'
pages_defrepere/utilisation-simulations.html
Exercice
'Visibilité des étoiles'
- Question 1
Aide :
Attention au décalage horaire !
Pour simplifier, on pourra prendre minuit heure locale sans tenir compte des différences heures d'été / heures d'hiver.
Aide :
Par convention, la longitude est positive vers l'Est. Donc 140° E = +140°.
- Question 2
- Question 3
pages_defrepere/exercice-meridien.html
Exercice
'Passage du Soleil au méridien'
pages_defrepere/mctc-exo-declinaison.html
Exercice
'La déclinaison d'une étoile au zénith'
pages_mesure-distances/mctc-exo-triangulation.html
Exercice
'Calcul d'une distance par triangulation'
- Question 1
Aide :
Pour calculer la distance CH, il suffit de résoudre le triangle ABC connaissant les deux angles en A et B et la base AB. On applique une des relations entre angles et côtés dans un triangle.
Aide :
Rappel : dans un triangle quelconque ABC, on a la relation :
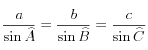
pages_mesure-distances/mctc-calcul-triangulation.html
Exercice
'Calcul d'une distance par triangulation'
- Question 1
Aide :
La distance Alexandrie-Syène est de 5000 stades soit 800 km. L'angle zénith-observateur-Soleil mesuré depuis Alexandrie est de 7°.
Aide :
Le diamètre apparent du soleil est 0,5°.
pages_mesure-distances/mctc-distances-systeme-solaire.html
Exercice
'Les distances dans le système solaire'
pages_kepler/mctc-demi-grand-axe.html
Exercice
'Calcul du demi grand axe d'Uranus'
pages_kepler/mctc-distance-terre-saturne.html
Exercice
'Distance minimale Terre-Saturne'
- Question 1
Aide :
1 unité astronomique égale (environ): 150 millions de km,
c'est le demi grand axe de la Terre
sa période de révolution est un an
Aide :
Calculer tout d'abord le demi-grand axe de Saturne
 Introduction
Introduction Prérequis
Prérequis et
et  : Niveau Physique Licence scientifique
: Niveau Physique Licence scientifique


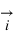 , ce vecteur porte donc le nom de vecteur unitaire.
, ce vecteur porte donc le nom de vecteur unitaire.
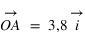 et que
et que 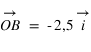 .
.
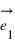 et
et 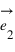 ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
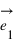 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 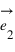 ; et sur l'axe portant le vecteur
; et sur l'axe portant le vecteur 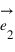 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 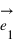 . Les coordonnées
. Les coordonnées 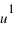 et
et 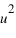 du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire : 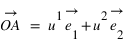 , les coordonnées
, les coordonnées 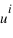 sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).





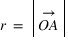 du point A au centre O du repère et l’angle entre la direction OA et l’un des axes. L'angle est compté positivement dans le sens direct (sens inverse des aiguilles d'une montre), souvent à partir de l'axe Ox
du point A au centre O du repère et l’angle entre la direction OA et l’un des axes. L'angle est compté positivement dans le sens direct (sens inverse des aiguilles d'une montre), souvent à partir de l'axe Ox
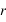 ,
,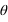 ) par les relations mathématiques suivantes :
) par les relations mathématiques suivantes :
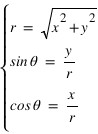 Les deux dernières relations peuvent être remplacées par
Les deux dernières relations peuvent être remplacées par 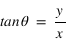 , mais l'on doit alors choisir le bon angle
, mais l'on doit alors choisir le bon angle 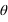 et fonction des signes de
et fonction des signes de 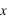 et de
et de 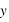
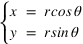
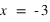 et
et 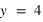 .
.

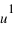 ,
,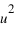 et
et 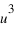 du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire : 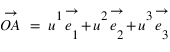 , les coordonnées
, les coordonnées 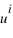 sont appelées coordonnées contravariantes du vecteur
sont appelées coordonnées contravariantes du vecteur 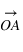 (ou projections parallèles). Elles sont souvent notées (x,y,z).
(ou projections parallèles). Elles sont souvent notées (x,y,z).
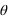 ,
,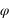 ) et une distance
) et une distance 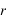 . L’angle
. L’angle 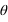 est l’angle entre la projection OA’ de OA dans le plan (Oxy) et l’axe Ox. L’angle
est l’angle entre la projection OA’ de OA dans le plan (Oxy) et l’axe Ox. L’angle 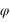 est l’angle entre OA et sa projection OA’. r est la distance entre l’origine O est le point A.
est l’angle entre OA et sa projection OA’. r est la distance entre l’origine O est le point A.
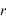 ,
,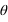 ,
,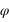 ) aux coordonnées cartésiennes (x,y,z) grâce aux relations suivantes :
) aux coordonnées cartésiennes (x,y,z) grâce aux relations suivantes :
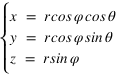
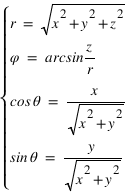
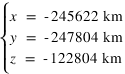 Calculer les coordonnées polaires (
Calculer les coordonnées polaires (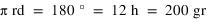
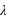 ) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée
) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée 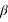 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.

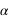 ) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée
) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée 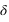 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée 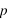 ).
).



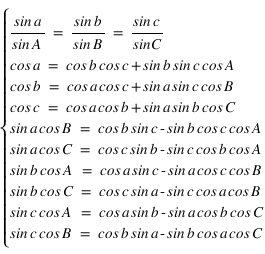

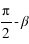 ,
,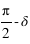 ,
,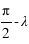 ,
,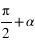 .
.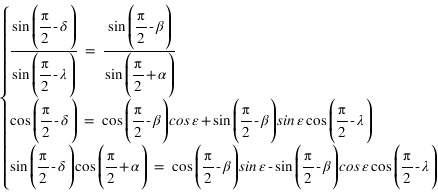
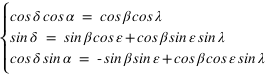
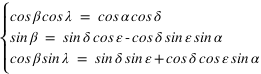
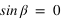 et que
et que 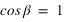 . Le système (1) est donc simplifié.
. Le système (1) est donc simplifié.
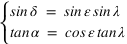 .
Faites attention aux unités, la calculatrice en ligne utilise des radians !
.
Faites attention aux unités, la calculatrice en ligne utilise des radians !


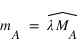 , sa longitude écliptique étant
, sa longitude écliptique étant 


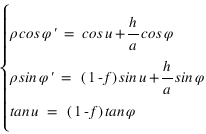
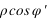 et
et 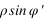 est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
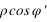 et
et 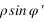 .
.


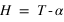
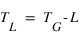
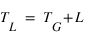
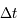 et la variation
et la variation 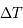 du temps sidéral :
du temps sidéral :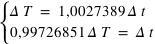


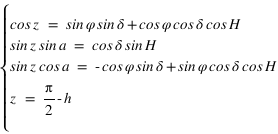
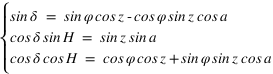




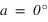 et
et 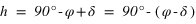 équation (1)
équation (1)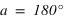 et
et 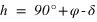 équation (2)
équation (2)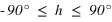 .
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si
.
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si 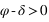 donc si
donc si 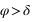 . Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si
. Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si 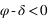 donc si
donc si 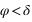 . Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors
. Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors 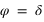 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.

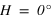 ) les équations de transformations de coordonnées donnent :
) les équations de transformations de coordonnées donnent :
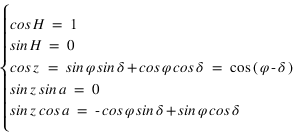
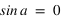 alors
alors 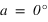 ou
ou 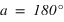 , si
, si 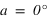 alors
alors 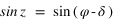 et si
et si 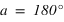 alors
alors 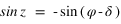 .
.
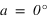 et
et 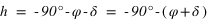 équation (3)
équation (3)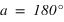 et
et 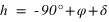 équation (4)
équation (4)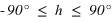 . On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si
. On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si 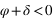 donc si
donc si 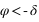 . Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si
. Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si 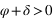 donc si
donc si 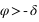 . Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors
. Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors 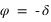 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.

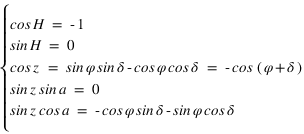
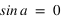 alors
alors 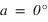 ou
ou 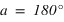 . Si
. Si 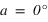 alors
alors 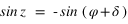 et si
et si 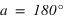 alors
alors 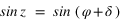 .
.
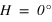
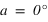
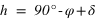
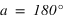
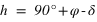
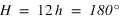
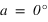
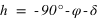
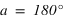
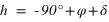
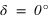 ) et le méridien supérieur => équation (1) ou (2) avec h positif.
) et le méridien supérieur => équation (1) ou (2) avec h positif.
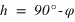 (colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
(colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
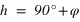 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
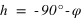 et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
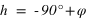 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
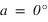 et
et 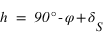 équation (1)
équation (1)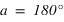 et
et 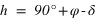 équation (2)
équation (2)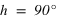 , alors a n’est plus défini, et :
, alors a n’est plus défini, et : 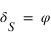
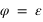 la solution est
la solution est 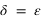 , donc le Soleil passe au zénith le jour du solstice d’été de juin. Un raisonnement identique pour le tropique du Capricorne montre que le Soleil passe au zénith uniquement le jour du solstice d’été de l’hémisphère sud. Sur l’équateur
, donc le Soleil passe au zénith le jour du solstice d’été de juin. Un raisonnement identique pour le tropique du Capricorne montre que le Soleil passe au zénith uniquement le jour du solstice d’été de l’hémisphère sud. Sur l’équateur 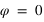 le Soleil passe au zénith deux fois par an lorsque sa déclinaison est nulle, c’est-à-dire aux équinoxes.
le Soleil passe au zénith deux fois par an lorsque sa déclinaison est nulle, c’est-à-dire aux équinoxes.
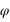 , quelle sera la déclinaison de cette étoile ?
, quelle sera la déclinaison de cette étoile ?

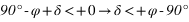
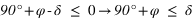
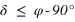 . De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant
. De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 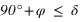 . Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
. Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
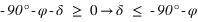
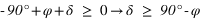
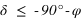 .
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant
.
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant 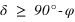 .
.
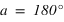 ) donc
) donc 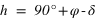 doit être inférieur à 90° donc
doit être inférieur à 90° donc 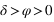 .
.
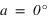 ) donc
) donc 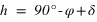 doit être inférieur à 90° donc
doit être inférieur à 90° donc 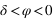 .
.
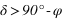 équation (1)
équation (1)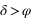 équation (2)
équation (2)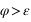 ) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.
) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.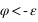 ), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.
), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.


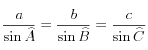

















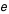 telle que
telle que 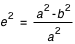 où
où 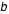 est le demi-petit axe
est le demi-petit axe 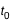 ou l'anomalie moyenne
ou l'anomalie moyenne 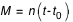 où
où 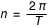 avec
avec 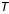 période de révolution définie par la 3ème loi de Kepler (qui dit que
période de révolution définie par la 3ème loi de Kepler (qui dit que 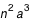 est une constante connue).
est une constante connue).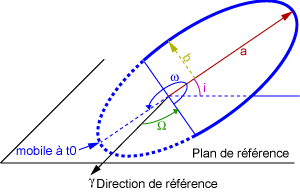

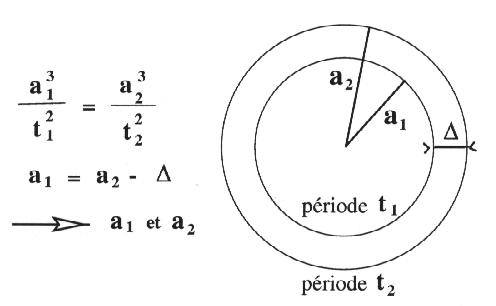


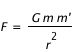 où G est la constante gravitationnelle.
où G est la constante gravitationnelle.



![F_j = \[\sum_{i=1 (i\neq j)}^N\]\frac{k~m_i~m_j~P_i~P_j}{\mid P_i~P_j\mid ^3}](../pages_mecanique-celeste/equations_dynamique-systeme/equation1.png)
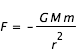











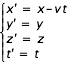
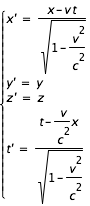
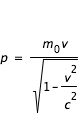
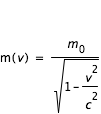
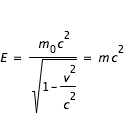
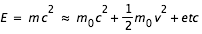
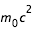





















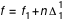
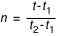 et
et 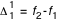

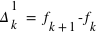
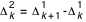 {k=0,1,2,...}
{k=0,1,2,...}
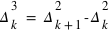
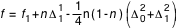
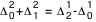



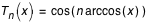
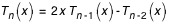 avec
avec 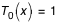 et
et 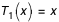
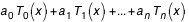

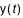 par la formule :
par la formule :
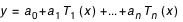
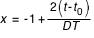
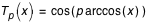 ;
; 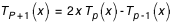 Avec :
Avec : 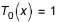 ;
; 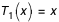
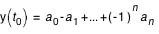
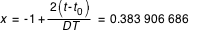
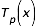 sont calculés par la relation (3) :
sont calculés par la relation (3) :
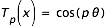 où
où 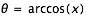
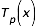 sont calculés par la relation de récurrence (4) :
sont calculés par la relation de récurrence (4) :
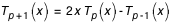
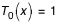 ;
; 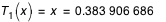
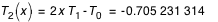 ,
,
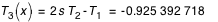 , etc
, etc
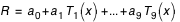 ,
,

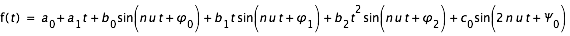 .
.
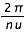 est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les
est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les 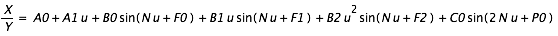 (5),
(5),
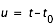 (u est compté en jours).
(u est compté en jours).
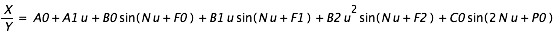 ,
,

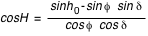 où
où
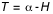 ;
;
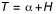 .
.
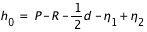 ,
,
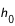 l'angle
l'angle 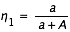 , où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
, où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
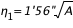 ,
,
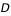 situées à la distance
situées à la distance 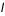 de l'observateur, on ajoutera à
de l'observateur, on ajoutera à 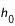 l'angle
l'angle 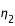 tel que :
tel que :
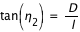 .
.



