Au vu de la difficulté d'observer directement une exoplanète, d'autres méthodes peuvent être envisagées, qui vont chercher à observer le mouvement induit par la planète sur son étoile.
Mouvement d'une étoile dû à une planète
On présente souvent les lois de Kepler en disant que l'orbite d'une planète est une ellipse dont son étoile occupe l'un des foyers. Mais l'on pourrait tout aussi bien dire que le couple étoile-planète tourne autour du centre de gravité de ce système. Certes, la masse de l'étoile étant beaucoup plus grande que celle de la planète, ce centre de gravité sera très proche du centre de l'étoile, mais pas tout à fait. Et ce "pas tout à fait" a ici une importance cruciale, car il fait que l'étoile a elle aussi un mouvement, décrivant une petite orbite autour du centre de gravité de son système.
Ainsi, pour une planète de masse Mpl dont l'orbite autour de son étoile de masse M* est une ellipse de demi-grand axe a, le mouvement de l'étoile autour du centre de gravité du système est une ellipse de demi-grand axe a* :
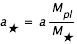
Dans le cas simplifié où la planète est sur orbite circulaire, 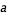 est constant et il en est donc de même de a* de sorte que l'étoile suit une trajectoire circulaire autour du centre de masse.
est constant et il en est donc de même de a* de sorte que l'étoile suit une trajectoire circulaire autour du centre de masse.
mouvement orbital d'un couple étoile-planète

Mouvements respectifs d'une étoile et d'une planète moins massive autour du centre de gravité du système étoile-planète
Crédit :
(Rtn20)
La période orbitale de l'étoile sera la même que celle de la planète et est donnée par la 3ème loi de Kepler :
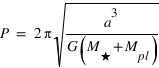
où 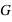 est la constante de la gravitation,
est la constante de la gravitation, 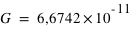
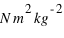
Du fait de la faible masse de la planète, le mouvement de l'étoile est très limité, mais il peut cependant s'observer, et ce de trois manières différentes :
- vitesses radiales
- astrométrie
- chronométrage
Cette méthode, même si elle n'est pas la plus simple dans son principe, est la première à avoir permis la découverte d'une exoplanète autour d'une étoile de type solaire en 1995. Elle a été pendant plusieurs années la méthode par laquelle la quasi-totalité des exoplanètes était trouvée. Même si aujourd'hui beaucoup d'autres méthodes moissonnent avec succès de nouvelles planètes, il n'en reste pas moins que plus de 2/3 des exoplanètes découvertes à ce jour l'ont été par la méthode des vitesses radiales.
Principe de la méthode
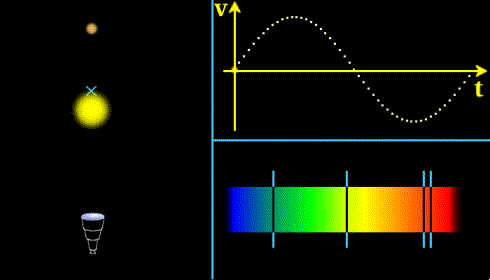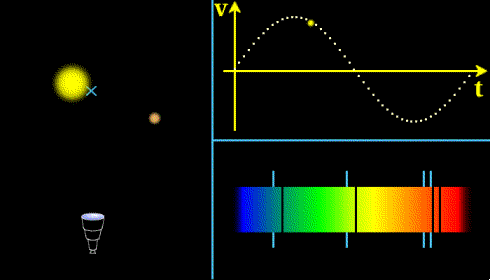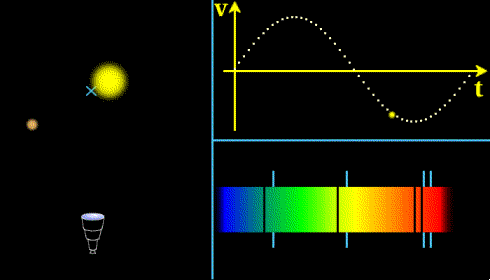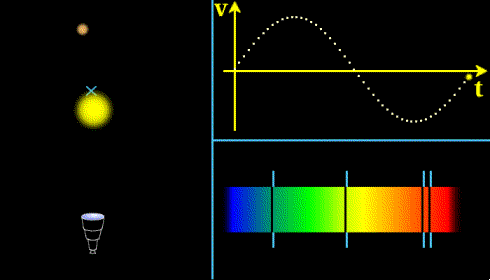
Effet Doppler sur la lumière provenant d'une étoile perturbée par une planète. La lumière est décalée vers le bleu (courtes longueurs d'onde) lorsque l'étoile se rapproche de nous, et vers le rouge quand elle s'éloigne. La courbe en haut à droite donne la courbe de vitesse radiale de l'étoile que l'on peut déduire de son décalage Doppler.
Crédit :
Observatoire de Paris/ASM Emmanuel Pécontal
Le principe de cette méthode est de détecter le mouvement d'une étoile en observant l'effet Doppler sur la lumière qui nous en provient. Quand l'étoile a un mouvement qui la fait se rapprocher de nous, sa lumière est décalée vers le bleu, alors qu'elle est décalée vers le rouge quand elle s'éloigne. L'amplitude de ces décalages est proportionnelle à la vitesse de l'étoile.
Dans le cas simplifié où l'orbite de l'étoile (due à une planète) est parfaitement circulaire, la vitesse VR à laquelle elle s'éloigne ou se rapproche de nous varie en fonction du temps suivant :
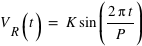
où K est l'amplitude de la variation de 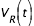 , donnée par :
, donnée par :
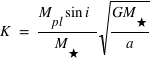
où i est l'angle entre la ligne de visée de l'observateur et la perpendiculaire au plan de l'orbite de la planète. L'effet Doppler est maximum quand cet angle est égal à 90°, c'est-à-dire quand on regarde l'orbite "par la tranche". Quand i est nul, la vitesse de l'étoile n'a pas de composante radiale. Dans ce cas, même si une planète est présente, cette méthode ne permet pas de la détecter.
L'amplitude de l'effet Doppler induit par le mouvement de l'étoile est de l'ordre de K/c, où c est la vitesse de la lumière, c'est-à-dire de quelques m/s (la vitesse d'un homme qui court !) divisés par 300 000 km/s ! (voir ce petit exercice, pour calculer cet effet pour la Terre et pour Jupiter). Il s'agit donc de mesurer des effets extrêmements fins. A l'heure actuelle, on peut détecter des vitesses radiales de l'ordre de ∼0.5 m/s, c'est-à-dire qu'une "exo Terre" est presque à notre portée.
On voit que cette méthode favorise la détection de planètes massives et proches de leur étoile, car l'amplitude K est directement proportionnelle à Mpl et inversement proportionnelle à 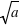 . Et de fait, les premières planètes détectées par effet Doppler étaient des "Jupiter chaud", c'est-à-dire des planètes de la masse de Jupiter mais situées extrêmement près de leur étoile (plus près que Mercure). Le plus célèbre de ces Jupiter chaud est la planète 51 Pégase b, la toute première à avoir été détectée.
. Et de fait, les premières planètes détectées par effet Doppler étaient des "Jupiter chaud", c'est-à-dire des planètes de la masse de Jupiter mais situées extrêmement près de leur étoile (plus près que Mercure). Le plus célèbre de ces Jupiter chaud est la planète 51 Pégase b, la toute première à avoir été détectée.
Courbe de vitesse de l'étoile 51 Pegase (1995)
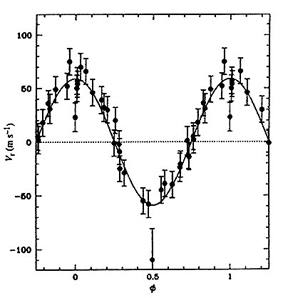
Cette courbe est historique, car elle correspond à la première détection d'une exoplanète autour d'une étoile de type solaire. Cette observation a été réalisée à l'Observatoire de Haute-Provence, par Michel Mayor et Didier Queloz, de l'Observatoire de Genève.
Crédit :
(M.Mayor & D.Queloz)
Depuis 1995, quantité d'autres exoplanètes ont été découvertes par cette méthode. Et si initiallement la plupart d'entre elles étaient des Jupiter chaud (car ce sont les plus faciles à détecter), celles découvertes aujourd'hui sont de tout type : "Jupiter froid", "Neptune-chaud", "super-Terre", etc. Voir l'Encyclopédie des planètes extrasolaires pour une liste actualisée de toutes les exoplanètes découvertes par effet Doppler.
Astrométrie
L'astrométrie consiste à mesurer un autre effet induit par la planète sur son étoile, non plus ses variations de vitesse (comme pour la méthode Doppler), mais les variations de sa position apparente sur le fond du ciel par rapport aux autres étoiles.
Mouvement astrométrique du Soleil vu à 10 parsecs
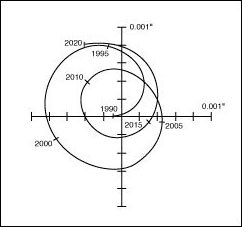
Mouvement de notre étoile induit par son cortège de planètes, vu depuis une distance de 10 pc.
Cette méthode relève vraiment du défi, car par exemple, le mouvement induit par Jupiter sur le Soleil vu depuis l'étoile la plus proche (4 années-lumière) n'est que de 0.004" (environ 0.000001 degré !), soit beaucoup moins que la résolution des télescopes au sol les plus performants. La seule solution est de réaliser des observations ultra-précises sur des intervales de temps très longs, ou bien d'utiliser des télescopes spatiaux.
Cette méthode n'a, pour l'instant, pas encore porté ses fruits : elle a permis l'observation de planètes déjà détectées par d'autres méthodes mais encore pas la découverte de nouveaux objets. Cela devrait changer avec l'observatoire spatial européen GAIA.
Chronométrage
On peut aussi mesurer une autre conséquence indirecte de la présence d'une planète : la variation de la distance entre l'étoile et l'observateur. La meilleure méthode pour mesurer cette variation est de mesurer la variation 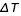 de temps que met la lumière à nous parvenir de l'étoile. A chaque instant cette variation est donnée par :
de temps que met la lumière à nous parvenir de l'étoile. A chaque instant cette variation est donnée par :
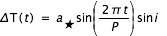
Pour mesurer cette variation le plus simple est de mesurer les variations de temps d'arrivée d'un signal périodique.  est alors le retard ou l'avance de l'instant d'arrivée du signal par rapport à un instant "nominal" (sans perturbation). Tout le problème est d'avoir à sa dispostion un système stellaire possédant un tel signal périodique. On connaît 2 types de systèmes possédants de tels signaux :
est alors le retard ou l'avance de l'instant d'arrivée du signal par rapport à un instant "nominal" (sans perturbation). Tout le problème est d'avoir à sa dispostion un système stellaire possédant un tel signal périodique. On connaît 2 types de systèmes possédants de tels signaux :
- Les pulsars
- Les étoiles binaires à éclipse, dont la luminosité chute à intervalle de temps régulier
C'est la méthode qui a actuellement le "vent en poupe". Son principe est simple : si on a la chance d'observer un système étoile-planète exactement "par la tranche", alors on peut assister à un transit de la planète devant son étoile. Lors de ce transit une petite fraction de la lumière stellaire est cachée par la planète et donc le signal lumineux en provenance de l'étoile chute légèrement le temps du transit (voir Figure).
Simulation (animation)
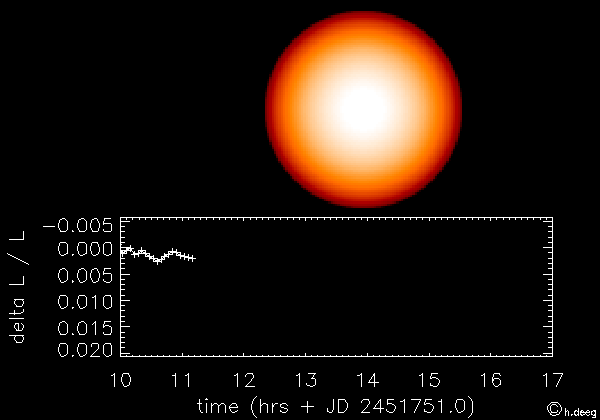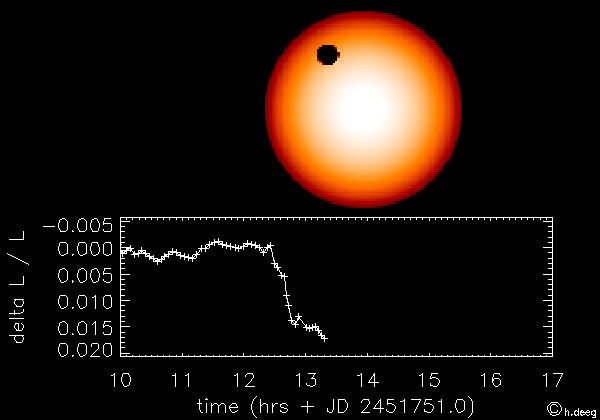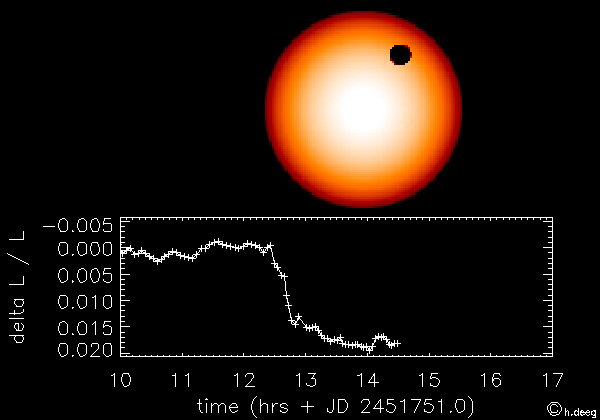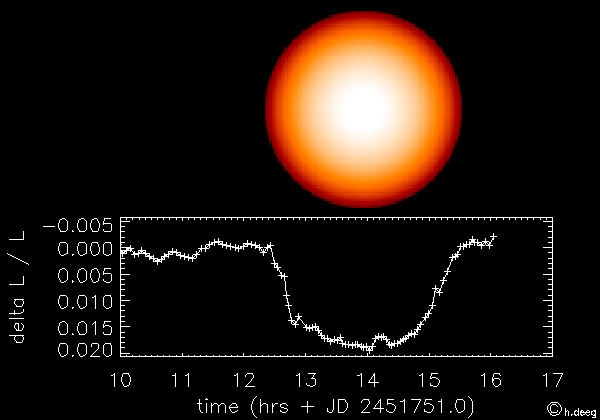
Crédit :
Hans Deeg (Instituto de Astrofisica de Canarias)
La chute de luminosité est de l'ordre de (Rpl/R*)2, où Rpl est le rayon de la planète et R* celui de l'étoile. L'effet est certes petit, mais il est bien plus important que le rapport de luminosité directe entre la planète et l'étoile, qui est lui de l'ordre de (Rpl/d)2, où d est cette fois-ci la distance de la planète à l'étoile (voir exercice page suivante).
Exemple de courbe de lumière
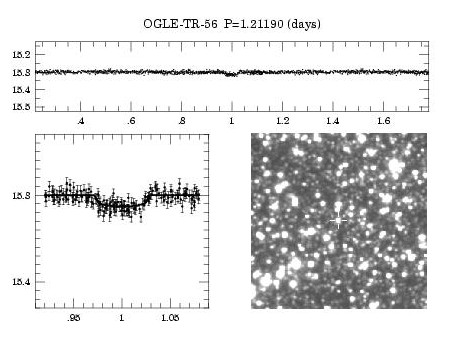
courbe de lumière autour de l'étoile OGLE-TR-56
Crédit :
Groupe Ogle
La principale difficulté de cette méthode n'est pas tant l'amplitude de l'effet à mesurer que le fait qu'il faut une situation très favorable et a priori peu probable pour voir un transit, à savoir être exactement aligné avec l'orbite planétaire (voir exercice page suivante). De ce fait, la solution est de réaliser un très grand nombre d'observations d'étoiles, pour être sûr d'avoir au moins une chance d'être dans une configuration favorable.
Le premier transit planétaire a été observé en 1999, et depuis lors, plus de 2000 planètes ont été observées par cette méthode. Le rythme de détection s'est très fortement accéléré ces dernières années, avec l'arrivée du télescope spatial français COROT et du télescope KEPLER de la NASA, tous deux dédiés à ce type d'observations.
C'est une application de la théorie d'Einstein de la gravitation. Celle-ci prédit que lorsqu'un corps de masse M (déflecteur) est à une distance b projetée sur le ciel ("paramètre d'impact") de la ligne de visée d'une source lointaine, l'éclat apparent de cette dernière est amplifié par un facteur 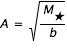 . Lorsque la source et le déflecteur se déplacent l'un par rapport à l'autre sur le plan du ciel, le paramètre d'impact b varie au cours du temps. Il en est donc de même du facteur d'amplification qui devient une fonction du temps A(t).
. Lorsque la source et le déflecteur se déplacent l'un par rapport à l'autre sur le plan du ciel, le paramètre d'impact b varie au cours du temps. Il en est donc de même du facteur d'amplification qui devient une fonction du temps A(t).
Principe d'une détection par lentille gravitationnelle
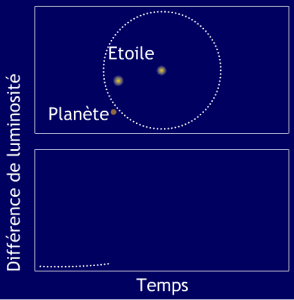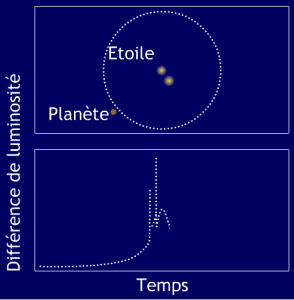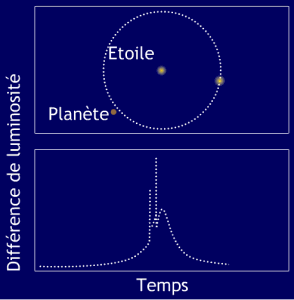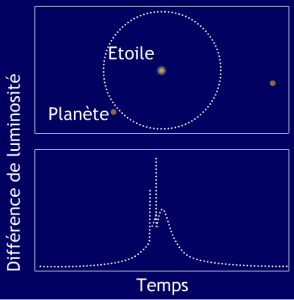
Saut de luminosité dû à un phénomène de lentille gravitationnelle. Une étoile lointaine passe exactement derrière une autre étoile autour de laquelle orbite une planète. L'étoile proche focalise la lumière de l'étoile lointaine, ce qui crée une augmentation de la luminosité. La planète focalise aussi la lumière de l'étoile lointaine, ce qui crée les deux pics de luminosité visibles avant le maximum.
Crédit :
Observatoire de Paris / UFE
La probabilité d'observer un tel évènement est très faible. De ce fait, cette méthode de l'extrême nécessite d'observer un large champ stellaire pendant très longtemps pour avoir une chance d'assister à un phénomène de lentille.
Cette méthode de l'extrême a porté ses fruits : plus de 80 planètes ont été ainsi détectées à ce jour.
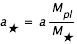
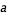 est constant et il en est donc de même de a* de sorte que l'étoile suit une trajectoire circulaire autour du centre de masse.
est constant et il en est donc de même de a* de sorte que l'étoile suit une trajectoire circulaire autour du centre de masse.

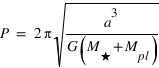
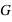 est la constante de la gravitation,
est la constante de la gravitation, 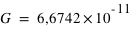
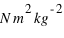

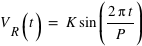
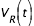 , donnée par :
, donnée par :
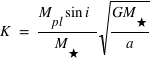
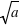 . Et de fait, les premières planètes détectées par effet Doppler étaient des "Jupiter chaud", c'est-à-dire des planètes de la masse de Jupiter mais situées extrêmement près de leur étoile (plus près que Mercure). Le plus célèbre de ces Jupiter chaud est la planète 51 Pégase b, la toute première à avoir été détectée.
. Et de fait, les premières planètes détectées par effet Doppler étaient des "Jupiter chaud", c'est-à-dire des planètes de la masse de Jupiter mais situées extrêmement près de leur étoile (plus près que Mercure). Le plus célèbre de ces Jupiter chaud est la planète 51 Pégase b, la toute première à avoir été détectée.

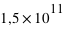 m, et que la masse du Soleil est de
m, et que la masse du Soleil est de 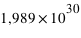 kg, quelle est l'amplitude K de variation de la vitesse d'une étoile de 1 masse solaire pour :
kg, quelle est l'amplitude K de variation de la vitesse d'une étoile de 1 masse solaire pour :
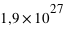 kg) à 5 UA sur une orbite inclinée de 60 degrés.
kg) à 5 UA sur une orbite inclinée de 60 degrés. 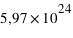 kg) à 1 UA sur une orbite inclinée de 90 degrés.
kg) à 1 UA sur une orbite inclinée de 90 degrés.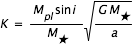

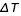 de temps que met la lumière à nous parvenir de l'étoile. A chaque instant cette variation est donnée par :
de temps que met la lumière à nous parvenir de l'étoile. A chaque instant cette variation est donnée par :
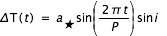
 est alors le retard ou l'avance de l'instant d'arrivée du signal par rapport à un instant "nominal" (sans perturbation). Tout le problème est d'avoir à sa dispostion un système stellaire possédant un tel signal périodique. On connaît 2 types de systèmes possédants de tels signaux :
est alors le retard ou l'avance de l'instant d'arrivée du signal par rapport à un instant "nominal" (sans perturbation). Tout le problème est d'avoir à sa dispostion un système stellaire possédant un tel signal périodique. On connaît 2 types de systèmes possédants de tels signaux :


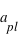 (rayon de l’orbite de la planète), et où le côté opposé mesure
(rayon de l’orbite de la planète), et où le côté opposé mesure 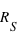 (rayon du Soleil). On a alors :
(rayon du Soleil). On a alors :
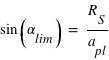 où
où 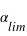 est l’angle entre la ligne de visée et le plan de l’orbite de la planète autour du Soleil.
est l’angle entre la ligne de visée et le plan de l’orbite de la planète autour du Soleil.
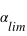 est très petit,
est très petit, 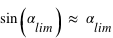 , où l'angle
, où l'angle 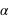 est exprimé en radians.
est exprimé en radians.
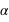 , est plus petit que
, est plus petit que 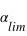 , les transits sont détectables de RX92.
, les transits sont détectables de RX92.
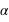 peut prendre toutes les valeurs entre 0 et
peut prendre toutes les valeurs entre 0 et 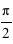 radians, mais seules les valeurs entre 0 et
radians, mais seules les valeurs entre 0 et 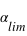 donnent un transit détectable. La probabilité de transits détectables est donc égale au rapport
donnent un transit détectable. La probabilité de transits détectables est donc égale au rapport 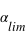 /
/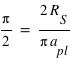
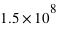 km. L'orbite de Jupiter a un rayon de
km. L'orbite de Jupiter a un rayon de 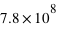 km. le Soleil a un rayon de
km. le Soleil a un rayon de 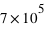 km.
km.
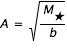 . Lorsque la source et le déflecteur se déplacent l'un par rapport à l'autre sur le plan du ciel, le paramètre d'impact b varie au cours du temps. Il en est donc de même du facteur d'amplification qui devient une fonction du temps A(t).
. Lorsque la source et le déflecteur se déplacent l'un par rapport à l'autre sur le plan du ciel, le paramètre d'impact b varie au cours du temps. Il en est donc de même du facteur d'amplification qui devient une fonction du temps A(t).
