Exercice : méthode des transits (2)

Question 1)

Vous êtes sur la lointaine planète RX92 et vous cherchez des exoplanètes autour du Soleil par la méthode des transits. On suppose que les planètes sont des points sur le disque du Soleil, c’est-à-dire qu’on ne prend pas en compte leur taille. Nous allons calculer quelle est la probabilité que, vue de RX92, une planète soit détectable par transit, c’est-à-dire qu’elle passe devant le Soleil (figure du haut).

Pour cela, regardons le système vu de côté au moment où la planète est « au milieu du Soleil » (dessin du milieu). La condition pour que le transit soit visible est que, à ce moment-là, le disque de la planète se projette sur le disque du Soleil.

Dans le cas limite, c’est-à-dire quand la planète passe juste « au bord » du Soleil, on a le triangle rectangle de la figure du bas où l’hypoténuse mesure 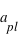(rayon de l’orbite de la planète), et où le côté opposé mesure 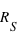(rayon du Soleil). On a alors : 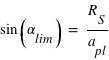où 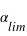est l’angle entre la ligne de visée et le plan de l’orbite de la planète autour du Soleil.

Comme 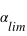est très petit, 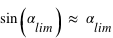, où l'angle 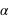est exprimé en radians.

Si, pour une planète donnée du Soleil, l'angle entre le plan de son orbite et la ligne de visée, appelons-le 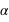, est plus petit que 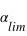, les transits sont détectables de RX92.

L'angle 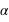peut prendre toutes les valeurs entre 0 et 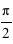radians, mais seules les valeurs entre 0 et 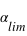donnent un transit détectable. La probabilité de transits détectables est donc égale au rapport /

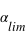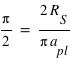
Quelle est la probabilité d'observer les transits de la Terre devant le Soleil ?

Même question pour Jupiter.

Aide