 |  |  |  |  |  |
Des Etoiles aux Planètes Exoplanètes Méthodes de détection des exoplanètesMéthodes dynamiques : principe |
Au vu de la difficulté d'observer directement une exoplanète, d'autres méthodes peuvent être envisagées, qui vont chercher à observer le mouvement induit par la planète sur son étoile.
On présente souvent les lois de Kepler en disant que l'orbite d'une planète est une ellipse dont son étoile occupe l'un des foyers. Mais l'on pourrait tout aussi bien dire que le couple étoile-planète tourne autour du centre de gravité de ce système. Certes, la masse de l'étoile étant beaucoup plus grande que celle de la planète, ce centre de gravité sera très proche du centre de l'étoile, mais pas tout à fait. Et ce "pas tout à fait" a ici une importance cruciale, car il fait que l'étoile a elle aussi un mouvement, décrivant une petite orbite autour du centre de gravité de son système.
Ainsi, pour une planète de masse Mpl dont l'orbite autour de son étoile de masse M* est une ellipse de demi-grand axe a, le mouvement de l'étoile autour du centre de gravité du système est une ellipse de demi-grand axe a* :
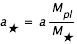
Dans le cas simplifié où la planète est sur orbite circulaire,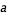 
est constant et il en est donc de même de a* de sorte que l'étoile suit une trajectoire circulaire autour du centre de masse.
La période orbitale de l'étoile sera la même que celle de la planète et est donnée par la 3ème loi de Kepler :
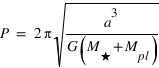
où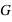 
est la constante de la gravitation,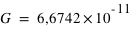 
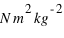
Du fait de la faible masse de la planète, le mouvement de l'étoile est très limité, mais il peut cependant s'observer, et ce de trois manières différentes :
 |  |