Etoiles à neutrons
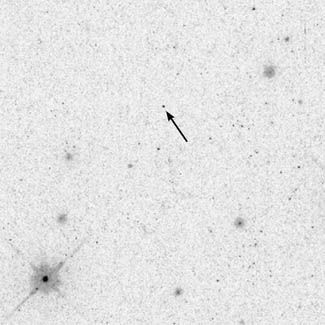
Etoile à neutrons RX J185635-3754. Elle a été découverte d'abord par son émission X, puis identifiée par le télescope Hubble. Sa magnitude apparente visible est de 25. Estimation du diamètre : 28 km ; de la température : 600 000 K.
Crédit :
HST
Etoile à neutrons
Un objet simultanément très chaud (plusieurs centaines de milliers de Kelvin, soit bien plus qu'une étoile de la séquence principale) et très peu lumineux ne peut être, d'après la loi de rayonnement du corps noir, qu'extrêmement petit. C'est ainsi qu'ont été identifiées les étoiles à neutrons, rayonnant l'essentiel de leur énergie dans les domaines X et gamma.
Pulsar

Pulsar du Crabe, résidu de la supernova de 1054.
Crédit :
HST
Pulsars
Un pulsar (de l'anglais pulsating radio source) correspond à une étoile à neutrons dont on observe le rayonnement électromagnétique modulé par la rotation rapide. La rapidité de la période de rotation observée provient du très petit rayon de l'étoile à neutrons.
Le faisceau du pulsar correspond au rayonnement synchrotron des électrons accélérés le long des lignes de champ magnétique. C'est ce phénomène de pulsar qui a conduit à la découverte des premières étoiles à neutrons.
 Objectifs
Objectifs
Décrire simplement cet objet hors du commun qu'est une étoile à neutrons.
Neutron et étoiles à neutron
L'existence des étoiles à neutrons a été supposée dès
l'identification du neutron, comme résidus de supernova.
Bousculade
Au delà de la masse de Chandrasekhar, la pression de Fermi des électrons ne peut plus soutenir l'étoile. La contraction conduit les électrons à flirter intensément avec les protons. L'interaction nucléaire faible est alors sollicitée : elle transforme un proton et un électron en un neutron.
Neutronisation
Néanmoins, la réaction de neutronisation :
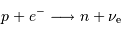
est impossible au repos, car le bilan de masse ne lui est pas favorable. En effet, l'énergie de masse de l'électron (0.5 MeV) apparaît bien inférieure à la différence d'énergie de masse entre proton et neutron (1.3 MeV).
Néanmoins, lorsque les électrons deviennent relativistes, leur énergie totale peut dépasser ce niveau nécessaire de 1.3 MeV (atteint pour une vitesse de 0.92 c). La réaction de neutronisation devient alors possible. C'est cette condition sur la vitesse des électrons qui se traduit par le seuil de masse correspondant à la masse de Chandrasekhar.
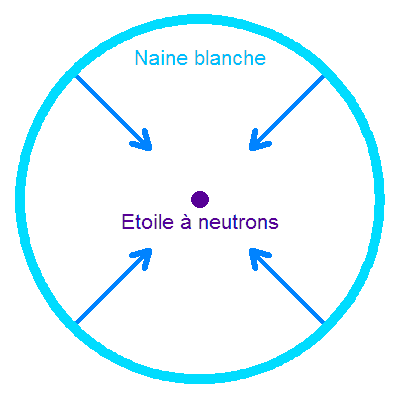
Effondrement d'une naine blanche vers une étoile à neutrons, lorsqu'a lieu la réaction de neutronisation.
Crédit :
ASM
Conséquences
Les neutrons, qui sont aussi des fermions, prennent la relève pour assurer l'équilibre de l'étoile. En effet, comme ils sont beaucoup plus massifs, ils ne sont pas relativistes, et leur pression de Fermi s'exprime comme :
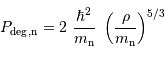
Elle varie donc en fonction du rayon comme 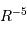 . On assiste alors à un nouvel équilibre, atteint pour un rayon bien plus petit que pour une naine blanche, en raison du facteur
. On assiste alors à un nouvel équilibre, atteint pour un rayon bien plus petit que pour une naine blanche, en raison du facteur 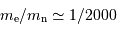 .
.
Ce nouvel équilibre se caractérise par un rayon, estimé en km :
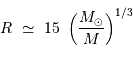
Masse volumique
Dans ces conditions, la masse volumique atteint des valeurs gigantesques :
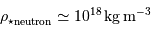
On retrouve en fait la masse volumique de la matière nucléaire. L'étoile à neutrons est analogue à une noyau surdimensionné de nombre de masse 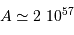 .
.


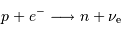

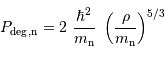
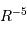 . On assiste alors à un nouvel équilibre, atteint pour un rayon bien plus petit que pour une naine blanche, en raison du facteur
. On assiste alors à un nouvel équilibre, atteint pour un rayon bien plus petit que pour une naine blanche, en raison du facteur 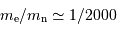 .
.
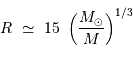
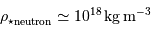
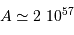 .
.