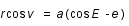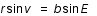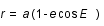Les mouvements de la Terre et de la Lune
Auteur: Patrick Rocher
- Introduction
- Présentation historique
- Introduction
- Les représentations mythologiques
- Mouvement de la Terre
- Introduction
- Mouvement de la Terre autour du Soleil
- En savoir plus: Eléments orbitaux kepleriens de l'orbite terrestre
- En savoir plus: Eléments orbitaux kepleriens de l'orbite terrestre-2
- Exercice
- Mouvement orbital de la Lune
- Introduction
- La mouvement de la Lune autour de la Terre
- En savoir plus: La définition des éléments elliptiques
- En savoir plus: La définition des éléments elliptiques-2
- En savoir plus: La définition des éléments elliptiques-3
- Mouvement de la Lune et périodes de révolution
- Introduction
- Périodes de révolutions de la Lune
- En savoir plus: Les éléments elliptiques moyens de l'orbite lunaire
- En savoir plus: Les éléments elliptiques moyens de l'orbite lunaire-2
- En savoir plus: Les variations des éléments elliptiques de la Lune
- En savoir plus: Les variations des éléments elliptiques de la Lune-2
- Les phases de la Lune
- Introduction
- Les phases de la Lune-1
- Les phases de la Lune-2
- Les phases de la Lune-3
- En savoir plus: La lunaison moyenne, le mois lunaire
- En savoir plus: La lunaison vraie
- Exercice
Introduction
 Prérequis
Prérequis
Aucun
 Introduction
Introduction
Nous présentons d'abord les mouvements de la Terre autour du soleil en décrivant les éléments orbitaux képlérien. Nous traitons ensuite les mouvements de la Lune autour de la Terre en définissant les éléments elliptiques, puis en décrivant différentes périodes de révolutions. Finalement nous présentons les phases de la Lune.
Résumé
Les mouvements de la Terre et de la Lune seront abordés dans un premier temps, puis les phases de la Lune.
Présentation historique
Introduction
 Introduction
Introduction
Dans la quasi-totalité des cultures anciennes et des sociétés sans écriture, les éclipses de Lune et plus encore les éclipses de Soleil, ont été attribuées à des causes surnaturelles, l'intervention d'un dieu, d'un démon ou d'un animal maléfique essayant d'éteindre ou de dévorer l'un des deux luminaires.
Les représentations mythologiques
Ainsi en Asie, un dragon céleste essayait de dévorer la Lune et le Soleil, d'ailleurs le plus ancien mot chinois pour décrire une éclipse, shih, signifie manger. De même en Inde les deux parties décapitées du démon Vichnou, Rahu et Ketu placées aux noeuds de l'orbite lunaire cherchaient à dévorer la Lune et le Soleil. Chez les Mayas, l'éclipse de Soleil est représentée par un serpent mordant le Soleil, au Yucatán, on l'appelle Chibil Chin ce qui signifie textuellement «Morsure du Soleil», de nos jours certains Mayas, tels que les Yucatèques ou les Chols considèrent les éclipses comme une bataille entre le Soleil et la Lune, ils déconseillent aux femmes enceintes d'observer ce phénomène sous peine de mettre au monde un enfant difforme! Les Aztèques ont aussi élaboré des théories concernant les éclipses de Soleil : au cours des éclipses un monstre appelé Tzitzimine descend sur Terre pour dévorer l'humanité, seule une série de sacrifices peut conjurer ce danger. Dans la mythologie germanique, le Soleil et la Lune sont poursuivis par deux loups célestes, Moongarm et Fenris et c'est la lutte entre ces deux monstres qui provoque les éclipses. Comme on le constate toutes les représentations mythologiques des éclipses ont un aspect néfaste, on conjurait ce mauvais sort de différentes façons : en faisant du bruit, en tirant des flèches sur le monstre dévoreur, en entrant dans l'eau ou plus grave à l'aide de sacrifices.
Cette peur engendrée par les éclipses va inciter les astronomes et astrologues de l'Antiquité à prédire le retour de ces phénomènes célestes. Le concept du dragon dévoreur de Lune et de Soleil a été repris par les grecs et les romains, c'est pour cette raison que les noeuds de l'orbite lunaire portent les noms de Caput et Cauda Draconis (la tête et la queue du dragon) et que l'intervalle séparant deux passages de la Lune par un des noeuds de son orbite porte le nom de révolution draconitique.
Il faut noter que bien que ces phénomènes soient parfaitement expliqués, on trouve encore, à la fin du XXe siècle des olibrius pour prédire la fin du monde et la chute de la station MIR place de la Concorde le jour de l'éclipse de Soleil du 11 août 1999. Le plus grave n'étant pas la prédiction en elle-même mais sa diffusion massive par les médias !
Mouvement de la Terre
Introduction
 Introduction
Introduction
Dans cette section nous allons présenter les paramètres orbitaux de la Terre dans le plan défini par sa trajectoire.
Mouvement de la Terre autour du Soleil
En première approximation on peut supposer que le mouvement de la Terre autour du Soleil obéit aux trois lois de Kepler. La Terre parcourt donc une orbite elliptique plane autour du Soleil, le Soleil étant situé à l'un des foyers de l'ellipse. Le plan de cette orbite s'appelle le plan de l'écliptique, car c'est lorsque la pleine Lune ou la nouvelle Lune est proche de ce plan qu'il y a une possibilité d'éclipses de Lune ou de Soleil. Ce plan sert de plan de base (Oxy) au repère de coordonnées polaires écliptiques, l'axe Oz de ce repère est normal au plan de l'écliptique et il est orienté de sorte que la trajectoire de la Terre soit dans le sens direct. Les deux coordonnées angulaires polaires écliptiques portent les noms de longitude écliptique et de latitude écliptique. Dans ce modèle keplerien du mouvement de la Terre, la latitude de la Terre est toujours nulle. Sur son orbite la Terre passe par deux positions particulières situées aux extrémités de la ligne des apsides (le grand-axe de l'ellipse) : l'aphélie correspondant à la distance maximale entre la Terre et le Soleil, et le périhélie correspondant à la distance minimale entre la Terre et le Soleil. Suite à la deuxième loi de Kepler, à l'aphélie la vitesse de la Terre est minimale et au périhélie elle est maximale. Ainsi la vitesse angulaire de la Terre progresse 7% plus vite au périhélie qu'à l'aphélie.
Dans l'étude des éclipses, on utilise le mouvement apparent du Soleil autour de la Terre. Dans ce mouvement le Soleil parcourt une orbite elliptique autour de la Terre, l'orbite a les mêmes caractéristiques que la trajectoire de la Terre autour du Soleil. Cette représentation est correcte d'un point de vue cinématique (changement d'origine du repère), mais n'a aucun sens d'un point de vue dynamique.
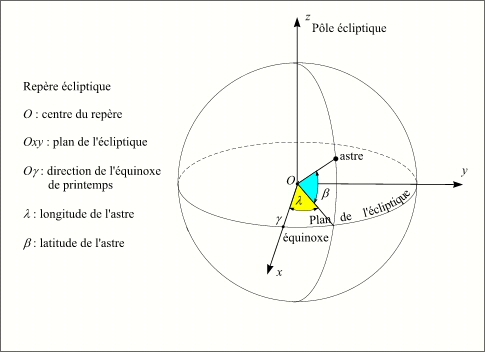
Sphère céleste écliptique.
Crédit : IMCCE/Patrick Rocher
En savoir plus: Eléments orbitaux kepleriens de l'orbite terrestre
 En savoir plus
En savoir plus
Le mouvement elliptique de la Terre a lieu dans le plan de l'écliptique, l'ellipse est donc définie géométriquement par la connaissance de la longitude du périastre : ω (angle formé par son demi-grand axe et l'axe Ox), de son demi-grand axe a et de son excentricité e. Le mouvement de la Terre sur l'ellipse est connu lorsque l'on connaît pour une date origine T0 sa longitude λ et son moyen mouvement n.
En réalité, suite aux perturbations planétaires l'orbite de la Terre n'est pas keplerienne et ses éléments orbitaux ne sont pas constants mais varient avec le temps.
Le tableau suivant donne les éléments moyens de l'orbite de la Terre dans le repère défini par l'équinoxe et l'écliptique moyens dynamiques inertiels de la date (J2000).
| Paramètres de l'orbite |
Valeurs au 1er janvier 2000 à 12h |
| demi-grand axe : a
|
1,000 001 017 8 ua |
| excentricité : e
|
0,016 708 634 2 |
| longitude du périhélie : ϖ
|
102,937 348 08° |
| longitude de la Terre : λ
|
100,466 456 83° |
| moyen mouvement : n
|
1296027711,03429"/millier d'année julienne ~ 0,985 647 358°/jour |
Comme ces éléments sont donnés dans le repère moyen de la date, repère tenant compte de la précession des équinoxes, l'inclinaison de l'orbite est nulle et le rapport 360°/n donne la période de révolution tropique de la Terre autour du Soleil (365,2421904 jours). Pour avoir la révolution sidérale de la Terre (365,2563632 jours), il faut utiliser le moyen mouvement donné dans le repère fixe J2000 (n = 0,9856091125°/jour).
En savoir plus: Eléments orbitaux kepleriens de l'orbite terrestre-2
 En savoir plus
En savoir plus
- La distance entre le Soleil et la Terre au périhélie est donnée par la formule Δ = a . (1 - e).
- La distance entre le Soleil et la Terre à l'aphélie est donnée par la formule Δ = a . (1 + e).
- Le demi-grand axe a, le demi-petit axe b et l'excentricité e sont liés par la relation suivante : e2 = (a2 - b2) / a2.
- La distance c entre le centre de l'ellipse et un de ses foyers est donnée par c = e.a
- Le diamètre apparent D du Soleil vu du centre de la Terre est donné par la formule : D = 2 arctg(Rs/Δ), où Δ est la distance Terre-Soleil et Rs le rayon du disque solaire.
- Le moyen mouvement n est lié au demi-grand axe a de l'ellipse par la troisième loi de Kepler : n2 a3 = constante.
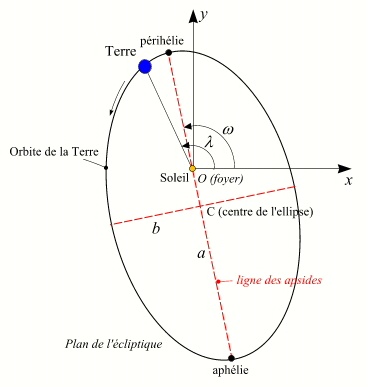
Éléments de l'orbite keplerienne de la Terre;
Crédit : IMCCE/Patrick Rocher
 Remarque
Remarque
Sur cette figure l'excentricité de l'orbite terrestre a été fortement exagérée.
Exercice
 Orbite de la Terre
Orbite de la Terre
 Remarque
Remarque
Le tracé de l'orbite de la Terre autour du Soleil en prenant a = 10 cm est un cercle. En effet la différence entre le demi-grand axe et de demi-petit axe est d'environ 14 μm, elle est donc dans l'épaisseur du trait. Par contre, sur la figure, le Soleil n'occupe pas le centre du cercle mais est excentré d'environ 1,7 mm
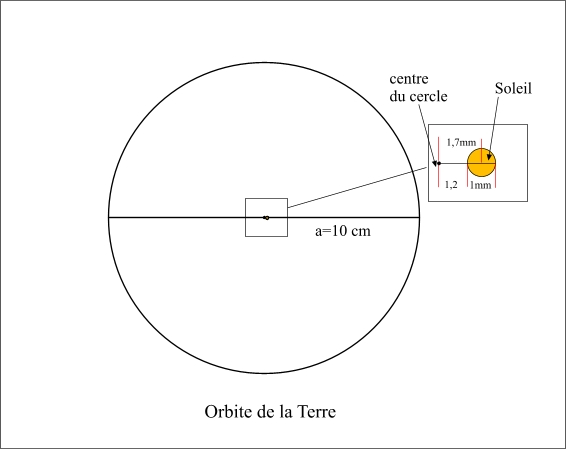
Orbite de la Terre.
Crédit : IMCCE/Patrick Rocher
Question 1)
En utilisant les éléments orbitaux de la Terre donnés dans le supplément de cours, calculer la valeur du demi-petit axe b de l'ellipse, la distance c entre le centre de l'ellipse et son foyer. Puis calculer les distances Terre-Soleil lorsque la Terre est au périhélie et lorsque la Terre est à l'aphélie. Exprimer ces résultats en unités astronomiques, puis en kilomètres en prenant : 1 ua = 149597870 km.
En déduire les valeurs du diamètre apparent du Soleil vu du centre de la Terre, lorsque la Terre est à l'aphélie et lorsque la Terre est au périhélie, on prendra le rayon solaire égal à 696000km. Ensuite, faire un dessin à l'échelle en prenant comme demi-grand axe de l'orbite terrestre une valeur de 10 cm. Calculer les valeurs précédentes à cette échelle, calculer la valeur de a - b.
Que peut-on en conclure ?
Mouvement orbital de la Lune
Introduction
 Introduction
Introduction
Cette section décrit le mouvement orbital de la Lune par rapport au Soleil. Le problème qui était plan dans le cas de la Terre devient spatial car le plan de l'orbite lunaire n'est pas confondu avec le plan de l'orbite terrestre. Il convient donc d'ajouter de paramètres supplémentaires pour positionner le plan de l'orbite par rapport au repère fondamental (plan de l'écliptique ou de l'équateur).
La mouvement de la Lune autour de la Terre
Contrairement au mouvement de la Terre autour du Soleil, qui peut être considéré en première approximation comme keplerien (solution exacte du problème des deux corps), le mouvement de la Lune est beaucoup plus complexe. Une première approximation du mouvement de la Lune est donnée par la résolution d'un problème des trois corps (Soleil, Terre et Lune) appelé problème principal. Dans ce problème le mouvement de la Lune est obtenu en tenant compte de l'attraction du centre de masse de la Terre et des perturbations solaires dans le cadre de la mécanique newtonienne, le mouvement du barycentre Terre-Lune étant représenté par un mouvement keplerien.
La solution complète tient compte de très nombreuses perturbations et les éléments elliptiques se présentent sous la forme de séries semi-analytiques comportant plusieurs milliers de termes, environ 35000 pour la solution ELP2000 de Michèle Chapront-Touzé et Jean Chapront.
Les éléments elliptiques de l'orbite lunaire ne sont donc pas constants, mais varient rapidement avec le temps. Les valeurs du demi-grand axe, de l'excentricité et de l'inclinaison oscillent autour de valeurs moyennes ; la ligne des noeuds de l'orbite et la ligne des apsides sont animées de mouvements circulaires non uniformes.
En tenant compte de ces perturbations, la vitesse angulaire de la Lune peut progresser 29% plus vite à son périgée qu'à son apogée. La variation de distance entre le centre de la Terre et le centre de la Lune va de 56 à 63,8 rayons terrestres selon que la Lune est à son périgée ou à son apogée (la distance moyenne est de 60 rayons terrestres).
En savoir plus: La définition des éléments elliptiques
 En savoir plus
En savoir plus
Les éléments elliptiques sont une série de six paramètres permettant de définir parfaitement une orbite elliptique keplerienne dans le repère écliptique céleste. L'orbite elliptique keplerienne étant la trajectoire d'un corps M gravitant autour d'un corps principal S pour une époque initiale donnée t0.
Trois paramètres déterminent les caractéristiques de l'ellipse et du mouvement du corps dans le plan de l'orbite :
- le demi-grand axe a de l'ellipse,
- l'excentricité e de l'ellipse,
- l'anomalie vraie υ du corps pour l'époque donnée, c'est l'angle formé par la direction du périastre et la direction du corps vues du foyer de l'ellipse.
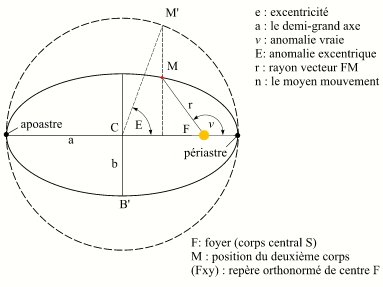
Paramètres de l'ellipse keplerienne.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre donne une représentation de ces paramètres ainsi que d'autres paramètres liés au mouvement elliptique.
En savoir plus: La définition des éléments elliptiques-2
 En savoir plus
En savoir plus
Les formules du problème des deux corps permettent de calculer la position de l'astre sur son orbite pour un instant t quelconque.
L'anomalie moyenne M (parfois notée l dans le cas de la Lune) est donnée par M = n.(t - t0) où n est le moyen mouvement.
Le moyen mouvement n est lié au demi-grand axe a de l'ellipse par la troisième loi de Kepler (n2 a3 = constante).
On passe de l'anomalie moyenne M à l'anomalie excentrique E en résolvant l'équation de Kepler : E - e sin E = M. Cette équation se résout par itérations successives.
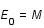
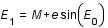
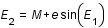
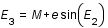 et ainsi de suite.
et ainsi de suite.
Enfin, connaissant l'anomalie excentrique E, l'anomalie vraie v et le rayon vecteur r sont donnés par les équations suivantes :
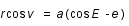
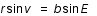
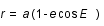
Le plan de l'orbite n'étant pas a priori dans le plan de l'écliptique, ces deux plans se coupent suivant une droite appelée ligne des noeuds ligne des noeuds. Cette ligne des noeuds coupe l'orbite du corps en deux points : le noeud ascendant de l'orbite par lequel passe le corps lorsqu'il passe des latitudes négatives aux latitudes positives et le noeud descendant de l'orbite par lequel passe le corps lorsqu'il passe des latitudes positives aux latitudes négatives.
En savoir plus: La définition des éléments elliptiques-3
 En savoir plus
En savoir plus
Trois angles permettent de positionner le plan de l'orbite dans l'espace :
- La longitude du noeud ascendant de l'orbite Ω, c'est l'angle formé par la direction de l'axe 0x et la direction du noeud ascendant de l'orbite,
- l'inclinaison de l'orbite i, c'est l'angle formé par le plan de l'écliptique et le plan de l'orbite,
- l'argument du périastre ω, c'est l'angle formé par la direction du noeud ascendant et la direction du périastre.
Parfois on donne l'angle ϖ = Ω + ω que l'on appelle longitude du périastre.
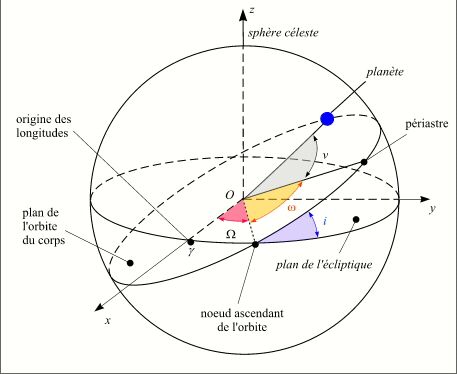
Éléments de l'orbite keplerienne
Crédit : IMCCE/Patrick Rocher
Mouvement de la Lune et périodes de révolution
Introduction
 Introduction
Introduction
Dans cette section nous allons définir les différentes périodes de révolution qui se rattachent au mouvement de la Lune. Les pages "pour en savoir plus" donnent les valeurs des différents paramètres orbitaux et leurs variations au cours du temps.
Périodes de révolutions de la Lune
Le tableau suivant donne les périodes de révolutions moyennes de la Lune.
| Nom de la période |
Durée en jours |
Définition |
| période sidérale |
27,321 661 547 |
retour dans la même direction par rapport aux étoiles |
| période anomalistique |
27,554 549 878 |
retour au périgée de l'orbite |
| période synodique |
29,530 588 853 |
retour de la même phase lunaire |
| période draconitique |
27,212 220 817 |
retour par le même noeud de l'orbite |
| période tropique |
27,321 582 249 |
retour par la direction de l'équinoxe. |
 Remarque
Remarque
Toutes les périodes décrites ci-dessus font intervenir la longitude moyenne de la Lune, ce sont donc des périodes de révolutions moyennes et non des périodes de révolutions vraies. Les périodes de révolutions vraies varient continuellement et ne sont pratiquement jamais égales aux périodes de révolutions moyennes. Ainsi, par exemple, l'intervalle de temps qui sépare deux nouvelles Lunes (lunaison vraie) peut présenter des écarts de plus ou moins 7h avec la valeur de la période synodique moyenne (lunaison moyenne).
En savoir plus: Les éléments elliptiques moyens de l'orbite lunaire
 En savoir plus
En savoir plus
Le tableau suivant donne les éléments elliptiques moyens de la Lune rapportés à l'écliptique et à l'équinoxe moyens de la date pour l'époque J2000 (1 janvier 2000 à 12h).
| Éléments |
Valeurs |
Mouvements dus aux perturbations |
| Demi-grand axe a
|
383 397,7916 km |
|
| Excentricité e
|
0,055 545 526 |
|
| Inclinaison i
|
5,156 689 83° |
|
| Longitude du noeud Ω
|
125,044 555 04° |
mouvement rétrograde : (-19.3413618°/an) |
| Longitude du périgée ϖ
|
83,353 242 99° |
mouvement direct : (+40,690137°/an) |
| Longitude moyenne L
|
218,316 654 36° |
|
L'anomalie moyenne M de la Lune est donnée par : M = n (t - t0) où n est le moyen mouvement de la Lune.
En savoir plus: Les éléments elliptiques moyens de l'orbite lunaire-2
 En savoir plus
En savoir plus
La longitude vraie de la Lune Λ est donnée par : Λ = Ω + ω + υ = ϖ + υ où υ est l'anomalie vraie.
La longitude moyenne de la Lune L est donnée par : L = Ω + ω + M = ϖ + M = ϖ + n (t - t0). La période de révolution de la longitude moyenne est égale à la révolution sidérale de la Lune, la période sidérale est l'intervalle de temps qui s'écoule en moyenne entre deux passages de la Lune dans une même direction par rapport aux étoiles.
L'anomalie moyenne M = L - ω représente l'angle entre la direction du périgée et la longitude moyenne de la Lune, sa période de révolution s'appelle la période anomalistique, elle représente l'intervalle de temps qui s'écoule en moyenne entre deux passages de la Lune à son périgée, elle diffère de la révolution sidérale car la ligne des apsides (donc le périgée) est animée d'un mouvement de rotation dans le sens direct.
L'angle D = L - Ls est la différence entre la longitude moyenne de la Lune et la longitude moyenne du Soleil. Les phases de la Lune sont liées, non à cet angle, mais à la différence entre les longitudes vraies des deux corps. Pour la nouvelle Lune, le premier quartier, la pleine Lune et le dernier quartier cette différence vaut respectivement 0°, 90°, 180° et 270°. Par contre la période moyenne qui ramène la Lune dans une même phase que l'on appelle la période synodique ou lunaison moyenne est la période de l'angle D.
L'angle F = L - Ω est la différence entre la longitude moyenne de la Lune et la direction du noeud ascendant de son orbite. Sa période de révolution s'appelle période draconitique, elle représente l'intervalle de temps qui s'écoule en moyenne entre deux passages de la Lune au noeud ascendant de son orbite, elle diffère de la révolution sidérale car la ligne des noeuds est animée d'un mouvement de rotation dans le sens rétrograde.
En savoir plus: Les variations des éléments elliptiques de la Lune
 En savoir plus
En savoir plus
Nous avons vu que, sous l'action de nombreuses perturbations, les éléments orbitaux de la Lune ne sont pas constants, mais varient avec le temps. Le tableau suivant donne les plus grosses variations de ces éléments.
| Éléments |
Amplitude |
Période |
Amplitude |
Période |
|
a
|
3400,4 km |
14.76 j |
-635,6 km |
31,81j |
|
e
|
0,014217 |
31,81j |
0,008551 |
173,31j |
|
i
|
|
|
8,105' |
173,31j |
|
ϖ
|
-15,448° |
31,81j |
-9,642° |
205,9j |
|
Ω
|
|
|
-1,4979° |
173,31j |
On constate que ces variations présentent de très fortes amplitudes sur des périodes de temps relativement courtes. Ainsi l'excentricité varie de plus ou moins 0,014217 sur une période de 31,81 jours ce qui représente un écart de plus de 25% de la valeur moyenne !
En savoir plus: Les variations des éléments elliptiques de la Lune-2
 En savoir plus
En savoir plus
La série suivante donne les premiers termes permettant le calcul de la longitude vraie de la Lune ainsi que leur nom et l'époque de leur découverte :
Λ = L + (6,288 8° sin M + 0,213 6° sin 2M)
équation du centre : connue depuis Hipparque (~150 av. J.-C.)
+ 1,274 0° sin (2D - M)
évection (période 31,81 jours) : découverte par Ptolémée (milieu du IIe siècle)
+ 0,658 3° sin 2D
variation (période 14,76 jours) : découverte par Tycho Brahé (XVIe siècle)
- 0,185 1° sin M'
équation annuelle (période 1 an) : découverte par Tycho Brahé (XVIe siècle)
- 0,114 3° sin 2F
réduction à l'écliptique (période 13,6 jours)
 Remarque
Remarque
Comme on le verra par la suite, les diamètres apparents de la Lune et du Soleil vus depuis la Terre sont de l'ordre du demi-degré, donc pour prédire une éclipse du Soleil il faut obligatoirement connaître la position de ces deux corps avec une précision inférieure à ce demi-degré. Pour la Lune, il faut donc connaître l'équation du centre et l'évection, la connaissance de la variation n'est pas nécessaire car le terme sin 2D est nul à la pleine Lune et à la nouvelle Lune (D = 0° et D = 180°). Il était donc impossible de prédire la visibilité d'une éclipse de Soleil en un lieu donné avant le milieu du IIe siècle, époque de la découverte de l'évection par Claude Ptolémée.
Les phases de la Lune
Introduction
 Introduction
Introduction
Dans cette section nous allons étudier et décrire les phases lunaires et les différents noms qui leurs sont attribués.
Les phases de la Lune-1
Comme nous venons de le voir, la Lune tourne autour de la Terre dans un mouvement d'ouest en est (dans le sens direct). Elle effectue un tour complet autour de la Terre au cours d'une révolution sidérale de 27,321661547 jours. Au cours de sa révolution, depuis la Terre, on ne voit pas la partie éclairée de la Lune sous un même angle, cela constitue les phases de la Lune. On distingue quatre positions particulières.
Lorsque la Lune et le Soleil ont la même longitude, on dit qu'ils sont en conjonction, c'est la nouvelle Lune. Lorsque la longitude de la Lune est à 180° de la longitude du Soleil, on dit qu'ils sont en opposition, c'est la pleine Lune. À la nouvelle Lune, la Lune est devant le Soleil, elle se lève et se couche donc presque en même temps que lui. À la pleine Lune, la Lune est à l'opposée du Soleil, donc elle se lève lorsqu'il se couche et elle se couche lorsqu'il se lève. Ainsi la nouvelle Lune n'est levée que le jour et la pleine Lune n'est levée que la nuit. La pleine Lune et la nouvelle Lune portent également le nom de syzygies.
Les phases de la Lune-2
Les phases comprises entre la nouvelle Lune et la pleine Lune s'appellent phases croissantes et les phases comprises entre la pleine Lune et la nouvelle Lune s'appellent phases décroissantes. Lorsque la longitude de la Lune est à 90° vers l'est de la longitude du Soleil, on aperçoit uniquement une moitié du disque lunaire éclairé, c'est le premier quartier de Lune, on dit également que la Lune est en quadrature Est. Lorsque la longitude de la Lune est à 90° vers l'ouest (270° vers l'est) de la longitude du Soleil, on aperçoit l'autre moitié du disque lunaire éclairé, c'est le dernier quartier de Lune, on dit également que la Lune est en quadrature Ouest. Le premier quartier est donc compris entre la nouvelle Lune et la pleine Lune et le dernier quartier est compris entre la pleine Lune et la nouvelle Lune. Les aspects du premier et du dernier quartier de Lune sont inversés selon que l'on se trouve dans l'hémisphère nord ou dans l'hémisphère sud. Ainsi le premier quartier vu depuis l'hémisphère nord ressemble au dernier quartier vu depuis l'hémisphère sud et inversement. Le premier quartier se trouvant 90° à l'est du Soleil, il est visible l'après midi à l'est et dans la première partie de la nuit à l'ouest. Le dernier quartier étant à 90° à l'ouest du Soleil, il est visible la seconde moitié de la nuit à l'est et dans la matinée à l'ouest. Entre la nouvelle Lune et les quartiers de Lune, la phase lunaire a l'aspect d'un croissant, entre les quartiers et la pleine Lune, la Lune a la forme d'une bosse et on la qualifie de gibbeuse.
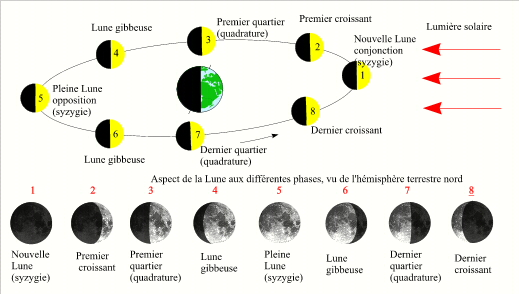
Les phases lunaires
Crédit : IMCCE/Patrick Rocher
Les phases de la Lune-3
Il y a éclipse de Soleil lorsque la Lune passe devant le Soleil et éclipse de Lune lorsque la Lune passe dans l'ombre de la Terre. Les éclipses de Soleil ont donc toujours lieu au voisinage de la conjonction (nouvelle Lune) et les éclipses de Lune ont toujours lieu au voisinage de l'opposition (pleine Lune). Si l'orbite de la Lune était dans le plan de l'orbite du Soleil apparent autour de la Terre (écliptique) il y aurait des éclipses de Soleil à chaque nouvelle Lune et des éclipses de Lune à chaque pleine Lune. Comme les éclipses de Soleil ont lieu à la nouvelle Lune, elles ne sont visibles en un lieu donné que le jour, cela parait évident. De même comme les éclipses de Lune ont lieu à la pleine Lune, elles ne sont visibles en un lieu donné que la nuit.
En savoir plus: La lunaison moyenne, le mois lunaire
 En savoir plus
En savoir plus
La lunaison moyenne est l'intervalle de temps qui s'écoule en moyenne entre deux mêmes phases, c'est la combinaison de deux mouvements moyens : le mouvement moyen de la Lune autour de la Terre, dont la période moyenne de révolution est la révolution sidérale de la Lune SL = 27,321661547 jours (27 jours 7h 43m 11,56s), et le mouvement moyen du Soleil apparent autour de la Terre (ou de la Terre autour du Soleil), dont la période moyenne de révolution est la révolution sidérale du Soleil (ou de la Terre) SS = 365,2563632 jours. Nous avons donc deux mouvements moyens de période SS et SL dans le même sens, l'intervalle de temps L qui sépare deux nouvelles Lunes, appelée révolution synodique moyenne, est solution de l'équation suivante :
1/SL - 1/SS = 1/L
En l'on trouve L = 29,53058885 jours soit 29 jours 12h 44m 2,88s.
La révolution synodique moyenne porte également les noms de lunaison moyenne et de mois lunaire moyen.
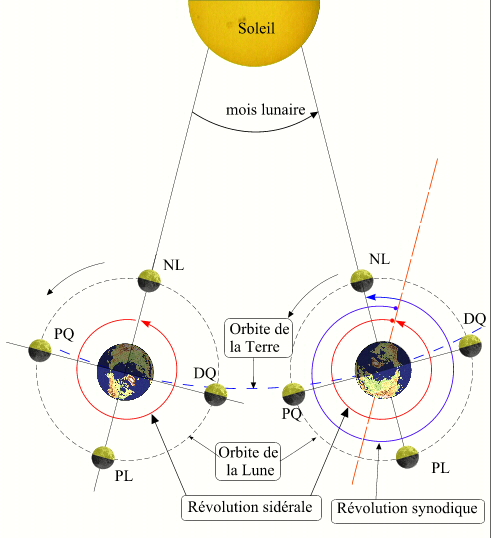
Révolutions sidérale et synodique
Crédit : IMCCE/Patrick Rocher
En savoir plus: La lunaison vraie
 En savoir plus
En savoir plus
La révolution synodique moyenne de la Lune correspond à une valeur moyenne, en réalité comme nous l'avons déjà vu ni le mouvement orbital de la Lune ni le mouvement orbital de la Terre ne sont uniformes. La vitesse angulaire de la Lune est maximale au périgée et minimale à l'apogée. De même la vitesse de la Terre est maximale en janvier lorsqu'elle est au périhélie et minimale en juillet lorsqu'elle est à l'aphélie. La lunaison vraie va donc être différente de la lunaison moyenne. De plus la période séparant deux nouvelles Lunes vraies ne sera pas égale à la période séparant deux pleines Lunes vraies. Le graphique ci-contre nous donne les écarts en heures et fraction d'heure entre la lunaison vraie et la lunaison moyenne. On constate que ces écarts peuvent atteindre plus ou moins sept heures, ce qui est énorme compte tenu de la vitesse angulaire de la Lune, l'écart en longitude entre la Lune vraie et la Lune moyenne peut atteindre jusqu'à 7,5°. Cette valeur est à comparer avec les diamètres apparents de la Lune et du Soleil (0,5°).
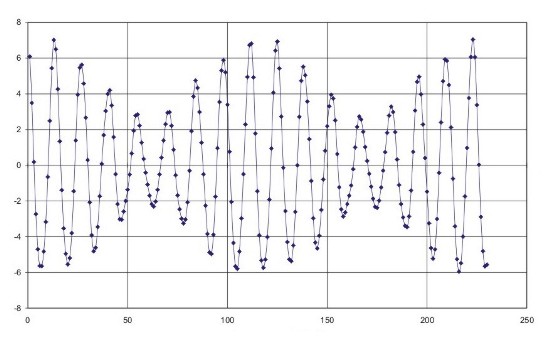
Écarts entre la lunaison vraie et la lunaison moyenne sur une période de 18,6 ans
Crédit : IMCCE/Patrick Rocher
Ce graphique fait également apparaître une période de 8,84 ans correspondant à la projection en longitude du mouvement du périgée de la Lune. En effet la ligne des apsides de la Lune tourne dans le sens direct dans le plan de l'orbite lunaire, ce mouvement projeté dans le plan de l'écliptique et combiné avec le mouvement rétrograde des noeuds de l'orbite lunaire produit un mouvement en longitude de la projection du périgée de 40,690137°/an soit une période d'environ 8,84 ans. Il est normal que l'on retrouve cette période dans la variation de la lunaison vraie car la vitesse angulaire de la Lune varie avec l'anomalie vraie.
Exercice
 Cacul de la lunaison moyenne
Cacul de la lunaison moyenne
Question 1)
Nous avons vu que la lunaison moyenne est la combinaison de deux mouvements : le mouvement moyen de la Lune autour de la Terre et le mouvement moyen du Soleil apparent autour de la Terre. Ces deux mouvements se font dans le même sens. Le calcul de la lunaison moyenne a été fait dans le cours à partir de la période de révolution sidérale de la Lune et de la révolution sidérale du Soleil. Refaites ce calcule à l'aide des révolutions tropiques de la Lune et du Soleil. Trouve-t-on la même valeur? Pourquoi?
On donne les valeurs suivantes :
révolution tropique de la Lune : TL = 27,321 582 249 jours,
révolution tropique de la Terre ( donc du Soleil apparent) : TS = 365,242 190 04 jours.
 Prérequis
Prérequis Introduction
Introduction



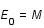
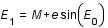
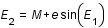
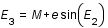 et ainsi de suite.
et ainsi de suite.