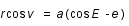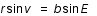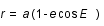Introduction
Introduction
Cette section décrit le mouvement orbital de la Lune par rapport au Soleil. Le problème qui était plan dans le cas de la Terre devient spatial car le plan de l'orbite lunaire n'est pas confondu avec le plan de l'orbite terrestre. Il convient donc d'ajouter de paramètres supplémentaires pour positionner le plan de l'orbite par rapport au repère fondamental (plan de l'écliptique ou de l'équateur).
Contrairement au mouvement de la Terre autour du Soleil, qui peut être considéré en première approximation comme keplerien (solution exacte du problème des deux corps), le mouvement de la Lune est beaucoup plus complexe. Une première approximation du mouvement de la Lune est donnée par la résolution d'un problème des trois corps (Soleil, Terre et Lune) appelé problème principal. Dans ce problème le mouvement de la Lune est obtenu en tenant compte de l'attraction du centre de masse de la Terre et des perturbations solaires dans le cadre de la mécanique newtonienne, le mouvement du barycentre Terre-Lune étant représenté par un mouvement keplerien.
La solution complète tient compte de très nombreuses perturbations et les éléments elliptiques se présentent sous la forme de séries semi-analytiques comportant plusieurs milliers de termes, environ 35000 pour la solution ELP2000 de Michèle Chapront-Touzé et Jean Chapront.
Les éléments elliptiques de l'orbite lunaire ne sont donc pas constants, mais varient rapidement avec le temps. Les valeurs du demi-grand axe, de l'excentricité et de l'inclinaison oscillent autour de valeurs moyennes ; la ligne des noeuds de l'orbite et la ligne des apsides sont animées de mouvements circulaires non uniformes.
En tenant compte de ces perturbations, la vitesse angulaire de la Lune peut progresser 29% plus vite à son périgée qu'à son apogée. La variation de distance entre le centre de la Terre et le centre de la Lune va de 56 à 63,8 rayons terrestres selon que la Lune est à son périgée ou à son apogée (la distance moyenne est de 60 rayons terrestres).
 En savoir plus
En savoir plus
Les éléments elliptiques sont une série de six paramètres permettant de définir parfaitement une orbite elliptique keplerienne dans le repère écliptique céleste. L'orbite elliptique keplerienne étant la trajectoire d'un corps M gravitant autour d'un corps principal S pour une époque initiale donnée t0.
Trois paramètres déterminent les caractéristiques de l'ellipse et du mouvement du corps dans le plan de l'orbite :
- le demi-grand axe a de l'ellipse,
- l'excentricité e de l'ellipse,
- l'anomalie vraie υ du corps pour l'époque donnée, c'est l'angle formé par la direction du périastre et la direction du corps vues du foyer de l'ellipse.
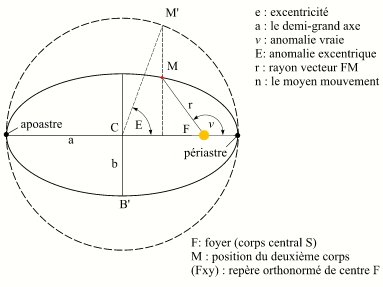
Paramètres de l'ellipse keplerienne.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre donne une représentation de ces paramètres ainsi que d'autres paramètres liés au mouvement elliptique.
 En savoir plus
En savoir plus
Les formules du problème des deux corps permettent de calculer la position de l'astre sur son orbite pour un instant t quelconque.
L'anomalie moyenne M (parfois notée l dans le cas de la Lune) est donnée par M = n.(t - t0) où n est le moyen mouvement.
Le moyen mouvement n est lié au demi-grand axe a de l'ellipse par la troisième loi de Kepler (n2 a3 = constante).
On passe de l'anomalie moyenne M à l'anomalie excentrique E en résolvant l'équation de Kepler : E - e sin E = M. Cette équation se résout par itérations successives.
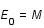
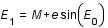
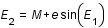
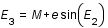 et ainsi de suite.
et ainsi de suite.
Enfin, connaissant l'anomalie excentrique E, l'anomalie vraie v et le rayon vecteur r sont donnés par les équations suivantes :
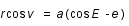
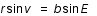
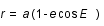
Le plan de l'orbite n'étant pas a priori dans le plan de l'écliptique, ces deux plans se coupent suivant une droite appelée ligne des noeuds ligne des noeuds. Cette ligne des noeuds coupe l'orbite du corps en deux points : le noeud ascendant de l'orbite par lequel passe le corps lorsqu'il passe des latitudes négatives aux latitudes positives et le noeud descendant de l'orbite par lequel passe le corps lorsqu'il passe des latitudes positives aux latitudes négatives.
 En savoir plus
En savoir plus
Trois angles permettent de positionner le plan de l'orbite dans l'espace :
- La longitude du noeud ascendant de l'orbite Ω, c'est l'angle formé par la direction de l'axe 0x et la direction du noeud ascendant de l'orbite,
- l'inclinaison de l'orbite i, c'est l'angle formé par le plan de l'écliptique et le plan de l'orbite,
- l'argument du périastre ω, c'est l'angle formé par la direction du noeud ascendant et la direction du périastre.
Parfois on donne l'angle ϖ = Ω + ω que l'on appelle longitude du périastre.
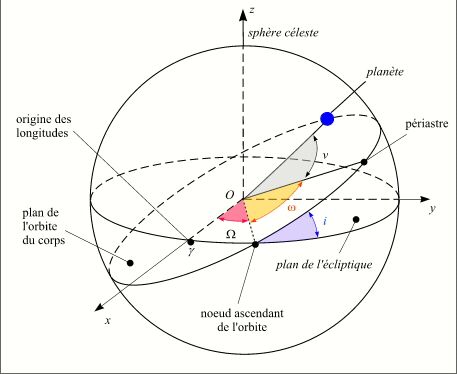
Éléments de l'orbite keplerienne
Crédit : IMCCE/Patrick Rocher
 Introduction
Introduction
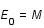
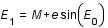
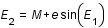
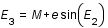 et ainsi de suite.
et ainsi de suite.