Introduction
Dans cette section nous allons présenter les paramètres orbitaux de la Terre dans le plan défini par sa trajectoire.
IntroductionDans cette section nous allons présenter les paramètres orbitaux de la Terre dans le plan défini par sa trajectoire.
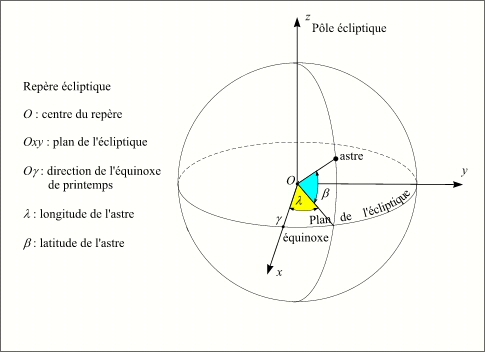
En première approximation on peut supposer que le mouvement de la Terre autour du Soleil obéit aux trois lois de Kepler. La Terre parcourt donc une orbite elliptique plane autour du Soleil, le Soleil étant situé à l'un des foyers de l'ellipse. Le plan de cette orbite s'appelle le plan de l'écliptique, car c'est lorsque la pleine Lune ou la nouvelle Lune est proche de ce plan qu'il y a une possibilité d'éclipses de Lune ou de Soleil. Ce plan sert de plan de base (Oxy) au repère de coordonnées polaires écliptiques, l'axe Oz de ce repère est normal au plan de l'écliptique et il est orienté de sorte que la trajectoire de la Terre soit dans le sens direct. Les deux coordonnées angulaires polaires écliptiques portent les noms de longitude écliptique et de latitude écliptique. Dans ce modèle keplerien du mouvement de la Terre, la latitude de la Terre est toujours nulle. Sur son orbite la Terre passe par deux positions particulières situées aux extrémités de la ligne des apsides (le grand-axe de l'ellipse) : l'aphélie correspondant à la distance maximale entre la Terre et le Soleil, et le périhélie correspondant à la distance minimale entre la Terre et le Soleil. Suite à la deuxième loi de Kepler, à l'aphélie la vitesse de la Terre est minimale et au périhélie elle est maximale. Ainsi la vitesse angulaire de la Terre progresse 7% plus vite au périhélie qu'à l'aphélie.
Dans l'étude des éclipses, on utilise le mouvement apparent du Soleil autour de la Terre. Dans ce mouvement le Soleil parcourt une orbite elliptique autour de la Terre, l'orbite a les mêmes caractéristiques que la trajectoire de la Terre autour du Soleil. Cette représentation est correcte d'un point de vue cinématique (changement d'origine du repère), mais n'a aucun sens d'un point de vue dynamique.
En savoir plusLe mouvement elliptique de la Terre a lieu dans le plan de l'écliptique, l'ellipse est donc définie géométriquement par la connaissance de la longitude du périastre : ω (angle formé par son demi-grand axe et l'axe Ox), de son demi-grand axe a et de son excentricité e. Le mouvement de la Terre sur l'ellipse est connu lorsque l'on connaît pour une date origine T0 sa longitude λ et son moyen mouvement n.
En réalité, suite aux perturbations planétaires l'orbite de la Terre n'est pas keplerienne et ses éléments orbitaux ne sont pas constants mais varient avec le temps.
Le tableau suivant donne les éléments moyens de l'orbite de la Terre dans le repère défini par l'équinoxe et l'écliptique moyens dynamiques inertiels de la date (J2000).
| Paramètres de l'orbite | Valeurs au 1er janvier 2000 à 12h |
|---|---|
| demi-grand axe : a | 1,000 001 017 8 ua |
| excentricité : e | 0,016 708 634 2 |
| longitude du périhélie : ϖ | 102,937 348 08° |
| longitude de la Terre : λ | 100,466 456 83° |
| moyen mouvement : n | 1296027711,03429"/millier d'année julienne ~ 0,985 647 358°/jour |
Comme ces éléments sont donnés dans le repère moyen de la date, repère tenant compte de la précession des équinoxes, l'inclinaison de l'orbite est nulle et le rapport 360°/n donne la période de révolution tropique de la Terre autour du Soleil (365,2421904 jours). Pour avoir la révolution sidérale de la Terre (365,2563632 jours), il faut utiliser le moyen mouvement donné dans le repère fixe J2000 (n = 0,9856091125°/jour).
En savoir plus
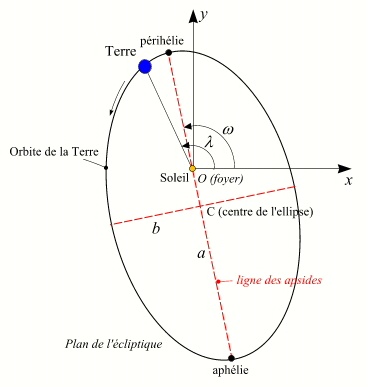
RemarqueSur cette figure l'excentricité de l'orbite terrestre a été fortement exagérée.
Orbite de la TerreRemarqueLe tracé de l'orbite de la Terre autour du Soleil en prenant a = 10 cm est un cercle. En effet la différence entre le demi-grand axe et de demi-petit axe est d'environ 14 μm, elle est donc dans l'épaisseur du trait. Par contre, sur la figure, le Soleil n'occupe pas le centre du cercle mais est excentré d'environ 1,7 mm
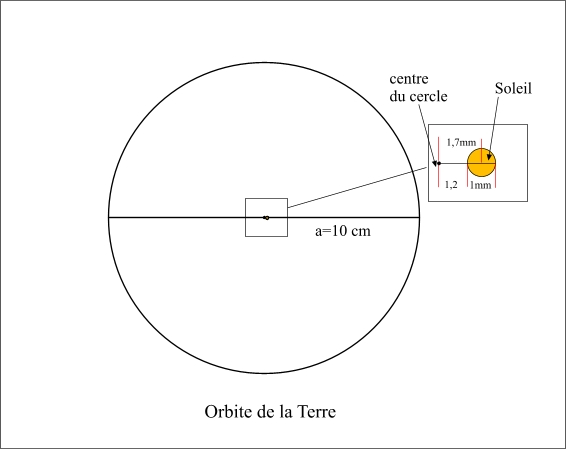
En utilisant les éléments orbitaux de la Terre donnés dans le supplément de cours, calculer la valeur du demi-petit axe b de l'ellipse, la distance c entre le centre de l'ellipse et son foyer. Puis calculer les distances Terre-Soleil lorsque la Terre est au périhélie et lorsque la Terre est à l'aphélie. Exprimer ces résultats en unités astronomiques, puis en kilomètres en prenant : 1 ua = 149597870 km.
En déduire les valeurs du diamètre apparent du Soleil vu du centre de la Terre, lorsque la Terre est à l'aphélie et lorsque la Terre est au périhélie, on prendra le rayon solaire égal à 696000km. Ensuite, faire un dessin à l'échelle en prenant comme demi-grand axe de l'orbite terrestre une valeur de 10 cm. Calculer les valeurs précédentes à cette échelle, calculer la valeur de a - b.
Que peut-on en conclure ?