Occultation par un objet entouré d'une atmosphère
Lorsque qu'un objet du système solaire entouré d'une atmosphère occulte une étoile, la haute atmosphère joue le rôle de lentille.
La phase d'extinction présente des fluctuations d'intensité, reliées à la stratification des couches atmosphériques.

Crédit :
Observatoire de Paris/ASM
Observations multisites
L'observation de l'occultation sur plusieurs sites permet de déterminer les positions et longueurs des diverses cordes correspondant aux conditions locales d'observation de l'occultation. On en déduit la taille et la forme de l'objet occultant.
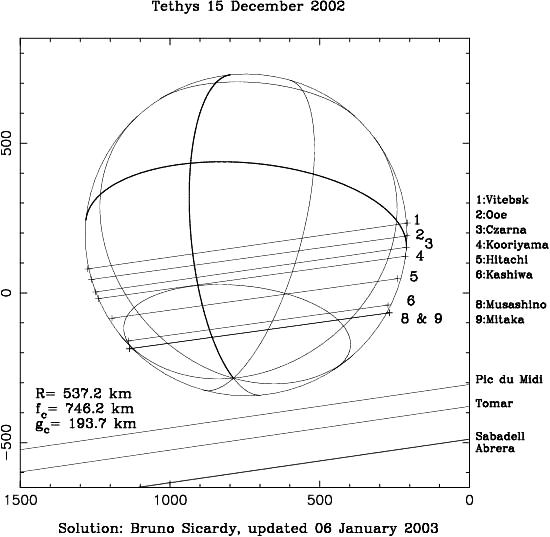
Reconstitution de la figure (=profil) de Tethys, satellite de Saturne, suite aux multiples observations de l'occultation du 15 décembre 2002.
Crédit :
Observatoire de Paris
 Objectifs
Objectifs
Montrer comment une occultation conduit, entre autres, à des mesures inaccessibles par ailleurs : taille et forme de l'objet occultant, sondage de son atmosphère...
Les occultations
Les occultations stellaires sont des phénomènes rares qui mettent en jeu
le passage d'une planète ou d'un satellite devant une étoile. Pendant
quelques minutes, il est alors possible de sonder avec une très grande
précision l'atmosphère du corps, s'il en possède une, de détecter ses
anneaux éventuels, ou de mesurer sa taille avec une précision kilométrique.
L'ombre et la pénombre
Une occultation, comme une éclipse, se caractérise par une ombre et une pénombre. La durée de l'ombre dépend essentiellement de la taille de l'objet du système solaire.
La durée de la pénombre dépend du diamètre stellaire (voir en exercice le principe de la mesure, et les échelles de temps associées). Il s'agit là d'une mesure très simple d'une grandeur par ailleurs inaccessible sans interférométrie.
Ombre et pénombre
La taille finie, non nulle, de l'étoile occultée implique une phase de pénombre, durant laquelle le disque stellaire disparaît ou réapparaît peu à peu.

Principe d'une occultation. La durée de la pénombre dépend du diamètre stellaire. La courbe de lumière de l'étoile (en bleu) mesure son flux en fonction du temps.
Crédit :
ASM
 Pénombre
Pénombre
Difficulté : ☆
Temps : 45 min
On cherche à estimer le diamètre angulaire d'une étoile occultée par un astéroïde.
On note 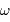 la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire,
la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire, 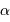 son diamètre angulaire,
son diamètre angulaire, 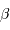 celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
Question 1)
Dans une 1er temps, on fait l'hypothèse que le diamètre angulaire de l'étoile est négligeable. Déterminer la durée 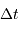 de l'occultation.
de l'occultation.
N'a-t-on pas 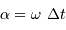 , par définition des variables ?
, par définition des variables ?
Question 2)
On ne suppose plus 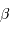 nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates
nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates 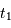 ...
... 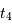 des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
A quoi correspond la phase de pénombre ?
Quelle distance angulaire le satellite a-t-il parcouru durant l'occultation ?
Question 3)
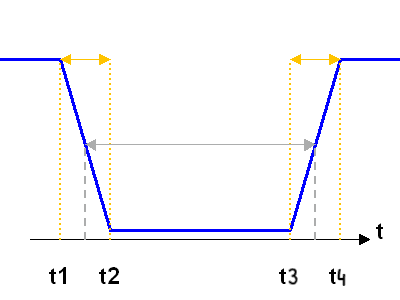
Tracer l'allure de la courbe d'occultation.
Question 4)
A quelle condition peut-on mesurer les diamètres angulaire et linéaire de l'objet, de l'étoile ?
Déterminer les inconnues et les observables : vitesse angulaire, distances...
Question 5)
Les objets du système solaire ont typiquement une vitesse angulaire, notée en "/h, de 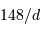 , avec
, avec 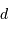 leur distance au soleil exprimée en UA.
La distance
leur distance au soleil exprimée en UA.
La distance 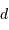 a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
Il suffit de procéder dans l'ordre, et de calculer la vitesse angulaire, le rayon angulaire... ou de simplifier les calculs en prenant garde aux unités !
Question 6)
Chaque phase de pénombre a duré 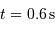 . En déduire le diamètre stellaire, l'étoile étant à
. En déduire le diamètre stellaire, l'étoile étant à 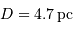 . Comparer le rayon stellaire calculé au rayon solaire.
. Comparer le rayon stellaire calculé au rayon solaire.
Obtenir d'abord le diamètre angulaire de l'étoile.
Pour passer du diamètre angulaire de l'étoile à son diamètre linéaire, appliquer directement la définition du parsec.
- Question 1
Aide :
N'a-t-on pas 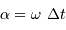 , par définition des variables ?
, par définition des variables ?
Solution :
La relation entre vitesse angulaire et angle conduit à
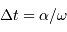 .
.
- Question 2
Aide :
A quoi correspond la phase de pénombre ?
Aide :
Quelle distance angulaire le satellite a-t-il parcouru durant l'occultation ?
Solution :
La phase de pénombre débute au 1er contact entre les 2 objets, jusqu'à ce que l'étoile soit totalement occultée. Cette phase de 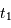 à
à 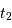 dure
dure 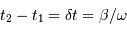 . Par symétrie,
. Par symétrie, 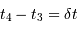 .
.
Lors de la phase de totalité, le satellite parcourt son diamètre moins celui de l'étoile. On a donc : 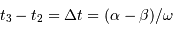 .
.
On en déduit, par rapport à la centralité 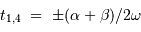 et
et 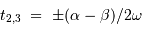 .
.
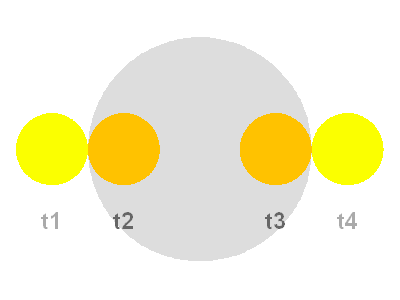
Crédit :
ASM
- Question 3
Solution :
Courbe de lumière de l'occultation. La flèche grise mesure la durée moyenne.
Crédit :
ASM
- Question 4
Aide :
Déterminer les inconnues et les observables : vitesse angulaire, distances...
Solution :
La vitesse angulaire 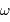 de l'objet est mesurable : les diamètres angulaires
de l'objet est mesurable : les diamètres angulaires 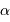 et
et 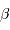 sont alors déterminés par les mesures de
sont alors déterminés par les mesures de 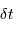 et
et 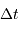 .
.
La distance au soleil de l'objet occultant peut être déduite, par application des lois de la gravitation, de son mouvement.
La mesure du diamètre linéaire de l'objet ou de l'étoile va dépendre de sa distance 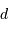 :
:
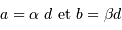
- Question 5
Aide :
Il suffit de procéder dans l'ordre, et de calculer la vitesse angulaire, le rayon angulaire... ou de simplifier les calculs en prenant garde aux unités !
Solution :
Avec une vitesse angulaire 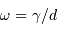 ,
, 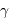 s'exprimant en UA."/h, le diamètre angulaire s'écrit
s'exprimant en UA."/h, le diamètre angulaire s'écrit
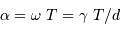 (AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de
(AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de 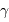 ).
).
Le diamètre linéaire 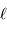 vérifie
vérifie 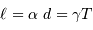 . L'application numérique donne
. L'application numérique donne 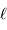 en UA."
en UA."
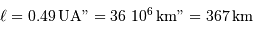 .
.
- Question 6
Aide :
Obtenir d'abord le diamètre angulaire de l'étoile.
Aide :
Pour passer du diamètre angulaire de l'étoile à son diamètre linéaire, appliquer directement la définition du parsec.
Solution :
Par règle de 3 entre les durées et les distances angulaires, le diamètre angulaire vaut :
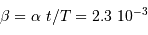 seconde d'arc.
seconde d'arc.
Passer du diamètre angulaire de l'étoile (donné en seconde d'arc) et de la distance (donnée en parsec) au diamètre linéaire de l'étoile par la définition du parsec donne le résultat simplement en UA.
A 4.7 pc, ce diamètre angulaire correspond à un diamètre linéaire 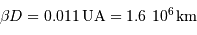 , très proche du diamètre du Soleil (1.4 millions de km).
, très proche du diamètre du Soleil (1.4 millions de km).
Remarquer que les durées à mesurer sont courtes.



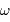 la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire,
la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire, 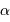 son diamètre angulaire,
son diamètre angulaire, 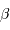 celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
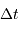 de l'occultation.
de l'occultation.
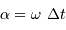 , par définition des variables ?
, par définition des variables ?
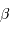 nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates
nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates 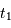 ...
... 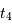 des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
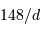 , avec
, avec 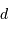 leur distance au soleil exprimée en UA.
La distance
leur distance au soleil exprimée en UA.
La distance 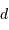 a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
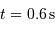 . En déduire le diamètre stellaire, l'étoile étant à
. En déduire le diamètre stellaire, l'étoile étant à 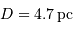 . Comparer le rayon stellaire calculé au rayon solaire.
. Comparer le rayon stellaire calculé au rayon solaire.
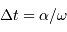 .
.
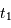 à
à 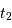 dure
dure 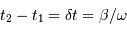 . Par symétrie,
. Par symétrie, 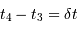 .
.
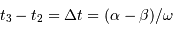 .
.
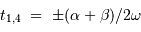 et
et 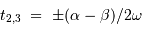 .
.


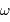 de l'objet est mesurable : les diamètres angulaires
de l'objet est mesurable : les diamètres angulaires 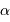 et
et 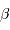 sont alors déterminés par les mesures de
sont alors déterminés par les mesures de 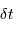 et
et 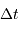 .
.
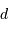 :
:
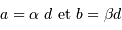
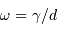 ,
, 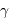 s'exprimant en UA."/h, le diamètre angulaire s'écrit
s'exprimant en UA."/h, le diamètre angulaire s'écrit
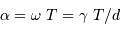 (AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de
(AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de 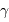 ).
).
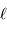 vérifie
vérifie 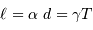 . L'application numérique donne
. L'application numérique donne 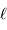 en UA."
en UA."
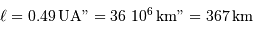 .
.
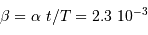 seconde d'arc.
seconde d'arc.
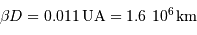 , très proche du diamètre du Soleil (1.4 millions de km).
, très proche du diamètre du Soleil (1.4 millions de km).