
 Pénombre
Pénombre
Difficulté : ☆
Temps : 45 min
On cherche à estimer le diamètre angulaire d'une étoile occultée par un astéroïde.
On note 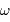 la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire,
la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire, 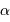 son diamètre angulaire,
son diamètre angulaire, 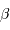 celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
Question 1)
Dans une 1er temps, on fait l'hypothèse que le diamètre angulaire de l'étoile est négligeable. Déterminer la durée 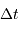 de l'occultation.
de l'occultation.
AideSolution
N'a-t-on pas 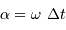 , par définition des variables ?
, par définition des variables ?
La relation entre vitesse angulaire et angle conduit à
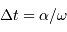 .
.
Question 2)
On ne suppose plus 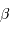 nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates
nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates 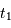 ...
...  des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
AideAideSolution
A quoi correspond la phase de pénombre ?
Quelle distance angulaire le satellite a-t-il parcouru durant l'occultation ?
Question 3)
Tracer l'allure de la courbe d'occultation.
Solution
Courbe de lumière de l'occultation. La flèche grise mesure la durée moyenne.
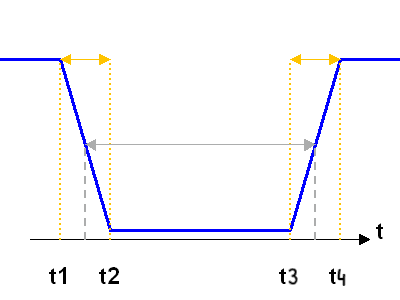
Crédit :
ASM
Question 4)
A quelle condition peut-on mesurer les diamètres angulaire et linéaire de l'objet, de l'étoile ?
AideSolution
Déterminer les inconnues et les observables : vitesse angulaire, distances...
Question 5)
Les objets du système solaire ont typiquement une vitesse angulaire, notée en "/h, de 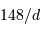 , avec
, avec 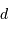 leur distance au soleil exprimée en UA.
La distance
leur distance au soleil exprimée en UA.
La distance 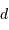 a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
AideSolution
Il suffit de procéder dans l'ordre, et de calculer la vitesse angulaire, le rayon angulaire... ou de simplifier les calculs en prenant garde aux unités !
Question 6)
Chaque phase de pénombre a duré 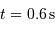 . En déduire le diamètre stellaire, l'étoile étant à
. En déduire le diamètre stellaire, l'étoile étant à 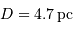 . Comparer le rayon stellaire calculé au rayon solaire.
. Comparer le rayon stellaire calculé au rayon solaire.
AideAideSolution
Obtenir d'abord le diamètre angulaire de l'étoile.
Pour passer du diamètre angulaire de l'étoile à son diamètre linéaire, appliquer directement la définition du parsec.
Par règle de 3 entre les durées et les distances angulaires, le diamètre angulaire vaut :
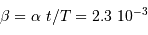 seconde d'arc.
seconde d'arc.
Passer du diamètre angulaire de l'étoile (donné en seconde d'arc) et de la distance (donnée en parsec) au diamètre linéaire de l'étoile par la définition du parsec donne le résultat simplement en UA.
A 4.7 pc, ce diamètre angulaire correspond à un diamètre linéaire 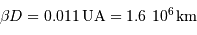 , très proche du diamètre du Soleil (1.4 millions de km).
, très proche du diamètre du Soleil (1.4 millions de km).
Remarquer que les durées à mesurer sont courtes.

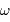 la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire,
la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire, 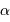 son diamètre angulaire,
son diamètre angulaire, 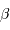 celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
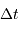 de l'occultation.
de l'occultation.
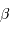 nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates
nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates 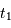 ...
... 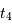 des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
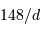 , avec
, avec 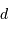 leur distance au soleil exprimée en UA.
La distance
leur distance au soleil exprimée en UA.
La distance 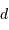 a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.