
Amas Messier 35 et NGC2158. Tous deux sont des amas ouverts, mais l'un, âgé de 100 millions d'années, présente beaucoup d'étoiles jeunes, lorsque, 6 fois plus distant et 10 fois plus âgé, ne peut plus contenir d'étoiles jeunes.
Crédit :
CFHT
Système lié
L'observation de groupes stellaires formant apparemment un
système lié semble indiquer une origine commune. L'estimation des
énergies cinétique et potentielle permet d'estimer l'énergie
mécanique totale. Si les termes cinétiques dominent, l'amas est
ouvert.
 Objectifs
Objectifs
Mesurer l'énergie que représente l'accrétion d'un corps dense.
Analyse dimensionnelle
On s'intéresse à un corps autogravitant de masse 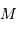 et rayon
et rayon 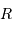 . Quelle énergie peut-on lui associer de par sa gravitation ?
. Quelle énergie peut-on lui associer de par sa gravitation ?
L'analyse dimensionnelle apporte une première réponse à cette question. Avec les caractéristiques de l'objet et la constante gravitationnelle 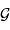 :
:
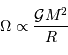
Pour s'en convaincre, il suffit de revenir à la définition de l'interaction gravitationnelle.
Énergie potentielle d'interaction gravitationnelle
Avec un peu de physique, on peut se convaincre d'un supplément d'information :
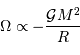
L'interaction en jeu étant attractive, nécessairement l'énergie associée à un corps dense est négative : en effet, pour défaire ce corps, il faudrait lui fournir un travail positif, pour éparpiller très loin chacune de ses particules.
L'énergie potentielle d'interaction gravitationnelle d'un objet est d'autant plus négative qu'il est massif et/ou condensé.
Le calcul complet de cette énergie potentielle est proposé en exercice.
 Calcul de l'énergie potentielle
Calcul de l'énergie potentielle
Difficulté : ☆☆☆
Temps : 45 min
Cet exercice un peu technique s'adresse surtout aux étudiants en licence ou maîtrise scientifique ; sinon, se contenter de suivre l'approche qualitative.
L'exercice s'attelle à la construction d'un objet stellaire. On part de rien. On y met un chouïa de matière, puis un peu plus, puis encore plus, jusqu'à constituer un corps de rayon 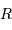 et masse
et masse 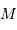 . Dans cette modélisation, on suppose qu'à tout moment la masse volumique
. Dans cette modélisation, on suppose qu'à tout moment la masse volumique 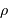 est uniforme.
est uniforme.
Question 1)
On imagine être à une étape intermédiaire caractérisée par un rayon 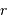 et une masse
et une masse 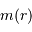 . Déterminer cette masse, ainsi que son champ gravitationnel.
. Déterminer cette masse, ainsi que son champ gravitationnel.
[2 points]
Rappel : la masse volumique est supposée uniforme.
Question 2)
Déterminer le travail d'un opérateur qui amènerait un surcroît de
masse 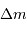 depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
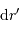 ):
):
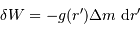
[2 points]
Le travail total est la somme des contributions des travaux de l'infini à la surface de l'objet
Question 4)
En déduire le travail total pour créer le corps, somme de toutes les contributions.
[2 points]
- Question 1
Aide :
Rappel : la masse volumique est supposée uniforme.
Solution :
Par définition :
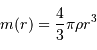
Le champ gravitationnel créé par cette masse à une distance 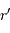 vaut :
vaut :
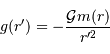
Le signe négatif rend compte de l'attraction gravitationnelle, et il faut bien distinguer les variables 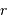 , rayon actuel de l'objet en cours de formation, et
, rayon actuel de l'objet en cours de formation, et 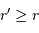 , distance à cet objet.
, distance à cet objet.
- Question 2
Aide :
Le travail total est la somme des contributions des travaux de l'infini à la surface de l'objet
Solution :
À partir d'une étape élémentaire, on somme pour obtenir le travail
total :
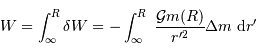
L'intégration donne :
![W = + \left[ { {\cal G} m(M) \over r'}\ \Delta m \right]_\infty^R](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation20.png)
On en tire
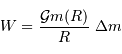
Le travail de l'opérateur est l'opposé de la variation d'énergie potentielle de l'objet entre les 2 états considérés.
- Question 3
Aide :
2 moyens de procéder au calcul, en interprétant l'usage de la notation différentielle, ou bien en raisonnant géométriquement.
Aide :
L'usage de la notation différentielle doit permettre de passer de 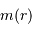 à
à 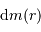 .
.
Solution :
L'accroissement de la masse 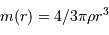 s'écrit par différentiation :
s'écrit par différentiation :
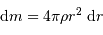
on y reconnaît la masse d'une coquille d'épaisseur 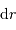 et de surface
et de surface 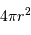 .
.
On a donc :
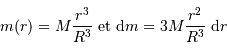
- Question 4
Solution :
De l'expression du travail élémentaire qui précède, on tire l'expression de la variation d'énergie potentielle d'interaction gravitationnelle sur une étape élémentaire :
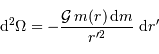
Avec 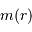 la masse accrétée au rayon
la masse accrétée au rayon 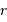 et
et 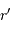 une position entre
une position entre 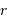 et
et 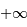 . Une première étape d'intégration conduit à apporter la masse
. Une première étape d'intégration conduit à apporter la masse 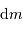 de l'infini à la surface :
de l'infini à la surface :
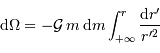
Le calcul de l'intégrale donne ![\left[ - \displaystyle{1\over r'}\right]_\infty^r = - \displaystyle{1\over r}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation46.png) . D'où la variation de potentiel :
. D'où la variation de potentiel :
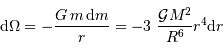
après avoir remplacé 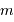 et
et 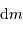 par leur valeurs.
Et donc finalement :
par leur valeurs.
Et donc finalement :
![\Omega = \int_0^R {\mathrm{d}} \Omega = \left[ - 3 { {\cal G} M^2\over R^6} {r^5\over 5} \right]_0^R = -{3\over 5} { {\cal G} M^2\over R}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation50.png)
On retrouve ce résultat classique. L'expression est homogène ; le signe négatif rappelle que la formation d'une concentration de matière a dégagé de l'énergie (ou qu'il faut en dépenser pour démonter l'objet).

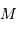 et rayon
et rayon 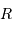 . Quelle énergie peut-on lui associer de par sa gravitation ?
. Quelle énergie peut-on lui associer de par sa gravitation ?
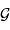 :
:
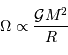
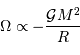
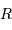 et masse
et masse 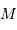 . Dans cette modélisation, on suppose qu'à tout moment la masse volumique
. Dans cette modélisation, on suppose qu'à tout moment la masse volumique 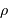 est uniforme.
est uniforme.
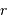 et une masse
et une masse 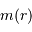 . Déterminer cette masse, ainsi que son champ gravitationnel.
. Déterminer cette masse, ainsi que son champ gravitationnel.
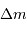 depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
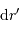 ):
):
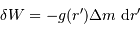
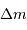 sert à construire l'objet. L'exprimer en fonction de l'accroissement de rayon
sert à construire l'objet. L'exprimer en fonction de l'accroissement de rayon 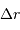 . Pour simplifier, on suppose ces 2 grandeurs petites, et l'on utilise en conséquence la notation différentielle
. Pour simplifier, on suppose ces 2 grandeurs petites, et l'on utilise en conséquence la notation différentielle 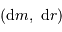 . Exprimer alors
. Exprimer alors 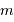 et
et 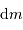 en fonction de la masse totale finale
en fonction de la masse totale finale 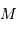 , des rayons
, des rayons 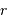 et
et 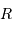 , et l'accroissement
, et l'accroissement 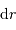 .
.
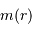 à
à 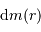 .
.
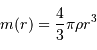
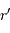 vaut :
vaut :
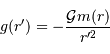
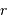 , rayon actuel de l'objet en cours de formation, et
, rayon actuel de l'objet en cours de formation, et 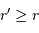 , distance à cet objet.
, distance à cet objet.
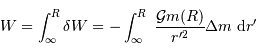
![W = + \left[ { {\cal G} m(M) \over r'}\ \Delta m \right]_\infty^R](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation20.png)
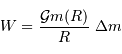
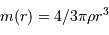 s'écrit par différentiation :
s'écrit par différentiation :
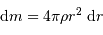
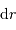 et de surface
et de surface 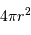 .
.
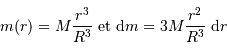
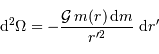
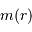 la masse accrétée au rayon
la masse accrétée au rayon 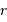 et
et 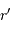 une position entre
une position entre 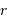 et
et 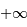 . Une première étape d'intégration conduit à apporter la masse
. Une première étape d'intégration conduit à apporter la masse 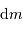 de l'infini à la surface :
de l'infini à la surface :
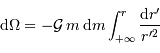
![\left[ - \displaystyle{1\over r'}\right]_\infty^r = - \displaystyle{1\over r}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation46.png) . D'où la variation de potentiel :
. D'où la variation de potentiel :
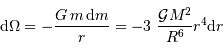
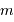 et
et 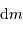 par leur valeurs.
Et donc finalement :
par leur valeurs.
Et donc finalement :
![\Omega = \int_0^R {\mathrm{d}} \Omega = \left[ - 3 { {\cal G} M^2\over R^6} {r^5\over 5} \right]_0^R = -{3\over 5} { {\cal G} M^2\over R}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation50.png)