S'exercer

Calcul de l'énergie potentielle

Difficulté : ☆☆☆ Temps : 45 min

Cet exercice un peu technique s'adresse surtout aux étudiants en licence ou maîtrise scientifique ; sinon, se contenter de suivre l'approche qualitative.

L'exercice s'attelle à la construction d'un objet stellaire. On part de rien. On y met un chouïa de matière, puis un peu plus, puis encore plus, jusqu'à constituer un corps de rayon 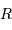et masse 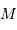. Dans cette modélisation, on suppose qu'à tout moment la masse volumique 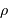$\rho$ est uniforme.

Question 1)

On imagine être à une étape intermédiaire caractérisée par un rayon 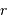et une masse 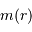m(r) . Déterminer cette masse, ainsi que son champ gravitationnel.

Aide Solution [2 points]

Question 2)

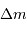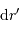Déterminer le travail d'un opérateur qui amènerait un surcroît de masse $\Delta m$ depuis l'infini jusqu'à la surface de cet objet. On définit ce travail par une étape élémentaire (déplacement ${\mathrm{d}} r'$ ):

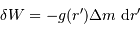
$\delta W = - g(r') \Delta m \ {\mathrm{d}} r'$

Aide Solution [2 points]

Question 3)

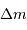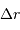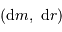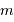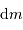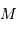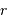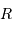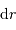Cette masse $\Delta m$ sert à construire l'objet. L'exprimer en fonction de l'accroissement de rayon $\Delta r$ . Pour simplifier, on suppose ces 2 grandeurs petites, et l'on utilise en conséquence la notation différentielle $( {\mathrm{d}} m, \ {\mathrm{d}} r)$ . Exprimer alors et ${\mathrm{d}} m$ en fonction de la masse totale finale , des rayons et , et l'accroissement ${\mathrm{d}} r$ .

Aide Aide Solution [2 points]

Question 4)

En déduire le travail total pour créer le corps, somme de toutes les contributions.

Solution [2 points]