Apprendre

Objectifs

Mesurer l'énergie que représente l'accrétion d'un corps dense.

Analyse dimensionnelle

On s'intéresse à un corps autogravitant de masse 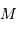et rayon 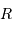. Quelle énergie peut-on lui associer de par sa gravitation ?

L'analyse dimensionnelle apporte une première réponse à cette question. Avec les caractéristiques de l'objet et la constante gravitationnelle 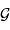${\cal G}$ :

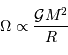
$\Omega \propto { {\cal G} M^2 \over R}$

Pour s'en convaincre, il suffit de revenir à la définition de l'interaction gravitationnelle.

Énergie potentielle d'interaction gravitationnelle

Avec un peu de physique, on peut se convaincre d'un supplément d'information :

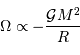
$\Omega \propto - { {\cal G} M^2 \over R}$

L'interaction en jeu étant attractive, nécessairement l'énergie associée à un corps dense est négative : en effet, pour défaire ce corps, il faudrait lui fournir un travail positif, pour éparpiller très loin chacune de ses particules.

L'énergie potentielle d'interaction gravitationnelle d'un objet est d'autant plus négative qu'il est massif et/ou condensé. Le calcul complet de cette énergie potentielle est proposé en exercice.