Autogravitation et forme sphérique
Une étoile présente une forme sphérique, pas évidente à voir vu la petitesse du rayon stellaire devant la distance entre elle et le Soleil. Le disque stellaire d'une étoile ne peut être imagé que si cette étoile est une géante du proche voisinage solaire.
Un noyau de comète, tel celui de la comète de Halley, n'est pas assez massif pour être façonné par sa propre gravitation. Sa forme n'est pas sphérique.
Atmosphère de Bételgeuse

Atmosphère de l'étoile supergéante rouge Bételgeuse. Cette géante
rouge, de diamètre 800 fois celui du Soleil, est suffisamment
proche (130 pc) pour que son disque puisse être imagé.
Crédit :
HST
Noyau de la comète de Halley

Noyau de la comète de Halley, vue en 1986 par la sonde européenne Giotto, lors d'un survol à 600 km (mais avec une vitesse relative de 70 km/s. Ce noyau cométaire n'est pas assez massif pour acquérir une forme sphérique.
Crédit :
ESA
 Objectifs
Objectifs
Exprimer sous forme d'une pression (la pression centrale) l'autogravitation d'une étoile.
Autogravitation
On qualifie d'autogravitant un objet soumis à sa propre gravitation et façonné par elle. Le Soleil, la Terre sont des objets autogravitants. Toi, lecteur, tu n'es pas un objet auto-gravitant (tout au plus sujet à un peu d'embonpoint).
Rien n'interdit à un objet autogravitant de graviter autour d'un autre astre, comme la Terre autour du Soleil ou la Lune autour de la Terre.
Un objet autogravitant est de forme sphérique si sa rotation propre n'est pas trop importante, ou ovoïde aplatie dans le cas contraire.
Équilibre
Comme cette pression rend compte de l'interaction gravitationnelle, attractive, on l'appellera par la suite compression. Il va falloir lui trouver, au sein d'un astre, une contrepartie répulsive pour assurer l'équilibre d'une étoile.
Rotation et aplatissement
La rotation de Saturne est suffisamment rapide pour conduire à un aplatissement sensible.
Le mesurer à l'aide de l'appliquette ci-contre, en déterminant le rapport 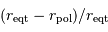 .
.
Montrer que l'inclinaison sous laquelle on voit la planète, estimée à partir des anneaux, ne perturbe pas significativement la mesure précédente.
Saturne 
 Compression gravitationnelle
Compression gravitationnelle
Difficulté : ☆☆☆
Temps : 30 min
Le but de l'exercice est d'estimer la constante de proportionnalité de la compression gravitationnelle. Pour dépasser l'approximation d'une masse volumique uniforme, et rendre compte d'une distribution de masse volumique plus piquée vers le centre, tout en gardant des calculs acceptablement légers, on suppose le modèle suivant :
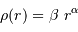 .
.
On s'intéresse à des exposants légèrement négatifs, conduisant à une singularité au centre, qui ne prête pas à conséquence.
Question 1)
Déterminer la relation entre la masse totale 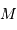 et le rayon extérieur
et le rayon extérieur 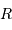 . En déduire l'expression du coefficient
. En déduire l'expression du coefficient 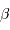 en fonction de ces grandeurs.
en fonction de ces grandeurs.
[2 points]
Pour cette distribution sphérique :
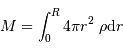
Question 2)
En déduire la masse 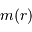 et le champ gravitationnel en un point de rayon
et le champ gravitationnel en un point de rayon 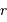 . Quelle condition sur l'exposant
. Quelle condition sur l'exposant 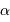 garantit que le champ ne diverge pas ?
garantit que le champ ne diverge pas ?
[2 points]
Pour des calculs plus simples, on écrit :
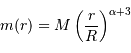
Par définition :
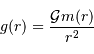
Question 3)
L'équilibre hydrostatique donne le gradient de pression :
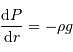
En déduire la pression centrale.
[2 points]
Mener le calcul, du centre vers la surface :
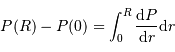
Question 4)
Discuter de la forme du résultat précédent. Que se passe-t-il pour une distribution uniforme ?
[1 points]
Traduire l'uniformité de la masse volumique sur l'exposant 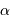 .
.
Est-il normal de retrouver 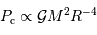 ?
?
 Ainsi fond, fond, fond...
Ainsi fond, fond, fond...
Difficulté : ☆☆
Temps : 30 min
Limbe lunaire : la hauteur des plus hauts reliefs reste petite devant le rayon.

Relief sur le limbe lunaire.
Crédit :
ASM
Le but de cet exercice est de modéliser la hauteur limite d'une montagne sur une planète de masse 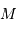 et rayon
et rayon 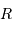 , pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
, pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
On suppose très hardiment la montagne de forme cylindrique, section 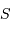 et hauteur
et hauteur 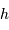 , dans le champ gravitationnel uniforme de la planète.
, dans le champ gravitationnel uniforme de la planète.
Question 2)
En déduire la valeur limite de la hauteur 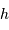 , pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches
, pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches 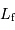 . Faire l'application numérique pour la Terre, avec
. Faire l'application numérique pour la Terre, avec 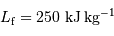 .
.
[2 points]
Comparer les énergies en jeu.
Question 3)
Les plus hautes montagnes atteignent 8.8 km sur Terre (l'Everest) et 27 sur Mars (le Mont Olympe). A l'aide des données du calcotron, vérifier si l'estimation précédente est correcte.
[1 points]
Question 4)
En supposant toujours valable le résultat précédent, et en notant 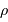 la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de
la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de 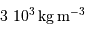 .
.
[2 points]
Ne pas se laisser désarçonner par les hypothèses, qui restent en ordre de grandeur très convenables.
- Question 1
Aide :
Pour cette distribution sphérique :
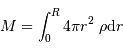
Solution :
Par application de la définition de la masse totale :
![M = \int_0^R 4\pi r^2\ \rho {\mathrm{d}} r = 4\pi \beta \ \int_0^R r^{\alpha+2} {\mathrm{d}} r = 4\pi \beta \ \left[ {r^{\alpha+3}\over \alpha+3} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation27.png)
Si 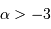 , alors :
, alors :
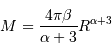
D'où l'expression demandée :
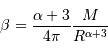
- Question 2
Aide :
Pour des calculs plus simples, on écrit :
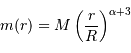
Aide :
Par définition :
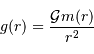
Solution :
De l'expression de la masse totale trouvée précédemment, on peut déduire de la même façon :
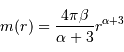
(seule la borne d'intégration supérieure a changé). On en déduit :
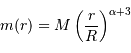
Ensuite, la définition du champ gravitationnel donne :
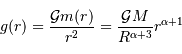
Il semble nécessaire d'avoir un exposant 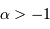 , afin d'éviter que le champ ne diverge au centre.
, afin d'éviter que le champ ne diverge au centre.
- Question 3
Aide :
Mener le calcul, du centre vers la surface :
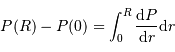
Solution :
On cherche à intégrer la pression du centre 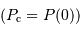 vers la surface
vers la surface 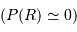 :
:
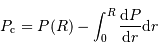
On suppose la pression de surface totalement négligeable. Il reste alors, en fonction de ce qui précède :
![P _{\mathrm{c}} = \int_0^R \rho g\ {\mathrm{d}} r = \int_0^R \beta r^\alpha \ { {\cal G} M \over R^{\alpha+3}} r^{\alpha+1} {\mathrm{d}} r = \beta { {\cal G} M \over R^{\alpha+3}} \int_0^R r^{2\alpha+1} {\mathrm{d}} r = {\alpha+3 \over 4\pi}\ { {\cal G} M^2 \over R^{2\alpha+6}} \left[ {r^{2\alpha+2}\over 2\alpha+2} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation45.png)
L'expression du champ a conduit à la restriction 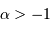 ; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
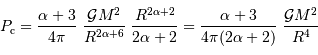
- Question 4
Aide :
Traduire l'uniformité de la masse volumique sur l'exposant 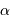 .
.
Aide :
Est-il normal de retrouver 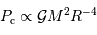 ?
?
Solution :
Retrouver 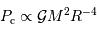 est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel
est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel 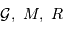 .
.
Si la masse volumique est uniforme, c'est à dire si 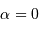 , on trouve :
, on trouve :
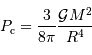
Si la masse volumique pointe vers le centre, c'est àdire 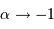 , on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la partie cours, dans le cas du Soleil.
, on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la partie cours, dans le cas du Soleil.
- Question 1
Aide :
Le champ gravitationnel vaut 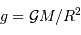 .
.
Solution :
Monter d'une hauteur 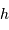 la masse considérée coûte en énergie, dans le champ
la masse considérée coûte en énergie, dans le champ 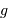 supposé uniforme :
supposé uniforme :
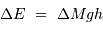
- Question 2
Aide :
Comparer les énergies en jeu.
Solution :
L'énergie gravitationnelle comparée à l'énergie de fusion montre que la dépense énergétique peut faire fondre la base si
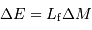 , et donc si :
, et donc si :
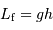
AN: 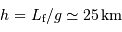
- Question 3
Solution :
A un facteur 3 près, ça semble se tenir.
- Question 4
Aide :
Ne pas se laisser désarçonner par les hypothèses, qui restent en ordre de grandeur très convenables.
Solution :
L'égalité dans le cas limite, 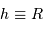 , et la définition de la masse pour une masse volumique uniforme
, et la définition de la masse pour une masse volumique uniforme
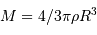 conduisent à :
conduisent à :
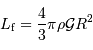
soit
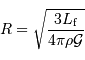
AN : 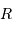 de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.


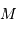 et rayon
et rayon 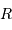 . Elle vaut :
. Elle vaut :
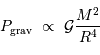
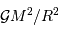 étant homogène à une force.
étant homogène à une force.
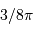 ; comme vérifié en
; comme vérifié en 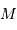 (kg)
(kg)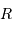 (km)
(km) 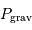 (Pa)
(Pa)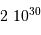
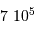
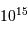
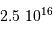
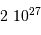
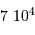
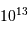
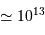
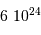
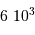
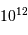
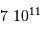
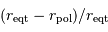 .
.

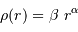 .
.
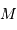 et le rayon extérieur
et le rayon extérieur 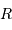 . En déduire l'expression du coefficient
. En déduire l'expression du coefficient 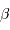 en fonction de ces grandeurs.
en fonction de ces grandeurs.
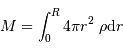
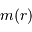 et le champ gravitationnel en un point de rayon
et le champ gravitationnel en un point de rayon 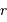 . Quelle condition sur l'exposant
. Quelle condition sur l'exposant 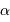 garantit que le champ ne diverge pas ?
garantit que le champ ne diverge pas ?
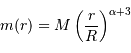
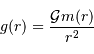
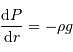
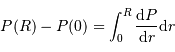
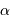 .
.
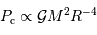 ?
?

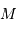 et rayon
et rayon 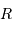 , pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
, pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
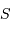 et hauteur
et hauteur 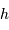 , dans le champ gravitationnel uniforme de la planète.
, dans le champ gravitationnel uniforme de la planète.
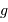 . Déterminer l'énergie supplémentaire pour rajouter au sommet une masse
. Déterminer l'énergie supplémentaire pour rajouter au sommet une masse 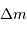 , en fonction de
, en fonction de 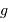 et
et 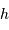 .
.
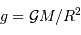 .
.
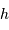 , pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches
, pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches 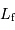 . Faire l'application numérique pour la Terre, avec
. Faire l'application numérique pour la Terre, avec 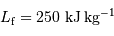 .
.
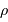 la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de
la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de 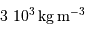 .
.
![M = \int_0^R 4\pi r^2\ \rho {\mathrm{d}} r = 4\pi \beta \ \int_0^R r^{\alpha+2} {\mathrm{d}} r = 4\pi \beta \ \left[ {r^{\alpha+3}\over \alpha+3} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation27.png)
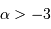 , alors :
, alors :
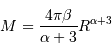
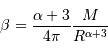
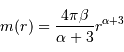
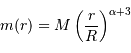
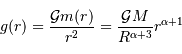
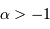 , afin d'éviter que le champ ne diverge au centre.
, afin d'éviter que le champ ne diverge au centre.
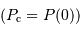 vers la surface
vers la surface 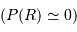 :
:
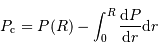
![P _{\mathrm{c}} = \int_0^R \rho g\ {\mathrm{d}} r = \int_0^R \beta r^\alpha \ { {\cal G} M \over R^{\alpha+3}} r^{\alpha+1} {\mathrm{d}} r = \beta { {\cal G} M \over R^{\alpha+3}} \int_0^R r^{2\alpha+1} {\mathrm{d}} r = {\alpha+3 \over 4\pi}\ { {\cal G} M^2 \over R^{2\alpha+6}} \left[ {r^{2\alpha+2}\over 2\alpha+2} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation45.png)
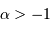 ; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
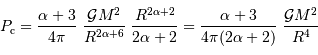
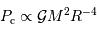 est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel
est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel 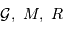 .
.
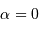 , on trouve :
, on trouve :
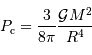
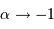 , on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la
, on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la 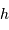 la masse considérée coûte en énergie, dans le champ
la masse considérée coûte en énergie, dans le champ 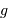 supposé uniforme :
supposé uniforme :
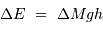
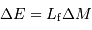 , et donc si :
, et donc si :
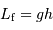
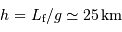
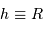 , et la définition de la masse pour une masse volumique uniforme
, et la définition de la masse pour une masse volumique uniforme
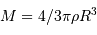 conduisent à :
conduisent à :
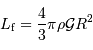
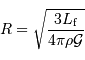
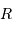 de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.