 |  |  |  |  |  |
|
Compression gravitationnelleDifficulté : ☆☆☆ Temps : 30 min
Le but de l'exercice est d'estimer la constante de proportionnalité de la compression gravitationnelle. Pour dépasser l'approximation d'une masse volumique uniforme, et rendre compte d'une distribution de masse volumique plus piquée vers le centre, tout en gardant des calculs acceptablement légers, on suppose le modèle suivant :
.
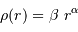On s'intéresse à des exposants légèrement négatifs, conduisant à une singularité au centre, qui ne prête pas à conséquence.
Déterminer la relation entre la masse totale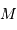 
et le rayon extérieur 
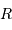. En déduire l'expression du coefficient 
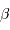en fonction de ces grandeurs.
En déduire la masse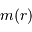 
et le champ gravitationnel en un point de rayon 
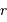. Quelle condition sur l'exposant 
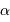garantit que le champ ne diverge pas ?
L'équilibre hydrostatique donne le gradient de pression :
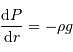
En déduire la pression centrale.
Ainsi fond, fond, fond...Difficulté : ☆☆ Temps : 30 min
Le but de cet exercice est de modéliser la hauteur limite d'une montagne sur une planète de masse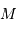 
et rayon 
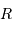, pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
On suppose très hardiment la montagne de forme cylindrique, section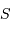 
et hauteur 
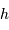, dans le champ gravitationnel uniforme de la planète.
Rappeler l'expression du champ gravitationnel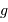 
. Déterminer l'énergie supplémentaire pour rajouter au sommet une masse 
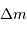, en fonction de 
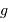et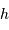 
.
En déduire la valeur limite de la hauteur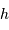 
, pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches 
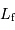. Faire l'application numérique pour la Terre, avec 
.
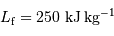Les plus hautes montagnes atteignent 8.8 km sur Terre (l'Everest) et 27 sur Mars (le Mont Olympe). A l'aide des données du calcotron, vérifier si l'estimation précédente est correcte.
Solution [1 points]
En supposant toujours valable le résultat précédent, et en notant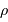 
la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de 
.
 |  |
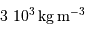S'exercer
![M = \int_0^R 4\pi r^2\ \rho {\mathrm{d}} r = 4\pi \beta \ \int_0^R r^{\alpha+2} {\mathrm{d}} r = 4\pi \beta \ \left[ {r^{\alpha+3}\over \alpha+3} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation27.png)
, alors :
, afin d'éviter que le champ ne diverge au centre.
vers la surface 
:
![P _{\mathrm{c}} = \int_0^R \rho g\ {\mathrm{d}} r = \int_0^R \beta r^\alpha \ { {\cal G} M \over R^{\alpha+3}} r^{\alpha+1} {\mathrm{d}} r = \beta { {\cal G} M \over R^{\alpha+3}} \int_0^R r^{2\alpha+1} {\mathrm{d}} r = {\alpha+3 \over 4\pi}\ { {\cal G} M^2 \over R^{2\alpha+6}} \left[ {r^{2\alpha+2}\over 2\alpha+2} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation45.png)
; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
.
?
est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel 
.
, on trouve :
, on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la 
.
la masse considérée coûte en énergie, dans le champ 
supposé uniforme :
, et donc si :
, et la définition de la masse pour une masse volumique uniforme
conduisent à :
de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.