Apprendre

Prérequis

Notion de gaz parfait.

Objectifs

Une étoile peut exister sous réserve d'être dans un état d'équilibre. La compression d'origine gravitationnelle, qui tend à condenser l'étoile, doit être balancée par une autre source de pression : pression cinétique (ou thermique), pression de dégénérescence (ou quantique), pression de rayonnement.

Pression cinétique

Aussi appelée pression thermique, cette pression est celle du gaz parfait chaud. Dans le cas classique, non relativiste, cette pression s'exprime pour un gaz de masse volumique 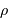$\rho$ à la température 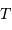, composé de particules de masse :

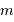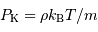
$P _{\mathrm{K}} = \rho k _{\mathrm{B}} T / m$

En fonction de la densité particulaire 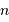, la définition devient :

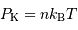
$P _{\mathrm{K}} = n k _{\mathrm{B}} T$

Pression de dégénérescence, ou pression de Fermi, ou pression quantique

La pression de dégénérescence est la pression dans un gaz parfait dit froid. Dans un milieu froid ou dense, les termes cinétiques peuvent devenir négligeables et les interactions entre nuages électroniques des atomes présents prépondérantes. La pression est alors dominée par la pression de dégénérescence 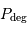$P _{\mathrm{deg}}$ des électrons (s'il y a des électrons). Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.

La pression de dégénérescence s'écrit alors (dans le cas non relativiste) :

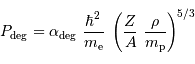
$P _{\mathrm{deg}} = \alpha _{\mathrm{deg}}\ {\hbar^{2}\over m _{\mathrm{e}} }\ \left({Z\over A} \ {\rho\over m _{\mathrm{p}}} \right)^{5/3}$

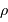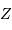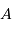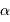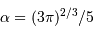avec $\rho$ la masse volumique, et et respectivement la charge et le nombre de masse des atomes en présence. La constante $\alpha$ est un nombre : le calcul précis donne $\alpha = (3\pi)^{2/3} / 5$ .

Dans certains cas, tel l'intérieur d'une étoile à neutrons, il peut ne plus y avoir d'électrons pour assurer la pression. On trouve alors des neutrons, qui sont toujours des fermions, et la pression de dégénérescence des neutrons s'écrit :

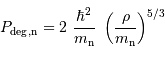
${ P _{\mathrm{deg}}}{} _{\mathrm{, n}} = 2\ {\hbar^{2}\over m _{\mathrm{n}} }\ \left({\rho\over m _{\mathrm{n}}} \right)^{5/3}$

Pression de radiation

La pression de radiation 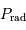$P _{\mathrm{rad}}$ du gaz de photons à la température 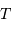s'exprime par :

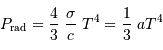
$P _{\mathrm{rad}} = {4\over 3} \ {\sigma\over c} \ T^4 = {1\over 3}\ aT^4$

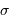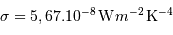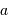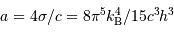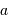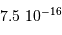où $\sigma$ est la constante de Stefan-Boltzmann : $\sigma = 5,67.10^{-8} {\,\mathrm{W}} {m}^{-2} {\,\mathrm{K}}^{-4}$ . La grandeur s'écrit : $a={4\sigma / c} = {8\pi^5 k _{\mathrm{B}}^4 / 15c^{3} h^{3}}$ . En unité SI, vaut $7.5 \ 10^{-16}$ . La dépendance de cette pression avec la puissance quatrième de la température est bien sûr reliée au spectre du corps noir.

Quel terme de pression domine en fonction de la température ?

La nature est complexe, si bien que ce qui suit n'est pas toujours vrai, mais en général :

Dans un milieu dense et froid, c'est la pression de dégénérescence qui domine. Ex : au centre de la Terre d'une planète, ou d'une étoile de masse inférieure à 1 masse solaire.
Dans un milieu plus chaud, la pression cinétique mène la danse. Par exemple : au centre d'une étoile telle le Soleil ou plus massive. La pression de dégénérescence intervient dans les stades ultimes de l'évolution stellaire.
Ce n'est qu'aux températures extrêmes atteinte au centre des étoiles les plus massives que la pression de radiation l'emporte.

Supporter la gravitation

Dans tous les cas, l'un des 3 termes de pression, ou l'association de 2 d'entre eux, doit permettre d'équilibrer la compression gravitationnelle. Si, on le verra plus loin, la source énergétique essentielle pour l'étoile adulte, dans la séquence principale, est l'énergie nucléaire, c'est la gravitation qui pilote l'évolution stellaire via la masse de l'objet.