 |  |  |  |  |  |
|
Les simulations suivantes donnent, pour une étoile de masse, rayon et température de corps fixés, les valeurs de la température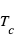 
centrale (en million de Kelvin) et de la masse volumique 
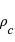centrale (en unité 
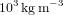). Le but de la simulation est d'estimer le terme de pression dominant au centre de l'étoile, en fonction de sa masse. On mènera les calculs avec des pressions exprimées en unité 1 Gbar (1 milliard de fois la pression atmosphérique, soit 
).
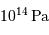Estimer tout d'abord la compression gravitationnelle.
[ 
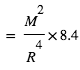] pour avoir la bonne unité
Estimer les termes de pression (avec les constantes numériques pour rattraper la bonne unité de pression ci-dessus définie) :
]
]
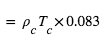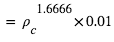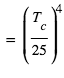]Déterminer l'importance relative des 3 termes de pression. Dans quels cas la pression radiative est-elle négligeable ? Même question pour la pression de dégénérescence.
Montrer que les réservoirs de pression sont suffisants pour contrer la compression gravitationnelle.
 |  |
Simuler