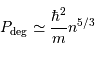Pression de Fermi
Pression de Fermi
Difficulté : ☆☆☆
Temps : 60 min
Cet exercice a pour but d'expliciter l'expression de la pression de Fermi, qui s'exerce lorsque la nature fermionique des composants est mise en évidence. Comme il s'agit de physique complexe, ce sont seulement les ordres de grandeur qui sont importants.
Question 1)
Rappeler la relation d'incertitude de Heisenberg entre la position 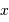 d'une particule sur un axe et sa quantité de mouvement
d'une particule sur un axe et sa quantité de mouvement 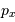 .
.
Solution
[1 points]
La relation de Heisenberg s'écrit, en notant 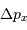 et
et 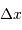 les incertitudes respectives.
les incertitudes respectives.
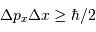
Pour la suite, on considèrera le cas
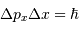
Question 2)
Relier l'incertitude de position 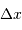 à la densité particulaire
à la densité particulaire 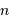 .
.
AideAideSolution
[1 points]
Faire le lien entre la densité particulaire 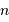 et le volume moyen par particule.
et le volume moyen par particule.
S'intéresser à l'encombrement au sein du gaz, en estimant qu'une particule occupe un volume de l'ordre de 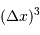 .
.
Question 3)
Montrer que, pour un gaz avec une distribution de vitesse typique, maxwellienne, la distribution de vitesse donne une valeur moyenne et une largeur de distribution du même ordre de grandeur.
AideAideSolution
[1 points]
La distribution de vitesse maxwellienne varie comme
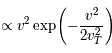 avec
avec 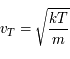
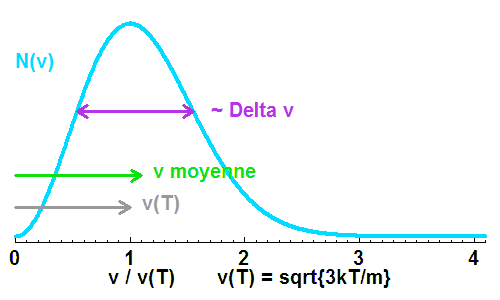
Distribution de vitesse maxwellienne.
Crédit :
ASM
L'examen de la figure montre que vitesse moyenne et écart-type sont du même ordre de grandeur. On confond donc 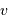 et
et 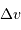 .
.
Question 4)
On rappelle que la pression est un flux de quantité de mouvement
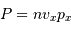
De ce qui précède (en admettant aussi que 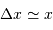 ), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
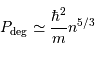
AideAideSolution
[2 points]
Pour un gaz classique : 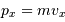 .
.
Éliminer des relations précédentes les variables de quantité de mouvement et de position au profit de la densité particulaire.
Pour un gaz classique, la quantité de mouvement s'écrit 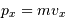 .
.
De 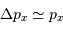 et
et 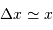 on tire :
on tire :
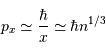
Puis
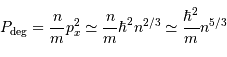
Question 5)
Montrer que la pression électronique domine par rapport à la pression des protons.
AideSolution
[1 points]
Comparer les masses en jeu.
Comme le rapport des masses entre le proton et l'électron vaut 2000, s'il y a des électrons, la pression électronique domine largement.
Question 6)
En déduire l'expression de la pression de dégénérescence donnée dans le
cours.
AideAideSolution
[1 points]
Se servir de la neutralité électrique.
L'essentiel de la masse se retrouve dans les nucléons.
La neutralité électrique assure 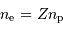 .
.
L'essentiel de la masse se retrouve dans les nucléons : 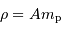 .
.
On retrouve alors le résultat du cours.

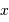 d'une particule sur un axe et sa quantité de mouvement
d'une particule sur un axe et sa quantité de mouvement 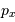 .
.
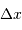 à la densité particulaire
à la densité particulaire 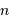 .
.
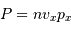
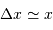 ), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
), montrer que pour un gaz classique la pression de dégénérescence s'écrit :