Fiat lux
La contraction du nuage l'échauffe en son centre, et donc la proto-étoile se met à rayonner. De l'énergie, initialement sous forme uniquement mécanique, a été convertie en énergie lumineuse.

La contraction du nuage l'échauffe en son centre, et donc la proto-étoile se met à rayonner. De l'énergie, initialement sous forme uniquement mécanique, a été convertie en énergie lumineuse.
Par rapport au modèle d'effondrement purement mécanique, il faut tenir compte du rayonnement de la proto-étoile qui s'effondre et s'échauffe. Le théorème du viriel montre que la moitié seulement de l'énergie gagnée par l'effondrement est convertie en énergie thermique, l'autre moitié est directement rayonnée par l'objet condensé qui se réchauffe.
Le modèle étudié précédemment suppose, à juste titre, la conservation de l'énergie, mais à tort que toute cette énergie est sous forme mécanique. Le milieu qui se densifie s'échauffe, et rayonne de l'énergie.
Le théorème du viriel, ici accepté, énonce que l'énergie interne thermique ne représente que la moitié de l'énergie interne gravitationnelle : un bilan énergétique de l'évolution vers un état à l'équilibre hydrostatique implique que la moitié de l'énergie interne est évacuée par radiation.
Lors de la formation d'une étoile, il y a échauffement et
obligatoirement perte d'énergie par radiation, à parts égales :
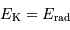 .
.
On peut donc réécrire la loi de conservation de l'énergie :
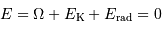
Avec l'égalité entre les énergies rayonnée et cinétique :
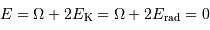
Ceci conduit à une estimation de la température interne de moitié moindre à celle obtenue en omettant l'énergie rayonnée.
La luminosité de l'étoile est reliée au taux de variation de l'énergie rayonnée :
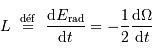
Il s'ensuite que :
De manière plus générale, à tout champ de force correspond une forme particulière du viriel. Pour un champ linéaire (de type ressort), énergies potentielle et cinétique moyennes sont égales. Pour un champ newtonien, elles sont respectivement dans un rapport -2.
Difficulté : ☆☆☆ Temps : 1 h
Cet exercice a pour but d'établir le théorème du viriel, dans un cas simple. On suppose qu'à tout instant, l'astre, sous forme déjà condensée de rayon 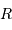 , obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
, obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
Dans le cadre du modèle, avec les notations du cours, on écrit l'énergie cinétique comme une intégrale :
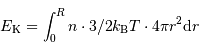 .
Réécrire cette intégrale en fonction de la pression.
.
Réécrire cette intégrale en fonction de la pression.
[1 points]
L'équilibre hydrostatique énonce que le gradient de la pression évolue comme :
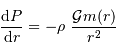
Montrer, à l'aide de cette égalité, que l'énergie gravitationnelle 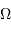 peut s'écrire sous la forme d'une intégrale du gradient de la pression.
peut s'écrire sous la forme d'une intégrale du gradient de la pression.
[3 points]
Estimer le lien entre 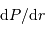 et
et 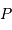 en procédant à l'intégration par parties du terme :
en procédant à l'intégration par parties du terme :
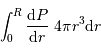
[2 points]
En déduire l'égalité vérifiée entre 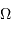 et
et 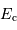 .
.
[2 points]
Difficulté : ☆☆ Temps : 20 min
Le but de cet exercice est d'estimer le rayonnement d'une planète géante encore en train de se contracter. On supposera, dans le cas d'un objet de masse volumique uniforme. L'énergie potentielle est :
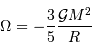
Relier la luminosité de l'objet à sa vitesse de contraction.
[2 points]
Quelle puissance rayonne une planète comme Jupiter qui se contracterait de 1 mm/an ? On donne : 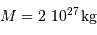 et
et 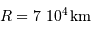 . Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de
. Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de 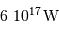 .
.
[1 points]
pages_physique-evolution/theoreme-viriel-sexercer.html
Il suffit d'introduire l'équation d'état du gaz parfait chaud.
Avec l'équation d'état du gaz parfait 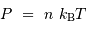 , on introduit simplement la pression, pour obtenir :
, on introduit simplement la pression, pour obtenir :
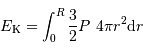
On peut par exemple commencer par écrire l'énergie potentielle sous forme intégrale
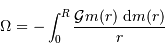
On a aussi besoin de la définition de la masse d'une coquille d'épaisseur 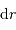 au rayon
au rayon 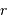 :
:
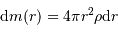
La définition de l'énergie potentielle est :
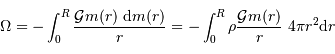
On introduit le gradient de pression, via ce que donne l'équilibre
hydrostatique, sans oublier au passage que 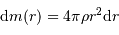 :
:
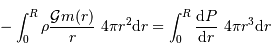
On en déduit :
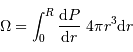
L'intégration par parties donne
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation22.png)
Montrer que l'un des 2 termes de l'intégration par parties est nul.
Par parties :
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation23.png)
Le terme tout intégré est nul, car nul aux 2 bornes (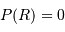 ).
).
Tout le travail est fait, il n'y a plus qu'à comparer.
On a vu pour l'énergie cinétique :
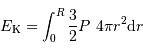
Et pour l'énergie potentielle :
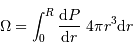
L'égalité trouvée précédemment :
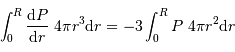
conduit alors à :
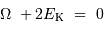
On retrouve donc le théorème du viriel dans un cas particulier.
pages_physique-evolution/theoreme-viriel-sevaluer.html
La vitesse de contraction est 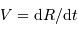 .
.
Par définition, 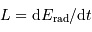 .
.
Le théorème du viriel donne , 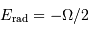 .
.