 Reconstruire la nébuleuse solaire de masse minimale (MMSN)
Reconstruire la nébuleuse solaire de masse minimale (MMSN)
La MMSN est une entité théorique qui permet d’avoir une idée de la structure initiale du disque proto-planétaire qui a formé les planètes du système solaire, en faisant l’hypothèse que celles-ci se sont, en gros, formées à leur emplacement actuel (cf. cours).
A partir de la masse et de la composition actuelle des 8 planètes du système solaire, donner une estimation de la distribution radiale de la matière solide (roches+ glaces) dans la MMSN. Pour cela on peut supposer que la masse solide de toutes les planètes était initialement repartie dans un disque continu s’étendant de l’orbite de Mercure à celle de Neptune. L'information que l'on cherche est alors quelle est la densité surfacique ∑de matière (par exemple en kg/m2) dans ce disque en fonction de la distance radiale r au soleil. Il peut ensuite être intéressant de tracer un graphe représentant ∑(r).
Attention: si pour les planètes telluriques la masse solide de ces planètes peut-être considérée comme étant égale à leur masse totale, il n'en va pas de même pour les planètes géantes (qui contiennent également beaucoup de gaz). La masse totale de matière solide (roche+glaces) contenue dans les planètes géantes n'est pas connue avec une grande précision, mais on pourra prendre les fourchettes suivantes:
Jupiter: entre 10 et 45 MTerre de matière solide
Saturne: entre 20 et 30MTerre de matière solide
Uranus: entre 9 et 13 MTerre de matière solide
Jupiter: entre 12 et 16 MTerre de matière solide
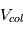 sont de l’ordre des vitesses de libération
sont de l’ordre des vitesses de libération 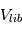 (attention :
(attention : 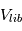 va donc évoluer au cours du temps, car cette vitesse est directement proportionnelle à la taille des planétésimaux)
va donc évoluer au cours du temps, car cette vitesse est directement proportionnelle à la taille des planétésimaux)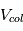 peut alors facilement s’exprimer en fonction de l’excentricité des orbites (voir cours).
peut alors facilement s’exprimer en fonction de l’excentricité des orbites (voir cours).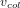 dans un disque d’épaisseur
dans un disque d’épaisseur 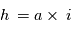 (où a est la distance au soleil eti est l'inclinaison des orbites de tous les planétésimaux)
(où a est la distance au soleil eti est l'inclinaison des orbites de tous les planétésimaux)
![\Sigma_{(0.387UA)}=\frac{3.3\times10^{23}}{\pi\left[\left(8.285\times10^{10}\right)^{2}-\left(2.875\times10^{10}\right)^{2}\right]} = 17.4 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation1.png)
![\Sigma_{(0.723UA)}=\frac{4.87\times10^{24}}{\pi\left[\left(12.5\times10^{10}\right)^{2}-\left(8.285\times10^{10}\right)^{2}\right]} = 175 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation2.png)
![\Sigma_{(1UA)}=\frac{5.972\times10^{24}}{\pi\left[\left(18.87\times10^{10}\right)^{2}-\left(12.5\times10^{10}\right)^{2}\right]} = 95 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation3.png)
![\Sigma_{(1.5UA)}=\frac{6.42\times10^{23}}{\pi\left[\left(33.90\times10^{10}\right)^{2}-\left(18.87\times10^{10}\right)^{2}\right]} = 2.57 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation4.png)
![\Sigma_{(3UA)}=\frac{10^{22}}{\pi\left[\left(61.5\times10^{10}\right)^{2}-\left(33.90\times10^{10}\right)^{2}\right]} = 0.012 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation5.png)
![\Sigma_{(5.2UA)}=\frac{1.80\times10^{26}}{\pi\left[\left(110.5\times10^{10}\right)^{2}-\left(61.5\times10^{10}\right)^{2}\right]} = 67.9 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation6.png)
![\Sigma_{(9.5UA)}=\frac{1.50\times10^{26}}{\pi\left[\left(215.8\times10^{10}\right)^{2}-\left(110.5\times10^{10}\right)^{2}\right]} = 14.0 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation7.png)
![\Sigma_{(19UA)}=\frac{6.6\times10^{25}}{\pi\left[\left(369.4\times10^{10}\right)^{2}-\left(215.8\times10^{10}\right)^{2}\right]} = 2.33 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation8.png)
![\Sigma_{(30UA)}=\frac{8.4\times10^{25}}{\pi\left[\left(525.4\times10^{10}\right)^{2}-\left(369.4\times10^{10}\right)^{2}\right]} = 1.91 kg/m^{2}](../pages_planetologie-formation/equations_formation-setester2/equation9.png)
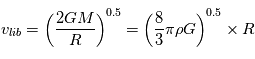
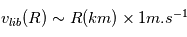
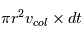 .
Il faut maintenant estimer le nombre de planétésimaux contenus en moyenne dans ce volume.
Ce nombre est donné par
.
Il faut maintenant estimer le nombre de planétésimaux contenus en moyenne dans ce volume.
Ce nombre est donné par 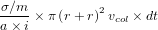 (m étant
la masse d'un planétésimal). Le terme en (r + r)2 vient du fait que
même des corps dont le centre n'est pas dans le volume balayé par le planétésimal considéré
peuvent être impactés par lui en raison de leur taille non-nulle r.
En remplaçant vcol par e.vKep, e/i par 2 et
m par 4/3
(m étant
la masse d'un planétésimal). Le terme en (r + r)2 vient du fait que
même des corps dont le centre n'est pas dans le volume balayé par le planétésimal considéré
peuvent être impactés par lui en raison de leur taille non-nulle r.
En remplaçant vcol par e.vKep, e/i par 2 et
m par 4/3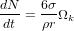 , où
, où 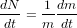 , ce qui donne, en remplaçant dN/dt par la formule précédente et (1/m)*(dm/dt) par (3/r)*(dr/dt), la formule
, ce qui donne, en remplaçant dN/dt par la formule précédente et (1/m)*(dm/dt) par (3/r)*(dr/dt), la formule 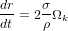 .
On remarque que cette formule très simple ne dépend ni de e, ni de i,
ni de la taille des planétésimaux.
Et, à 1UA, cela donne un taux de croissance
.
On remarque que cette formule très simple ne dépend ni de e, ni de i,
ni de la taille des planétésimaux.
Et, à 1UA, cela donne un taux de croissance 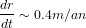 , soit environ 2.5 millions d'années pour
former un corps de 1000km.
, soit environ 2.5 millions d'années pour
former un corps de 1000km.