 Datation de la météorite «Allende»
Datation de la météorite «Allende»
Difficulté : ☆☆☆
La météorite dite « Allende », tombée en 1969 au Mexique, est probablement la météorite la plus étudiée de toute l’histoire. Elle est le représentant archétypal des chondrites carbonées, qui sont parmi les corps les plus primitifs du système solaire (cf. lien). Elle a de ce fait fortement contribué à faire connaître l’âge de notre système solaire à une très grande précision.
La méthode utilisée pour cette datation se base sur la désintégration U-Pb et sur la mesure des abondances relatives des différents isotopes du plomb.
Question 1)
La Figure présente les différentes mesures isotopiques effectuées en différents endroits de la météorite. En vous basant sur ce graphe, essayez d’estimer l’âge « d’Allende » en utilisant les formules présentées au chapitre «Comprendre ».
Attention: Les fractions isotopiques reportées sur le graphe ne sont pas forcément celles de la formule présentée dans le cours.
 Vidage de la zone d'alimentation des embryons
Vidage de la zone d'alimentation des embryons
Les phases d’accrétion boule-de-neige puis oligarchique produisent in fine un seul corps dominant (un « embryon ») à chaque distance radiale de l’étoile centrale (cf. cours « Accretion boule de neige », « Oligarchique » et « épuisement des ressources »). Un tel corps grossit en accrétant des petits planétésimaux et débris contenus dans sa « zone d’alimentation », c’est à dire un anneau radial à l’intérieur duquel tout corps aura une orbite croisant celle du corps dominant en raison de la focalisation gravitationnelle vers celui-ci (cf. lien). Pour un corps massif, la largeur de cette zone d’alimentation est environ égale à 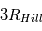 de chaque côté de l'orbite de la planète, où
de chaque côté de l'orbite de la planète, où 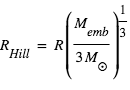 est le rayon de Hill correspondant à la « sphère d’influence » gravitationnelle du corps.
est le rayon de Hill correspondant à la « sphère d’influence » gravitationnelle du corps.
Question 1)
A) Montrer que la croissance par accrétion sur l’embryon va forcément finir par s’arrêter, car l’élargissement de la zone d’alimentation est plus lent que la croissance de l’embryon.
B) Estimer, pour une MMSN à 1UA du soleil, quelle est approximativement la masse atteinte par un embryon au moment où sa zone d’alimentation est vidée.
Ceci revient, en pratique, à comparer, pour une masse 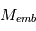 donnée, la masse totale disponible dans la zone d’alimentation à la masse de l’embryon lui même.
donnée, la masse totale disponible dans la zone d’alimentation à la masse de l’embryon lui même.
 Datation de la météorite «Allende»
Datation de la météorite «Allende»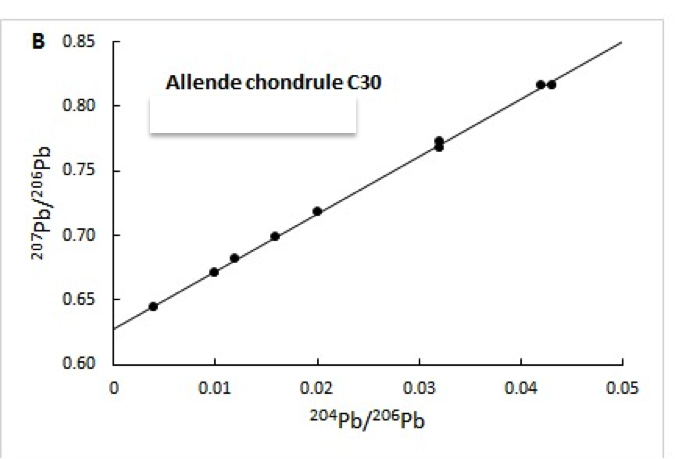
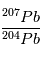 et
et 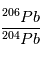 . Si tout se passe bien, on obtiendra alors une valeur pour le rapport
. Si tout se passe bien, on obtiendra alors une valeur pour le rapport 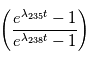 . Il n'y a hélas pas de solution analytique à cette équation. Pour trouver la valeur de t, on pourra s'aider d'un solveur numérique, comme par exemple
. Il n'y a hélas pas de solution analytique à cette équation. Pour trouver la valeur de t, on pourra s'aider d'un solveur numérique, comme par exemple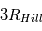 de chaque côté de l'orbite de la planète, où
de chaque côté de l'orbite de la planète, où 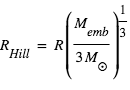 est le rayon de Hill correspondant à la « sphère d’influence » gravitationnelle du corps.
est le rayon de Hill correspondant à la « sphère d’influence » gravitationnelle du corps.
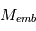 donnée, la masse totale disponible dans la zone d’alimentation à la masse de l’embryon lui même.
donnée, la masse totale disponible dans la zone d’alimentation à la masse de l’embryon lui même.