
Datation absolue |
La désintégration de 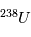 en
en 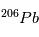 a un temps de ½ vie de 4.47 109 ans, idéal pour mesurer l’âge des plus anciens corps du système solaire. Mais
a un temps de ½ vie de 4.47 109 ans, idéal pour mesurer l’âge des plus anciens corps du système solaire. Mais 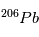 n’est pas l’isotope naturel du
n’est pas l’isotope naturel du 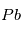 , qui est
, qui est 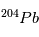 . On obtient alors la relation suivante, liant les abondances de
. On obtient alors la relation suivante, liant les abondances de 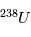 ,
, 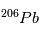 et
et 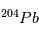 :
:
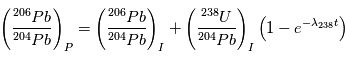
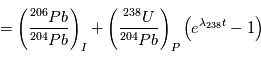
où les indices 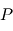 et
et 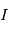 se réfèrent aux abondances actuelles et initiales, respectivement. Le moment "initial" correspond à l'instant où l'objet en question s'est solidifié pour la dernière fois. En effet, dès que le corps fond ou se sublime en gaz, les proportions des 2 isotopes
se réfèrent aux abondances actuelles et initiales, respectivement. Le moment "initial" correspond à l'instant où l'objet en question s'est solidifié pour la dernière fois. En effet, dès que le corps fond ou se sublime en gaz, les proportions des 2 isotopes 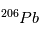 et
et 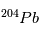 s'équilibrent rapidement à leur proportion "naturelle" et toute information sur la désintégration de
s'équilibrent rapidement à leur proportion "naturelle" et toute information sur la désintégration de 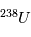 est perdue (voir page précédente ). A cet instant initial le rapport
est perdue (voir page précédente ). A cet instant initial le rapport 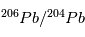 est donc égal à la valeur d'équilibre. En revanche, une fois le corps solidifié, un excès de l'isotope
est donc égal à la valeur d'équilibre. En revanche, une fois le corps solidifié, un excès de l'isotope 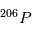 va petit à petit se créer à mesure que
va petit à petit se créer à mesure que 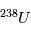 se désintègre. La variable inconnue est ici la quantité initiale absolue de
se désintègre. La variable inconnue est ici la quantité initiale absolue de 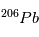 (ou de
(ou de 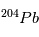 ), que l'on ne connaît pas a priori. Heureusement, il existe un deuxième type de désintégration d’U en Pb, la réaction
), que l'on ne connaît pas a priori. Heureusement, il existe un deuxième type de désintégration d’U en Pb, la réaction 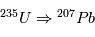 , dont le temps de vie est de 704 106 ans, et qui va nous permettre de contraindre les abondances initiales. Les équations sont alors:
, dont le temps de vie est de 704 106 ans, et qui va nous permettre de contraindre les abondances initiales. Les équations sont alors:
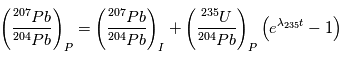
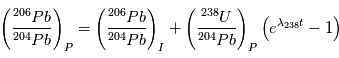
Et donc:
![F = \left [\frac{\left (\frac{{}^{207}Pb}{{}^{204}Pb} \right )_P -\left (\frac{{}^{207}Pb}{{}^{204}Pb} \right )_I }{ \left (\frac{{}^{206}Pb}{{}^{204}Pb} \right )_P - \left (\frac{{}^{206}Pb}{{}^{204}Pb} \right )_I} \right ]=\left ( \frac{1}{137.88} \right )\left ( \frac{e^{\lambda {}_{235}t} -1}{e^{\lambda {}_{238}t} -1} \right )](../pages_planetologie-formation/equations_datation-radio-isotopique/equation41.png)
où 137.88 est la valeur présente de 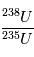 , qui est une constante globale du système solaire actuel, et
, qui est une constante globale du système solaire actuel, et 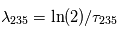 ,
, 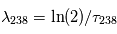 . Cette relation est directement exploitable pour toute météorite non-homogène initialement, mais dont tous les composants se sont formés à la même époque. En effet, dans ce cas, les rapports initiaux
. Cette relation est directement exploitable pour toute météorite non-homogène initialement, mais dont tous les composants se sont formés à la même époque. En effet, dans ce cas, les rapports initiaux 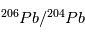 et
et 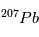 /
/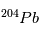 sont les mêmes partout dans la météorite et sont égaux à leurs valeurs d'équilibre (indiquées par a0 et b0 sur la figure). Par conséquent, dans un graphe
sont les mêmes partout dans la météorite et sont égaux à leurs valeurs d'équilibre (indiquées par a0 et b0 sur la figure). Par conséquent, dans un graphe 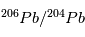 vs.
vs. 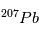 /
/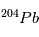 , toutes les mesures du rapport F doivent se situer une même droite, appelée isochrone, dont la pente va directement donner l’âge de la météorite (cf. Figure).
, toutes les mesures du rapport F doivent se situer une même droite, appelée isochrone, dont la pente va directement donner l’âge de la météorite (cf. Figure).