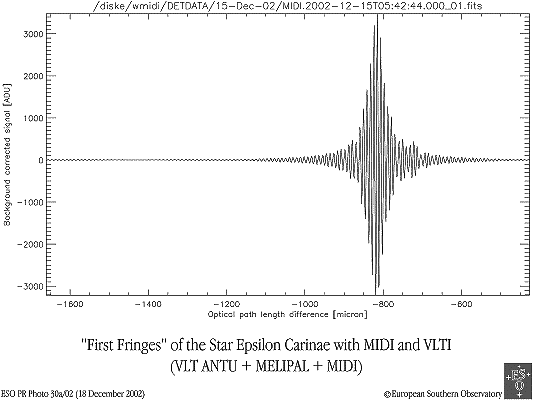
Enregistrement de franges d'interférence. La cohérence spatiale est limitée par la taille angulaire de la source.
Crédit :
ESO
Mesure de visibilité
Un interféromètre enregistre des franges d'interférence, pour en déterminer la visibilité. Celle-ci décroît rapidement dès que l'interférogramme s'écarte de la différence de marche correspondant au déphasage nul entre les 2 signaux.
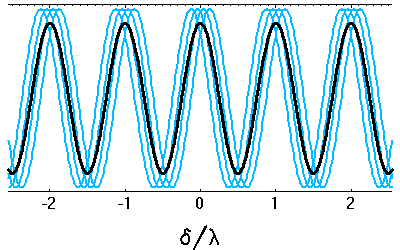
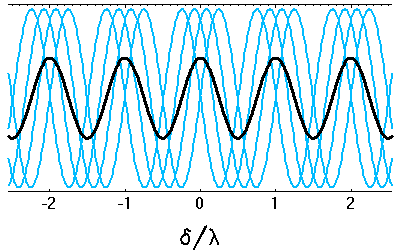
Cohérence spatiale : la superposition des différentes contributions déphasées amoindrit la visibilité des franges.
Crédit :
ASM
Source étendue
La cohérence spatiale entre 2 points d'un écran dépend de l'étendue angulaire de la source.

Tache de diffraction récupérée par optique adaptative (NACO/VLT) en bande K.
Crédit :
ESO
Source ponctuelle
L'image d'une source ponctuelle n'est pas un point : c'est la diffraction qui le veut... c'est un cas particulier de la notion de cohérence spatiale.
 Objectifs
Objectifs
Le cas d'une source rigoureusement ponctuelle et monochromatique est
souvent évoqué pour aborder l'optique (géométrique ou physique). Une source réelle en astrophysique peut être
approximativement ponctuelle, du fait d'un très grand éloignement, mais ce
n'est pas toujours le cas.
La cohérence spatiale rend compte de l'étendue angulaire de la source.
Une analyse détaillée des phénomènes peut se traiter par une formalisme
mathématique et s'appuie sur le théorème Zernike Van-Cittert.
Cohérence spatiale
Les sources astrophysiques ne sont pas naturellement cohérentes. Leur
étendue angulaire va conduire à dégrader la cohérence du rayonnement : l'onde collectée mélange diverses directions incidentes, présentant différentes phases, dont le mélange dégrade la cohérence.
Pour modéliser ce phénomène, on s'intéresse à la cohérence du champ sur un écran illuminé par une source à grande distance ; cet écran illustre le rôle que joue un plan d'onde intermédiaire ou bien une pupille.
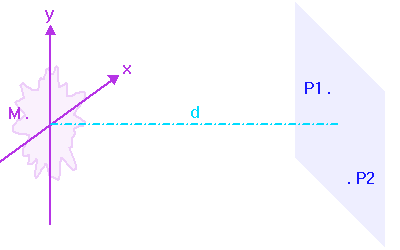
Cohérence du champ vu depuis 2 points P1 et P2 d'un écran E.
Crédit :
ASM
Cohérence du rayonnement d'une source circulaire.
Crédit :
ASM
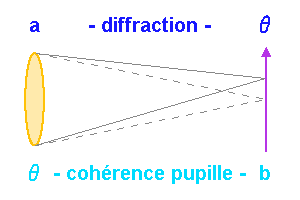
Ce schéma montre l'analogie entre le calcul de la tache de diffraction par une pupille circulaire de rayon
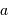
, et la cohérence du champ d'une source de diamètre
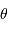
entre 2 points d'un écran séparés de
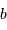
.
Crédit :
ASM
Rappel sur la diffraction de Fraunhofer
Le résultat précédent ressemble furieusement à celui de la diffraction. Est-ce un hasard ?
La tache d'Airy résultant de la diffraction par une pupille circulaire rend compte de la contribution de toutes les sources secondaires à considérer sur la pupille. Plus la pupille est grande, plus les déphasages s'accumulent dès lors que l'on s'éloigne de la position centrale de l'image géométrique. Il s'ensuit que la tache de diffraction est d'autant plus piquée que la pupille est grande.
En terme de cohérence, plus une pupille est grande, plus le degré de cohérence entre 2 points de cette pupille diminue.
Une autre manière de reformuler ceci dérive de l'analyse de Fourier :
plus on possède d'information sur un signal, moins ce signal est localisé.
Le principe d'incertitude de Heisenberg ne dit pas autre chose : la détermination précise d'une grandeur nécessite que sa grandeur conjuguée soit étendue, la moins localisée possible.
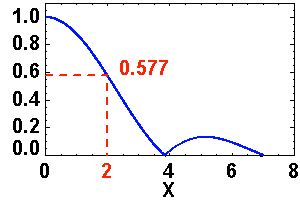
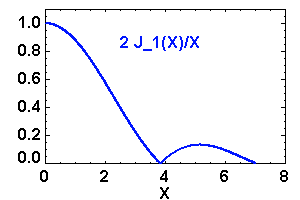
Etendue de cohérence : la valeur à mi-hauteur est obtenue pour
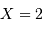
.
Crédit :
ASM
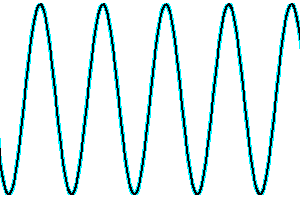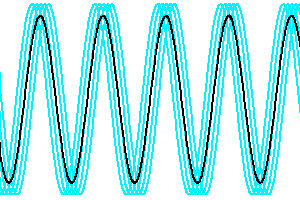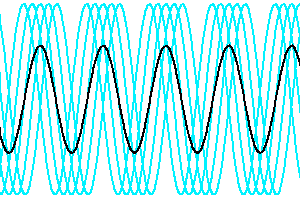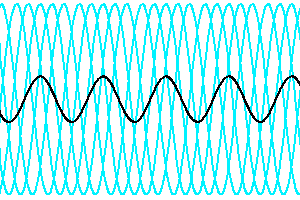
Evolution de la cohérence spatiale en fonction des déphasage des faisceaux issus de différents points de la source.
Crédit :
ASM
Visibilité fonction du degré de cohérence de la pupille
La visibilité du signal d'interférence dépend des déphasages entre les faisceaux issus des différents points de la source. Plus ces déphasages augmentent, moins le signal est cohérent.





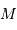 de la source par le rayon vecteur
de la source par le rayon vecteur 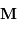 de coordonnées
de coordonnées 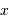 et
et 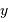 . On compare la cohérence entre 2 points
. On compare la cohérence entre 2 points 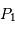 et
et 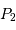 de l'écran.
Pour une source à grande distance (
de l'écran.
Pour une source à grande distance (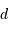 très grand par rapport aux autres dimensions), on définit le degré de cohérence comme une fonction du profil de brillance
très grand par rapport aux autres dimensions), on définit le degré de cohérence comme une fonction du profil de brillance 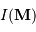 :
:
![\gamma_{1,2} \ = \ \gamma (\mathbf{P_1P_2}) \ = \ { \displaystyle{\int _{\mathrm{source}} I( \mathbf{M})\ \exp \left[ -2i\pi\ { \mathbf{M} \over d}. {\mathbf{P_1P_2} \over \lambda} \right] \ {\mathrm{d}}^2 \mathbf{M}} \over \displaystyle{\int _{\mathrm{source}} I( \mathbf{M}) \ {\mathrm{d}}^2 \mathbf{M}} }](../pages_rayon/equations_coherence-spatiale/equation9.png)

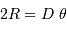 ,
de brillance uniforme, observée à distance
,
de brillance uniforme, observée à distance 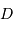 . La brillance peut être représentée par une fonction porte
. La brillance peut être représentée par une fonction porte 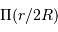 . On traite alors ce cas particulier en s'appuyant sur sa géométrie cylindrique, et
l'on réécrit la cohérence entre le centre
. On traite alors ce cas particulier en s'appuyant sur sa géométrie cylindrique, et
l'on réécrit la cohérence entre le centre 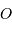 de l'écran (centre repéré sur la normale à l'écran vers la source) et un point
de l'écran (centre repéré sur la normale à l'écran vers la source) et un point 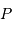 tel
tel 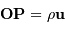 :
:
![\begin{eqnarray*} \gamma_{1,2} \ =& { \displaystyle{\int _{\mathrm{source}} \ \Pi{\left({D \mathbf{u}\over 2R } \right)}\exp\left[ -2i\pi\ \mathbf{u} . {\mathbf{\rho} \over \lambda}\right] \ {\mathrm{d}} \mathbf{u}} \over \displaystyle{\int _{\mathrm{source}} \Pi{\left({D \mathbf{u}\over 2R } \right)}\ {\mathrm{d}} \mathbf{u}} }\\ \propto & \displaystyle{\int_0^\theta \ \exp\left[ -2i\pi\ \mathbf{u} . {\mathbf{\rho} \over \lambda}\right] \ {\mathrm{d}} \mathbf{u}} \ = \ \displaystyle{ 2 J_1 \left( 2\pi\theta \displaystyle{\rho\over \lambda}\right) \over 2\pi\theta \displaystyle{\rho\over \lambda}}\\ = & \displaystyle{ 2 J_1 (X) \over X} \ \ \mathrm{avec} \ \ X\ =\ 2\pi\theta \displaystyle{\rho\over \lambda} \end{eqnarray*}](../pages_rayon/equations_coherence-spatiale/equation16.png)
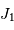 .
.

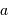 , et la cohérence du champ d'une source de diamètre
, et la cohérence du champ d'une source de diamètre 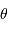 entre 2 points d'un écran séparés de
entre 2 points d'un écran séparés de 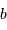 .
.

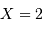 .
.
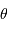 est vue depuis l'écran sous un angle solide
est vue depuis l'écran sous un angle solide 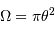 . Une surface
. Une surface 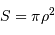 de l'écran correspond à une
de l'écran correspond à une 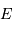 telle que :
telle que :
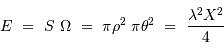
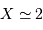 : on choisit cette valeur pour définir le rayon de l'étendue de cohérence.
: on choisit cette valeur pour définir le rayon de l'étendue de cohérence.
 .
.
