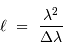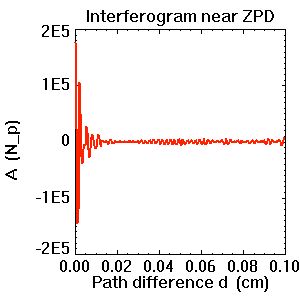
Portion de la partie modulée d'un interférogramme. Le contraste des franges s'écroule dès lors que l'on s'éloigne de la différence de marche nulle.
Crédit :
ASM
Interférogramme
Un interféromètre de Michelson permet de tracer l'interférogramme d'une source, càd la figure d'interférence obtenue après déphasage de l'une des 2 voies de l'interféromètre d'une différence de marche 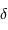 .
L'interférogramme du
spectre d'une source réelle, délimitée par un intervalle spectral
fini, illustre le phénomène de cohérence temporelle : le signal
d'interférence chute dès lors que la différence de marche devient
grande.
.
L'interférogramme du
spectre d'une source réelle, délimitée par un intervalle spectral
fini, illustre le phénomène de cohérence temporelle : le signal
d'interférence chute dès lors que la différence de marche devient
grande.
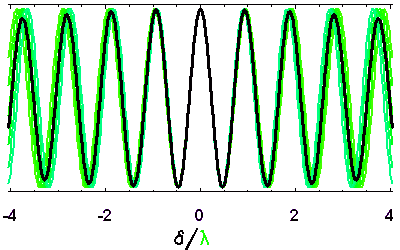
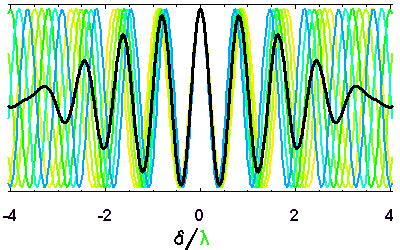
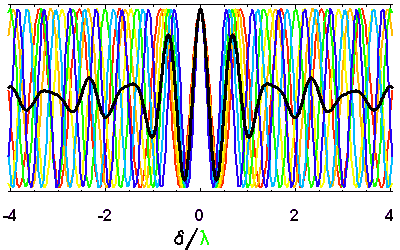
Evolution de la longueur de cohérence temporelle en fonction de la largeur spectrale. Plus l'intervalle spectral accepté est large, plus vite le signal est moyenné dès lors que la différence de marche s'éloigne de la valeur nulle.
Crédit :
ASM
Cohérence temporelle et intervalle spectral
La cohérence temporelle décroît d'autant plus rapidement que le spectre de la source présente une gamme de longueurs d'onde importante.
 Objectifs
Objectifs
Le cas d'une source rigoureusement ponctuelle et monochromatique est
souvent évoqué pour aborder l'optique géométrique et physique. Une source ne sera jamais totalement monochromatique,
même si son spectre présente des raies d'émission très étroites, ou si
par dispersion ou filtrage on sélectionne un très fin domaine
spectral. La cohérence temporelle d'une onde rend compte de sa chromaticité.
Une approche rigoureuse passe par le théorème de Wiener-Khintchine.
 Prérequis
Prérequis
Interféromètre de Michelson
Cohérence temporelle
Tout phénomène d'interférence avec une source monochromatique conduit à une modulation de l'amplitude résultante fonction de la longueur d'onde du rayonnement.
Pour une source polychromatique, mélanger les couleurs revient donc à mélanger des périodes différentes : la cohérence temporelle du signal est prise en défaut.
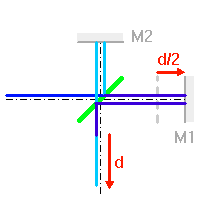
Interféromètre de Michelson : les 2 faisceaux, après recombinaison, sont décalés d'une différence de marche
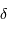
.
Crédit :
ASM
Exemple : interférométrie par transformée de Fourier
(Ne pas hésiter à aller voir les pages dédiées au spectromètre par TF).
L'exemple d'un interféromètre par transformée de Fourier (réglé en anneau) présente la problématique :
la visibilité des franges décroît d'autant plus rapidement que le
domaine spectral accepté est vaste.
Pour une raie monochromatique, l'interférogramme se développe, en fonction de la différence de marche, comme :
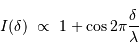
Pour une raie réelle, présentant une largeur non infiniment fine, il faut tenir compte de la contribution des différentes composantes spectrales.
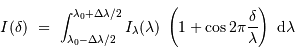
L'intégration, fonction du profil spectral 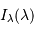 de la raie, conduit à :
de la raie, conduit à :
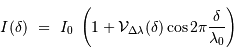
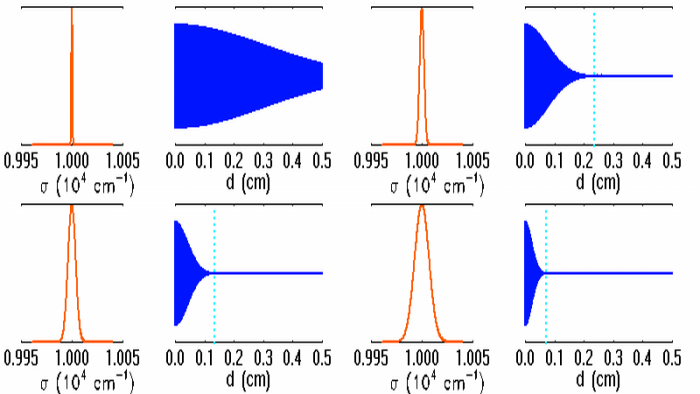
Profils de raie et visibilités associées.
Crédit :
ASM
L'expression de la fonction de visibilité des franges 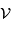 dépend de l'intégration du profil spectral
dépend de l'intégration du profil spectral 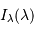 , et n'est pas nécessairement simple. La visibilité :
, et n'est pas nécessairement simple. La visibilité :
- a une extension inversement proportionnelle à
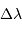 ; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.
; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles. - décroît avec la différence de marche
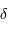 .
.
Un exemple de démonstration, dans un cas simplifié, est donné en exercice.
Définition de la cohérence temporelle
Dans le cas général, le degré de cohérence d'une source polychromatique, complexe, s'écrit :
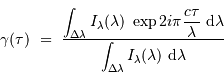
La démonstration résulte du théorème de Wiener-Khintchine.
La longueur de cohérence 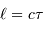 , qui mesure l'étendue du degré de cohérence, vérifie approximativement :
, qui mesure l'étendue du degré de cohérence, vérifie approximativement :
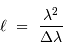
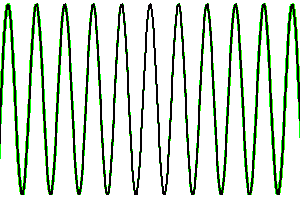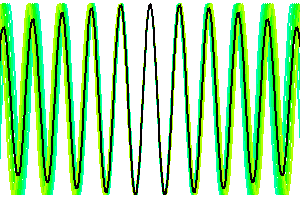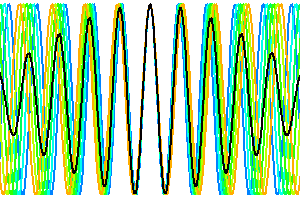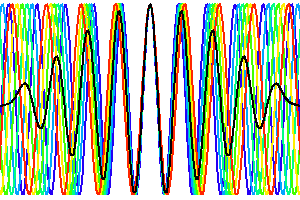
Evolution de la longueur de cohérence temporelle en fonction de la largeur spectrale.
Crédit :
ASM
Visibilité fonction de l'intervalle spectral
La visibilité des franges d'interférences dépend de la largeur de l'intervalle spectral considéré. La superposition de franges de couleurs différentes, donc de périodes différentes, conduit à un signal d'interférence en moyenne nulle.

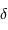 .
L'interférogramme du
spectre d'une source réelle, délimitée par un intervalle spectral
fini, illustre le phénomène de cohérence temporelle : le signal
d'interférence chute dès lors que la différence de marche devient
grande.
.
L'interférogramme du
spectre d'une source réelle, délimitée par un intervalle spectral
fini, illustre le phénomène de cohérence temporelle : le signal
d'interférence chute dès lors que la différence de marche devient
grande.




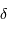 .
.
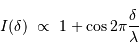
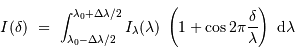
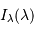 de la raie, conduit à :
de la raie, conduit à :
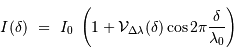

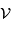 dépend de l'intégration du profil spectral
dépend de l'intégration du profil spectral 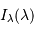 , et n'est pas nécessairement simple. La visibilité :
, et n'est pas nécessairement simple. La visibilité :
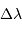 ; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.
; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.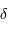 .
.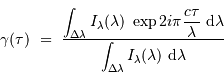
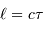 , qui mesure l'étendue du degré de cohérence, vérifie approximativement :
, qui mesure l'étendue du degré de cohérence, vérifie approximativement :