 Introduction
Introduction
Compte tenu des conditions de température et d'irradiation de l'atmosphère solaire, les mesures in situ sont très difficiles. Les sondes se sont approchées à 0.3 Unités Astronomiques du Soleil. Des projets sont en cours d'élaboration pour pénétrer à une distance de 3 rayons solaires dans la couronne. De même, si le vent solaire peut être étudié in situ autour de la Terre et jusque dans les régions des premières planètes géantes, les mesures aux confins de l'héliosphère sont rares et difficiles (seules les sondes VOYAGER, lancées en 1977, ont atteint ces limites en 2004 et 2007).
Pour comprendre les processus physiques se déroulant à l'intérieur du Soleil, dans son atmosphère et aux confins de l'héliosphère, nous n'avons pas d'autre choix que d'étudier le rayonnement électromagnétique qui nous parvient, des rayons γ au rayonnement radio. Les processus d'émission des ondes renseignent sur les conditions physiques au moment de l'émission et dans les régions traversées par ce rayonnement.
Emissions thermiques et non-thermiques
Différents types mécanismes d'émission de rayonnement électromagnétique coexistent.
L'agitation des particules constituant un gaz produit un rayonnement continu, dans tout le spectre électromagnétique. C'est le rayonnement thermique. A ce spectre continu se superposent des absorptions (ou émissions) très localisées dans le spectre provenant de processus non-thermiques.
Nous allons voir les principaux types d'émission et les propriétés qu'elles permettent de déduire.
La "lumière" peut être décrite sous la forme d'une onde ou sous la forme d'une particule (le photon). Ces deux notions se sont imposées pour décrire correctement l'interaction de la "lumière" avec des structures solides ou des atomes. Ce que nous appelons communément la "lumière" se réfère en fait à la gamme visible de l'émission d'un Soleil. Mais le Soleil, comme la plupart des étoiles, émet dans une gamme beaucoup plus étendue de longueur d'onde.
Longueur d'onde et énergie
Le rayonnement électromagnétique est constitué par un champ électrique et un champ magnétique (dont le vecteur est perpendiculaire au champ électrique) qui oscillent. Une onde est définie par la fréquence de cette oscillation et l'amplitude du champ électrique (l'amplitude du champ magnétique peut être négligée pour ce qui nous intéresse).
Longueur d'onde λ et fréquence ν sont reliées par l'équation : 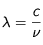
où c est la vitesse de la lumière. Donc, plus une longueur d'onde est grande plus la fréquence est petite.
L'énergie d'une onde est donnée par : E = hν
où h est la constante de Planck (h=6,6 10-34 J.s). Donc, plus la fréquence est petite (grande longueur d'onde) plus l'énergie de l'onde est petite.
La distribution de l'énergie émise en fonction de la longueur d'onde (ou de la fréquence) s'appelle un spectre.
Les domaines spectraux
Le spectre électromagnétique s'étend de façon continue des rayons gamma (très courte fréquence, très grande énergie) au domaine des ondes radio de très grandes longueurs d'onde. Le tableau suivant donne le nom des différents domaines et leurs limites en longueur d'onde.
| Nom du domaine spectral |
Longueur d'onde |
| Gamma - X (dur) |
<0,1 nm |
| X (mous) |
0,1 - 10 nm |
| Extrême UltraViolet (EUV) |
10 - 120 nm |
| UltraViolet (UV) |
120 - 400 nm |
| Visible |
400 - 800 nm |
| Infra-Rouge (IR) |
800nm - 1 mm |
| Radio |
>1 mm |
Noms et limites (en longueur d'onde) des différents domaines spectraux. L'abbréviation classique des différents domaines est aussi indiquée avec le nom.
L'agitation thermique des particules constituant un corps produit un rayonnement continu, dans tout le spectre électromagnétique. Ce rayonnement thermique est décrit par la loi du corps noir (absorbant parfait).
Le Soleil, comme la plupart des étoiles, rayonne comme un corps noir. La loi fondamentale, la loi de Planck, donne l'intensité (autrement appelée luminance) en fonction de la longueur d'onde :
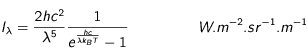
avec :
h la constante de Planck (h=6,6 10-34 J.s), c la vitesse de la lumière (c=3 108 m.s-1) et 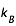 la constante de Boltzman (
la constante de Boltzman (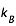 =1,38 10-23 J.K-1)
=1,38 10-23 J.K-1)
L'intensité décrit donc la puissance rayonnée par unité de surface, d'angle solide et de longueur d'onde. La figure ci-contre montre la courbe d'intensité pour des étoiles de température différente en fonction de la longueur d'onde. Deux points sautent aux yeux :
- Le maximum de l'intensité est d'autant plus élevé que la température de surface de l'étoile est grande
- La longueur d'onde du pic de maximum d'intensité se décale vers les petites longueurs d'onde (vers le bleu) avec l'augmentation de la température de surface de l'étoile
Ces deux remarques sont exprimées par deux lois lois simplifiées déduites de la loi de Planck.
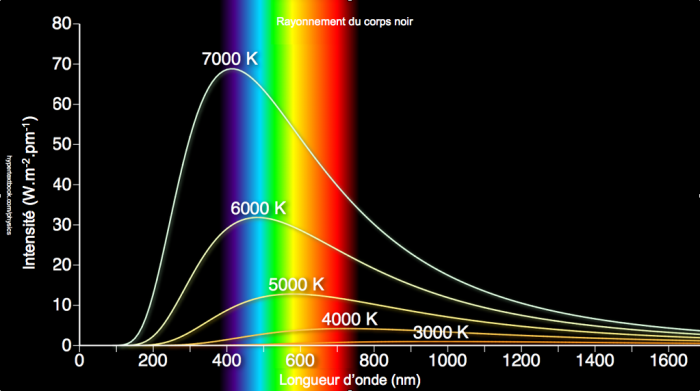
Intensité du spectre électromagnétique en fonction de la longueur d'onde pour des étoiles de température de surface différente. Ces courbes sont l'illustration de la loi de Planck. Les domaines UV, X et gamma sont vers la gauche de la figure, l'infra-rouge et la radio vers la droite.
Crédit :
Adapté du graphe original de Glenn Elert - http://hypertextbook.com/physics/
Loi de Wien
La loi de Wien relie la longueur d'onde maximale 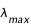 à la température de surfaceT :
à la température de surfaceT :
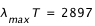 μm.K
μm.K
Nous retrouvons bien que plus une étoile est chaude plus la longueur d'onde du maximum d'intensité est petite (vers le bleu).
loi de Stephan
La loi de Stephan donne l’émission totale (en tenant compte de toutes les longueurs d'onde) du corps par unité de surface :

Avec σ = 5,6698 x 10-8 W.m-2.K-4
Les basses fréquences
Enfin, considérons le cas où le terme dans l'exponentielle de la loi de Planck est petit :
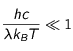
La loi de Planck se simplifie alors pour donner la loi de Rayleigh-Jeans :
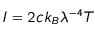
Dans le cas des basses fréquences (grandes longueurs d'onde), l'intensité est directement proportionnelle à la température.
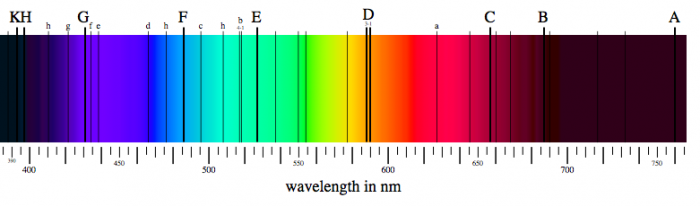
Le rayonnement thermique donne un spectre continu. Cependant, si nous regardons attentivement le spectre solaire, nous nous apercevons qu'il est parsemé de stries noires. Elles sont appelées "raies d'absorption" car elles correspondent à l'absorbtion du rayonnement (le fond continu) par des atomes présents (principalement) dans l'atmosphère du Soleil.

Spectre solaire dans le domaine visible. Sur un fond continu correspondant au rayonnement thermique se superposent des raies noires, appelées raies d'absorption.
Crédit :
Observatoire de Paris
Raies d'absorption
L'état énergétique d'un atome, d'un ion ou d'une molécule n'est pas continu mais quantifié. Un atome passe d'un niveau d'énergie à un autre par palier (par la suite nous ne parlerons que d'atome pour ne pas alourdir le texte mais ce qui est décrit s'applique également aux ions et aux molécules).
Un atome absorbe (ou émet) de l'énergie correspondant à chaque saut de palier. Ainsi, un photon qui possède une énergie exactement égale à un saut énergétique d'un atome donné sera absorbé.
Chaque atome possède une "carte énergétique" propre : les sauts autorisés pour le fer par exemple ne sont pas ceux du carbone ou de l'hydrogène. Ainsi, la position de ces raies d'absorption permettent de connaître les éléments présents dans l'atmosphère solaire. La "carte énergétique" d'un atome est connue par les physiciens atomistes.
L'hélium a ainsi été découvert sur le Soleil avant d'être trouvé sur Terre, d'où son nom !
Raies d'émission
Les atomes ayant absorbé de l'énergie sont dits excités. Ils ne resteront pas dans cet état pour une longue durée. Ils vont se désexciter en retombant directement ou par paliers successifs dans un état énergétique plus stable.
Ce faisant, ils vont émettre des photons (paquets d'onde électromagnétique) correspondants à ce(s) saut(s) énergétique(s). Autrement dit, un atome peut émettre un photon à la même énergie qu'il peut en absorber. La longueur d'onde d'émission (d'absorption) est directement liée au saut énergétique franchi :
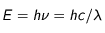
avec h la constante de Planck, c la vitesse de la lumière, 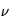 la fréquence et
la fréquence et 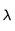 la longueur d'onde. Ainsi, plus la longueur d'onde est grande (fréquence petite) plus l'énergie du photon est petite.
la longueur d'onde. Ainsi, plus la longueur d'onde est grande (fréquence petite) plus l'énergie du photon est petite.
Nous avons vu le processus d'émission et d'absorption de la lumière par un atome en l'appliquant dans le domaine visible du spectre solaire. Mais le phénomène conduit également à des l'absorption et de l'émission dans l'infrarouge ou l'ultraviolet.
Profils spectraux
La figure ci-contre montre un exemple de profils de raie : il s'agit simplement d'une coupe horizontale dans le spectre montré précédemment. Les atomes ou molécules ayant produit ces raies d'absorption sont indiqués. Des éléments lourds tels que du magnésium (Mg), du fer (Fe) ou du carbone (C) sont présents. Ces atomes n'ont pas été produit par le Soleil. Ils proviennent du nuage protosolaire. Ce sont donc des résidus d'anciennes étoiles ayant explosées dans le passé.
Le phénomène d'absorption se produit tout au long du parcours des photons entre leur point d'émission et celui d'observation. En ce qui concerne le rayonnement solaire, une autre source d'absorption est aussi présente lors d'observation depuis le sol : l'atmosphère terrestre. C'est ainsi que l'on voit apparaître la signature de molécule d'eau sur le spectre solaire. Est-ce à dire qu'il y a de l'eau sur le Soleil ? Non, bien sûr. Pour bien s'en convaincre, il suffit de regarder comment ces raies disparaissent d'un moment à l'autre de la journée ou d'une journée à l'autre. L'absorption est en effet plus ou moins forte selon la densité de molécules absorbantes le long du trajet du rayonnement.
Comme on peut le constater sur la figure, la profondeur relative des raies varie énormément. Certaines raies produisent une absorption d'à peine 10% alors que les raies du Mg produisent une absorption de près de 90% du rayonnement. La forme, la profondeur, la largeur et la position de ces raies vont fournir des indicateurs pour déduire la température, la densité et la vitesse moyenne du milieu.
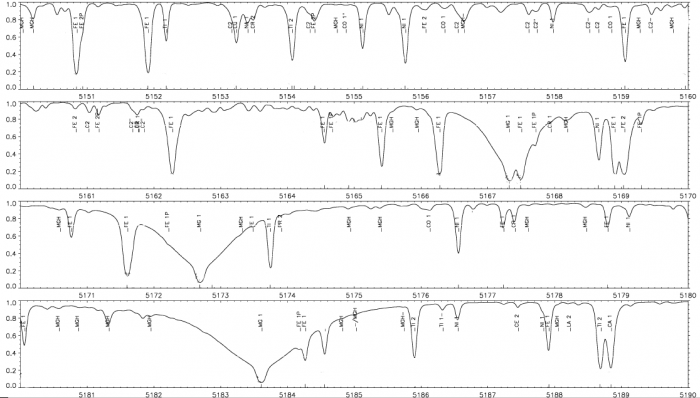
Profils spectraux de plusieurs raies dans la gamme 514.0-518.0 nm. Le nom des éléments ayant créé les raies d'absorption les plus importantes est indiqué.
Crédit :
Extrait du spectre solaire établit par Delbouille - Disponible sur BASS2000
Les raies ne sont pas toutes formées à la même altitude dans l'atmosphère du Soleil (voir un exemple ici). En observant des raies formées à différentes altitudes, on peut ainsi déduire une carte non seulement en deux dimensions (le plan d'observation) mais en trois dimensions du Soleil (en ajoutant la hauteur grâce à des observations simultanément dans plusieurs raies spectrales).
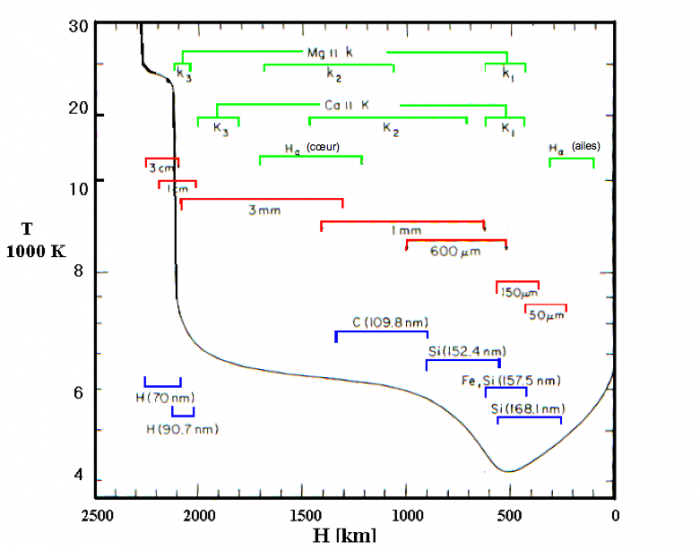
Altitude de formation de certaines raies. La courbe en noire représente la température en fonction de l'altitude (l'altitude H=0 est la base de la photosphère). Le nom des éléments donnant les raies est indiqué ainsi que la longueur d'onde correspondante.
Crédit :
Adapté des Modèles d'atmopshère solaire VAL
 En savoir plus
En savoir plus
Comment peut-on déduire température, densité, vitesse ?
Sans entrer dans le détail car c'est un domaine fort compliqué, surtout en physique solaire où les détails des profils spectraux sont si fins que beaucoup de processus physiques doivent être pris en compte. Nous allons juste en donner les grandes lignes.
Cette ligne de recherche s'appelle le transfert de rayonnement. Comme son nom l'indique, il s'agit de comprendre comment le rayonnement est transféré d'une couche à l'autre de l'atmosphère en prenant en compte tous les processus d'émission et d'absorption.
On considère un morceau de plasma illuminé par dessous. L'intensité du rayonnement incident sur cette tranche de plasma est prédéfinie par un modèle (par exemple la loi du corps noir). Ensuite, on établit un modèle d'atmosphère pour notre tranche de plasma. Elle a donc une composition (avec un plus ou moins grand nombre d'atomes selon la raie que l'on veut modéliser), une densité (pour chacun des atomes inclus), une température, une vitesse. Nous nous plaçons pour l'instant dans le cas ou nous pouvons négliger la présence d'un champ magnétique.
Le rayonnement incident d'intensité I va donc traverser cette tranche de Soleil fictif. Il subira un certain nombre d'absorption et d'émission. Quelle intensité 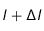 peut-on espérer à la sortie de notre tranche de plasma ? Quelle forme aura le profil de la raie qui nous intéresse ?
peut-on espérer à la sortie de notre tranche de plasma ? Quelle forme aura le profil de la raie qui nous intéresse ?
Tout revient à connaître précisément le taux d'émission et d'absorption dans notre tranche de plasma. C'est là que les soucis commencent ... Selon que le milieu laisse ou non passer tout ou partie des photons les équilibres à écrirent deviennent plus complexes. Des connaissances précises des transitions énergétiques autorisées pour chaque élément sont nécessaires. C'est là que les "physiciens atomistes" interviennent pour nous aider !!
Les équations sont rentrées en un programme qui va traiter l'avancement des photons au sein de chaque tranche de plasma dont l'accumulation représentera l'atmosphère totale. Le profil de raie résultant sera alors comparé aux observations. Si le modèle ne donne pas satisfaction, le modèle atmosphérique est changé jusqu'à obtenir un résultat ajustant les observations.
Ce processus itératif peut être optimisé par une connaissance précise de l'impact des différents paramètres (température, densité, etc.) sur les raies. Certaines raies sont en effet plus sensibles à la température alors que d'autres seront plus sensibles à la densité. Rapidement, la température va influencer la largeur d'une raie, la densité la profondeur de la raie et la vitesse la position de la raie.
Introduction
Tous les photons ne sont pas dus à des transitions des électrons d'un atome. Un très grand nombre d'entre eux sont émis suite à l'accélération d'une particule chargée. On distingue alors plusieurs sortes de rayonnement en fonction du type d'accélération subit par la particule.
En particulier, le Soleil, le milieu interplanétaire et les planètes produisent de larges émissions dans le domaine radio. Nous allons maintenant en voir quelques exemples.
Sursauts solaires de type II et III
Lors d'éruptions solaires, des particules sont accélérées à de très fortes énergies. Ces particules se propagent le long des lignes de champ magnétique interplanétaire, formant parfois des faisceaux de particules. En se propageant, ces particules vont provoquer des émissions dans le domaine radio. Nous allons voir les processus de base de ces émissions (le détail est en dehors des limites de ce cours : c'est encore un sujet d'investigation fortement débattu !)
On distingue deux types d'émissions radio : les émissions de type II et de type III. Un exemple de ces émissions est présenté sur la figure figure ci-contre. Ce rayonnement électromagnétique est caractérisé par une dérive en fréquence de l'émission en fonction du temps. Du point de vue observationnel, la différence principale entre ces deux types d'émission réside dans la pente de la dérive de l'émission avec le temps : les émissions de type III dérivent beaucoup plus vite que les émissions de type II.
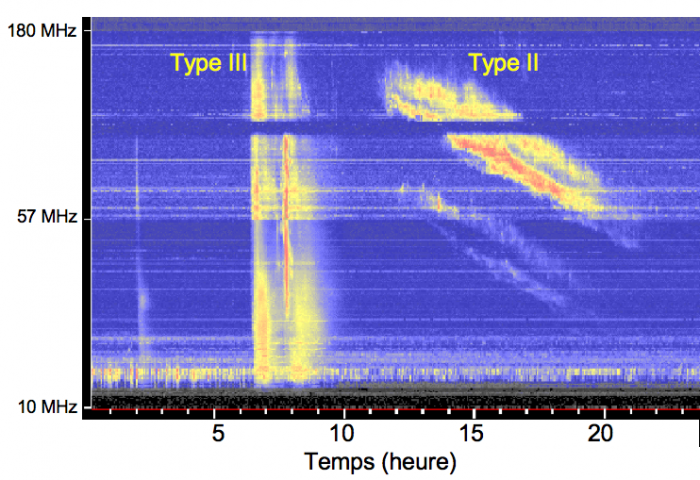
Exemple d'émission radio de type II et III : le temps est en abscisse, la fréquence est en ordonnée. Ce type de diagramme est appelé spectre dynamique car il donne la répartition de l'énergie radio (code de couleur : bleu très faible intensité, rouge : très forte intensité) en fonction de la fréquence (ici de 10 à 180 MHz) et du temps (ici de 0 à 24h).
Crédit :
IPS Radio and Space Services, Australia
Les faisceaux en se déplaçant dans le milieu interplanétaire produisent ce que l'on appelle des "ondes de Langmuir" à une fréquence proche d'une fréquence particulière appelée "fréquence plasma" qui s'écrit :
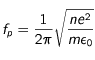
avec 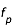 la fréquence plasma (en Hz),
la fréquence plasma (en Hz), 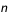 est la densité d'électrons,
est la densité d'électrons, 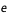 la charge élémentaire (1,6 x 10-19 c),
la charge élémentaire (1,6 x 10-19 c), 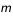 la masse de l'électron (9 x 10-31kg),
la masse de l'électron (9 x 10-31kg), 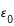 la constante diélectrique (8,8 x 10-12 F. m-1).
la constante diélectrique (8,8 x 10-12 F. m-1).
Pour concrétiser le sujet, supposons que nous soyions dans le vent solaire. Une densité typique est 10 particules.cm-3. La fréquence plasma vaut alors 28 kHz : nous sommes dans la gamme des ondes radio.
Ces ondes sont électrostatiques : elles ne se propagent pas. Seules des mesures dans la source de ces ondes permettent de les mesurer, et donc de déterminer la densité n du milieu. Toutefois, par certains processus, ces ondes sont transformées en ondes électromagnétiques qui, elles, vont se propager et qui sont à une fréquence proche de cette fréquence plasma.
Que nous apprennent ces ondes ?
Comme le faisceau se déplace dans un milieu dont la densité décroit quand la distance au Soleil augmente, la fréquence diminue avec le temps. C'est ce qui explique la dérive en fréquence des émissions avec le temps.
On utilise ces pentes de dérive pour déterminer la vitesse des faisceaux de particules. En effet, on peut montrer que la pente peut s'écrire :
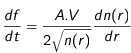
où df/dt représente la variation de la fréquence en fonction du temps (la pente dans le diagramme précédent), 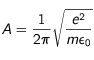 , V la vitesse du faisceau d'électrons, n(r) un modèle de densité électronique en fonction de la distance au Soleil et dn(r)/dr la variation de cette densité en fonction de la distance au Soleil. Donc, si l'on se donne un modèle de densité électronique dans le milieu interplanétaire, on peut déduire V à partir de la mesure de pente df/dt.
, V la vitesse du faisceau d'électrons, n(r) un modèle de densité électronique en fonction de la distance au Soleil et dn(r)/dr la variation de cette densité en fonction de la distance au Soleil. Donc, si l'on se donne un modèle de densité électronique dans le milieu interplanétaire, on peut déduire V à partir de la mesure de pente df/dt.
 En savoir plus
En savoir plus
Ce mécanisme d'émission de rayonnement résulte du comportement collectif des particules - des électrons - accélérées. En effet, si un plasma subit une perturbation, ses électrons vont spontanément et collectivement se mettre à osciller à la fréquence particulière appelée fréquence plasma. Elle donne l'échelle de temps caractéristique de la réponse collective des électrons à la perturbation (les protons, beaucoup trop massifs, peuvent être considérés comme immobiles). C'est une des caractéristiques fondamentales d'un plasma.
Cette fréquence est donnée par :
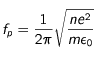
avec 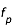 la fréquence plasma (en Hz),
la fréquence plasma (en Hz), 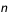 est la densité d'électrons,
est la densité d'électrons, 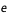 la charge élémentaire (1,6 x 10-19 c),
la charge élémentaire (1,6 x 10-19 c), 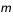 la masse de l'électron (9 x 10-31kg),
la masse de l'électron (9 x 10-31kg), 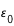 la constante diélectrique (8,8 x 10-12 F. m-1). Si on peut mesurer la fréquence plasma, on peut déterminer la densité du milieu. Les ondes à cette fréquence sont électrostatiques : elles sont constituées par un champ électrique qui oscille, sans champ magnétique - contrairement à des ondes électromagnétiques - et ne se propagent pas. Elles sont convectées par le milieu si celui-ci se déplace ; c'est donc par le biais de mesures in-situ que l'on peut les mesurer.
la constante diélectrique (8,8 x 10-12 F. m-1). Si on peut mesurer la fréquence plasma, on peut déterminer la densité du milieu. Les ondes à cette fréquence sont électrostatiques : elles sont constituées par un champ électrique qui oscille, sans champ magnétique - contrairement à des ondes électromagnétiques - et ne se propagent pas. Elles sont convectées par le milieu si celui-ci se déplace ; c'est donc par le biais de mesures in-situ que l'on peut les mesurer.
La fréquence plasma constitue une fréquence de coupure pour un milieu : en-dessous de cette fréquence les ondes ne se propagent plus.
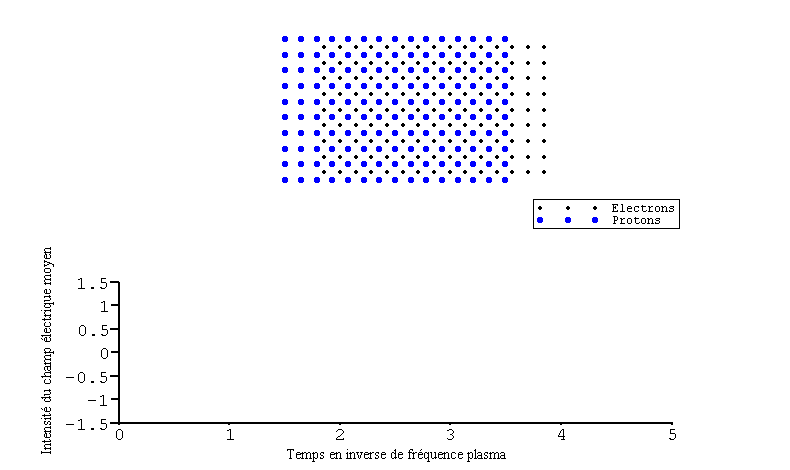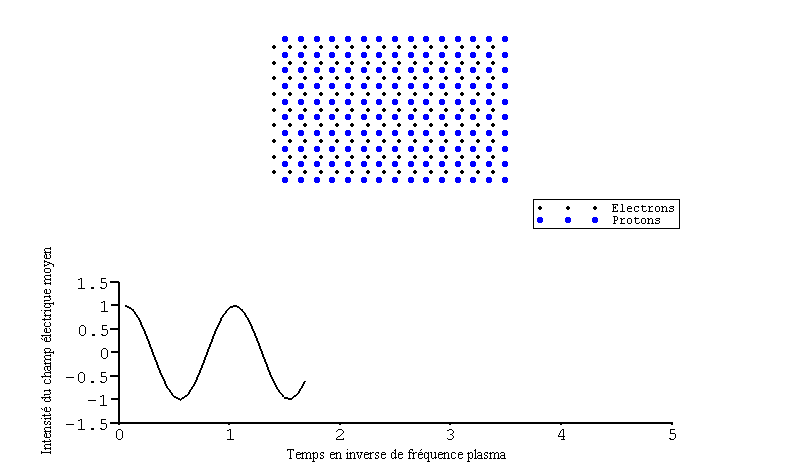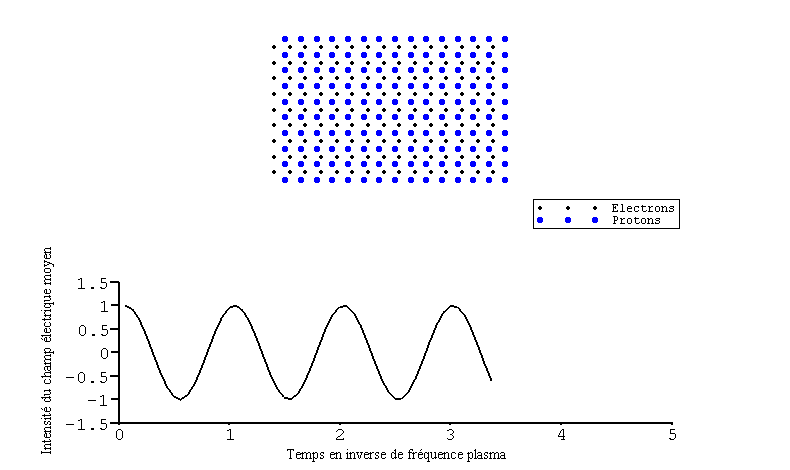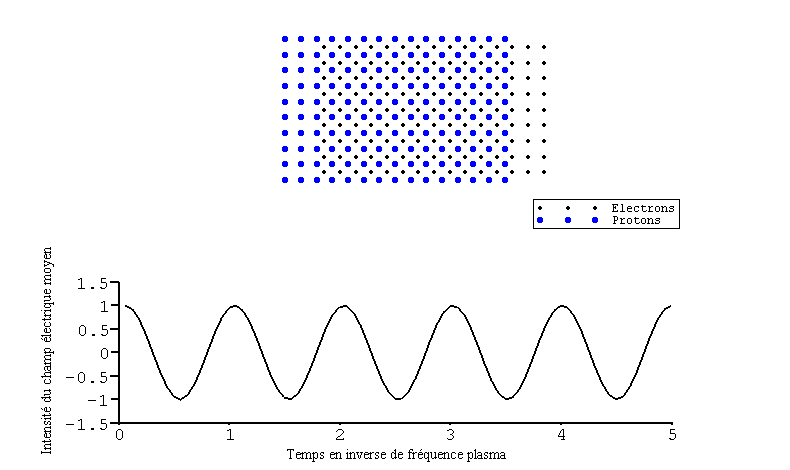
Cette figure montre le mouvement collectif des électrons suite à une perturbation électrostatique et le champ électrique moyen correspondant en fonction du temps. On y voit l'évolution périodique du système à la fréquence plasma.
Crédit :
Arnaud Beck - LESIA, Observatoire de Paris
Rayonnement cyclotron
En dehors de cette émission plasma, due au comportement collectif des particules accélérées, chaque particule émet du rayonnement à une fréquence 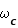 proportionnelle à l'intensité du champ magnétique :
proportionnelle à l'intensité du champ magnétique :
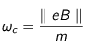
où 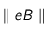 indique la norme du produit de la charge d'un électron et du champ magnétique. On appelle cela le rayonnement cyclotron qui se trouve être un rayonnement du domaine radio. La mesure de cette fréquence permet de déterminer le champ magnétique dans des régions où les méthodes spectroscopiques échouent (quand le champ magnétique est trop faible).
indique la norme du produit de la charge d'un électron et du champ magnétique. On appelle cela le rayonnement cyclotron qui se trouve être un rayonnement du domaine radio. La mesure de cette fréquence permet de déterminer le champ magnétique dans des régions où les méthodes spectroscopiques échouent (quand le champ magnétique est trop faible).
Rayonnement synchroton
Quand les particules émettrices de rayonnement cyclotron atteignent des vitesses non négligeables devant celle de lumière, la fréquence, et donc l'énergie, du rayonnement est augmentée d'un facteur 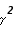 et on parle alors de rayonnement synchrotron.
et on parle alors de rayonnement synchrotron.

Avec 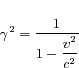
Où v est la vitesse de la particule émettrice et c la vitesse de la lumière. Étant donné la valeur du champ magnétique dans la couronne solaire et la vitesse des particules accélérées au cours d'une éruption, les sursauts synchrotrons solaires sont généralement observés dans le domaine centimétrique et millimétrique.

|

|
Energie de l'électron |
| 10 GHz |
3 cm |
1,5 MeV |
| 102 GHz |
3 mm |
3 MeV |
| 103 GHz |
0,3 mm |
13 MeV |
| 104 GHz |
0,3 mm |
44 MeV |
Tableau de correspondance entre la fréquence synchrotron (en GHz), la longueur d'onde équivalente, l'énergie des électrons (en MeV). Les valeurs sont données pour un champ magnétique de 500 Gauss.
Lors d'éruption particulièrement violentes, les particules peuvent atteindre des énergies très importantes (108 MeV) et être très relativistes. Le rayonnement synchroton obtenu est alors dans la gamme des rayons X et γ. Ce dernier rayonnement résulte également de transitions énergétiques dans le noyau (et non le cortège électronique) des atomes.
Rayonnement de freinage
Lorsqu'un électron s'approche d'un ion, il ressent son champ électrique et subit une accélération qui est d'autant plus grande que l'électron passe près de l'ion. S'il passe à une distance suffisament petite, l'accélération peut être assez violente pour provoquer une émission dans le domaine des rayons X appelée alors rayonnement de freinage (il est généralement nommé par son nom allemand : bremstrahlung).

Cette animation montre la trajectoire d'un électron (bleu) qui passe près d'un ion (rouge) et dont la trajectoire est violemment déviée sous l'effet du champ électrique ionique.
Crédit :
Arnaud Beck - LESIA, Observatoire de Paris
L'effet Doppler permet de recueillir des informations sur la vitesse globale des atomes à partir des raies spectrales. Quand un atome qui émet un photon à la longueur d'onde 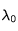 se déplace, la longueur d'onde observée
se déplace, la longueur d'onde observée 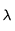 sera déplacée d'une quantité dépendant de cette vitesse V :
sera déplacée d'une quantité dépendant de cette vitesse V :
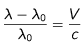
Les raies spectrales vont donc être décalées vers les grandes fréquences si l'objet observé s'approche de l'observateur et vers les fréquences plus petites si l'objet s'éloigne. La mesure du décalage spectral peut donc nous donner une information sur la vitesse de l'objet observé, le long de la ligne de visée. C'est aussi la technique utilisée pour mesurer le décalage vers le rouge des galaxies.
Un exemple de jet de matière

Sur cette image (longueur d'onde en abscisse, décroissante vers la droite, axe nord-sud solaire en ordonnée) obtenue avec le télescope THEMIS, on observe vers le haut un jet sombre s'étendant à gauche de l'imposante raie Hα de l'hydrogène. C'est la signature d'un jet de matière qui s'éloigne de nous, et donc tombe vers la surface du Soleil à une vitesse de plusieurs dizaines de kilomètres par seconde. Sur cette image, les raies fines observées sont des raies atmosphériques de la molécule d'eau. Elles peuvent donc servir à étalonner l'observation en longueur d'onde car elles ne subissent pas d'effet Doppler durant l'observation.
Crédit :
THEMIS - INSU (observation J. Aboudarham - C. Briand )
En présence d'un champ magnétique, certaines raies spectrales se retrouvent subdivisées en plusieurs raies fines et elles sont polarisées. La polarisation d'une raie signifie que le champ électrique de l'onde oscille en décrivant des figures spécifiques : cercle, segment de droite ou ellipse. La polarisation est alors circulaire, linéaire ou elliptique respectivement. Ce phénomène s'appelle l'effet Zeeman.
Illustration de l'effet Zeeman
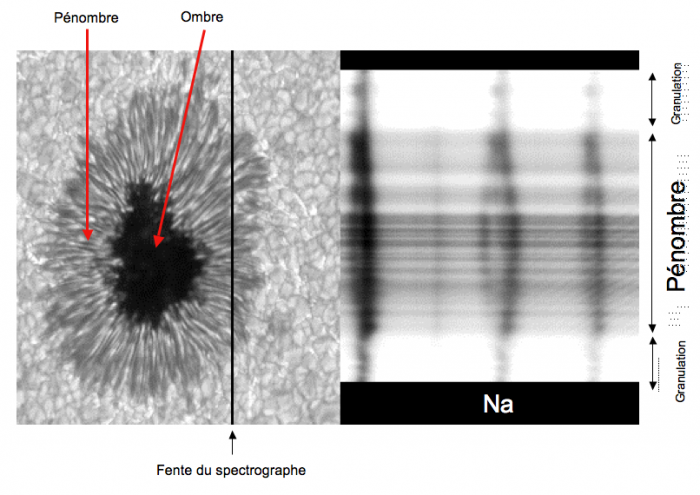
La figure de gauche est une image d'une tache solaire. La droite verticale indique la position de la fente du spectrographe ayant servi à sélectionner une partie du champ d'observation.
La figure de droite montre le spectre obtenu. On trouve la longueur d'onde en abscisse (horizontalement), et des positions sur le Soleil en ordonnée (verticalement). La raie centrale (sodium) est séparée en deux parties dans la zone de pénombre, là où le champ magnétique est non nul.
Crédit :
Kitt Peak Vacuum Telescope
Nous allons regarder un exemple restreint mais qui permet de comprendre comment les magnétogrammes sont obtenus.
Quand le champ magnétique est aligné avec la ligne de visée, la polarisation des ondes est circulaire. Les raies sont divisées en deux raies séparées de la longueur d'onde centrale 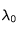 (celle en absence de champ magnétique) par :
(celle en absence de champ magnétique) par :
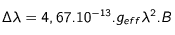 où
où 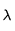 est la longueur d'onde (exprimée en Angstroem - 1 A = 0,1 nm), B est l'intensité du champ magnétique (exprimé en Gauss) et
est la longueur d'onde (exprimée en Angstroem - 1 A = 0,1 nm), B est l'intensité du champ magnétique (exprimé en Gauss) et 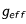 est appelé facteur de Landé. Ce facteur est caractéristique de la raie spectrale considérée.
est appelé facteur de Landé. Ce facteur est caractéristique de la raie spectrale considérée.
La séparation est donc d'autant plus grande que :
- la longueur d'onde est grande. Les raies infrarouges conduisent à une séparation spectrale plus grande que les raies dans le bleu ;
- le champ magnétique est fort ;
- le facteur de Landé est grand (la raie du fer à 6302.5 possède le plus grand facteur de Landé. Il vaut 2.5).
Nous avons vu qu'en observant plusieurs raies simultanément, on peut déduire des cartes de température, de densité, etc. en 3 dimensions. En couplant aussi des mesures de polarisation, on peut aussi dresser des cartes 3D du champ magnétique.
 Introduction
Introduction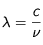
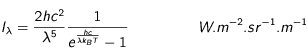
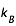 la constante de Boltzman (
la constante de Boltzman (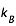 =1,38 10-23 J.K-1)
=1,38 10-23 J.K-1)

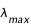 à la température de surfaceT :
à la température de surfaceT :
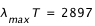 μm.K
μm.K

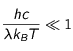
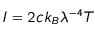
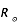 = 7 x 108 m
= 7 x 108 m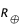 = 6,3 x 106 m
= 6,3 x 106 m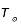 sachant que son pic d'émission (
sachant que son pic d'émission (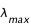 ) se situe à 500 nm. Même question pour la Terre
) se situe à 500 nm. Même question pour la Terre 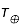 (
( 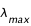 = 9,6 μm).
= 9,6 μm).
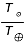 .
.
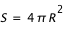 (avec R le rayon de la sphère).
(avec R le rayon de la sphère).
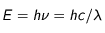
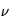 la fréquence et
la fréquence et 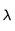 la longueur d'onde. Ainsi, plus la longueur d'onde est grande (fréquence petite) plus l'énergie du photon est petite.
la longueur d'onde. Ainsi, plus la longueur d'onde est grande (fréquence petite) plus l'énergie du photon est petite.


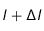 peut-on espérer à la sortie de notre tranche de plasma ? Quelle forme aura le profil de la raie qui nous intéresse ?
peut-on espérer à la sortie de notre tranche de plasma ? Quelle forme aura le profil de la raie qui nous intéresse ?

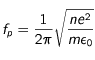
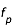 la fréquence plasma (en Hz),
la fréquence plasma (en Hz), 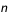 est la densité d'électrons,
est la densité d'électrons, 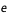 la charge élémentaire (1,6 x 10-19 c),
la charge élémentaire (1,6 x 10-19 c), 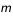 la masse de l'électron (9 x 10-31kg),
la masse de l'électron (9 x 10-31kg), 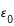 la constante diélectrique (8,8 x 10-12 F. m-1).
la constante diélectrique (8,8 x 10-12 F. m-1).
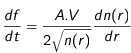
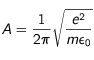 , V la vitesse du faisceau d'électrons, n(r) un modèle de densité électronique en fonction de la distance au Soleil et dn(r)/dr la variation de cette densité en fonction de la distance au Soleil. Donc, si l'on se donne un modèle de densité électronique dans le milieu interplanétaire, on peut déduire V à partir de la mesure de pente df/dt.
, V la vitesse du faisceau d'électrons, n(r) un modèle de densité électronique en fonction de la distance au Soleil et dn(r)/dr la variation de cette densité en fonction de la distance au Soleil. Donc, si l'on se donne un modèle de densité électronique dans le milieu interplanétaire, on peut déduire V à partir de la mesure de pente df/dt.
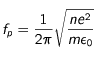
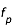 la fréquence plasma (en Hz),
la fréquence plasma (en Hz), 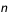 est la densité d'électrons,
est la densité d'électrons, 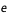 la charge élémentaire (1,6 x 10-19 c),
la charge élémentaire (1,6 x 10-19 c), 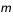 la masse de l'électron (9 x 10-31kg),
la masse de l'électron (9 x 10-31kg), 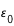 la constante diélectrique (8,8 x 10-12 F. m-1). Si on peut mesurer la fréquence plasma, on peut déterminer la densité du milieu. Les ondes à cette fréquence sont électrostatiques : elles sont constituées par un champ électrique qui oscille, sans champ magnétique - contrairement à des ondes électromagnétiques - et ne se propagent pas. Elles sont convectées par le milieu si celui-ci se déplace ; c'est donc par le biais de mesures in-situ que l'on peut les mesurer.
la constante diélectrique (8,8 x 10-12 F. m-1). Si on peut mesurer la fréquence plasma, on peut déterminer la densité du milieu. Les ondes à cette fréquence sont électrostatiques : elles sont constituées par un champ électrique qui oscille, sans champ magnétique - contrairement à des ondes électromagnétiques - et ne se propagent pas. Elles sont convectées par le milieu si celui-ci se déplace ; c'est donc par le biais de mesures in-situ que l'on peut les mesurer.

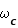 proportionnelle à l'intensité du champ magnétique :
proportionnelle à l'intensité du champ magnétique :
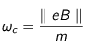
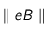 indique la norme du produit de la charge d'un électron et du champ magnétique. On appelle cela le rayonnement cyclotron qui se trouve être un rayonnement du domaine radio. La mesure de cette fréquence permet de déterminer le champ magnétique dans des régions où les méthodes spectroscopiques échouent (quand le champ magnétique est trop faible).
indique la norme du produit de la charge d'un électron et du champ magnétique. On appelle cela le rayonnement cyclotron qui se trouve être un rayonnement du domaine radio. La mesure de cette fréquence permet de déterminer le champ magnétique dans des régions où les méthodes spectroscopiques échouent (quand le champ magnétique est trop faible).
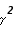 et on parle alors de rayonnement synchrotron.
et on parle alors de rayonnement synchrotron.

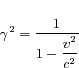



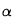
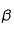
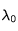 se déplace, la longueur d'onde observée
se déplace, la longueur d'onde observée 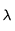 sera déplacée d'une quantité dépendant de cette vitesse V :
sera déplacée d'une quantité dépendant de cette vitesse V :
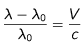


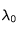 (celle en absence de champ magnétique) par :
(celle en absence de champ magnétique) par :
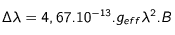 où
où 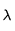 est la longueur d'onde (exprimée en Angstroem - 1 A = 0,1 nm), B est l'intensité du champ magnétique (exprimé en Gauss) et
est la longueur d'onde (exprimée en Angstroem - 1 A = 0,1 nm), B est l'intensité du champ magnétique (exprimé en Gauss) et 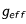 est appelé facteur de Landé. Ce facteur est caractéristique de la raie spectrale considérée.
est appelé facteur de Landé. Ce facteur est caractéristique de la raie spectrale considérée.