Cette section traite plus spécialement de questions spécifiques à l'astronomie, liées au fait que le lieu d'observation, la Terre, a la fâcheuse habitude de tourner !
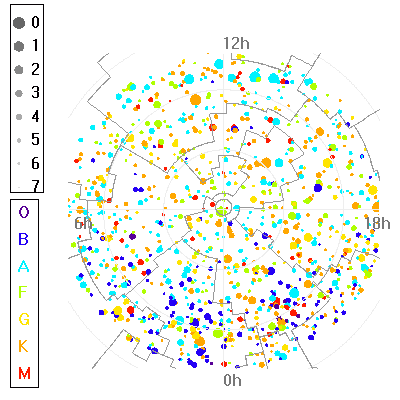
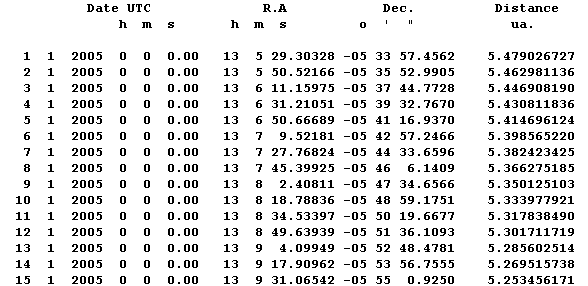
Les cartes et les éphémérides donnent les positions des objets dans des coordonnées particulières, le plus souvent les coordonnées équatoriales.
Dans un système d'axes liés à la Terre, avec un axe parallèle à l'axe polaire et un autre perpendiculaire, on travaille en coordonnées équatoriales, comme avec un télescope en monture équatoriale. Un cas particulier de monture équatoriale est la monture en berceau, utilisée pour la plupart des grands instruments de la classe 4-mètres construits dans les années 1970-80.
Les coordonnées locales servent au pointage d'un télescope en monture azimutale : l'un des axes est selon la verticale locale, l'autre lui est perpendiculaire. Pour des raisons techniques, les grands télescopes récents ont tous une monture azimutale.
ObjectifsIllustrer les référentiels utilisés, munis de leurs repères, et y définir les coordonnées des objets.
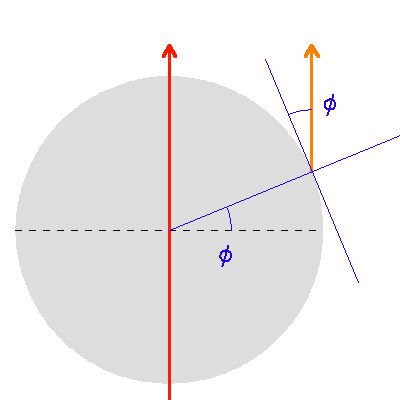
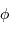, cet axe est incliné de 
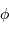par rapport à l'horizontale (si l'on néglige l'aplatissement de la Terre).
Si l'on se repère dans un système d'axes liés à la Terre, avec un axe parallèle à l'axe polaire, et un autre perpendiculaire, on travaille en coordonnées équatoriales, comme un télescope en monture équatoriale.
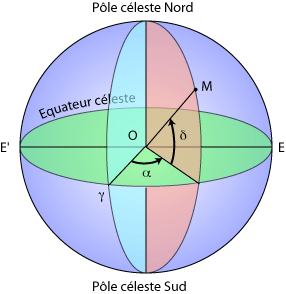
Les coordonnées équatoriales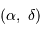 
ne dépendent pas du lieu d'observation. Ce sont elles qui sont données par les catalogues d'objets ou les éphémérides. L'origine des ascensions droites est le point vernal. La déclinaison est nulle sur l'équateur céleste.
Si l'on se repère par rapport au zénith et à l'horizon local, qui n'est qu'une extension du référentiel du laboratoire, les coordonnées locales permettront de rendre compte de l'élévation d'un astre, et de sa position par
rapport au méridien. Ces coordonnées, azimut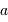 
, hauteur 
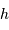, servent au pointage d'un télescope en monture azimutale.
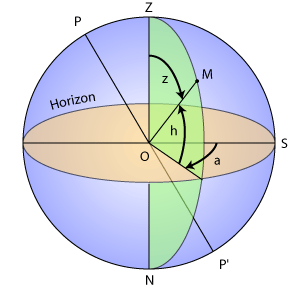
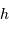et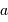 
, hauteur et azimut, sont repérés par rapport à des axes horizontaux et verticaux.
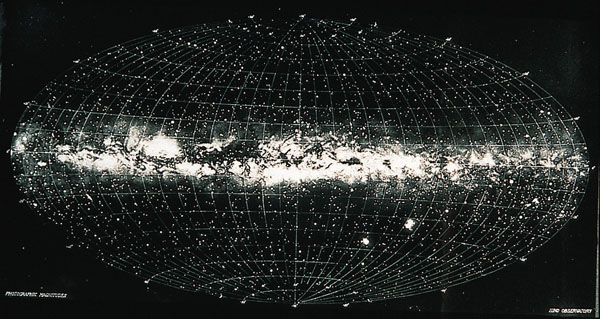
Les coordonnées galactiques sont définies par rapport au plan de la galaxie. Elles sont évidemment bien utiles pour décrire notre galaxie, mais également pour se repérer dans le ciel profond. Il est en effet plus facile d'observer le ciel profond au voisinage des pôles galactiques, moins encombrés par les objets de la galaxie.
Le choix de la monture n'est pas sans incidence sur l'observation. Une monture équatoriale permet de suivre un champ sans rotation de champ, car elle fige la rotation totalement, contrairement à une monture azimutale. En effet, cette dernière propose une translation du champ, autour de l'objet central, parallèlement à l'horizon terrestre, et non le long d'une ligne d'égale déclinaison.
Les 2 animations illustrent ceci, en modélisant l'observation d'un même champ stellaire avec un collecteur sur monture équatoriale ou azimutale.
Trigonométrie sphériqueDifficulté : ☆ Temps : 30 min
Un peu de trigonométrie sphérique nous apprend que la distance angulaire entre 2 objets A et B de coordonnées équatoriales respectives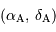 
et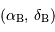 
s'écrit :
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation10.png)
Vérifier cette expression dans le cas particulier où A et B sont 2 objets sur l'équateur céleste.
[1 points]
Vérifier cette expression dans le cas particulier où A et B ont même ascension droite.
[2 points]
Vérifier cette expression dans le cas particulier où A et B sont séparés de 12 h en ascension droite. Préciser le résultat lorsque, en plus, les déclinaisons sont égales.
[3 points]
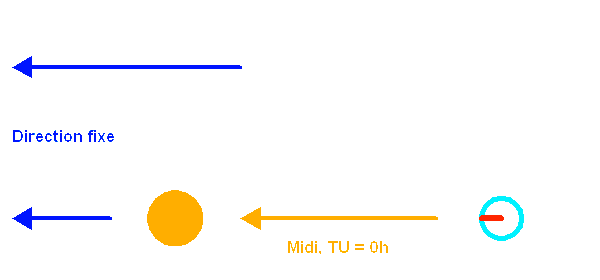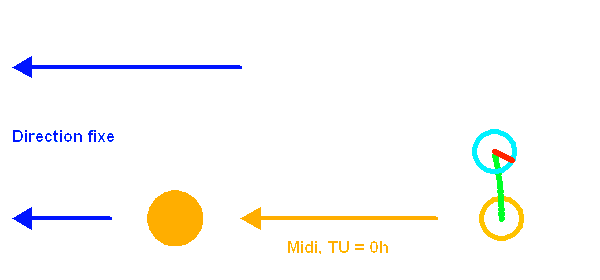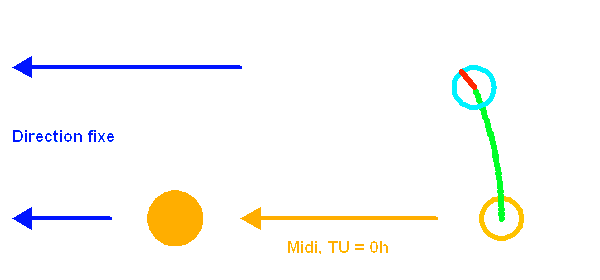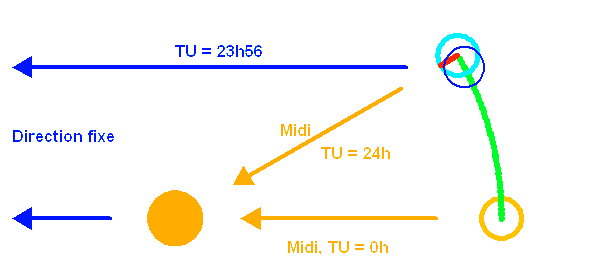
La rotation de la Terre autour du Soleil se combine à sa rotation propre pour définir la durée de 24 heures entre deux passages du Soleil au méridien.
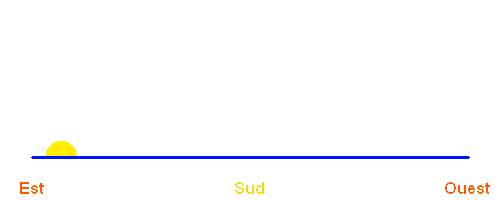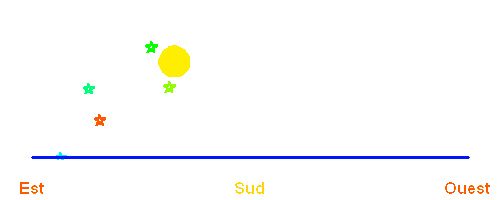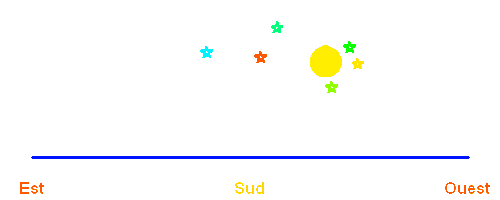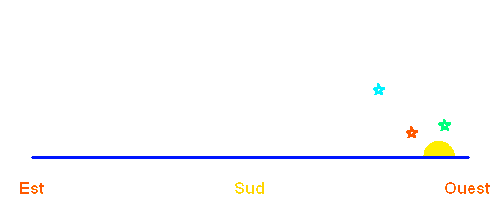
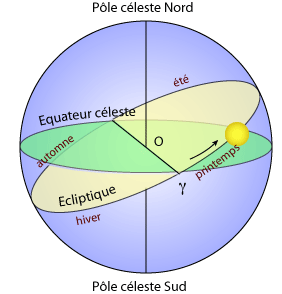
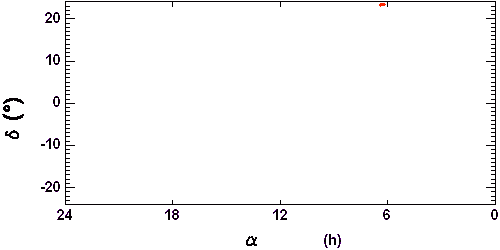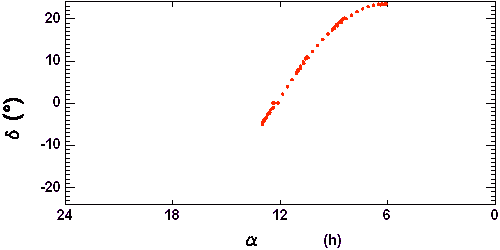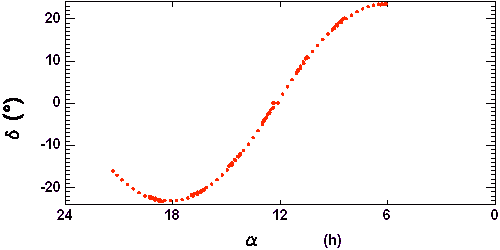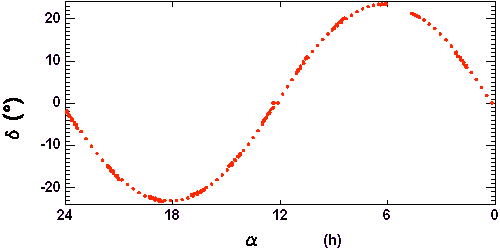
La révolution de la Terre autour du Soleil entraîne le déplacement apparent de celui-ci par rapport aux étoiles, déplacement que l'on ne perçoit pas directement... sauf si l'on éteint un peu le soleil (on pourrait aussi souffler l'atmosphère).
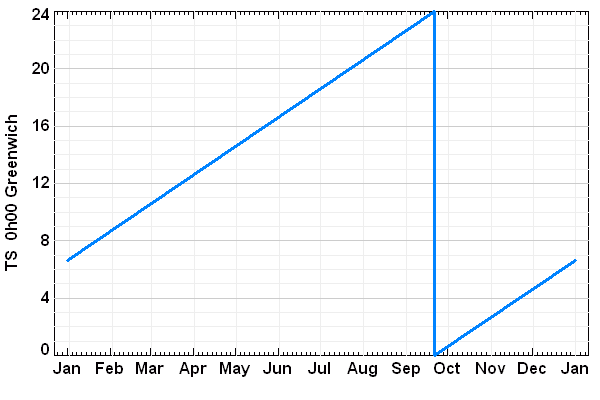
Le temps sidéral, qui donne l'ascension droite d'une étoile culminant à minuit, varie de 24 h sur l'année. L'origine est à l'équinoxe de printemps.
ObjectifsComment savoir si une étoile est visible ou non ? Il faut connaître le temps des étoiles.
C'est le Soleil qui définit le jour et la nuit. Mais comme la Terre tourne autour du Soleil, cette alternance jour/nuit n'est pas en phase avec les étoiles. Le temps sidéral, qui est plus à considérer comme un angle sidéral que comme un temps, permet de se repérer indépendamment du mouvement de rotation autour de la Terre.
Le temps sidéral, c'est, littéralement, le temps des étoiles, et non celui du Soleil. Si le passage du soleil définit, entre 2 midis successifs, la journée moyenne de 24 h, celui des étoiles définit une autre "journée" de seulement 23 heures et 56 minutes en temps solaire, mais 24h00 en temps sidéral.
Définition du temps sidéralLe temps sidéral est l'angle horaire entre le méridien sud et le point vernal.
De cette définition, on retient que le temps sidéral est plutôt une position angulaire qu'un temps. Il se note comme une ascension droite, en h, min et s. Mais comme la définition n'est pas très pratique, on peut donner un équivalent de définition.
'Définition pratique' du temps sidéralLe temps sidéral est l'ascension droite des objets qui passent au méridien à un instant donné.
De cette définition, on retient que le temps sidéral est plutôt une position angulaire qu'un temps. Il se note comme une ascension droite, en h, min et s. Mais comme la définition n'est pas très pratique, on peut donner un équivalent de définition.
Les étoiles reviennent en une même position en 23h56min04s. Les 236 secondes manquantes par jour, cumulés sur un an, représentent 24 heures, soit l'équivalent d'une rotation, celle que la Terre a fait par rapport aux étoiles mais pas par rapport au Soleil.
Jour, heure, minutes et seconde sidérales ne valent pas leurs équivalents solaires. Le rapport vaut 366.25/365.25
| Temps sidéral | Temps solaire |
|---|---|
| 24h00 | 23h56min |
| 24h04 | 24h00min |
| 1.002738 s sidérale | 1 s solaire |
| 1 s sidérale | 0.997269 s solaire |
L'angle horaire d'un astre repère sa position par rapport au méridien. Une étoile de déclinaison nulle de lève avec un angle horaire de -6 h, et se couche à +6 h. A angle horaire nul, elle passe au méridien et culmine.
En pratique, le temps sidéral, exprimé en heure et minute, correspond à l'ascension droite d'un objet dans le plan méridien. Les éphémérides définissent le temps sidérale par les coordonnées.... du Soleil.
La relation entre l'ascension droit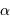e 
d'une étoile, son
angle horaire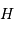 
et le temps sidéral 
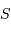s'exprime :
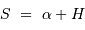
L'angle horaire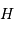 
est nul au méridien, et donc un astre culmine au méridien lorsque son ascension droite vérifie :
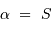
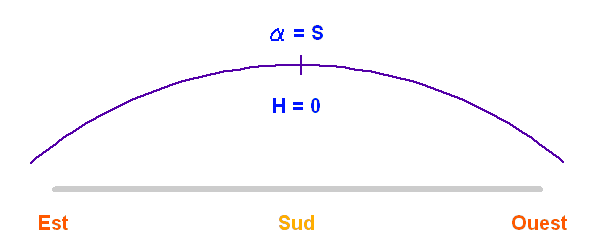
QCMObjectifsComment calculer le temps sidéral.
Les éphémérides du Soleil donnent le temps sidéral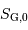 
à 0h00 TU à Greenwich.
On en déduit le temps sidéral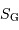 
, toujours à Greenwich, mais à toute heure TU du temps universel
en augmentant le temps sidéral de TU à un facteur près ; ce facteur rend compte de la différence entre 24h00 et 23h56.
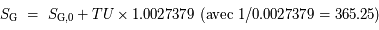
L'origine du temps sidéral est à minuit à l'équinoxe d'automne. Chaque jour, le temps sidéral prend environ 4 minutes d'avance sur le temps universel.
On passe ensuite au temps sidéral en tout lieu en la retranchant au temps sidéral à Greenwich la longitude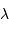 
du lieu d'observation :
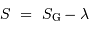
Cette équation signifie que le temps sidéral dépend intimement du lieu d'observation. A un instant donné, chacun voit minuit à sa porte : les étoiles qui culminent au méridien dépendent du lieu d'observation, et donc le temps sidéral est partout différent (sauf pour les lieux de même longitude). Néanmoins, le temps sidéral correspondant au passage au méridien d'une étoile donnée est par définition le même en tout lieu. Par exemple : une étoile va culminer à Strasbourg (longitude 7°45' est) ou Brest (4°30' ouest) à même temps sidéral, mais ce passage au méridien va survenir environ 49 minutes plus tardivement à Brest. Entre ces deux dates, le temps sidéral à Greenwich aura dérivé de 8 s par rapport au temps universel.
Le tableau ci-dessous donne l'évolution du temps sidéral à Greenwich à 0h00, au cours de l'année 1997 (données de l'IMCCE).
S'en servir pour déterminer le temps sidéral à toute date.
QCMQuand demander du temps de télescope ?Difficulté : ☆☆ Temps : 30min
Un observateur souhaite obtenir du temps de télescope à l'ESO (observatoire austral européen). Les appels d'offres sont ouverts chaque semestre, pour des observations courant respectivement du 1er avril au 30 septembre, puis du 1er octobre au 31 mars. Il faut choisir des cibles en conséquence.
Le programme d'observation requiert des cibles visibles toute la nuit. Traduire cette condition en une relation entre l'ascension droite de la cible et le temps sidéral à minuit.
[2 points]
Quelles cibles (définies par leur ascension droite) seront observable au semestre 01/04-30/09 ?
[1 points]
Un autre observatoire propose des semestres d'observation du 1er mars au 31 août, puis 1er septembre au 28 février. Comment est modifié le résultat ?
[1 points]
ObjectifsLa mesure de la période d'un phénomène dépend du référentiel.
Selon le point de vue, vu de la Terre ou du Soleil, un phénomène périodique ne présentera pas la même période.
Un phénomène sidéral est décrit dans le référentiel héliocentrique. Il se repère en pratique sur un fond d'étoiles, fixe.
Un phénomène synodique est décrit dans un référentiel lié à la Terre, mais non géocentrique. Il se repère par rapport à un système d'axes dont l'un pointe en permanence vers le Soleil.
C'est évidemment la définition du jour moyen (24 h en moyenne s'écoulant entre deux passages successifs du Soleil au méridien) qui impose le point de vue synodique.
Entre les points de vue sidéral et synodique, il y a donc un désaccord d'un tour par an !
La période de révolution sidérale de Jupiter est de l'ordre de 12 ans : une révolution complète de Jupiter autour du Soleil dure 12 ans. Pratiquement, l'ascension droite de Jupiter va évoluer de 360 deg en 12 ans. Observé de la Terre, Jupiter va mettre 12 ans pour revenir dans une constellation donnée.
Mais la période de révolution synodique de Jupiter est de 13 mois seulement. Si à une date donnée, Jupiter est à l'opposition, il s'écoulera 13 mois avant l'opposition suivante. Au bout de 13 mois, Jupiter à l'opposition sera dans une constellation différente, à environ 30 deg (360/12) de la précédente.
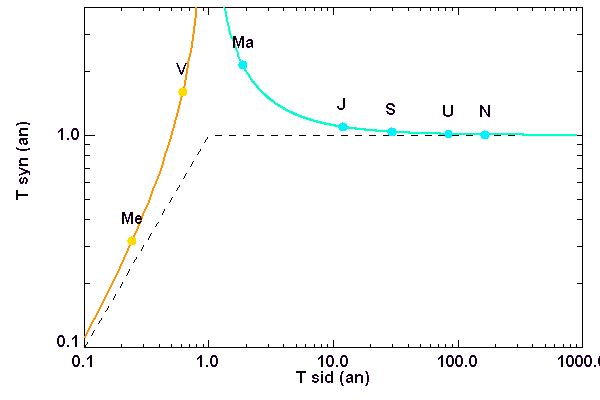
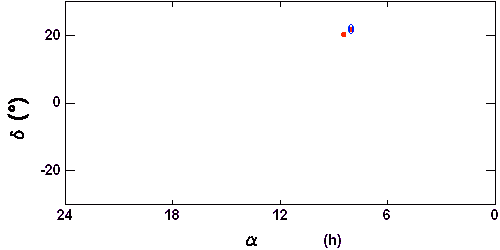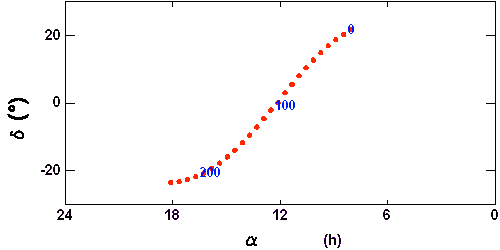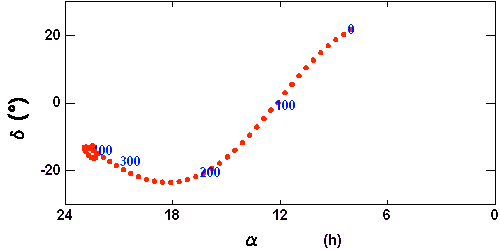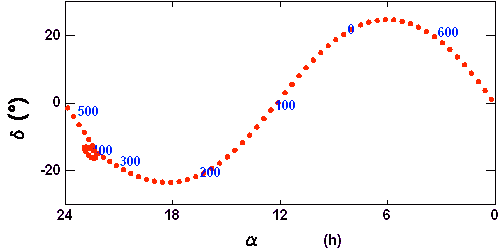
QCMTemps des étoiles, temps mesuré depuis la Terre... il est important de s'y retrouver. De manière générale, une mesure depuis la Terre sera synodique ; mais une loi physique s'exprimera avec une grandeur sidérale.
Retenir du temps sidéral que c'est un angle plus qu'un temps.
pages_temps-sideral/temps-sideral-sexercer.html
pages_temps-sideral-determination/temps-sideral-determination-sexercer.html
pages_periode-sideral-synodique/periode-sideral-synodique-sexercer.html
pages_reperes/referentiel-sexercer.html
Dans ce cas, les déclinaisons sont nulles toutes les deux.
Un peu de trigonométrie :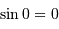 
et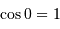 
.
Un peu plus de trigonométrie : comme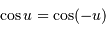 
, 
.
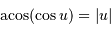Les déclinaisons de A et B étant toutes deux nulles, la relation se réécrit simplement :
![d = {\mathrm{acos}} \left[\cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation15.png)
D'où la solution, évidemment simple :
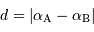
Peut-être est-il utile de rappeler que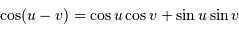 
Avec des ascensions droites égales, la distance angulaire se réécrit :
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation18.png)
Plus simplement :
![d = {\mathrm{acos}} \left[ \cos( \delta _{\mathrm{A}} - \delta _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation19.png)
Soit
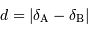
Là encore, le résultat est assez intuitif
Que devient dans ce cas la contribution du terme avec les ascensions droites ?
Encore un peu de trigonométrie :
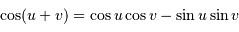
Moins courant, mais un cercle trigonométrique le justifie aisément :
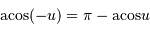
La solution
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation23.png)
s'écrit dans ce cas, avec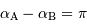 
.
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} - \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right] = \pi - {\mathrm{acos}} \left[ \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} - \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation25.png)
Et donc, dans ce cas :
![d = \pi - {\mathrm{acos}} [ \cos ( \delta _{\mathrm{A}} + \delta _{\mathrm{B}}) ] = \pi - | \delta _{\mathrm{A}} + \delta _{\mathrm{B}}|](../pages_reperes/equations_referentiel/equation26.png)
Si, de plus, les déclinaisons sont égales, on trouve alors
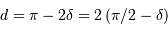
La distance angulaire, en passant par les pôles, est bien égale à 2 fois la colatitude ; la colatitude est le complément à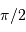 
(ou 90 deg) de la latitude.