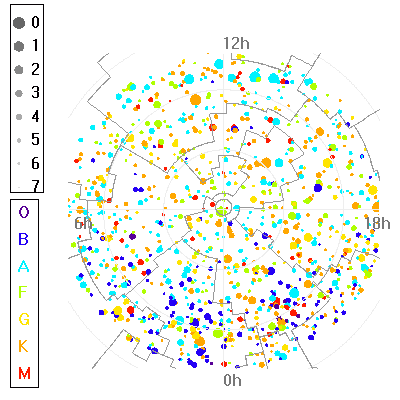
Carte du ciel, autour de l'étoile polaire. Les méridiens convergent au pôle nord. Les cercles sont des lignes d'iso-déclinaison.
Crédit :
BSC/ASM
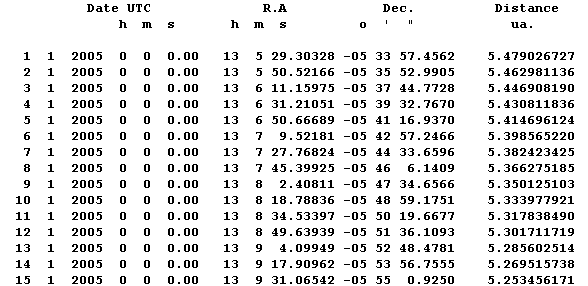
Éphéméride sur 15 jours de Jupiter. L'ascension droite (RA = right ascension) et la déclinaison sont données en fonction du temps universel UTC.
Crédit :
IMCCE
Cartes et éphémérides
Les cartes et les éphémérides donnent les positions des objets dans des coordonnées particulières, le plus souvent les coordonnées équatoriales.
Monture équatoriale

L'axe polaire de la monture équatoriale pointe vers le nord ; son inclinaison dépend donc de la latitude du lieu d'observation. L'axe de déclinaison lui est perpendiculaire.
Ex: grande lunette de l'observation de Poulkovo (Saint-Pétersbourg, Russie).
Crédit :
Bibliothèque de l'Observatoire de Paris-Meudon
Monture équatoriale en berceau

Monture équatoriale en berceau. L'axe équatorial, dans le plan de l'image, est matérialisé côté nord par une forme en fer à cheval ; l'axe de déclinaison est perpendiculaire au plan de l'image.
Crédit :
CFHT
Monture équatoriale
Dans un système d'axes liés à la Terre, avec un axe parallèle à l'axe polaire et un autre perpendiculaire, on travaille en coordonnées équatoriales, comme avec un
télescope en monture équatoriale. Un cas particulier de monture équatoriale est la monture en berceau, utilisée pour la plupart des grands instruments de la classe 4-mètres construits dans les années 1970-80.
Monture azimutale

Les axes d'une monture azimutale sont simplement verticaux et horizontaux. Tous les grands télescopes sont aujourd'hui tous construits avec une telle monture. Le bâtiment tourne avec le télescope pour le pointage en azimut.
Crédit :
ESO
Monture azimutale
Les coordonnées locales servent au pointage d'un
télescope en monture azimutale : l'un des axes est selon la verticale locale, l'autre lui est perpendiculaire. Pour des raisons techniques, les grands télescopes récents ont tous une monture azimutale.
 Objectifs
Objectifs
Illustrer les référentiels utilisés, munis de leurs repères, et y définir les coordonnées des objets.
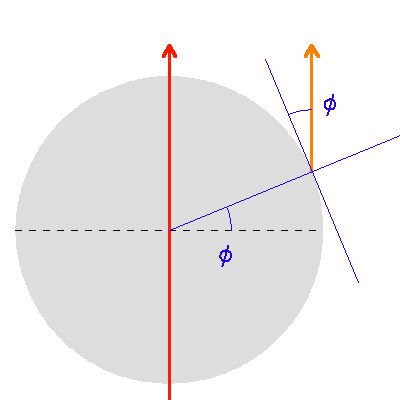
L'axe horaire (flèche orange) d'une monture équatoriale est parallèle à l'axe de rotation de la Terre (flèche rouge). En un lieu de latitude
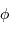
, cet axe est incliné de
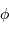
par rapport à l'horizontale (si l'on néglige l'
aplatissement de la Terre).
Crédit :
ASM
Ascension droite et déclinaison
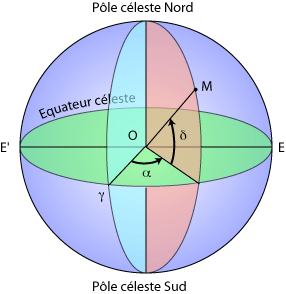
Coordonnées équatoriales : ascension droite, repérée à partir du
point vernal, et déclinaison, par rapport à l'équateur céleste.
Crédit :
ASM
Point vernal
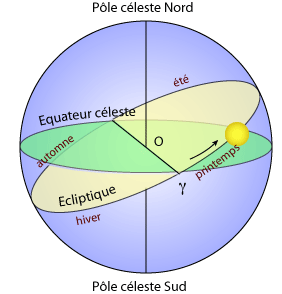
Le point vernal est à l'intersection de l'
écliptique et de l'équateur céleste, côté printemps.
Crédit :
ASM
Les coordonnées équatoriales 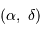 ne dépendent pas du lieu d'observation. Ce sont elles qui sont données par les catalogues d'objets ou les éphémérides. L'origine des ascensions droites est le point vernal. La déclinaison est nulle sur l'équateur céleste.
ne dépendent pas du lieu d'observation. Ce sont elles qui sont données par les catalogues d'objets ou les éphémérides. L'origine des ascensions droites est le point vernal. La déclinaison est nulle sur l'équateur céleste.
Référentiel local
Si l'on se repère par rapport au zénith et à l'horizon local, qui n'est qu'une extension du référentiel du laboratoire, les coordonnées locales permettront de rendre compte de l'élévation d'un astre, et de sa position par
rapport au méridien. Ces coordonnées, azimut 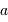 , hauteur
, hauteur 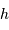 , servent au pointage d'un télescope en monture azimutale.
, servent au pointage d'un télescope en monture azimutale.
Coordonnées locales
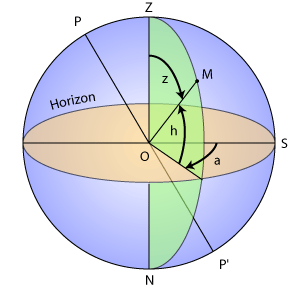
Les angles
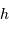
et
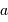
, hauteur et azimut, sont repérés par rapport à des axes horizontaux et verticaux.
Crédit :
ASM
Référentiel galactique
Les coordonnées galactiques sont définies par rapport au plan de la galaxie. Elles sont évidemment bien utiles pour décrire notre galaxie, mais également pour se repérer dans le ciel profond. Il est en effet plus facile d'observer le ciel profond au voisinage des pôles galactiques, moins encombrés par les objets de la galaxie.
Coordonnées galactiques
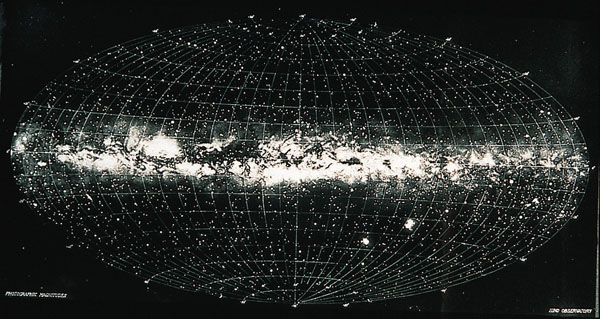
Représentation de la carte du ciel, en coordonnées galactiques. La Voie Lactée s'étend de part et d'autre de l'équateur galactique. Cet équateur est le support de la longitude galactique, la latitude galactique mesurant l'éloignement à la Voie Lactée.
Crédit :
Observatoire de Paris

Pas de rotation apparente du champ avec une monture équatoriale. Le champ se déplace parallèlement à une ligne d'égale déclinaison : les cibles sont figées dans le champ.
Crédit :
ASM

Avec une monture azimutale, le champ se translate par rapport à l'horizon, ce qui conduit à une rotation apparente des cibles.
Crédit :
ASM
Rotation du champ
Le choix de la monture n'est pas sans incidence sur l'observation. Une monture équatoriale permet de suivre un champ sans rotation de champ, car elle fige la rotation totalement, contrairement à une monture azimutale. En effet, cette dernière propose une translation du champ, autour de l'objet central, parallèlement à l'horizon terrestre, et non le long d'une ligne d'égale déclinaison.
Les 2 animations illustrent ceci, en modélisant l'observation d'un même champ stellaire avec un collecteur sur monture
équatoriale ou
azimutale.
 Trigonométrie sphérique
Trigonométrie sphérique
Difficulté : ☆
Temps : 30 min
Un peu de trigonométrie sphérique nous apprend que la distance angulaire entre 2 objets A et B de coordonnées équatoriales respectives 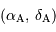 et
et 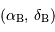 s'écrit :
s'écrit :
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation10.png)
Question 1)
Vérifier cette expression dans le cas particulier où A et B sont 2 objets sur l'équateur céleste.
[1 points]
Dans ce cas, les déclinaisons sont nulles toutes les deux.
Un peu de trigonométrie : 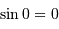 et
et 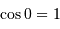 .
.
Un peu plus de trigonométrie : comme 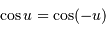 ,
, 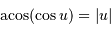 .
.
Question 2)
Vérifier cette expression dans le cas particulier où A et B ont même ascension droite.
[2 points]
Peut-être est-il utile de rappeler que 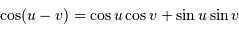
Question 3)
Vérifier cette expression dans le cas particulier où A et B sont séparés de 12 h en ascension droite. Préciser le résultat lorsque, en plus, les déclinaisons sont égales.
[3 points]
Que devient dans ce cas la contribution du terme avec les ascensions droites ?
Encore un peu de trigonométrie :
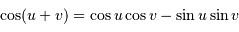
Moins courant, mais un cercle trigonométrique le justifie aisément :
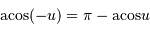
- Question 1
Aide :
Dans ce cas, les déclinaisons sont nulles toutes les deux.
Aide :
Un peu de trigonométrie : 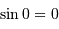 et
et 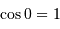 .
.
Aide :
Un peu plus de trigonométrie : comme 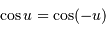 ,
, 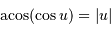 .
.
Solution :
Les déclinaisons de A et B étant toutes deux nulles, la relation se réécrit simplement :
![d = {\mathrm{acos}} \left[\cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation15.png)
D'où la solution, évidemment simple :
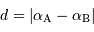
- Question 2
Aide :
Peut-être est-il utile de rappeler que 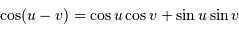
Solution :
Avec des ascensions droites égales, la distance angulaire se réécrit :
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation18.png)
Plus simplement :
![d = {\mathrm{acos}} \left[ \cos( \delta _{\mathrm{A}} - \delta _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation19.png)
Soit
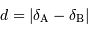
Là encore, le résultat est assez intuitif
- Question 3
Aide :
Que devient dans ce cas la contribution du terme avec les ascensions droites ?
Aide :
Encore un peu de trigonométrie :
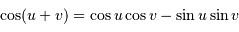
Aide :
Moins courant, mais un cercle trigonométrique le justifie aisément :
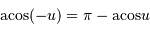
Solution :
La solution
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation23.png)
s'écrit dans ce cas, avec 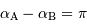 .
.
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} - \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right] = \pi - {\mathrm{acos}} \left[ \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} - \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation25.png)
Et donc, dans ce cas :
![d = \pi - {\mathrm{acos}} [ \cos ( \delta _{\mathrm{A}} + \delta _{\mathrm{B}}) ] = \pi - | \delta _{\mathrm{A}} + \delta _{\mathrm{B}}|](../pages_reperes/equations_referentiel/equation26.png)
Si, de plus, les déclinaisons sont égales, on trouve alors
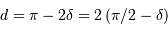
La distance angulaire, en passant par les pôles, est bien égale à 2 fois la colatitude ; la colatitude est le complément à 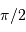 (ou 90 deg) de la latitude.
(ou 90 deg) de la latitude.






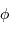 , cet axe est incliné de
, cet axe est incliné de 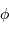 par rapport à l'horizontale (si l'on néglige l'
par rapport à l'horizontale (si l'on néglige l'

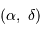 ne dépendent pas du lieu d'observation. Ce sont elles qui sont données par les catalogues d'objets ou les éphémérides. L'origine des ascensions droites est le
ne dépendent pas du lieu d'observation. Ce sont elles qui sont données par les catalogues d'objets ou les éphémérides. L'origine des ascensions droites est le 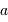 , hauteur
, hauteur 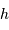 , servent au pointage d'un
, servent au pointage d'un 
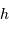 et
et 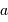 , hauteur et azimut, sont repérés par rapport à des axes horizontaux et verticaux.
, hauteur et azimut, sont repérés par rapport à des axes horizontaux et verticaux.



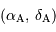 et
et 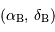 s'écrit :
s'écrit :
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation10.png)
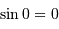 et
et 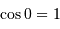 .
.
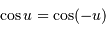 ,
, 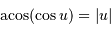 .
.
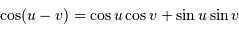
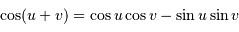
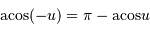
![d = {\mathrm{acos}} \left[\cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation15.png)
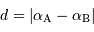
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation18.png)
![d = {\mathrm{acos}} \left[ \cos( \delta _{\mathrm{A}} - \delta _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation19.png)
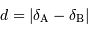
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation23.png)
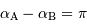 .
.
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} - \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right] = \pi - {\mathrm{acos}} \left[ \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} - \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation25.png)
![d = \pi - {\mathrm{acos}} [ \cos ( \delta _{\mathrm{A}} + \delta _{\mathrm{B}}) ] = \pi - | \delta _{\mathrm{A}} + \delta _{\mathrm{B}}|](../pages_reperes/equations_referentiel/equation26.png)
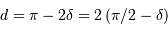
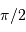 (ou 90 deg) de la latitude.
(ou 90 deg) de la latitude.