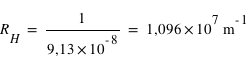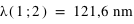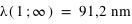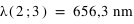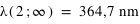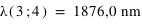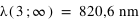L'analyse de la lumière émise ou absorbée par les atomes d'un gaz nous renseigne sur la composition, la température et la densité de ce gaz. Cette analyse de la lumière en ses différentes longueurs d'ondes constitue ce qu'on appelle la spectroscopie.
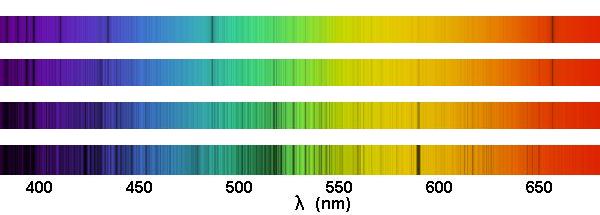
Spectres stellaires, pour des étoiles de température effective de 4000 à 7000 K.
Crédit :
ASM
Spectre continu
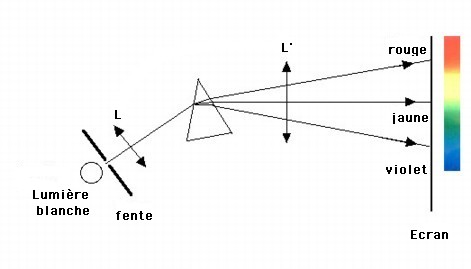
Lorsque l'on décompose la lumière blanche du Soleil à l'aide d'un prisme on observe un évantail de couleurs. On dit que la lumière blanche possède un spectre continu, car on passe d'une couleur à une autre sans interruption dans la succession des couleurs.
Crédit :
Observatoire de Paris
Expérimentalement on constate que tout corps (gazeux ou solide) sous haute pression et à haute température, donne naissance à un spectre continu de lumière.
Spectre de raies d'émission
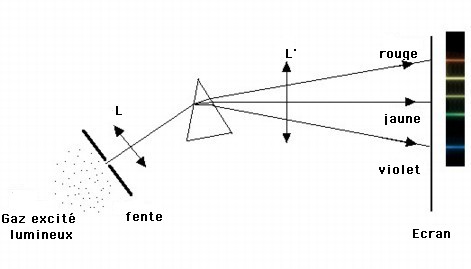
Si on analyse la lumière émise par une lampe à vapeur de sodium (gaz peu dense et chaud) à l'aide d'un prisme, on constate que le spectre de la lumière émise est constitué de deux raies fines très intenses dans la partie jaune du spectre, se détachant sur fond noir. Le spectre obtenu est discontinu et il est constitué d'un nombre limité de radiations.
Un gaz, à basse pression et à température élevée, émet une lumière constituée d'un nombre restreint de radiations : on obtient un spectre de raies d'émission.
Crédit :
Observatoire de Paris
Les couleurs et les positions des raies dans le spectre sont caractéristiques des atomes du gaz qui émettent ces radiations, autrement dit chaque élément chimique à l'état gazeux possède son propre spectre de raies.
Spectre d'absorption
Les atomes peuvent non seulement émettre de la lumière mais également en absorber. On peut constater ceci en faisant passer de la lumière blanche à travers un gaz froid avant de la disperser par un prisme.
Lorsqu'un gaz à basse pression et à basse température est traversé par de la lumière blanche, le spectre de la lumière transmise est constitué de raies noires se détachant sur le fond coloré du spectre de la lumière blanche : c'est un spectre de raies d'absorption. La propriété importante de ce spectre de raies d'absorption est que ses raies se produisent au même endroit que les raies d'émission : le gaz absorbe les radiations qu'il serait capable d'émettre s'il était chaud.
Les lois de Kirchoff
Les conditions de formation des différents spectres sont regroupées sous forme de lois, que l'on appelle les lois de Kirchoff.
- Un gaz, un solide ou un liquide à pression élevée, s'ils sont chauffés, émettent un rayonnement continu qui contient toutes les couleurs.
- Un gaz chaud, à basse pression, émet un rayonnement uniquement pour certaines couleurs bien spécifiques : le spectre de ce gaz présente des raies d'émission.
- Un gaz froid, à basse pression, situé après une source de rayonnement continu, en absorbe certaines couleurs, produisant ainsi dans le spectre des raies d'absorption.

Présence de raies sombres dans le spectre du Soleil. Kirchoff mesura la position de plusieurs milliers de raies du spectre solaire et montra qu'elles coïncidaient avec celles émises par divers éléments chimiques.
Crédit :
ASM
Applications
Ces lois sont fondamentales pour la spectroscopie et nous permettent ainsi de comprendre les spectres des astres. En effet, le Soleil et les étoiles émettent un spectre continu : on en déduit alors que les étoiles sont formées d'un gaz sous pression, à température élevée. Ils rayonnent comme les corps noirs.
Le spectre du Soleil présente des raies d'absorption, qui caractérisent les éléments chimiques constituant son atmosphère. En effet sa température varie de plusieurs millions de degrés, au centre, à quelques 5800 K en surface. Ainsi le rayonnement continu émis par le gaz chaud subit une absorption par le gaz qui constitue son atmosphère et qui est plus froid. On a ainsi accès la composition de son atmosphère car l'absorption est sélective, elle est caractéristique des éléments chimiques contenus dans celle-ci. On peut en conclure que l'atmosphère du Soleil est constituée d'un gaz sous basse pression.
Dans une grande variété de corps célestes, telles les comètes et certaines étoiles, on peut également observer des spectres d'émission. On en déduit que ces objets sont composés de gaz chaud à basse pression.
Crédit :
ASM
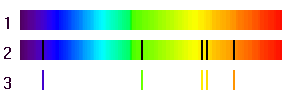
 Spectre d'une lampe à vapeur de sodium
Spectre d'une lampe à vapeur de sodium
Difficulté : ☆
Temps : 5 min
Le spectre de la lumière émise par une lampe à vapeur de sodium présente deux raies très rapprochées. On les appelle doublet du sodium. Elles ont pour longueur d'onde 589,0 nm et 589,6 nm.
Question 1)
Quelle est la couleur de la lumière émise par cette lampe ?
Les limites en longueurs d'onde des couleurs du spectre d'une lumière blanche sont les suivantes, en nm:
Violet : 400-424 ; Bleu : 424-491 ; Vert : 491-575 ; Jaune:575-585 ; Orange : 585-647 ; Rouge : 647-700.
Aller prendre l'air le soir en ville, dans un coin avec éclairage public.
Question 2)
Comment peut-on réaliser le spectre d'émission de cette vapeur et le spectre d'absorption de cette vapeur ?
Pour le spectre d'émission... recommencer la balade de nuit.
Question 3)
Décrire l'aspect de ces deux spectres
Demander aux spectres et autres fantômes rencontrés durant vos précédentes balades nocturnes.
Présentation du modèle de Bohr
Dans le modèle de Bohr semi-classique, l'électron tourne autour du noyau dans une orbite circulaire, comme une planète autour du Soleil. Un électron en orbite autour du noyau devrait rayonner et, perdant son énergie par rayonnement, tomber sur le noyau. Or ceci ne se produit pas, puisque les atomes sont stables. Bohr supposa alors qu'il existe certaines orbites où l'électron n'émet pas de rayonnement. Ceci arrive chaque fois que le moment de la quantité de mouvement de l'électron est un multiple entier de h/2π (où h est la constante de Planck 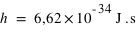 ): on numérote par 1, 2, ...., n les orbites successives ainsi permises.
): on numérote par 1, 2, ...., n les orbites successives ainsi permises.
Application à l'atome d'hydrogène
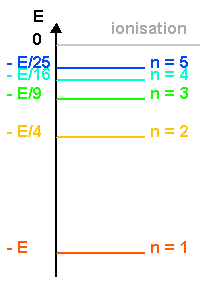
Considérons l'atome d'hydrogène. Son électron ne peut se trouver que sur l'une de ces orbites. Chaque orbite correspond à un niveau d'énergie donné de l'atome: le niveau d'énergie le plus bas, dit niveau fondamental, correspond à l'orbite la plus proche du noyau, qui porte le numéro n=1. Plus n est grand et plus l'orbite a un grand rayon, ce qui veut dire que l'énergie de l'atome est plus élevée. La valeur de n infinie correspond à une orbite de rayon infini, c'est-à-dire à l'ionisation de l'atome. L'énergie correspondante est de 13,6eV.
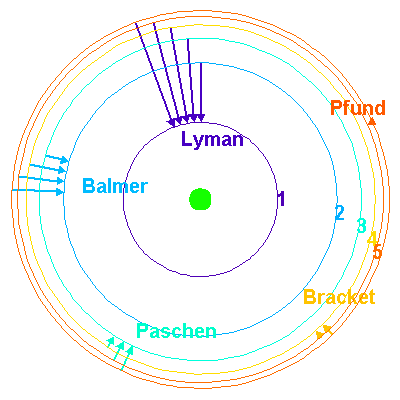
Représentation des niveaux d'énergie dans le modèle de Bohr : le noyau est symbolisé en vert au centre ; l'électron ne peut occuper qu'un nombre quantifié d'orbites.
Crédit :
ASM
L'atome d'hydrogène ne peut absorbe ou émettre qu'un photon d'énergie bien définie.
Lorsque l'électron retombe d'un niveau excité dans un niveau de plus basse énergie, il y a émission d'un rayonnement qui transporte exactement l'énergie correspondant à la différence d'énergie entre les deux niveaux.
Pour qu'il y ait émission il faut que l'énergie du niveau initial soit supérieur à l'énergie du niveau final c'est-à-dire que En > Em, n étant le niveau initial et m le niveau final. Or la mécanique quantique montre que pour l'atome d'hydrogène, l'énergie des différents niveaux est définie par l'expression :
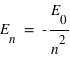
où n est un entier (il s'agit des différents niveaux), et E0 l'énergie nécessaire pour ioniser l'atome d'hydrogène à partir de son niveau fondamental, (valeur est égale à 13,6 eV).
Le photon ainsi émis a une énergie égale à la différence d'énergie entre les deux orbites soit Em-En. Cette énergie correspond, par l'équation de Planck (E=hν), à une onde électromagnétique de fréquence ν bien définie. Le saut d'énergie se manifeste donc par une raie d'émission dans le spectre de l'atome. On en déduit alors :
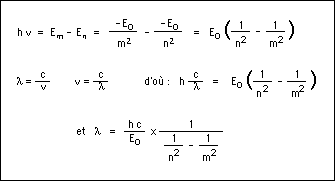
ou encore
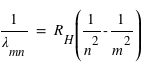
avec la constante de Rydberg :
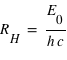
L'atome d'hydrogène peut aussi absorber de l'énergie, ceci lui permettant de passer d'un niveau inférieur à un niveau supérieur, par exemple en absorbant un photon. Mais ceci n'est possible que si le photon possède exactement l'énergie nécessaire, c'est-à-dire la différence d'énergie entre le niveau d'arrivée et le niveau de départ.
 Niveaux d'énergie de l'atome d'hydrogène
Niveaux d'énergie de l'atome d'hydrogène
Difficulté : ☆
Temps : 10 minutes
Question 1)
Calculer les énergies (en eV) des quatre premiers niveaux de l'atome d'hydrogène et donner le diagramme des niveaux d'énergie.
Il suffit d'utiliser la relation :
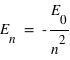
où E0=13,6 eV
 Constante de Rydberg
Constante de Rydberg
Difficulté : ☆☆
Temps : 15 minutes
Question 1)
Connaissant l'énergie d'ionisation E0=13,6eV, calculer la valeur de RH dans l'expression :
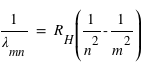
 Lampe à vapeur de mercure
Lampe à vapeur de mercure
Difficulté : ☆
Temps : 5 min
Dans la lumière d'une lampe à vapeur de mercure on trouve les trois radiations monochromatiques caractérisées par leur longueur d'onde λ1=578 nm ; λ2=546 nm; λ3=436 nm
Question 1)
A quel domaine spectral appartiennent-elles ?
Question 2)
Calculer la fréquence de ces trois radiations.
Les raies de Balmer
Les premières raies spectrales de l'hydrogène qui furent étudiées sont situées dans le domaine visible du spectre, bien qu'elles aillent en se resserrant vers une limite située dans le proche ultraviolet. Cette série de raies s'appelle la série de Balmer. Les premières raies sont numérotées au moyen de l'alphabet grec. La première raie, Hα a une longueur d'onde 656,2 nm, elle est donc rouge; la seconde, Hβ, est bleue à 486,1 nm, la troisième, Hγ, est violette à 434,0 nm, et ainsi de suite, jusqu'à 364,6 nm. Cette dernière est la longueur d'onde limite de la série de Balmer.
Raies de Balmer

Les raies de Balmer observées en laboratoire.
Crédit :
tbd
 Objectifs
Objectifs
L'hydrogène, constituant majoritaire, présente des signatures spectrales bien précises.
Le cas de l'hydrogène
L'atome le plus simple est celui de l'hydrogène, et c'est également celui qui possède le spectre le plus simple. On va décrire le spectre de cet élément, qui est par ailleurs l'élément le plus répandu dans l'univers.
Raies de l'hydrogène
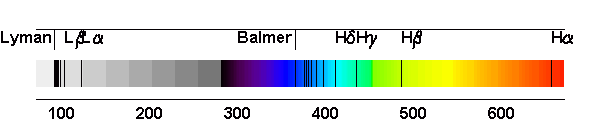
Spectre de raies de l'atome d'hydrogène.
Crédit :
ASM
Les séries de Balmer, Paschen...
Les premières raies spectrales de l'hydrogène qui furent étudiées sont situées dans le domaine visible du spectre, bien qu'elles aillent en se resserrant vers une limite située dans le proche ultraviolet. Cette série de raies s'appelle la série de Balmer. Les premières raies sont numérotées au moyen de l'alphabet grec. La première raie, Hα a une longueur d'onde 656,2 nm, elle est donc rouge; la seconde, Hβ, est bleue à 486,1 nm, la troisième, Hγ, est violette à 434,0 nm, et ainsi de suite, jusqu'à 364,6 nm. Cette dernière est la longueur d'onde limite de la série de Balmer.
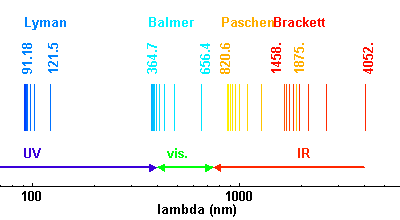
Quand le niveau inférieur est le niveau fondamental, la série de raies porte le nom de série de Lyman. Cette série de raies est située dans l'ultraviolet. La série de raies correspondant à un niveau inférieur de rang n=2 est située dans le visible et porte le nom de série de Balmer. La série de raies correspondant à un niveau inférieur de rang n=3 est située dans l'infrarouge : on l'appelle la série de Paschen.
Raies de l'hydrogène

Familles spectrales de l'hydrogène, définies par le niveau d'énergie inférieur.
Crédit :
ASM
 Calcul de longueurs d'ondes
Calcul de longueurs d'ondes
Difficulté : ☆
Temps : 15 minutes
Question 1)
Calculer la longueur d'onde des premières et dernières raies de Lyman, Balmer et Paschen de l'hydrogène et indiquer dans quel domaine du spectre électromagnétique ces ondes se situent.
L'expression suivante vous sera utile :
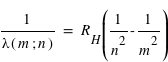
où n est l'état final c'est-à-dire 1 pour les raies de Lyman, 2 pour les raies de Balmer et 3 pour les raies de Paschen; m étant l'état initial (pour Lyman la première raie m = 2 et la dernière raie m = ∞).
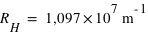





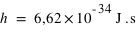 ): on numérote par 1, 2, ...., n les orbites successives ainsi permises.
): on numérote par 1, 2, ...., n les orbites successives ainsi permises.

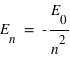
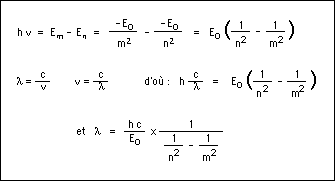
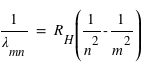
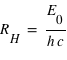
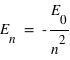
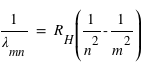


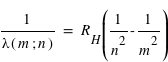
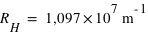
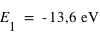 .
.
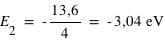
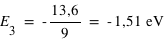
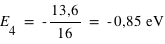
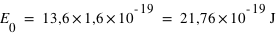 .
On en déduit alors la valeur :
.
On en déduit alors la valeur :