
|
Même s'il reprend les bases théoriques, ce cours suppose que le réseau a déjà été étudié en physique. Un réseau est alimenté en faisceau parallèle par une fente source, et en donne une série d'images colorées.
Caractériser les interférences constructives d'un réseau ; voir la distribution de l'énergie dans la figure d'interférence.
On note 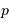 la période du réseau,
la période du réseau, 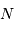 le nombre de traits,
le nombre de traits, 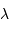 la longueur d'onde étudiée.
La condition d'interférences constructives s'écrit :
la longueur d'onde étudiée.
La condition d'interférences constructives s'écrit :
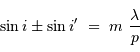
avec 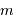 , entier, l'ordre d'interférence. Le signe
, entier, l'ordre d'interférence. Le signe 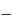 dans cette relation concerne un réseau par transmission, le signe
dans cette relation concerne un réseau par transmission, le signe  un réseau par réflexion. C'est ce dernier cas qui nous intéresse, car il correspond au cas du réseau blazé.
un réseau par réflexion. C'est ce dernier cas qui nous intéresse, car il correspond au cas du réseau blazé.
Cette condition rend compte
que le déphasage 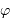 entre les amplitudes complexes issues de 2 traits consécutifs, vaut
entre les amplitudes complexes issues de 2 traits consécutifs, vaut 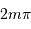 (ou bien, de façon équivalente, que la différence de marche vaut
(ou bien, de façon équivalente, que la différence de marche vaut 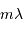 ).
).
La diffraction par une fente du réseau détermine les différentes directions vers lesquelles la lumière est envoyée, chacun des fentes du réseau se comportant comme une source secondaire.
Les interférences entre ces différentes sources secondaires construisent les franges d'interférences, d'autant plus fines que le réseau comporte un nombre important de traits (cf. calcul de l'intensité de la figure d'interférence).
L'intensité de la figure d'interférence est issue du double effet de la
diffraction par une seule fente et des interférences par 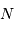 fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note
fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note 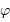 le déphasage entre 2 fentes consécutives, et
le déphasage entre 2 fentes consécutives, et 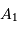 l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
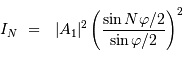
La sommation des amplitudes conduit à :
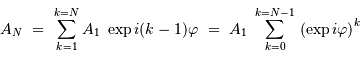
Le traitement de la somme des termes d'une suite en progression géométrique donne :
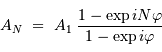
On calcule l'intensité en factorisant le numérateur et le dénominateur par l'exponentielle complexe de l'angle moitié (de module unité), pour aboutir à :
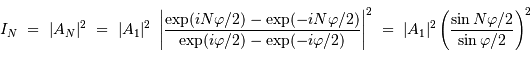
Le terme d'intensité est important uniquement lorsque le dénominateur s'annule. Dans ce cas, le numérateur s'annule également et, par continuité du rapport,
le pic d'intensité tend vers 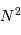 . Chaque pic correspond à un ordre d'interférence. La largeur de ce pic est donnée par les variations du numérateur, qui oscille
. Chaque pic correspond à un ordre d'interférence. La largeur de ce pic est donnée par les variations du numérateur, qui oscille 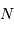 fois plus rapidement que le dénominateur ; elle est donc
fois plus rapidement que le dénominateur ; elle est donc 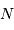 fois inférieure à la largeur entre 2 ordres consécutifs.
fois inférieure à la largeur entre 2 ordres consécutifs.
L'inconvénient du réseau par transmission ici décrit est qu'il n'est a priori pas efficace : l'essentiel de l'énergie passe dans l'ordre 0, inintéressant pour la dispersion. Un concept technologique spécifique pare cet inconvénient : le réseau blazé.