La révolution des satellites de Jupiter
Auteur: Françoise Roques / Florence Henry
- Introduction
- Documents
- Déroulement
- Introduction
- Stratégie
- Utilisation du programme Jupiter
- Procédure - 1
- Procédure - 2
- Procédure - 3
- Questions et discussion
- Données astronomiques
Introduction
Champ: Système Solaire
Temps: 2 à 3 heures, selon le niveau des élèves
Niveau: **
 Prérequis
Prérequis
Savoir utiliser la règle de 3
 Objectifs
Objectifs
Vous devrez être capable de déterminer la masse de Jupiter en mesurant les propriétés des orbites des satellites de Jupiter et en les analysant à l'aide de la troisième loi de Kepler.
Si vous apprenez à :
- Interpréter un mouvement d'aller et retour comme la projection d'un mouvement circulaire et d'utiliser cette interprétation pour mesurer les orbites des satellites
- Découvrir la relation entre le rayon d'une orbite et la période pour un système lié par la gravitation
- Porter ces résultats sur un graphique et y ajuster une courbe sinusoïdale
Vous pourrez :
- Appliquer la loi gouvernant ce mouvement (troisième loi de Kepler) pour calculer la masse de Jupiter
- Estimer la période orbitale ou le rayon pour une autre lune de Jupiter.
Documents
Déroulement
Introduction
Nous allons observer les quatre lunes de Jupiter, vues au travers d'un télescope. Elles furent nommées Io, Europe, Ganymède et Callisto, par ordre de leur distance à Jupiter. Si vous regardez avec un petit télescope, vous verrez ceci
Crédit :
CLEA/Gettysburg College
Les lunes apparaissent alignées parce que le plan orbital des satellites est vu par la tranche. Avec le temps, les lunes bougent par rapport à Jupiter. Les lunes suivent une orbite à peu près circulaire mais on ne voit, de la Terre, que la projection du mouvement dans le plan du ciel. On ne peut pas connaître la distance de la lune à Jupiter mais seulement la distance apparente (cf. figure 1), autrement dit, la distance de la lune à la droite joignant Jupiter à la Terre (ligne de visée).
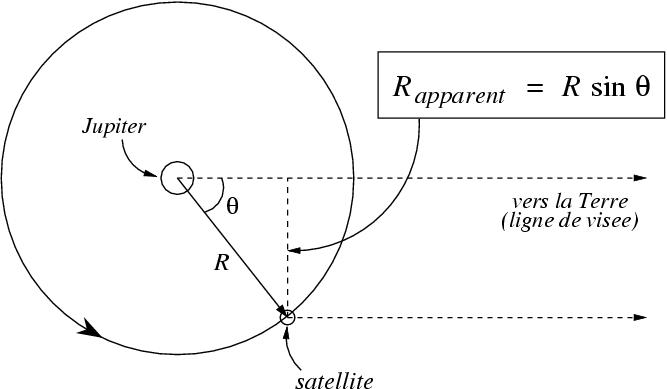
Figure 1 : Géométrie de la troisième loi de Kepler
Crédit :
CLEA/Gettysburg College
La distance de la lune à la ligne de visée en fonction du temps est une courbe sinusoïdale (cf. figure 2). En prenant assez de mesures de la position apparente de la lune, on peut ajuster une sinusoïde aux points de données et déterminer le rayon de l'orbite (l'amplitude de la courbe) et la période de l'orbite (la période de la sinusoïde). Quand vous connaissez le rayon et la période de l'orbite de cette lune, et que vous l'avez converti dans les bonnes unités, vous pouvez déterminer la masse de Jupiter en utilisant la troisième loi de Kepler. Vous déterminerez la masse de Jupiter pour chacune des quatre lunes. Les erreurs associées à chaque lune feront que les résultats seront différents d'une lune à l'autre.
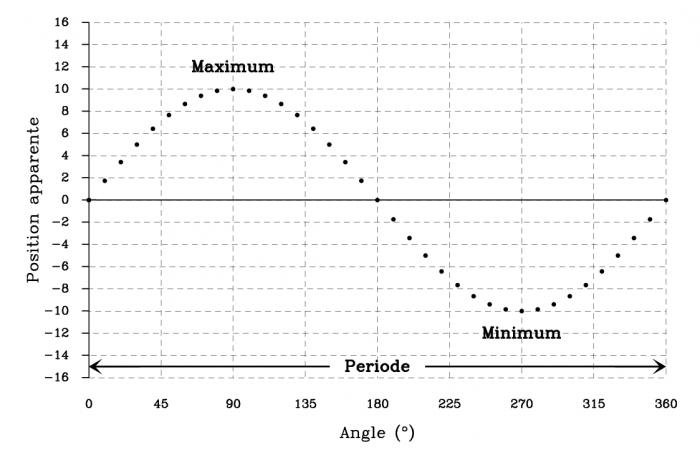
Figure 2 : Position apparente d'une lune
Crédit :
CLEA/Gettysburg College
Le programme Jupiter simule l'utilisation d'un télescope contrôlé automatiquement et équipé d'une caméra CCD qui fournit une image vidéo sur l'écran de l'ordinateur. Le programme qui permet de faire ces mesures et d'ajuster le taux d'agrandissement de l'image du télescope est complexe mais il simule de façon réaliste cette expérience et vous permet de comprendre comment les astronomes collectent leurs données et contrôlent le télescope. Au lieu d'utiliser un télescope et d'observer les lunes de Jupiter pendant plusieurs jours, ce programme simule l'aspect des lunes telles que vous les verriez au télescope avec l'intervalle de temps que vous fixerez.
Stratégie
Les différentes actions à entreprendre dans cet exercice sont :
- Utiliser le programme Jupiter pour observer et mesurer la position apparente des lunes de Jupiter. La lune à observer vous sera indiquée, ainsi que la date de départ et l'intervalle entre deux observations et le nombre total de jours. Notez que des observations différentes peuvent être demandées à des groupes différents.
- Portez vos observations pour chaque lune, sur les feuilles quadrillées fournies dans le fichier feuilles.pdf, ou reproduisez ces figures sur du papier millimétré.
- Dessinez soigneusement la courbe (sinusoïde) correspondant le mieux aux données du graphe.
- Déterminer la période et le demi grand axe de l'orbite de chaque lune et convertissez ces valeurs respectivement en années et Unités Astronomiques.
- Calculez la masse de Jupiter à partir des observations de chaque lune, et déterminez la valeur moyenne.
Utilisation du programme Jupiter
- 1. Ouvrez le programme Jupiter en double-cliquant dessus avec la souris
- 2. À tout moment, vous pouvez sélectionner « Help » pour avoir de l'aide en ligne (en anglais). Il y a quatre choix dans le menu « help » :
- « Getting started » (Préparation) vous explique comment régler le programme avant de commencer à saisir les données
- « Taking data » (saisir les données) explique comment manipuler le programme pour saisir les données
- « User » (Utilisateur), inactif pour ce programme
- et « About this exercice » (à propos de cet exercice) donne le titre et le numéro de version du programme et des informations de copyright.
Vous pouvez quitter la fenêtre « Help » en sélectionnant « Close » dans le coin supérieur gauche de la fenêtre. Vous pouvez laisser la fenêtre « Help » ouverte en travaillant en changeant sa taille. - 3. Vous devez d'abord sélectionner « Log In » dans le menu avant de saisir les données. Vous pouvez alors entrer les noms de chaque élève du groupe ainsi que le numéro de la table. N'utilisez pas de ponctuation. Appuyez sur retour après chaque nom ou placez le curseur sur la case suivante avec la souris. Quand toutes les informations sont entrées, validez avec OK pour continuer.
- 4. Choisissez « Start » pour commencer le programme. Une boîte de dialogue apparaît et demande la date et l'heure de début. Entrez les valeurs souhaitées. Les valeurs par défaut sont la date courante. L'intervalle de temps entre deux observations peut aussi être changé. Pour revenir aux informations précédentes, cliquez sur « cancel ». quand toutes informations sont correctes, cliquez « OK ».
- 5. Il y a quatre taux d'agrandissement possibles que vous choisissez en cliquant sur les boutons 100X, 200X, 300X, 400X, en bas de l'écran. Pour améliorer la précision de vos mesures, choisissez la plus grande fenêtre possible qui permet de voir la lune sur l'écran.
- 6. Pour mesurer la distance projetée de la lune à Jupiter, déplacez le curseur pour que la pointe de la flèche (ou la croix selon les versions) soit sur la lune et cliquez sur la souris. Les informations sur la lune apparaîtront à l'écran. Il s'agit du nom de la lune, de ses coordonnées, x et y en pixels et de la distance projetée à Jupiter (l'unité est le diamètre de Jupiter). La lettre W ou E signifie respectivement que la lune se trouve à l Ouest ou à l Est de la planète. Si aucun nom n'apparaît, cela signifie que vous avez mal centré la lune ; recommencez votre mesure.
- 7. Quand vous avez enregistré le Temps Universel et la distance pour toutes les lunes, vous pouvez passer aux observations suivantes en cliquant sur « Next ».
- 8. Quand vous avez terminé de lire les données, vous terminez le programme en cliquant sur « Quit ».
Procédure - 1
Lancez le programme et entrez vos noms en sélectionnant « Log in ». Chaque groupe d'élèves réalisera et enregistrera une session différente d'observations. Les dates de début d'observations de chaque groupe seront écrites au tableau. Notez sur la feuille de données les rendeignements vous concernant (groupe, année, mois, jour, nombre d'observations et intervalle entre chaque) puis sélectionner « Start » et entrez ces données dans le programme comme montré en section 4 de Utilisation du programme Jupiter.
Après avoir cliqué sur « OK », vous verrez apparaître la figure 3.
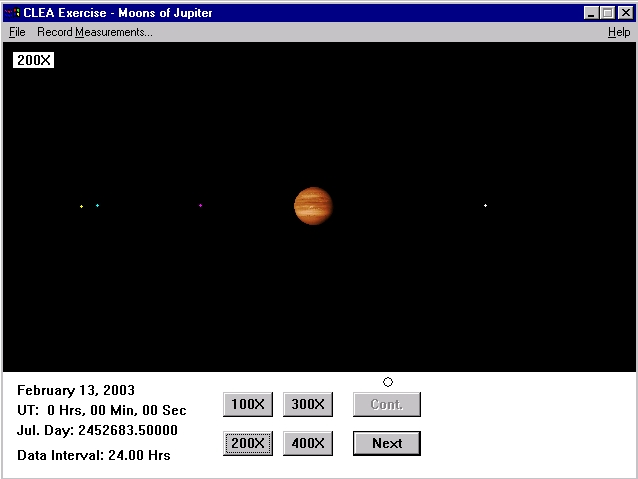
Figure 3 : Photo d'écran du logiciel en action
Crédit :
CLEA/Gettysburg College
Jupiter est au centre de l'écran et les points de part et d'autres sont les lunes. Il arrive qu'une lune soit derrière Jupiter et ne soit donc pas visible. Même avec un très fort grossissement, elles sont beaucoup plus petites que Jupiter. Le grossissement effectif est affiché dans le coin gauche de l'écran. La date, le UT (Temps Universel) et J.D. (Diamètre de Jupiter) sont aussi donnés à l'écran.
Cliquez sur chaque lune pour connaître à quelle distance du centre de Jupiter se trouve la lune (l'unité est le diamètre de Jupiter). Vous pouvez vérifier que le bord de Jupiter est à 0.5 J.D. Pour mesurer précisément la position de chaque lune, choisissez l'agrandissement optimal qui laisse la lune sur l'écran. Si une lune est derrière Jupiter, notez 0 pour la distance de cette lune. Le tableau suivant montre un exemple d'enregistrement de données.
Exemple d'enregistrement
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
| date |
heure |
jour |
Io |
Europe |
Ganymède |
Callisto |
| 24/07 |
0.0 |
1.0 |
+2.95 |
+2.75 |
-7.43 |
+13.15 |
| 24/07 |
12.0 |
1.5 |
-0.86 |
+4.7 |
-6.3 |
+13.15 |
- (1) : Date
- (2) : Temps Universel
- (3) : Numéro du jour (1, 2, 3...)
- (4) - (7) : Positions de chaque lune sous son nom. Utilisez + pour Ouest et - pour l'Est. Si le programme donne comme position pour Europe x=2.75W, vous entrerez +2.75 dans la colonne (5)
Procédure - 2
Enregistrez vos 18 lignes de données sur la feuille prévue à cet effet (1ère page de feuilles.pdf), en suivant le modèle du tableau précédent. Pour les positions, utilisez + pour Ouest et - pour l'Est. Si le programme donne comme position pour Europe x=2.75W, vous entrerez +2.75 dans la colonne (5).
Vous devez maintenant analyser les données. En portant les positions en fonction du temps, vos données vous permettront d'obtenir un graphe semblable au graphe de la figure 4 (ce dessin concerne une lune imaginaire appelée CLEA).
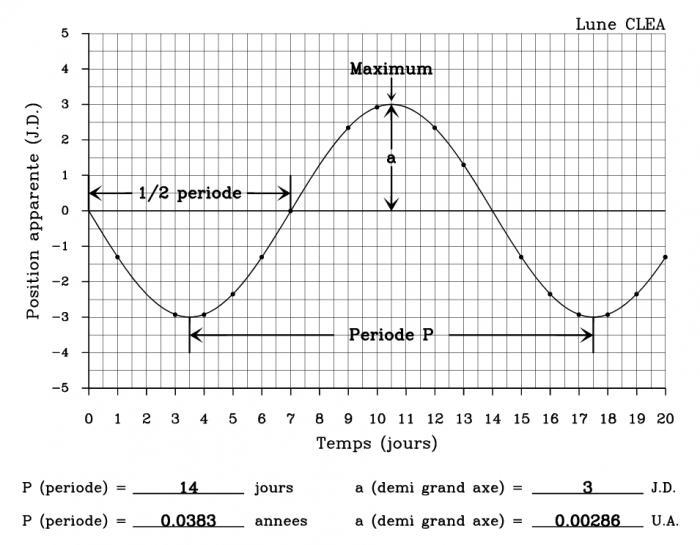
Figure 4 : Graphique pour une lune imaginaire
Crédit :
CLEA/Gettysburg College
Chaque point de la figure est une observation de la lune CLEA. Notez l'espacement irrégulier des points, dû au mauvais temps ou à un autre problème d'observation durant certaines nuits. La courbe continue joignant les points est ce que vous observeriez en réduisant assez l'intervalle de temps entre les observations. La forme de la courbe est une sinusoïde. Vous devez déterminer la sinusoïde qui s'ajuste le mieux à vos données pour déterminer les propriétés orbitales de chaque lune. Il faut se rappeler que :
- Les orbites des satellites sont régulières, c'est-à-dire qu'ils n'accélèrent ni ne ralentissent pas d'une période à l'autre.
- Le rayon des orbites ne change pas d'une période à l'autre.
La sinusoïde que vous dessinez doit donc être régulière. Elle doit passer par tous les points. Les valeurs des maxima doivent être constantes et la distance entre ces sommets doit être constante.
Les données de la lune CLEA permettent de déterminer le rayon et la période de l'orbite. La période est le temps mis pour aller d'un point à un point semblable sur la courbe. En particulier, le temps entre deux maxima est la période. Le temps entre deux croisements de l'axe horizontal (position =0) est la moitié de la période parce que c'est le temps que met le satellite pour aller de devant Jupiter à derrière Jupiter, (ou l'inverse).
Pour votre lune, il ne vous est pas nécessaire d'avoir des données couvrant une période entière ; Vous pouvez trouver la période en déterminant le temps entre deux points position =0. et le multipliant par deux. Vous pouvez aussi obtenir une meilleure détermination de la période en déterminant le temps mis par la lune pour effectuer par exemple 4 périodes, puis en divisant ce temps par 4. Quand une lune est dans une position extrême à l'est ou à l'ouest, la distance apparente est maximale. Rappelez-vous que les orbites sont presque circulaires, mais que, vues de côté, on ne peut trouver le rayon de l'orbite que quand le satellite est dans une position extrême d'un côté ou de l'autre.
Procédure - 3
Reportez les données de chaque lune sur les graphiques des pages 2, 3, 4 et 5 de feuilles.pdf. Sur l'axe horizontal, portez les numéros des jours de vos observations. L'échelle verticale est déjà donnée. Chaque mesure de la distance apparente de la lune à Jupiter vous donne un point à porter sur le graphique. Il faut s'assurer qu'un point correspond bien à une session d'observation.
Pour chaque lune, dessiner une courbe passant par les points. Marquez les maxima et les minima par des croix. Ils ne tombent pas forcément sur une ligne verticale de la grille. La courbe doit être symétrique par rapport à l'axe horizontal, c'est-à-dire que les maxima et les minima doivent avoir les mêmes valeurs, au signe près.
 Remarque
Remarque
Commencez par les lunes extérieures (Ganymède et Callisto), puis faîtes les lunes intérieures (Io et Europe).
Estimez la valeur de la période, 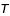 , et du rayon orbital,
, et du rayon orbital, 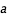 , sur les graphes, avec la méthode expliquée pour la lune CLEA (cf. figure 4).
, sur les graphes, avec la méthode expliquée pour la lune CLEA (cf. figure 4).
 Remarque
Remarque
Si vouz avez trop de mal à déterminer les périodes d'Io et d'Europe, vous pouvez recommencer la prise de données en faisant une observation toutes les 12 heures.
Les unités de ces valeurs sont le jour pour 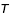 et J.D. pour
et J.D. pour 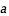 . Pour pouvoir utiliser la troisième loi de Kepler, vous devez changer d'unités :
. Pour pouvoir utiliser la troisième loi de Kepler, vous devez changer d'unités :
- Pour obtenir la période en années, vous divisez en la divisant par le nombre de jours dans l'année (365).
- Pour obtenir le rayon orbital en U.A., vous devez le diviser par le nombre de diamètres de Jupiter dans une U.A. (1050).
Écrivez ces valeurs sous chaque graphique. Vous avez maintenant toutes les informations pour appliquer la troisième loi de Kepler et calculer la masse de Jupiter : 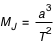 Où
Où 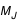 est la masse de Jupiter en masse solaire,
est la masse de Jupiter en masse solaire, 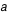 est le rayon de l'orbite en U.A. et
est le rayon de l'orbite en U.A. et 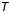 est la période de l'orbite en années terrestres.
est la période de l'orbite en années terrestres.
Calculer la masse de Jupiter pour chaque cas. Si une valeur est très différente des autres, recherchez une source d'erreur. S'il n'y a pas d'erreur, c'est que les données ne permettent pas une meilleure estimation. Gardez alors la valeur que vous avez obtenue.
Reportez toutes les valeurs calculées dans sur la feuille de TP.
Questions et discussion
- 1. Exprimez la masse de Jupiter en masses terrestres en divisant par 3,00 10-6, (la masse de la Terre en masses solaire).
- 2. Autour de Jupiter, il y a des satellites au delà de Callisto. Auront-ils des périodes plus grandes ou plus petites que celle de Callisto? Pourquoi ?
Questions supplémentaires :
- 1. Qu'est-ce qui, à votre avis, sera une plus grande source d'erreur : une erreur de 10 pour cent sur
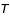 ou une erreur de 10 pour cent sur
ou une erreur de 10 pour cent sur 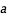 ? Pourquoi ?
? Pourquoi ? - 2. L'orbite de la Lune a une période de 27,3 jours et un rayon (appelé demi grand axe parce que l'orbite est excentrique) de 2,56 10-3
U.A. (soit 3,84 105
km). Quelle est la masse de la terre ? Dans quelle unité ?
Données astronomiques
Voici quelques données (distances, périodes de rotation et masses) qui pourront vous servir pour vérifier vos résultats ou pour comparer les ordres de grandeur du système Terre-Lune avec le système Jovien.
Quelques distances ...
| Distance moyenne Terre - Lune |
384 000 km |
| Distance moyenne Jupiter - Io |
422 000 km |
| Distance moyenne Jupiter - Europe |
671 000 km |
| Distance moyenne Jupiter - Ganymède |
1 070 000 km |
| Distance moyenne Jupiter - Callisto |
1 883 000 km |
... des périodes ...
| Période de la Lune |
27,32 jours |
| Période d'Io |
1,77 jours |
| Période d'Europe |
3,55 jours |
| Période de Ganymède |
7,15 jours |
| Période de Callisto |
16,69 jours |
... et des masses
| Masse de Jupiter |
1,900 1027 kg |
| Masse de la Terre |
5,972 1024 kg |
| Masse du Soleil |
1,989 1030 kg |
 Prérequis
Prérequis Objectifs
Objectifs Introduction
Introduction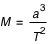 où
où
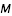 est la masse de la planète (comptée en masse solaire)
est la masse de la planète (comptée en masse solaire)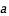 est le demi grand axe de l'orbite elliptique (compté en U.A., Unité Astronomique, qui est la distance moyenne du Soleil à la Terre)
est le demi grand axe de l'orbite elliptique (compté en U.A., Unité Astronomique, qui est la distance moyenne du Soleil à la Terre)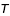 est la période (comptée en années terrestres). La période est le temps nécessaire au satellite pour faire un tour autour de la planète.
est la période (comptée en années terrestres). La période est le temps nécessaire au satellite pour faire un tour autour de la planète.




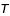 , et du rayon orbital,
, et du rayon orbital, 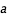 , sur les graphes, avec la méthode expliquée pour la lune CLEA (cf.
, sur les graphes, avec la méthode expliquée pour la lune CLEA (cf. 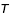 et J.D. pour
et J.D. pour 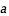 . Pour pouvoir utiliser la troisième loi de Kepler, vous devez changer d'unités :
. Pour pouvoir utiliser la troisième loi de Kepler, vous devez changer d'unités :
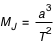 Où
Où 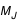 est la masse de Jupiter en masse solaire,
est la masse de Jupiter en masse solaire, 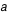 est le rayon de l'orbite en U.A. et
est le rayon de l'orbite en U.A. et 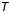 est la période de l'orbite en années terrestres.
est la période de l'orbite en années terrestres.
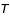 ou une erreur de 10 pour cent sur
ou une erreur de 10 pour cent sur 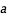 ? Pourquoi ?
? Pourquoi ?