Les signaux recherchés méritent, pour donner les meilleurs mesures possibles, des traitement appropriés. Cette section se propose d'étudier plus précisément quelques-unes des techniques de base de traitement du signal.
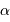 du Centaure.
du Centaure.
Les signaux recherchés méritent, pour donner les meilleurs mesures possibles, des traitement appropriés. Cette section se propose d'étudier plus précisément quelques-unes des techniques de base de traitement du signal.

 du Centaure.
du Centaure.
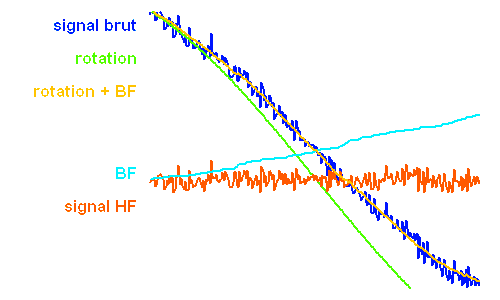
Dans la chaîne de traitement du signal, des observations brutes au résultat final, une étape souvent essentielle consiste à s'affranchir de signaux parasites. C'est possible lorsque ces derniers présentent des caractéristiques différentes de celles du signal, comme p.ex. un signal à basse fréquence qui contamine un signal sismique.
Un filtre par moyenne glissante substitue à une valeur donnée la moyenne des valeurs aux alentours, dans un intervalle de largeur 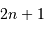 . Plus l'intervalle est grand, plus le filtrage est efficace.
. Plus l'intervalle est grand, plus le filtrage est efficace.
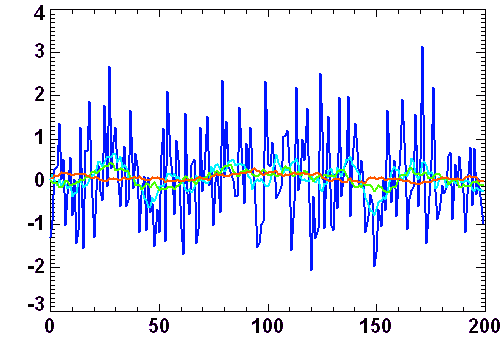
Ce filtrage présente des inconvénients que dévoile la transformée de Fourier.
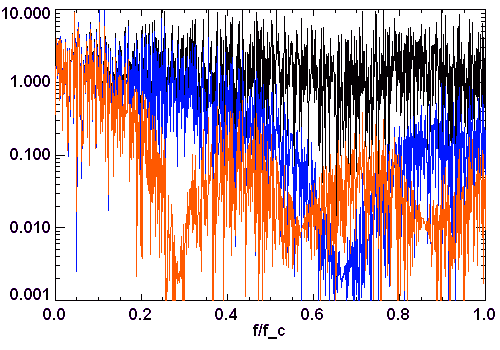
Un filtre par moyenne médiane substitue à une valeur donnée la médiane des valeurs aux alentours, dans un intervalle de largeur 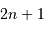 . Ce filtrage est efficace pour gommer les valeurs aberrantes.
. Ce filtrage est efficace pour gommer les valeurs aberrantes.
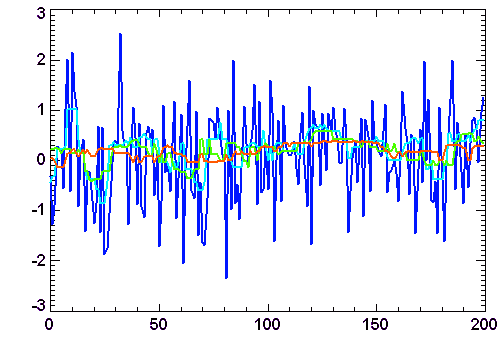
Réaliser une estimation linéaire d'une distribution de pont, c'est finalement ne décrire ce nuage de points que par 2 valeurs (ordonnée à l'origine et pente)
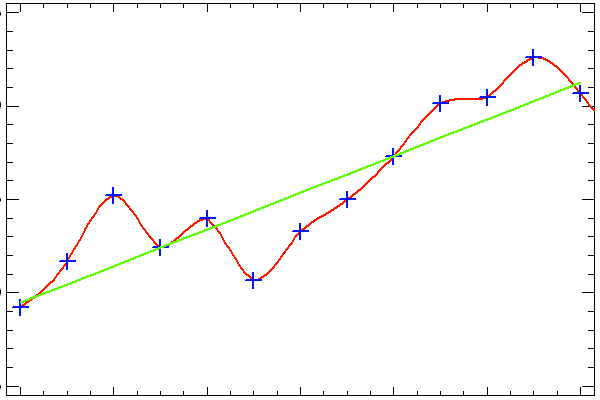
La correction de valeurs aberrantes est typiquement une opération de filtrage. Un filtrage par moyenne glissante ou par la médiane n'y parvient pas avec la même efficacité.
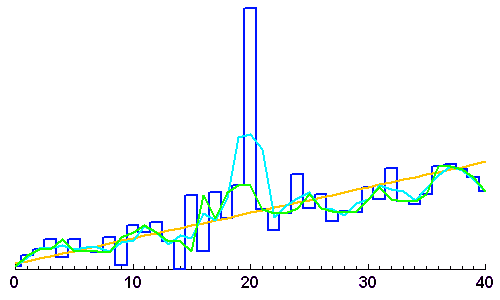
Toute série de données, dépendant de quelque paramètre que ce soit (temps, variable d'espace, autre variable), à n'importe quelle dimension, peut être décrite par ses composantes fréquentielles. Un filtrage ad hoc peut permettre de faire ressortir le signal des autres composantes.
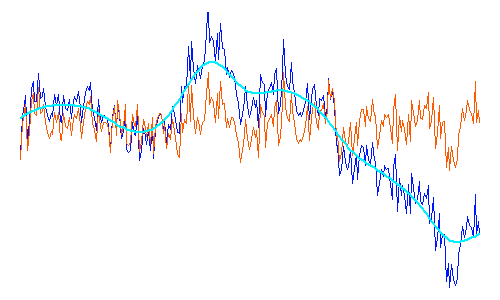
Analyse par transformée de Fourier
Aborder quelques-uns des (nombreux) aspects de la transformée de Fourier.
Il est souvent indispensable de séparer les différentes composantes en fréquences qui constituent une observation, pour extraire le signal de la contribution du bruit ou d'autres signaux, ce qui constitue un filtrage du signal. Le but n'est pas de présenter sous forme de cours les multiples filtres possibles, mais plutôt quelques-uns de leurs effets.
Toute acquisition de données, caractérisée par un pas de temps 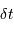 , filtre les fréquences temporelles plus rapides que
, filtre les fréquences temporelles plus rapides que 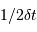 .
.
On peut reconsidérer la diffraction d'une onde plane monochromatique de longueur d'onde 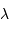 par une ouverture
par une ouverture  comme un filtrage des fréquences angulaires supérieures à
comme un filtrage des fréquences angulaires supérieures à 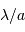 .
.
Les animations ci-jointes décortiquent le processus de filtrage par moyenne glissante ou par la médiane.
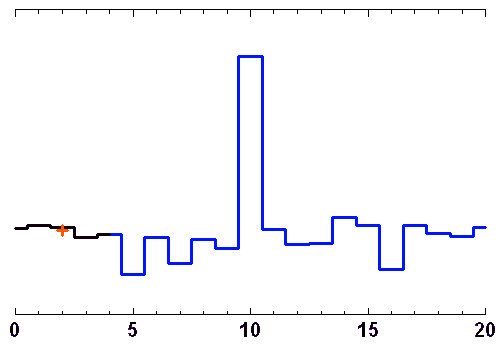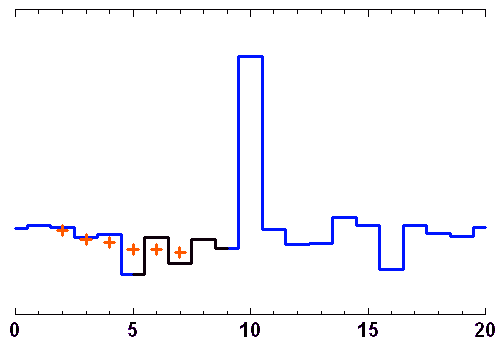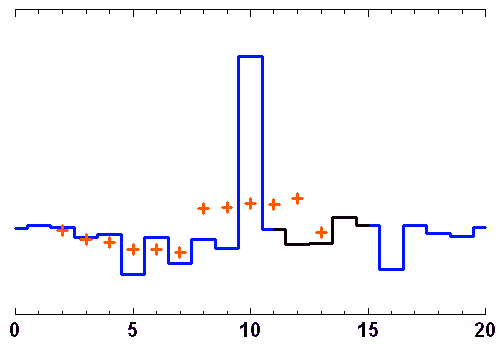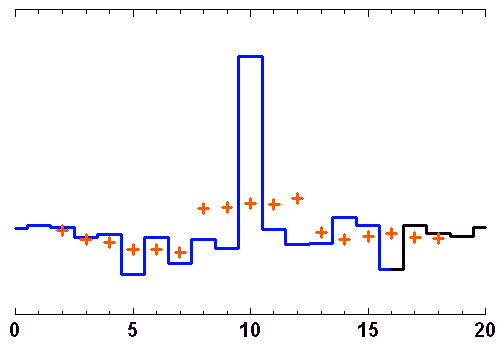
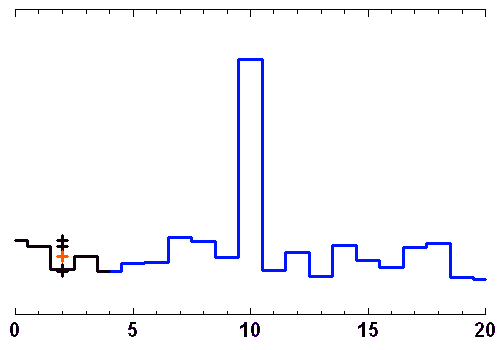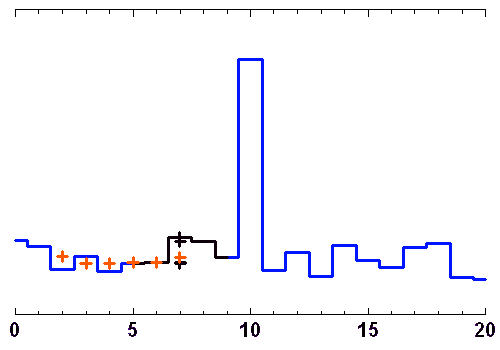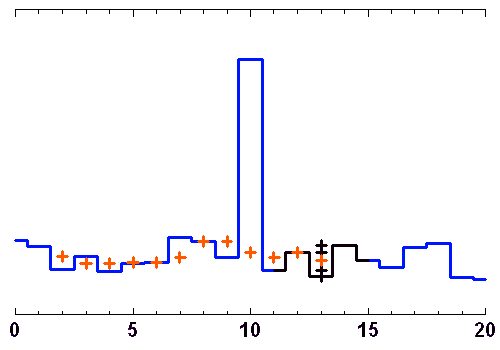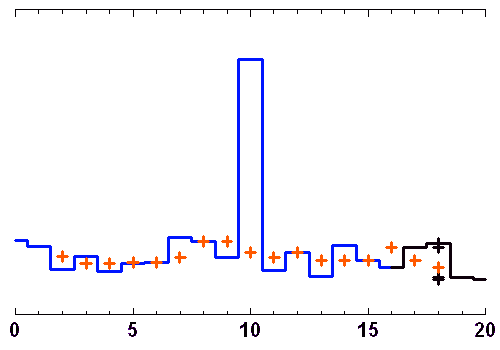

L'opération de filtrage n'est pas bégnine, et un filtre inadapté peut conduire à un mauvais résultat. Par exemple, le filtrage par moyenne glissante convient très mal pour un signal oscillant.
La série temporelle ci-jointe est filtrée par filtrage numérique (algorithme de filtre à trous), avec séparation des hautes et basses fréquence. Les domaines de fréquence sont définis par rapport à une fréquence de valeur arbitraire ou mûrement réfléchie...
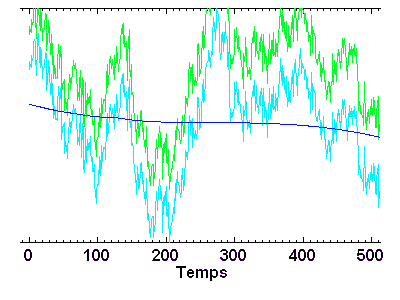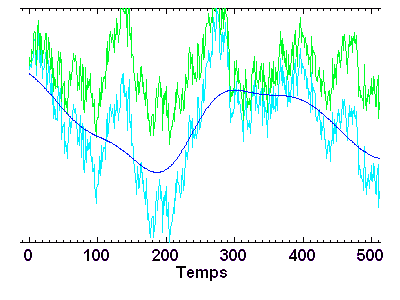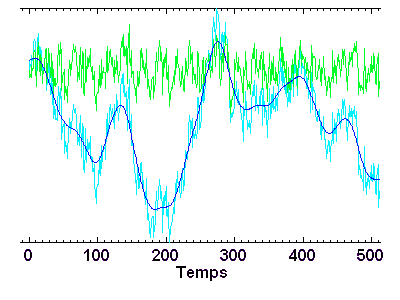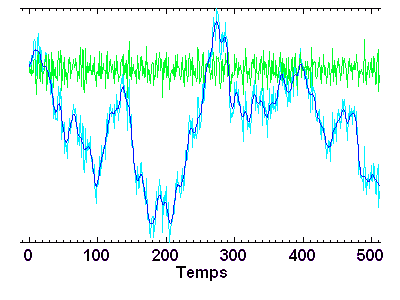
Les appliquettes ci-dessous dévoilent l'intérêt du filtrage. Elles représentent des cartes de Jupiter dans l'infrarouge thermique. Sans filtrage, c'est la structure en bandes parallèles à l'équateur qui domine l'image ; après filtrage de cette structure dominante, on voit apparaître des motifs de type ondulatoire, avec une dizaine de motifs répartis en longitude, couvrant une extension en latitude plus vaste que les bandes.
Utiliser les appliquettes pour dévoiler ces structures.


A l'aide de l'appliquette ci-jointe, on se propose d'illustrer l'évolution du bruit en sommant différentes images d'un même champ.
Correction du champ plat 
Approche mathématique de la transformation de Fourier
Présentation de la transformation de Fourier, et rappel de quelques propriétés.
La transformation de Fourier associe à une fonction 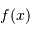 sa transformée~:
sa transformée~:
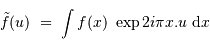
Les variables 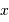 et
et 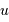 sont conjuguées. A la variable temporelle
sont conjuguées. A la variable temporelle 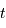 est associée la variable fréquentielle
est associée la variable fréquentielle 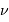 ; à la variable d'espace
; à la variable d'espace 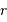 , la fréquence spatiale
, la fréquence spatiale 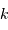 .
.
La TF est dotée de multiples propriétés (linéarité...) : se référer à un cours de maths.
L'opération inverse de la TF est notée :
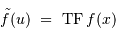 et
et
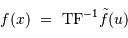 .
.
Il ne s'agit rien d'autre que de la conservation de l'énergie, qui ici s'exprime par :
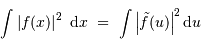
Autrement dit, l'énergie d'un signal ne peut pas dépendre de la description de ce signal, directe ou fréquentielle.
| grandeur | notation | unité | exemple |
|---|---|---|---|
| variable | 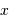 |
X | temps, en s |
| variable conjuguée | 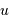 |
1/X | fréquence, en Hz |
| signal | 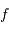 |
Y | vitesse, en m/s |
| spectre | 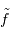 |
XY | m |
| spectre d'amplitude | 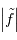 |
XY | m |
| spectre de puissance | 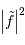 |
![[\mathrm{XY}]^2](../pages_traiter/equations_analyse-tf/equation18.png) |
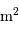 |
La définition de la transformation, continue, se doit d'être amendée pour tenir compte du fait qu'un signal réel est échantillonné. L'analyse de Fourier discrète s'appuie sur un nombre fini de réalisations du signal, et donne un nombre finie de fréquences pour le décrire. La discrétisation s'opère en douceur, car la TF d'une fonction peigne (succession équidistance de Dirac), fonction retranscrivant l'échantillonnage du signal, est une fonction peigne.
L'analyse de Fourier rapide (fast Fourier transform, ou FFT) est une une forme spécifique de programmation de la transformation de Fourier. Une routine de calcul fft est présente dans toute bonne bibliothèque de programmation.
L'usage d'une FFT implique:
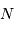 tel que
tel que 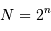 points, sinon le gain en temps est annulé, et la FFT peut
devenir
extrêmement lente si le nombre de points est premier, ou se
factorise avec de grands facteurs premiers.
points, sinon le gain en temps est annulé, et la FFT peut
devenir
extrêmement lente si le nombre de points est premier, ou se
factorise avec de grands facteurs premiers.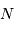 valeurs conduit à un spectre de
valeurs conduit à un spectre de 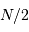 fréquences.
fréquences.L'appliquette ci-dessous permet de calculer et visualiser le spectre de puissance de certaines fonctions. La transformée de Fourier peut calculée soit directement, soit par FFT.

Avec comme signal une sinusoïde, comme méthode la fft, visualiser les effets :
Vérifier le lien entre la résolution en fréquence et la durée totale d'observation ; vérifier le lien entre le nombre de points et la fréquence de coupure.
Difficulté : ☆☆ Temps : 40 min
Vérifier l'homogénéité de la conservation de l'énergie énoncée par le théorème de Parseval-Plancherel.
Pour des raisons physiques, il est commode de poser la définition de la TF d'une série temporelle bornée sur un intervalle de temps 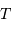 comme :
comme :
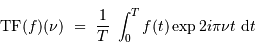
avec le changement de notation pour préciser la différence par rapport à la TF classique. Montrer l'intérêt physique de cette notation, en s'appuyant p.ex. sur un signal purement sinusoïdale.
Pour d'autre raisons, il peut être commode de poser la définition de la TF d'une série temporelle discrète d'une manière différente :
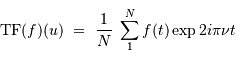
avec le changement de notation pour préciser la différence par rapport à la TF classique. Réécrire la relation de Parseval-Plancherel, et montrer que
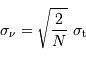
où 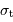 et
et 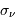 sont respectivement les écarts-types de la série temporelle et du spectre.
sont respectivement les écarts-types de la série temporelle et du spectre.
La TF permet la recherche de composantes périodiques dans un signal. Les signaux ci-contre sont équivalents. L'un correspond à une série temporelle, l'autre à son spectre de Fourier.
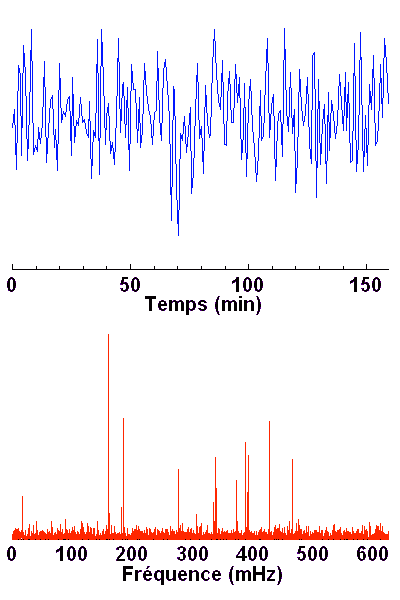
L'astérosismologie est un sujet en plein développement, dont les observations se basent sur de longues séries temporelles, pour l'identification des modes propres d'oscillations dans le spectre de Fourier.
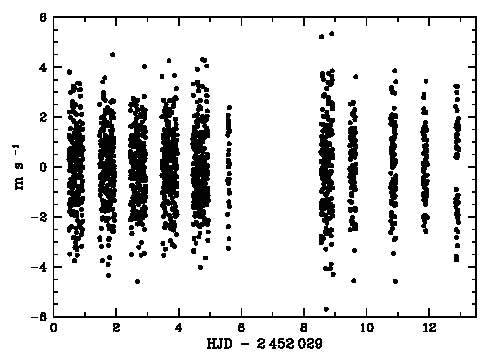
 Cen.
Cen.

Utiliser la TF pour la recherche de phénomènes périodiques.
Si l'on enregistre une série temporelle de 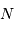 signaux, sur une durée totale
signaux, sur une durée totale 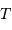 , l'analyse par transformée de Fourier se réécrit :
, l'analyse par transformée de Fourier se réécrit :
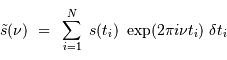
avec 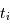 les dates individuelles et
les dates individuelles et 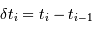 .
Si l'enregistrement est suffisamment régulier :
.
Si l'enregistrement est suffisamment régulier :
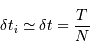
Les durées 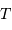 et
et 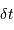 définissent les principales propriétés de l'analyse de Fourier.
définissent les principales propriétés de l'analyse de Fourier.
Un signal observé durant une durée totale 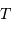 permet une résolution en fréquence
permet une résolution en fréquence 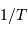 .
.
Un signal observé avec un échantillonnage 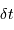 permet de suivre les fréquences jusqu'à la coupure
permet de suivre les fréquences jusqu'à la coupure 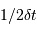 .
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
.
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
L'observation de phénomènes variables doit permettre :
Si l'on enregistre une série temporelle de 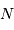 signaux, sur une durée totale
signaux, sur une durée totale 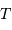 et avec un échantillonnage
et avec un échantillonnage 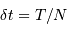 , on peut alors distinguer
sans ambiguïté
, on peut alors distinguer
sans ambiguïté 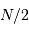 fréquences, entre
fréquences, entre 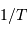 et
et 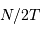 .
.
Pour une série temporelle, la résolution en fréquence du spectre est d'autant meilleure que la base de temps d'observation est plus longue.
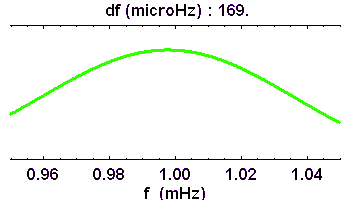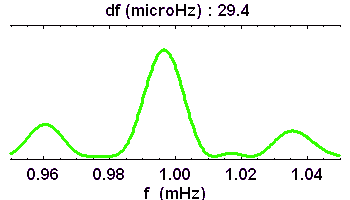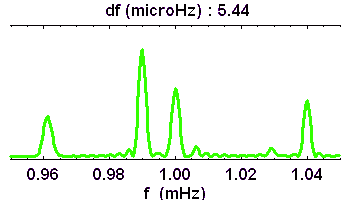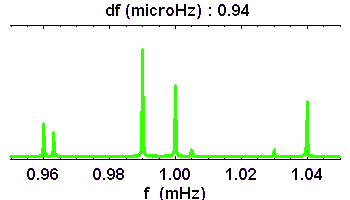
Pour une image, on relie la fréquence de coupure spatiale à la résolution spatiale .

Difficulté : ☆☆ Temps : 30 min
On échantillonne un signal temporel avec un pas de temps 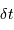 . On définit la pulsation
. On définit la pulsation 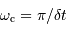 .
.
Montrer qu'il y a confusion entre les spectres de puissance des signaux périodiques de pulsation 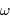 et
et
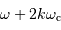 ou
ou 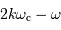 , où
, où 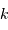 est un entier
est un entier
En déduire l'expression de la pulsation de coupure
Une analyse par TF va traiter différemment un signal, avec un spectre donné, d'un bruit, sans signature spectrale caractéristique.
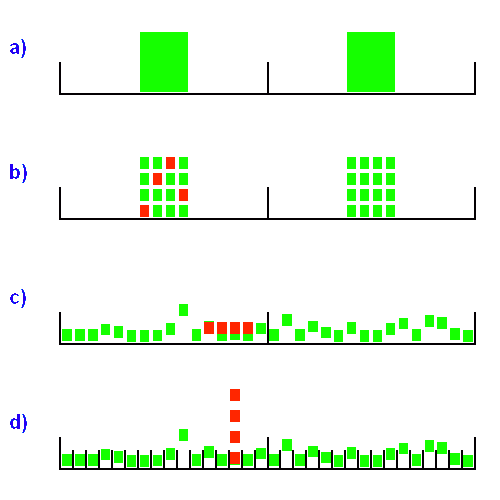
Un bruit gaussien ne montre aucune fréquence privilégiée, contrairement à un bruit en 1/f.
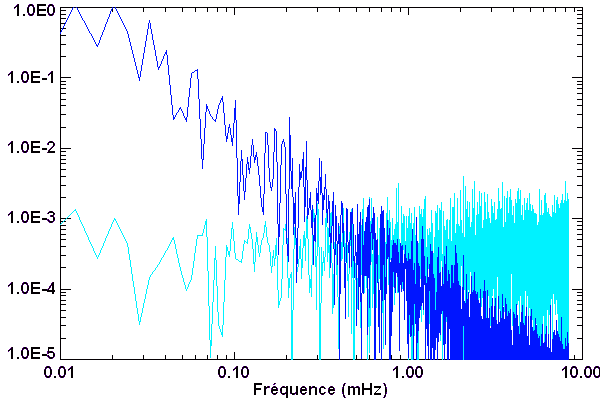
Utiliser la TF pour distinguer signaux et bruits
La dialectique est simple : un bruit ne mérite ce titre qu'en l'absence de signature spectrale définie (un bruit blanc ne présente aucune particularité spectrale; un bruit instrumental, par effet de mémoire, présente plus d'énergie aux basses fréquences qu'aux fréquences plus élevées).
La TF permet par son principe, en classant et en analysant les fréquences constitutives d'une suite de données, de distinguer la part du signal de celle du bruit. En pratique, cela nécessite un rapport signal-à-bruit suffisant (mais qui peut être très faible).
Lorsque le nombre de données observationnelles augmente, un signal cohérent va garder une signature bien précise. En revanche, un bruit va voir son énergie diluée dans une multitude de fréquences.
La TF permet de faire ressortir du bruit un signal bien cohérent.
En augmentant la durée totale de la série temporelle de données, un signal périodique cohérent (càd de durée de vie supérieure à la durée d'observation) ressort peu à peu du bruit.
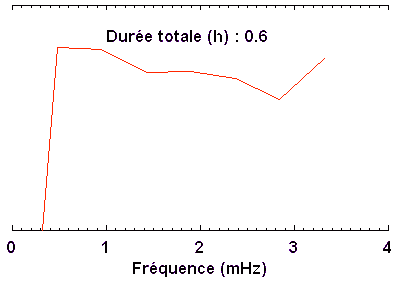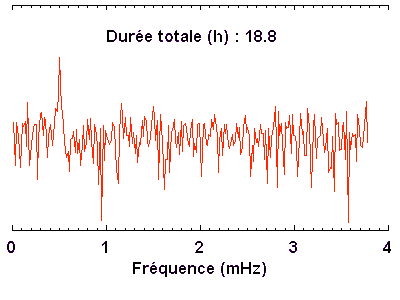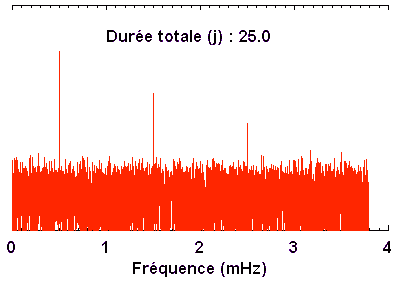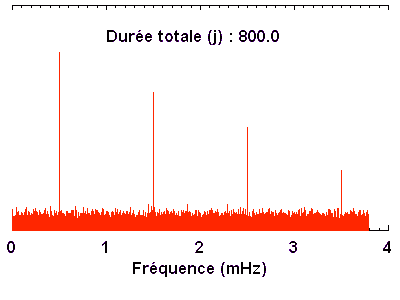
A l'aide de l'appliquette ci-dessous, on se propose d'évaluer comment le bruit évolue dans un spectre

Avec comme signal une sinusoïde, comme méthode la FT, et 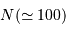 points dans l'échantillon, faire varier le niveau de bruit
points dans l'échantillon, faire varier le niveau de bruit 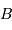 , et montrer que le signal est identifiable dans le spectre si son amplitude excède
largement
, et montrer que le signal est identifiable dans le spectre si son amplitude excède
largement 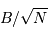 .
.
Si besoin, zoomer sur les hautes fréquences du spectre pour s'affranchir du fort signal à basse fréquence.
Difficulté : ☆☆☆ Temps : 30 min
La documentation de HARPS indique qu'un rapport signal à bruit de 500 sur un spectre correspond à une incertitude, exprimée en vitesse, de 45 cm/s. Par ailleurs, une cible de magnitude 5.5 conduit à un rapport signal à bruit de 200 avec des poses de 3 min. A quelle vitesse cela correspond-il ?
Combien de poses élémentaires sur une telle étoile sont nécessaires pour aboutir à un bruit résiduel de 5 cm/s. A quelle durée cela correspond-il ?
Sur la cible alphaCen B, très brillante, HARPS délivre un signal bruité à 2 cm/s, après 7 h d'observation. Les poses élémentaires étant de 1 min, quelle est la performance en vitesse sur une pose ?
pages_traiter/analyse-tf-sexercer.html
Avec les notations du cours.
Poser 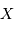 la dimension de la variable
la dimension de la variable 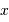 ,
, 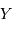 celle de la fonction
celle de la fonction 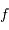 . Et en déduire les dimensions de
. Et en déduire les dimensions de 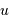 et
et 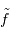
Avec les notations du cours, et en notant entre crochets les dimensions.
![[x] = X \mathrm{\ et\ } [f] = Y](../pages_traiter/equations_analyse-tf/equation30.png) , donc la définition de la TF donne :
, donc la définition de la TF donne :
![[u] = X^{-1} \hbox{ et } [\tilde f] = XY](../pages_traiter/equations_analyse-tf/equation31.png) .
.
On en déduit l'homogénéité :
![\left [\int \left| f (x) \right|^{2} \ {\mathrm{d}} x \right] \ =\ Y^2\ X \ =\ (YX)^2 \ X^{-1} \ =\ \left [\int \left| \tilde s (u) \right|^{2} {\mathrm{d}} u \right]](../pages_traiter/equations_analyse-tf/equation32.png)
Passer à la limite des grandes valeurs de 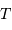 .
.
Avec un signal purement sinusoïdal d'amplitude 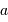 et de fréquence
et de fréquence 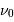 , la définition donne :
, la définition donne :
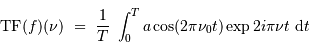
Pour 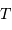 grand devant
grand devant 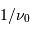 , si
, si 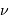 est différent de
est différent de 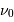 , l'intégrale tend vers 0, alors que pour
, l'intégrale tend vers 0, alors que pour 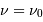 , on retrouve :
, on retrouve :
![\mathrm{TF} (f) (\nu_0) \ =\ {1\over T}\ \int_0^T {a\over 2} [\exp 2i\pi \nu_0 t + \exp -2i\pi \nu_0 t]\ \exp 2i\pi \nu_0 t \ {\mathrm{d}} t \ ={1\over T}\ \int_0^T {a\over 2} \ {\mathrm{d}} t \ = {a\over 2}](../pages_traiter/equations_analyse-tf/equation44.png)
Au facteur 1/2 près, dû au fait que la TF en 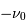 est également non nul,
la normalisation en
est également non nul,
la normalisation en 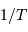 par rapport à la définition de la TF usuelle permet de retrouver dans le spectre l'amplitude du signal sinusoïdal.
par rapport à la définition de la TF usuelle permet de retrouver dans le spectre l'amplitude du signal sinusoïdal.
Ecrire la relation de Parseval-Plancherel et faire le changement de variable de 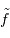 à
à 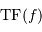 .
.
Avec les notations analogues au cours 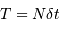 , et en tenant compte des propriétés de la TF, on a :
, et en tenant compte des propriétés de la TF, on a :
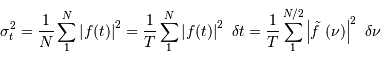
en se servant de la relation de Perseval, et du fait que l'énergie est rapportée sur 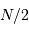 fréquences réelles entre les fréquences nulle et
fréquences réelles entre les fréquences nulle et 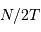 .
Avec le changement de notation :
.
Avec le changement de notation : 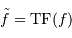 , et en tenant compte de
, et en tenant compte de 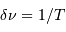 :
:
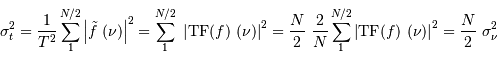
On en déduit :
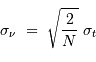
Le bruit dans le spectre de Fourier diminue comme la racine carrée du nombre de points de mesure.
pages_traiter/analyse-tf-signal-sexercer.html
Courage, ce n'est qu'un peu de calculs sur les sinus.
Estimer 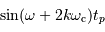 à une date
à une date 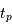 de l'échantillonnage
de l'échantillonnage
Supposer 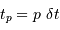
On suppose, sans restreindre la généralité, que le signal est de forme sinusoïdale, et l'on choisit l'origine des temps de façon à avoir la p-ième date de l'échantillon vérifiant 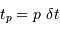 .
.
On en déduit :
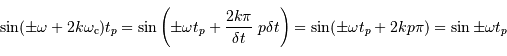
Au signe près, auquel n'est pas sensible le spectre de puissance (TF ),
cette égalité est assurée à toute date de l'échantillonnage.
),
cette égalité est assurée à toute date de l'échantillonnage.
Jusqu'à quelle fréquence n'y aura-t-il pas de confusion?
La 1ère confusion va apparaître pour les pulsations 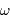 telles que
telles que
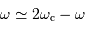 , càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.
, càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.
pages_traiter/analyse-tf-bruit-sexercer.html
L'incertitude en vitesse correspond à un niveau de bruit.
Le niveau de bruit et le rapport signal à bruit sont simplement ... inversement proportionnels
Le niveau de signal est inversement proportionnel au rapport signal à bruit.
La performance 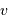 avec un rapport signal à bruit de 200 vérifie donc :
avec un rapport signal à bruit de 200 vérifie donc :
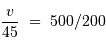
D'où le niveau de bruit : 110 cm/s.
Le rapport signal à bruit évole comme la racine carrée du nombre de pose élémentaire,
Le rapport signal à bruit évoluant comme la racine carrée du nombre 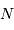 de pose élémentaire, ce dernier doit vérifier :
de pose élémentaire, ce dernier doit vérifier :
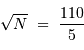
Soit 484 poses élémentaires de 3 minutes, soit environ 24 h de données. Elles ne pourront être atteintes qu'en 3 nuits environ.
7 h font combien de minutes ?
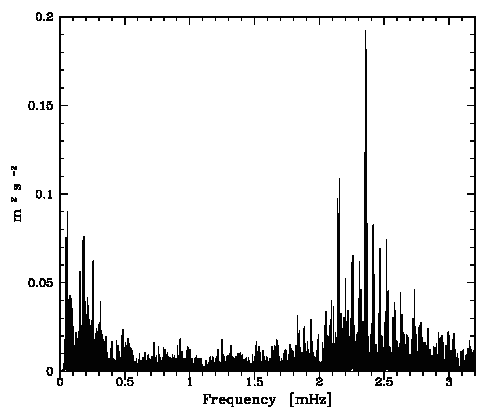
La nuit d'observation de 7 h comprend 420 poses élémentaires de 1 min. Le rapport signal à bruit évoluant comme la racine carrée du nombre de pose élémentaire, la performance en 1 min vaut :