Se repérer
Les cartes du ciel ci-jointes repèrent
les étoiles les plus brillantes par 2 coordonnées angulaires, pour 2 régions du ciel, sur l'équateur céleste ou proche du pôle nord céleste.
L'une de ces coordonnées angulaires, appelée ascension droite,
est exprimée en unités horaires (h, min, s).
La pleine échelle vaut 24 h, équivalant à 1
tour de ciel, ou 360 degrés.
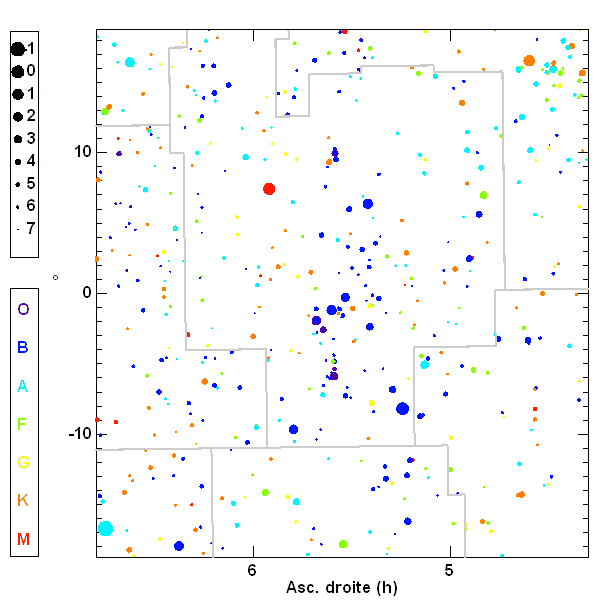
Carte du ciel, dans la région d'Orion. Les étoiles sont repérées par leurs coordonnées équatoriales (ascension droite en abscisse, déclinaison en ordonnée), analogues aux coordonnées géographiques (longitude, latitude) utilisées pour un lieu sur Terre.
Magnitudes
et
types spectraux sont également indiqués.
Crédit :
BSC/ASM
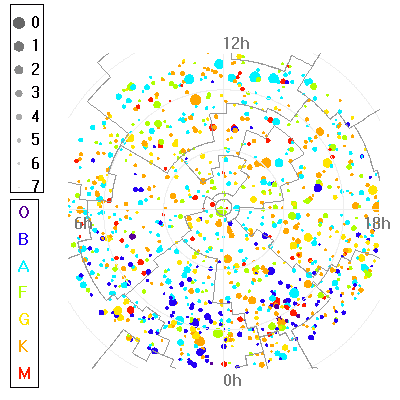
Carte du ciel, autour de l'étoile polaire. Les étoiles sont repérées par leurs coordonnées équatoriales, analogues aux coordonnées géographiques (longitude, latitude) utilisées pour un lieu sur Terre.
Crédit :
BSC/ASM

Carte des constellations de l'hémisphère Nord. On y reconnaît la Grande Ourse,
le Lion, le Triangle, les Gémeaux...
Crédit :
Bibliothèque de l'Observatoire de Paris
Constellations
Les constellations réunissent de façon arbitraire des étoiles voisines. Les histoires que racontent les constellations ou les groupes de constellation offrent un support à la mémoire.
Les tracés de constellation peuvent joindre les étoiles (la Grande Ourse devenant ainsi une casserole), ou peuvent les délimiter (les représentations du cours ont choisi cette convention de l'Union Astronomique Internationale).
Coordonnées équatoriales
Le ciel, sans la dimension de profondeur, est analogue à la surface d'une sphère. Usuellement,
on y repère un astre par son ascension droite et sa déclinaison. Ces 2 coordonnées sont définies dans un repère lié à la Terre : un des axes s'appuie sur l'axe polaire terrestre, l'autre sur l'équateur.
La déclinaison, équivalant à la latitude, varie de -90 à +90 degrés,
ces limites pointant respectivement les pôle sud et nord célestes.
L'ascension droite est comptée en heure, minute et seconde.
L'origine des ascensions droites est la direction du point vernal.
La conversion entre heure, minute et seconde d'une part, et degré,
minute d'arc et seconde d'arc d'autre part, est donnée par la
table ci-jointe.
La conversion entre heure, minute et seconde d'une part, et degré, minute d'arc et seconde d'arc d'autre part, est donnée par la table ci-jointe qui propose une conversion entre les unités horaires et angulaires. Le facteur 15 provient simplement de la division du jour (1 tour, ou 360 deg), en 24 heures, soit une rotation de 15 deg/h. Attention à bien respecter les unités, afin de ne pas confondre minute horaire et minute angulaire, qui ne sont pas égales.
Conversions angulaires
| 1 heure = 15 deg | 1 deg = 4 min | 1 deg = 0.0174 rad |
| 1 minute= 15' | 1 ' = 4 s | 1' = 0.29 mrad |
| 1 seconde= 15" | 1" = 1/15 s | 1" = 5 microrad |
Ecriture
Il est nécessaire de distinguer l'écriture décimale de l'écriture développée dans ces systèmes d'unités qui reposent sur une base non décimale.
Par exemple : 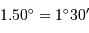 , mais
, mais 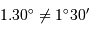
Conversion en radian
L'unité angulaire dans le système international d'unités (SI) est le radian. Vu l'usage intensif de la seconde d'arc en astronomie, il est utile d'avoir en tête l'ordre de grandeur :
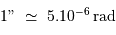
Cartographie
Exemple d'utilisation de l'appliquette : galaxie NGC1316, elliptique, en train de cannibaliser une petite galaxie elliptique.

Coordonnées
A l'aide du curseur, estimer les coordonnées angulaires des points du champ dans la constellation d'Orion, pour en déduire l'ordre de grandeur de ses dimensions angulaires.

Vérifier l'accord avec les coordonnées 2000 de 4 objets du champ, et repérer la nébuleuse d'Orion M42.
| étoile | 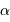 (h, min, s) (h, min, s) | 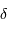 (deg, ', ") (deg, ', ") |
| Bételgeuse | 05 55 10 | +07 24 25 |
| Rigel | 05 14 32 | -08 12 06 |
| Bellatrix | 05 25 08 | +06 20 59 |
| M 42 | 05 35 17 | -05 23 28 |
Carte du ciel
Reprendre le relevé pour la carte synthétique de la région d'Orion.
Pourquoi l'accord est-il meilleur ?

 Un tour de ciel
Un tour de ciel
Difficulté : ☆
Temps : 20 min
En unité naturelle angulaire, le ciel, comme toute sphère, couvre 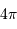 stéradians (pour s'en convaincre si besoin est, se rappeler l'aire de la sphère de rayon
stéradians (pour s'en convaincre si besoin est, se rappeler l'aire de la sphère de rayon 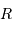 ). L'astronome préfère exprimer les angles en degré, heure et minute d'angle
). L'astronome préfère exprimer les angles en degré, heure et minute d'angle 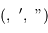 . Les instruments astronomiques ont des champs de vue qui varient typiquement de
. Les instruments astronomiques ont des champs de vue qui varient typiquement de 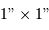 à
à 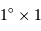 pour les instruments grand champ.
pour les instruments grand champ.
Question 1)
Traduire 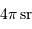 en degré carré, puis en minute et seconde carrée.
en degré carré, puis en minute et seconde carrée.
1 stéradian représente un angle solide de 1 radian par 1 radian : 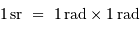
Ne pas oublier que :
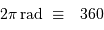 °
°
Question 2)
Un instrument imageur couvre un champ carré de 12' de côté (projet DENIS, mené à l'Observatoire Austral Européen (ESO), pour la cartographie infrarouge du ciel austral). Il pose en 3
couleurs dans l'infrarouge (filtres I, J, K à respectivement 0.85, 1.25 et 2.15 micromètres), avec des temps de pose de l'ordre de 10 à 30 s, soit environ 1 minute pour les 3 filtres. Il permet ainsi de cartographier une moitié du
ciel, jusqu'aux magnitudes limites 18.5 à 14.
Estimer la durée du programme d'observation (5 h/nuit pour compter
les aléas divers et météorologiques).
Se servir de la question précédente
 Détails lunaires
Détails lunaires
Difficulté : ☆☆
Temps : 20 min
La surface de la Lune a été observée par le système d'optique adaptative (OA) de l'ESO. Les clichés ci-joints permettent de comparer l'apport de cette technique. La largeur totale du champ représente 26", pour 201 pixels.
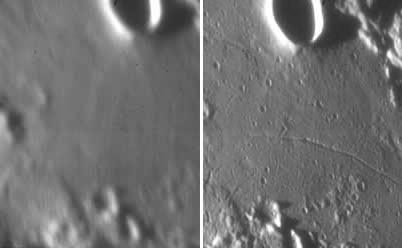
Avec optique adaptative (à droite), la surface de la Lune présente des détails inaccessibles sur l'image non corrigée
(système d'OA NAOS, développé pour le VLT à l'ESO). La largeur totale du champ représente 26".
Crédit :
ESO

Question 1)
Quelle est la taille angulaire d'un pixel ? En déduire la taille
linéaire, en km, du champ de vue d'un pixel et du champ de vue
total, la Lune étant à 384 000 km de la Terre lors de
l'observation.
[2 points]
L'unité naturelle des angles est le radian.
Question 2)
À l'aide de l'appliquette, estimer le diamètre apparent du gros cratère, les tailles des plus petits détails visibles, avec ou sans optique adaptative.
[1 points]
La conversion d'unité peut être introduite dans la fenêtre rapport d'unité.
- Question 1
Aide :
1 stéradian représente un angle solide de 1 radian par 1 radian : 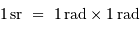
Aide :
Ne pas oublier que :
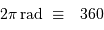 °
°
Solution :
Avec les égalités :
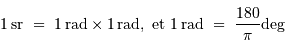
il vient
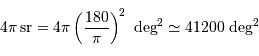
En multipliant par 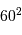 , on trouve
, on trouve 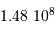 minutes d'angle
carrées, et
minutes d'angle
carrées, et 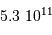 secondes d'angle carrées.
secondes d'angle carrées.
- Question 2
Aide :
Se servir de la question précédente
Solution :
Le ciel entier couvrant 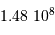 minutes d'angle
carrées, un hémisphère représente
minutes d'angle
carrées, un hémisphère représente 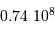 champs de 1' par 1', soit
champs de 1' par 1', soit
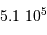 champs de 12' par 12'.
champs de 12' par 12'.
Chaque champ nécessite 1 min de pose, soit un programme de 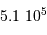 minutes, ou de l'ordre de 8400 h.
minutes, ou de l'ordre de 8400 h.
Il faut compter, avec des nuits de 5 h efficaces,
si l'on néglige tout temps mort (changement de filtres, dépointages...),
1680 nuits, soit un programme de 4.6 années



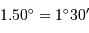 , mais
, mais 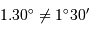
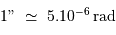

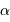 (h, min, s)
(h, min, s) 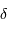 (deg, ', ")
(deg, ', ") 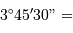
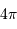 stéradians (pour s'en convaincre si besoin est, se rappeler l'aire de la sphère de rayon
stéradians (pour s'en convaincre si besoin est, se rappeler l'aire de la sphère de rayon 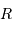 ). L'astronome préfère exprimer les angles en degré, heure et minute d'angle
). L'astronome préfère exprimer les angles en degré, heure et minute d'angle 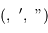 . Les instruments astronomiques ont des champs de vue qui varient typiquement de
. Les instruments astronomiques ont des champs de vue qui varient typiquement de 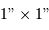 à
à 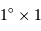 pour les instruments grand champ.
pour les instruments grand champ.
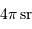 en degré carré, puis en minute et seconde carrée.
en degré carré, puis en minute et seconde carrée.
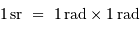
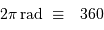 °
°

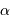 petite correspond, à une distance
petite correspond, à une distance 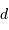 , à la taille linéaire
, à la taille linéaire 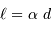 . Mais il faut travailler dans le bon système d'unités.
. Mais il faut travailler dans le bon système d'unités.
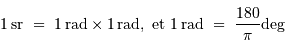
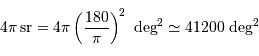
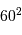 , on trouve
, on trouve 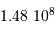 minutes d'angle
carrées, et
minutes d'angle
carrées, et 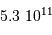 secondes d'angle carrées.
secondes d'angle carrées.
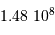 minutes d'angle
carrées, un hémisphère représente
minutes d'angle
carrées, un hémisphère représente 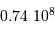 champs de 1' par 1', soit
champs de 1' par 1', soit
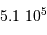 champs de 12' par 12'.
champs de 12' par 12'.
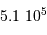 minutes, ou de l'ordre de 8400 h.
minutes, ou de l'ordre de 8400 h.