Visibilité des éclipses de Soleil
Auteur: P. Rocher - IMCCE - Observatoire de Paris
- Introduction
- Quand ont lieu les éclipses de Soleil ?
- Introduction
- Le mouvement moyen de la ligne des noeuds
- Le mouvement moyen de la ligne des noeuds-2
- En savoir plus: Le calcul de la saison des éclipses
- En savoir plus: Le mouvement réel de la ligne des noeuds
- Le critère en latitude
- Les bornes du critère en latitude
- En savoir plus: La parallaxe solaire et la parallaxe lunaire
- En savoir plus: La démonstration du critère en latitude
- En savoir plus: Critère en latitude-3
- En savoir plus: Critère en latitude-4
- En savoir plus: Critère en latitude-5
- En savoir plus: Critère en latitude-6
- Critère en longitude
- Nombres d'éclipses de Soleil ?
- Introduction
- Nombre d'éclipses à chaque saison d'éclipses
- Nombre d'éclipses à chaque saison d'éclipses-2
- Nombre d'éclipses à chaque saison d'éclipses-3
- Nombre d'éclipses par an
- Nombre d'éclipses par an-2
- Nombre d'éclipses par an-3
- Les séries courtes d'éclipses
- Les séries courtes d'éclipses-2
- Les séries courtes d'éclipses-3
- Répartition des éclipses sur une période de 22 ans
- exercice eclipse soleil
- Canons et grandeurs des éclipses de Soleil
- Introduction
- Les canons d'éclipses de Soleil
- En savoir plus: Le canon de l'IMCCE : les théories utilisées
- En savoir plus: Le canon de l'IMCCE : les paramètres physiques
- En savoir plus: Le canon de l'IMCCE : les résultats
- Les éclipses totales les plus longues
- Les éclipses totales les plus longues-2
- Les éclipses annulaires les plus longues
- Les éclipses partielles les plus petites
- L'éclipse de 651
- L'éclipse de 1327
- Les éclipses récentes et futures
- Introduction
- Les éclipses totale entre 1998 et 2020
- Les éclipses annulaires entre 1998 et 2020
- Fréquence des éclipses centrales de Soleil en France
- Fréquence des éclipses centrales de Soleil en France-2
- Eclipses du XVI, XVII et XVIIIème siècles, visibles en France
- Eclipses du XIX et du XXème siècles visibles en France
- Eclipses du XXI siècle visibles en France
- Observation d'une éclipse de Soleil
- Introduction
- Précautions à prendre pour observer une éclipse de Soleil
- Précautions à prendre pour observer une éclipse de Soleil-2
- Précautions à prendre pour observer une éclipse de Soleil-3
- L'utilisation de filtres pour l'observation des éclipses
- L'utilisation de filtres pour l'observation des éclipses-2
- L'utilisation de filtres pour l'observation des éclipses-3
- L'utilisation de filtres pour l'observation des éclipses-4
- Les traumatismes causés par le Soleil
Introduction
 Introduction
Introduction
Après avoir étudié la géométrie des éclipses de Soleil, nous allons répondre à la question : quand ont lieu les éclipses de Soleil? Pour cela nous allons définir la ligne des noeuds de l'orbite lunaire et nous allons étudier son mouvement.
 Prérequis
Prérequis
Les éclipses de Soleil.
Quand ont lieu les éclipses de Soleil ?
Introduction
 Introduction
Introduction
Dans cette section nous définissons la ligne des noeuds de l'orbite lunaire et nous étudions son déplacement angulaire moyen dans le plan de l'écliptique. Puis, nous définissons la fréquence avec laquelle le Soleil apparent passe dans la direction de la ligne des noeuds (la saison des éclipses).
Nous définissons ensuite un critère portant sur la latitude de la Lune au moment de sa conjonction avec le Soleil, pour savoir s'il y a ou non une éclipse de Soleil. Nous donnons les bornes de ce critère en fonction du type d'éclipse observable.
Enfin nous transposons ce critère sur la latitude lunaire en un critère sur la différence de longitude entre la longitude de la conjonction et la longitude du noeud lunaire.
Les parties pour en savoir plus vous montre comment calculer la valeur moyenne de la saison d'éclipse, puis nous explique le mouvement réelle de cette ligne. Nous donnons également la démonstration des critères en latitude.
Le mouvement moyen de la ligne des noeuds
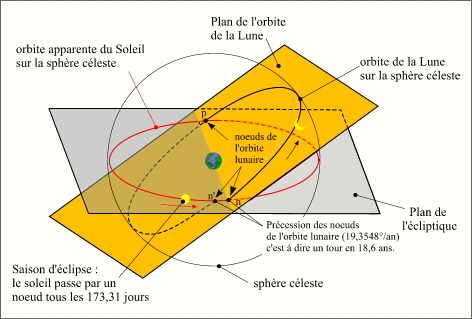
Orbite de la Lune, mouvement de la ligne des noeuds.
Crédit : IMCCE/Patrick Rocher
Il y a éclipse de Soleil lorsque la Terre passe dans le cône d'ombre ou dans le cône de pénombre de la Lune. Le Soleil, la Lune et la Terre sont alors presque alignés, et on est au voisinage de la nouvelle Lune (conjonction). Si le plan de l'orbite de la Lune était le même que le plan de l'orbite de la Terre (écliptique), il y aurait une éclipse de Soleil à chaque nouvelle Lune, or le plan de l'orbite de la Lune est incliné d'environ 5° 17' sur le plan de l'orbite terrestre à la nouvelle Lune. À chaque instant, l'intersection de ces deux plans est une droite appelée ligne des noeuds et les intersections de cette droite avec l'orbite de la Lune sont appelées noeuds de l'orbite lunaire.
Le mouvement moyen de la ligne des noeuds-2
Cette ligne des noeuds n'est pas fixe, elle est animée, dans le sens rétrograde (sens des aiguilles d'une montre), d'un mouvement de précession d'une période de 18,6 ans, soit un déplacement moyen de 19,354 8° par an.
Pour qu'il y ait une éclipse il faut donc, dans le repère écliptique géocentrique, que la direction Terre-Soleil soit près de la ligne des noeuds lunaires au moment de la nouvelle Lune. Compte tenu du mouvement moyen de précession des noeuds, le Soleil apparent passe en moyenne par l'un des deux noeuds tous les 173,31 jours. Cette période porte le nom de saison des éclipses. Il passe par le même noeud tous les 346,62 jours, cette période porte le nom d'année des éclipses.
En savoir plus: Le calcul de la saison des éclipses
 En savoir plus
En savoir plus
La direction Terre-Soleil est la direction du Soleil apparent vu depuis la Terre, elle fait donc 360° pendant une révolution sidérale de la Terre. La ligne des noeuds de l'orbite lunaire se déplace en moyenne de 19,3413618°/an dans le sens rétrograde. On a donc deux mouvements en sens contraire. La période T qui ramène le Soleil apparent dans la direction d'un même noeud de l'orbite lunaire est solution de l'équation suivante :
T . 360°/an + T . 19,3413618°/an = 360°
ce qui donne T = 360/(360 + 19,3413618) an = 0,9490133 an.
L'année sidérale étant égale à : an = 365,2563632 jours, T = 346,63 jours.
La saison des éclipses correspond à l'intervalle de temps mis par le Soleil apparent pour passer d'un noeud de l'orbite lunaire à l'autre, elle est donc égale à T/2 ~ 173,31 jours.
La valeur de cette période T nous permet de calculer la vitesse moyenne du Soleil apparent (ou de la Terre) dans un repère tournant lié à la ligne des noeuds de l'orbite lunaire. Par rapport à cette ligne des noeuds le Soleil apparent fait un tour de 360° en 346,63 jours, sa vitesse moyenne par rapport à la ligne des noeuds est donc de 360°/346,63j = 1,038°/jour.
En savoir plus: Le mouvement réel de la ligne des noeuds
 En savoir plus
En savoir plus
En réalité, le mouvement rétrograde de la ligne des noeuds présente des inégalités importantes. À certaines époques, sa vitesse est le double de la moyenne. À d'autres moments, sa vitesse est presque nulle, les noeuds sont alors quasi stationnaires. Cela se produit aux voisinages du passage du Soleil dans la direction de la ligne des noeuds, donc au voisinage des éclipses de Soleil (et aussi de Lune). On peut expliquer ce phénomène de la manière suivante, lorsque le Soleil est sur la ligne des noeuds, il se trouve dans le plan de l'orbite de la Lune, la force perturbatrice du Soleil est alors comprise dans le plan de l'orbite de la Lune, donc la composante perpendiculaire à ce plan est nulle et ne "tire" pas sur le plan de l'orbite. Le fait que les noeuds soient quasi-stationnaires au moment des éclipses est très important, en effet les positions moyennes des noeuds sont alors presque égales aux positions vraies, donc dans l'étude des éclipses on peut utiliser le mouvement moyen des noeuds.
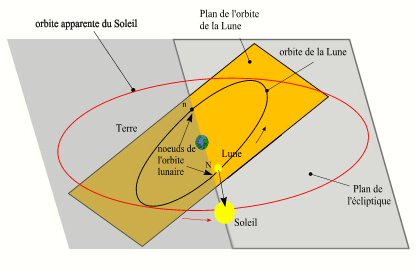
Système Terre - Lune - Soleil lorsque le Soleil est sur la ligne des noeuds
Crédit : IMCCE/Patrick Rocher
Le critère en latitude
On démontre qu'une éclipse de Soleil se produira si, au moment de la nouvelle Lune (instant où les longitudes géocentriques de la Lune et du Soleil sont égales, c'est-à-dire au moment de la conjonction en longitude), la valeur absolue de la différence b des latitudes géocentriques apparentes du centre de la Lune et du centre du Soleil est inférieure à 1,41° (1° 24' 37"), elle se produira peut-être si elle est comprise entre 1,41° (1° 24' 37") et 1,58° (1°34' 46") et elle ne se produira pas si elle est supérieure à 1,58° (1° 34' 46").
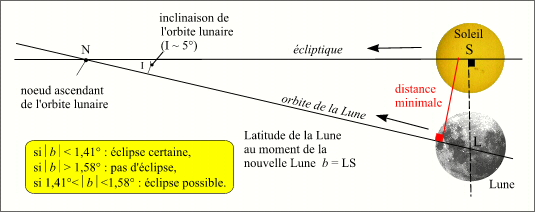
Critères en latitude pour les éclipses de Soleil (vu depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Sur la figure ci-contre, la distance minimale correspond à l'instant où pour un observateur terrestre, le centre de la Lune est le plus près possible du centre du Soleil, cela correspond si l'éclipse a lieu, au maximum de l'éclipse. Durant une éclipse de Soleil on a toujours un des deux scénarii suivants :
- si l'éclipse a lieu avant le passage de la Lune au noeud, on observe d'abord la conjonction (nouvelle Lune), puis le maximum de l'éclipse, puis le passage au noeud,
- si l'éclipse a lieu après le passage de la Lune au noeud, on observe d'abord le passage au noeud, puis le maximum de l'éclipse et enfin la conjonction.
La géométrie de ce dessin montre également que plus la conjonction est proche du noeud, plus la distance minimale entre la Lune et le Soleil est petite et plus la magnitude de l'éclipse est grande. Ainsi, les éclipses partielles correspondent à des conjonctions situées loin des noeuds de l'orbite lunaire et les éclipses centrales (annulaires, totales ou mixtes) correspondent à des conjonctions proches des noeuds de l'orbite lunaire. On rappelle que le fait qu'une éclipse centrale soit annulaire, totale ou mixte ne dépend pas de la distance de la conjonction aux noeuds de l'orbite lunaire, mais dépend uniquement des tailles des diamètres apparents des corps, donc de leurs positions sur leur orbite.
Les bornes du critère en latitude
On peut détailler le critère en latitude en déterminant pour quelle valeur de b (0,88°) on a une éclipse centrale avec certitude et pour quelle valeur de b (1,05°) on n'a pas d'éclipse centrale avec certitude (mais une éclipse partielle avec certitude), ces valeurs sont données dans le graphique ci-contre.
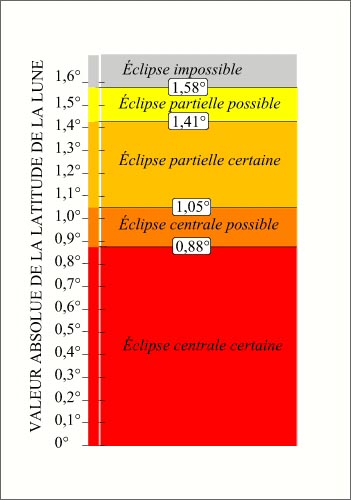
Crédit : IMCCE/Patrick Rocher
On peut également calculer les valeurs moyennes de ces critères en latitude. Pour avoir une éclipse de Soleil il faut que b soit inférieure à 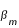 = 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à
= 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à  = 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
= 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
En savoir plus: La parallaxe solaire et la parallaxe lunaire
 En savoir plus
En savoir plus
La démonstration du critère en latitude fait intervenir la notion de parallaxe équatoriale solaire et de parallaxe équatoriale lunaire, il convient donc de les définir.
La parallaxe équatoriale solaire est égale à l'angle sous lequel un observateur situé au centre du Soleil voit le rayon terrestre, de même la parallaxe équatoriale lunaire est l'angle sous lequel un observateur situé au centre de la Lune voit le rayon terrestre. C'est également la différence angulaire sous laquelle deux observateurs, l'un situé au centre de la Terre, l'autre situé sur la Terre et observant la Lune à l'horizon, voient le centre de la Lune.
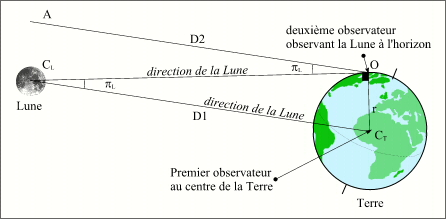
La parallaxe équatoriale lunaire
Crédit : IMCCE/Patrick Rocher
Comme on le constate sur la figure, les deux droites D1 et D2 étant parallèles les angles AOCL et OCLCT sont des angles alternes internes, donc égaux. Ainsi, si les éphémérides donnent une direction angulaire géocentrique de la Lune b, un observateur qui regarde la Lune à l'horizon, la voit dans la direction b -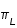 .
.
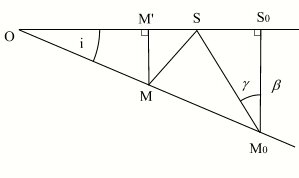
La parallaxe se calcule par la formule : 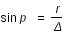 ,
, 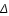 étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
En savoir plus: La démonstration du critère en latitude
 En savoir plus
En savoir plus
Nous allons établir le critère en latitude dans le cas d'une éclipse au noeud ascendant de l'orbite lunaire, la conjonction ayant lieu avant le passage au noeud. La démonstration est identique pour un passage au noeud descendant ou avec une conjonction située après le passage au noeud, la seule chose qui change dans ce dernier cas est la position du minimum de distance entre des deux corps.
Critère en latitude
Crédit : IMCCE/Patrick Rocher
Soit M0 et S0 : les positions de la Lune et du Soleil à l'instant de la conjonction (nouvelle Lune) avant le passage de la Lune au noeud ascendant de son orbite.
M et S : les positions de la Lune et du Soleil à un instant t postérieur à la conjonction.
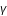 : l' angle S0M0S.
: l' angle S0M0S.
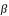 : la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
: la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
q : rapport du mouvement en longitude de la Lune sur celui du Soleil.
Le calcul du critère en latitude consiste à calculer le minimum de la distance SM (corrigé des parallaxes équatoriales lunaire et solaire) et de le comparer avec la somme des demi-diamètres apparents du Soleil et de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore.
En savoir plus: Critère en latitude-3
 En savoir plus
En savoir plus
On a :
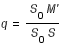 soit
soit 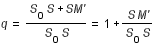
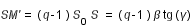 avec
avec 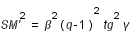
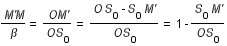
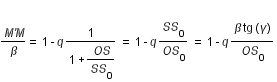
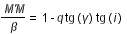
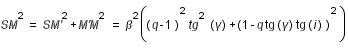 (1)
(1)
On introduit un angle auxiliaire i', tel que : 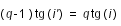
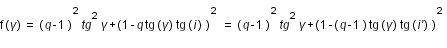
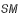 est minimum lorsque
est minimum lorsque 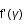 la dérivée de f est nulle
la dérivée de f est nulle
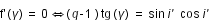 (2)
(2)
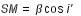 (3)
(3)
En savoir plus: Critère en latitude-4
En savoir plus: Critère en latitude-5
 En savoir plus
En savoir plus
Le tableau suivant donne les valeurs extrêmes des paramètres, l'étude des séries donnant l'orbite de la Lune, montre qu'au voisinage de la nouvelle Lune (et de la pleine Lune) la valeur de l'inclinaison est maximale, il convient donc de prendre i ~ 5° 17' dans ces formules.
Valeurs extrêmes et moyennes des paramétres
| Paramètres |
Maximum |
Minimum |
Moyenne |
| q |
16,2 |
10,9 |
13,5 |
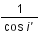
|
1,0052 |
1,0043 |
1,00472 |
Parallaxe de la Lune 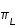
|
61' 27" |
53' 53" |
57' 2,70" |
Parallaxe du Soleil 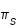
|
8,96" |
8,65" |
8,80" |
Demi-diamètres de la Lune 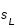 |
16' 45" |
14' 41" |
15' 32,58" |
Demi-diamètres du Soleil 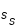
|
16' 18" |
15' 46" |
15' 59,63" |
Valeurs extrêmes et moyennes des paramètres.
En savoir plus: Critère en latitude-6
 En savoir plus
En savoir plus
Le critère en latitude s'écrit donc :
si 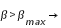 pas éclipse
pas éclipse
si 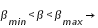 éclipse possible
éclipse possible
si 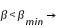 éclipse certaine
éclipse certaine
Si l'on utilise les paramètres du tableau précèdent on trouve 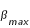 = 1° 34' 45,69" et
= 1° 34' 45,69" et 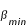 =1° 24' 37,31" et une valeur moyenne
=1° 24' 37,31" et une valeur moyenne 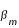 = 1° 28' 51" soit environ 1,48°.
= 1° 28' 51" soit environ 1,48°.
Le critère pour la centralité se calcule d'une manière analogue, il suffit de remplacer la somme des demi-diamètres apparents par la différence des demi-diamètres apparents dans l'équation (5). On obtient alors 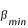 = 0° 52' 55,47" (soit environ 0,88°) et
= 0° 52' 55,47" (soit environ 0,88°) et 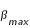 = 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne
= 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne 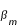 = 0° 56' 42,84" (environ 0,95°).
= 0° 56' 42,84" (environ 0,95°).
Critère en longitude
Le critère sur la latitude du centre de la Lune, peut se traduire en un critère sur la longitude de la conjonction Lune Soleil (donc la longitude) du Soleil par rapport au noeud de l'orbite lunaire. Ainsi il y aura éclipse si au moment de la conjonction en longitude, la différence de longitude entre le noeud de l'orbite lunaire et la longitude du Soleil est inférieure à 15,665°, il n'y aura pas d'éclipse si cette différence est supérieure à 17,375°, et il y aura peut-être éclipse si elle est comprise entre ces deux valeurs. Comme on le voit le critère en longitude est beaucoup plus large en amplitude que le critère en latitude, cela s'explique par la faible valeur de l'inclinaison de l'orbite lunaire.
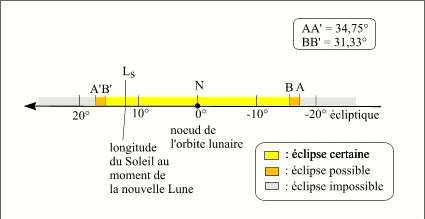
Critère en longitude pour les éclipses de Soleil (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
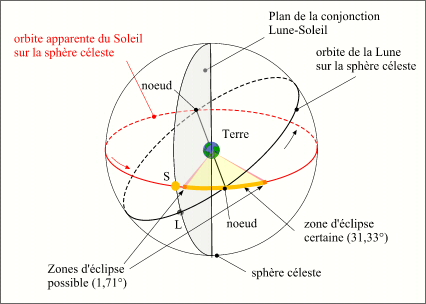
Critère en longitude pour les éclipses de Soleil (vu depuis l'espace)
Crédit : IMCCE/Patrick Rocher
Nombres d'éclipses de Soleil ?
Introduction
 Introduction
Introduction
Maintenant que nous avons défini des critères en latitude ou en longitude pour savoir s'il y a ou non des éclipses de Soleil, nous verrons qu'il y a obligatoirement ou moins une éclipse de Soleil à chaque saison d'éclipse et qu'il en est de même pour les éclipses de Lune. Nous donnons ensuite le nombre d'éclipses possibles sur une année solaire de 365 ou 366 jours.
Enfin nous étudions l'évolution du type des éclipses qui se succèdent d'une saison d'éclipse à la suivante. Pour compléter cette étude nous donnons et commentons un graphique représentant toutes les éclipses de Lune et de Soleil sur une période de 22 ans.
Nombre d'éclipses à chaque saison d'éclipses
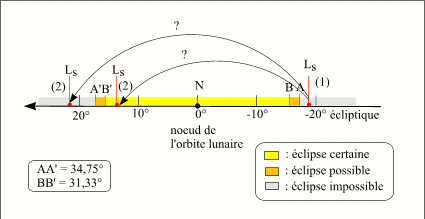
Critère en longitude pour les éclipses de Soleil (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
En étudiant la figure ci-contre, on peut se poser la question suivante. Supposons que nous ayons une conjonction en longitude (1) juste avant le point A, la conjonction suivante (2) va-t-elle être à l'intérieur ou à l'extérieur de l'arc BB' ? Pour répondre à cette question, on doit calculer de combien avance la longitude de la Terre (ou du soleil apparent) par rapport au noeud de l'orbite lunaire durant une révolution synodique de la Lune (une lunaison). On a vu que la Terre (ou le Soleil apparent) passe par le même noeud de l'orbite lunaire tous les 346,62 jours, donc la vitesse de la Terre par rapport à la ligne des noeuds est de 360°/346,64jours = 1,0386°/jour. Or la révolution synodique moyenne de la Lune est de 29,53 jours, donc entre deux conjonctions consécutives la longitude de la Terre varie de 1,0386 x 29,53 = 30,67°.
Or cette valeur est inférieure à la valeur de l'arc qui est égale à 31,33°. Donc à chaque passage de la Terre (ou du soleil apparent) par un noeud de l'orbite lunaire il y a obligatoirement une éclipse de Soleil au voisinage de la conjonction dont la longitude est la plus proche du noeud de l'orbite lunaire.
Nombre d'éclipses à chaque saison d'éclipses-2
Au moins deux éclipses (Lune et Soleil)
On peut donner une information supplémentaire, comme le critère en longitude est le même pour les éclipses de Lune, une demi-lunaison avant ou après la conjonction (nouvelle Lune) la Lune est en opposition (pleine Lune) et la Terre n'a parcouru que 15,335° en longitude par rapport au noeud, ces 15,335° correspondent à l'écart angulaire entre une conjonction et une opposition. Donc si une conjonction se trouve dans l'arc BB' l'opposition suivante ou l'opposition précédente se trouve obligatoirement aussi sur cet arc et il y a une éclipse de Lune, mais à l'autre noeud de l'orbite lunaire.
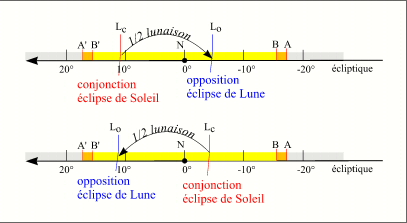
Conjonction et opposition au voisinage du noeud
Crédit : IMCCE/Patrick Rocher
À chaque saison d'éclipse, il y obligatoirement deux éclipses, une éclipse de Soleil et une éclipse de Lune.
Nombre d'éclipses à chaque saison d'éclipses-3
Au plus trois éclipses (Lune et Soleil)
La variation de longitude de la Terre par rapport à la ligne des noeuds durant une lunaison étant de 30,67° et l'arc BB' ayant une longueur de 31,33°, il est également possible d'avoir deux conjonctions contenues dans l'arc BB'. Dans ce cas les conjonctions sont proches des extrémités de l'arc BB' et l'opposition comprise entre ces deux conjonctions est proche du noeud de l'orbite lunaire. De même on peut avoir deux oppositions dans l'arc BB'. Dans ce cas les oppositions sont proches des extrémités de l'arc BB' et la conjonction comprise entre ces deux oppositions se trouve proche du noeud de l'orbite lunaire. De plus comme nous l'avons déjà signalé, les éclipses proches des extrémités de l'arc BB' donc loin du noeud sont des éclipses faibles, donc des éclipses partielles de Soleil ou des éclipses de Lune par la pénombre et les éclipses proches du noeud sont des éclipses fortes, donc des éclipses centrales de Soleil ou des éclipses totales de Lune.
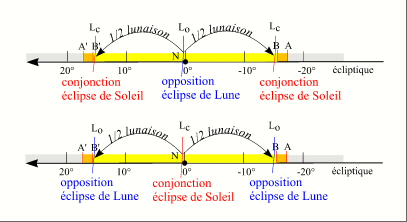
Conjonction et opposition au voisinage du noeud
Crédit : IMCCE/Patrick Rocher
On peut donc avoir une série de trois éclipses, au voisinage du passage de la Terre (ou du soleil apparent) par un noeud de l'orbite lunaire. Dans ce cas, on a soit une éclipse forte de Soleil (éclipse centrale) encadrée par deux éclipses faibles de Lune (éclipses par la pénombre) soit une éclipse forte de Lune (éclipse totale) encadrée par deux éclipses faibles de Soleil (éclipses partielles).
Nombre d'éclipses par an
Une année civile du calendrier grégorien comporte 365 ou 366 jours. La lunaison moyenne est de 29,53 jours, une année lunaire de douze lunaisons a donc 354 jours, l'écart entre les deux années est de 11 ou 12 jours. Durant ces jours, la demi-lunaison étant supérieure à 14 jours, il ne peut pas y avoir à la fois une conjonction et une opposition. Donc une année civile ne peut jamais avoir à la fois 13 conjonctions (nouvelles Lunes) et 13 oppositions (pleines Lunes). Une seule de ces deux conjonctures est possible, dans ce cas la première conjonction ou opposition a lieu dans les 11 (ou 12) premiers jours de janvier et la dernière conjonction ou opposition a lieu dans les 11 (ou 12) derniers jours de décembre. On a donc, au maximum, soit une année civile à 13 oppositions, soit une année civile à 13 conjonctions. La saison des éclipses est égale à 173,31 jours, donc tous les 173 jours, aux conjonctions et oppositions les plus proches de ces dates il y a au moins deux éclipses (une de Soleil et une de Lune) et il y a au plus trois éclipses (deux de Lunes et une de Soleil ou deux de Soleil et une de Lune).
Nombre d'éclipses par an-2
Une année civile peut contenir au maximum deux saisons d'éclipses entières, soit trois passages de la Terre par un des noeuds de l'orbite lunaire, le premier étant en début d'année, le second en milieu d'année et le dernier en fin d'année. À chacun de ces passages, on peut associer un couple ou un triplet d'éclipses. Mais l'on n'a jamais un triplet d'éclipses complet en début et en fin d'année, et dans le cas ou l'on a deux triplets complets à deux passages consécutifs le troisième passage ne comporte qu'une éclipse dans l'année en cours, car s'il présentait deux éclipses dans l'année en cours, il y aurait 13 oppositions et 13 conjonctions dans l'année, chose impossible. Donc dans une année civile, on a au maximum sept éclipses.
Nombre d'éclipses par an-3
Le tableau ci-contre regroupe toutes les combinaisons possibles.
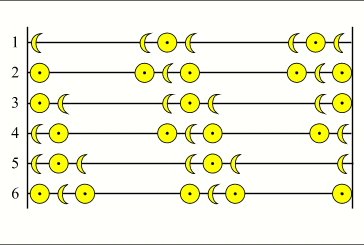
Liste des combinaisons possibles de 7 éclipses dans une année civile
Crédit : IMCCE/Patrick Rocher
On remarque dans ce tableau que les triplets d'éclipses qui se suivent à six lunaisons d'intervalle ont la même composition. En effet, comme on l'a déjà signalé, dans chaque triplet, l'éclipse médiane se produit très près du noeud, or l'éclipse médiane du triplet suivant sera forcément une éclipse du même corps, la conjonction ou l'opposition n'ayant avancé que de 4° environ. De plus lorsque l'on a sept éclipses par an la première et la dernière éclipse sont des éclipses du même corps, la première a toujours lieu dans les 11 (ou 12) premiers jours de janvier et la dernière a toujours lieu dans les 11 (ou 12) derniers jours de décembre.
En conclusion le nombre maximal d'éclipses dans une année civile est de sept éclipses, avec obligatoirement deux éclipses de Soleil et deux éclipses de Lune, pour les trois autres toutes les combinaisons sont possibles. Le nombre minimal d'éclipses dans une année est de quatre, avec obligatoirement deux éclipses de Lune et deux éclipses de Soleil.
Les séries courtes d'éclipses
Nous allons nous intéresser à l'évolution des éclipses au cours du temps. Supposons que nous ayons une éclipse de Soleil à une date donnée comment sera l'éclipse suivante ?
Généralement les éclipses successives de Soleil sont séparées par six lunaisons (liées à une saison d'éclipses), donc il y a alternance de noeud lunaire (noeud ascendant et noeud descendant). Nous avons vu que durant une lunaison la Terre (ou le soleil apparent) progressait en moyenne de 30,67° en longitude par rapport à la ligne des noeuds de l'orbite lunaire, donc au bout de six lunaisons la Terre (ou le Soleil apparent) progresse de 6 x 30,67° = 184,02°, donc si dl1 est la différence de longitude entre la conjonction et le noeud de l'orbite lunaire pour la première éclipse, l'éclipse suivante a lieu au noeud suivant et la différence dl2 entre la conjonction et ce noeud est égale à dl1 - (184,02° - 180°) = dl1- 4,02°. Donc la conjonction se déplace par rapport aux noeuds successifs d'environ 4° dans le sens direct d'une éclipse à la suivante.
Les séries courtes d'éclipses-2
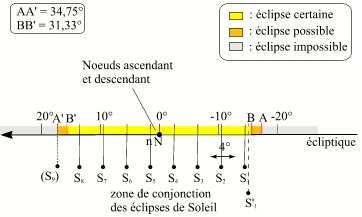
Série courte d'éclipses (vu depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Les éclipses de la suite courte S1 à S8 ont lieu à chaque saison d'éclipse, alternativement au noeud ascendant puis au noeud descendant. Il y a toujours au moins 8 éclipses dans la suite car l'arc BB' contient 7 arcs de 4° donc 8 éclipses. Il peut éventuellement y avoir une neuvième éclipse S9 (dans l'arc A'B'), dans ce cas cette éclipse est la dernière éclipse d'un triplet d'éclipses : Soleil-Lune-Soleil. Dans ce cas la conjonction correspondant à la première éclipse du triplet a lieu une lunaison plus tôt et se trouve 30,67° en amont et cette éclipse est la première éclipse de la série courte suivante; nous avons donc un décrochage dans la suite des séries, la série suivante commence avant que la série en cours ne soit terminée. Ce phénomène peut également se produire lorsque la huitième éclipse de la série est très proche du point B'. On peut donc conclure que les éclipses des suites courtes sont séparées par six lunaisons et que la première éclipse d'une suite courte est séparée de la dernière éclipse de suite courte précédente par cinq lunaisons ou par une lunaison dans le cas d'un décrochage.
Les séries courtes d'éclipses-3
On remarque que les conjonctions liées aux éclipses d'une série courte parcourent l'arc BB' dans le sens direct avec un pas moyen de 4°, les premières et les dernières éclipses sont des éclipses faibles (éclipses partielles ou éclipses centrales de faible magnitude) et les éclipses du milieu de la série, proches des noeuds, sont des éclipses fortes (éclipses centrales). On rappelle que les types des éclipses centrales : annulaire, totale ou mixte ne dépendent pas de la distance entre la conjonction et le noeud mais des diamètres apparents des corps liés aux positions orbitales de la Lune et du Soleil.
Attention, il ne faut jamais oublier que ces calculs sont faits à l'aide des révolutions moyennes de la Lune, la réalité est toujours un peu différente, l'avance de la conjonction n'est donc jamais exactement égale à 4° mais varie autour de cette valeur moyenne.
Répartition des éclipses sur une période de 22 ans
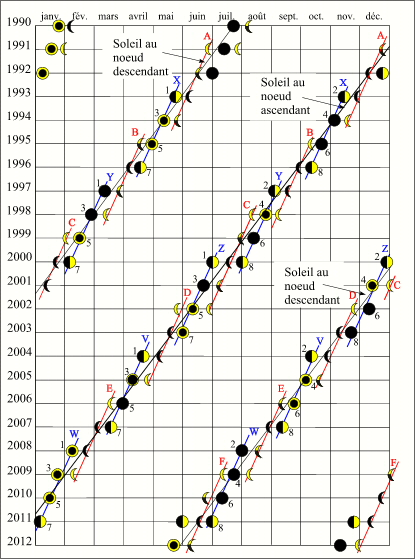
Éclipses de Lune et de Soleil entre 1990 et 2012.
Crédit : IMCCE/Patrick Rocher
Sur le diagramme ci-contre, nous avons fait figurer l'ensemble des éclipses de Lune et de Soleil comprises entre l'an 1990 et l'an 2012. Les éclipses sur ce diagramme sont représentées de la manière suivante :

Crédit : IMCCE/Patrick Rocher
On remarque que les éclipses ont bien lieu aux voisinages des passages du Soleil dans la direction des noeuds ascendant et descendant de l'orbite lunaire. De même on constate qu'à chaque saison d'éclipse on a un doublet d'éclipses Lune-Soleil ou un triplet d'éclipses Lune-Soleil-Lune (1991) ou Soleil-Lune-Soleil (2000) et que dans le cas des triplets les éclipses en première et dernière positions sont faibles et que l'éclipse médiane est forte. On observe que les éclipses de Soleil ou de Lune de début et de fin de séries courtes sont séparées par cinq ou une lunaisons. On vérifie également qu'il y a toujours au moins quatre éclipses par an, sur la période de temps représentée, il n'y a pas d'année à 7 éclipses, mais une année à 6 éclipses (2000).
La démonstration de l'existence des séries courtes de Soleil est également valable pour des séries courtes d'éclipses de Lune. Il suffit de remplacer la conjonction par l'opposition. Sur notre diagramme nous avons fait figurer les séries courtes de Soleil (en bleu) et les séries courtes de Lune (en rouge). On constate que les traits joignant les éclipses d'une même série pour chaque noeud sont parallèles et coupent les lignes des noeuds. Sur la période considérée, il n'y a pas de série courte à 9 éclipses. Mais on peut observer plusieurs décrochage de séries courtes, par exemple la série courte de Soleil Z débute avant que la série Y soit terminée (triplet d'éclipses de l'an 2000).
exercice eclipse soleil
Canons et grandeurs des éclipses de Soleil
Introduction
 Introduction
Introduction
Nous étudions maintenant les éclipses de Soleil sur de très grandes période de temps, pour cela nous construisons des canons d'éclipses.
Les parties pour en savoir plus vous donnent les caractéristiques du canon d'éclipses construit à l'IMCCE, ainsi que les listes des éclipses totales et annulaires les plus longues et des éclipses partielles les plus courtes avec des détails et des commentaires.
Les canons d'éclipses de Soleil
Les listes d'éclipses de Lune et de Soleil sont publiées dans des livres appelés canons d'éclipses. Le plus connu est celui de Theodor Ritter von Oppolzer, sa première édition date de 1887 dans le volume 52 des Mémoires de Mathématiques et de Sciences Naturelles de l'Académie Impériale de Vienne. Ce canon, corrigé, est réédité régulièrement. Dans ce canon, on trouve 8000 éclipses de Soleil comprises entre -1207 et 2161 et 5200 éclipses de Lune comprises entre -1206 et 2132. Il faut préciser que l'on n'y trouve pas les éclipses de Lune par la pénombre.
Il convient de citer également le canon des éclipses de Soleil de Jean Meeus et Hermann Mucke (1983, Astronomisches Büro, Vienne), contenant toutes les éclipses de Soleil comprises entre -2003 et 2526.
À l'IMCCE, nous avons construit un canon d'éclipses de Lune et de Soleil. Il porte sur une période de 6000 ans (de l'an -2999 à 3000), il a été construit avec les dernières théories planétaires et lunaire élaborées à l'IMCCE.
Ces trois canons ont été construits avec des théories différentes des corps célestes et avec des constantes légèrement différentes, cela implique que certaines éclipses limites ne sont pas identiques (apparition de nouvelles éclipses limites, ou éclipses totales dans un canon qui deviennent mixtes dans l'autre).
En savoir plus: Le canon de l'IMCCE : les théories utilisées
 En savoir plus
En savoir plus
Pour construire notre canon nous avons utilisé les théories suivantes :
- Théorie de la Lune : ELP2000 de Michèle Chapront-Touzé et J. Chapront.
- Théorie du barycentre Terre-Lune : VSOP82 de P. Bretagnon.
- Éphémérides sous forme de polynômes de Tchebycheff : SLP98 de G. Francou
- TT-TU : valeurs de R. Stephenson (1984) modifiées et adaptées à la théorie de la Lune utilisée.
- Théorie de la précession de Lieske (1977).
- Théorie de la nutation de Wahr (1981).
- Temps sidéral d'Aoki (1992)
En savoir plus: Le canon de l'IMCCE : les paramètres physiques
 En savoir plus
En savoir plus
Les paramètres physiques utilisés sont les suivants :
- le demi-diamètre solaire = 15' 59.63"
- le rapport du rayon lunaire sur le rayon équatorial terrestre : k = 0,2725076
- le rayon équatorial terrestre = 6 378 140 m
- le carré de l'ellipticité de l'ellipsoïde terrestre = 0,00669438 -- 1/f = 1/298.257 IERS (1992)
En savoir plus: Le canon de l'IMCCE : les résultats
 En savoir plus
En savoir plus
Nous avons trouvé sur cette période de 6000 ans, 14 155 éclipses de Soleil qui se répartissent de la manière suivante :
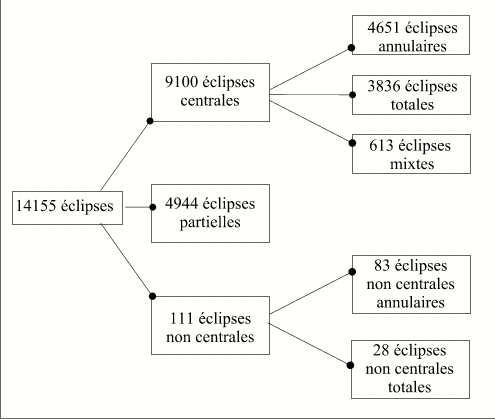
Crédit : IMCCE/Patrick Rocher
Comme on l'a prédit précédemment, on constate qu'il y a bien plus d'éclipses annulaires que d'éclipses totales.
Les éclipses totales les plus longues
Une éclipse totale a une durée maximale lorsque l'ombre est la plus grande possible, c'est-à-dire lorsque la Terre est à l'aphélie pour avoir le plus petit diamètre apparent du Soleil, lorsque la Lune est au périgée pour avoir le plus gros diamètre apparent de la Lune et lorsque le maximum a lieu au zénith du lieu d'observation pour avoir une distance observateur Lune minimale, donc un diamètre de l'ombre maximal. La première condition fixe la date de l'éclipse (actuellement début juillet). La troisième condition fixe le lieu d'observation proche du tropique du Cancer (latitude 23°). Avec la Lune au périgée, la vitesse synodique de l'ombre par rapport à la Terre est de 3 733 km/h (1 037 m/s) et la vitesse de l'ombre sur la surface de la Terre est de 2 196 km/h (610 m/s), le diamètre de l'ombre est alors de 262 km et la durée de l'éclipse est de 7 min 10 s. En réalité, ces paramètres ne sont pas indépendants et l'on s'aperçoit, en faisant un calcul plus rigoureux, que si l'on descend en latitude vers +5° la durée de l'éclipse croît jusqu'à environ 7 min 30 s. En effet le diamètre de l'ombre va décroître (on n'est plus au zénith, l'ombre devient ovale) mais sa vitesse décroît encore plus rapidement ce qui en fin de compte augmente sensiblement la durée de l'éclipse. Le tableau suivant porte sur l'ensemble des éclipses totales comprises entre l'an -2999 et 3000 issues du canon d'éclipses de Soleil de l'IMCCE.
Les éclipses totales les plus longues-2
| Date |
Durée |
Date |
Durée |
Date |
Durée |
| 29 mai -2584 |
7 min 17,00 s |
10 juin - 2566 |
7 min 23,76 s |
20 juin - 2548 |
7 min 19,94 s |
| 25 avril - 2266 |
7 min 10,49 s |
05 avril - 2248 |
7 min 23,37 s |
16 avril - 2230 |
7 min 27,25 s |
| 27 mai -2212 |
7 min 21,11 s |
8 juin - 1106 |
7 min 10,61 s |
24 mai - 779 |
7 min 13,45 s |
| 05 juin - 761 |
7 min 28,61 s |
15 juin - 743 |
7 min 31,73 s |
26 juin -725 |
7 min 23,45 s |
| 11 mai - 425 |
7 min 16,51 s |
22 mai - 407 |
7 min 18,11 s |
02 juin - 389 |
7 min 10,01 s |
| 22 mai 114 |
7 min 10,41 s |
01 juin 132 |
7 min 19,50 s |
12 juin 150 |
7 min 17,99 s |
| 16 juin 345 |
7 min 21,13 s |
27 juin 363 |
7 min 28,42 s |
08 juillet 381 |
7 min 26,87 s |
| 19 juillet 399 |
7 min 15,75 s |
23 mai 681 |
7 min 14,32 s |
03 juin 699 |
7 min 21,62 s |
| 13 juin 717 |
7 min 20,47 s |
29 mai 1044 |
7 min 16,79 s |
09 juillet 1062 |
7 min 25,27 s |
| 20 juin 1080 |
7 min 22,83 s |
01 juillet 1098 |
7 min 10,21 s |
20 juin 1955 |
7 min 12,62 s |
| 25 juin 2150 |
7 min 18,77 s |
05 juillet 2168 |
7 min 30,89 s |
16 juillet 2186 |
7 min 34,14 s |
| 27 juillet 2204 |
7 min 26,93 s |
08 août 2222 |
7 min 10,39 s |
14 juin 2504 |
7 min 15,03s |
| 25 juin 2522 |
7 min 17,54 s |
23 juin 2867 |
7 min 14,67 s |
03 juillet 2885 |
7 min 15,80 s |
Liste des éclipses totales d'une durée supérieure à 7 minutes et 10 secondes
On constate que l'éclipse la plus longue sera celle du 16 juillet 2186 pour une durée de 7 min 34,14 s, valeur légèrement supérieure à celle calculée avec les valeurs moyennes.
Les éclipses annulaires les plus longues
Dans le cas d'une éclipse annulaire le raisonnement est similaire aux éclipses totales, mais inverse. Le diamètre apparent du Soleil doit être le plus grand possible donc la Terre doit être au périhélie et le diamètre apparent de la Lune doit être le plus petit possible donc la Lune doit être à l'apogée, dans ce cas la durée maximale de l'éclipse peut atteindre 12 min 30 s. Le tableau suivant porte sur l'ensemble des éclipses annulaires comprises entre l'an -2999 et 3000 issues du canon d'éclipses de Soleil de l'IMCCE .
| Date |
Durée |
Date |
Durée
|
| 12 décembre -1655 |
11 min 53,93 s |
10 décembre - 195 |
11 min 57,93 s |
| 22 décembre - 177 |
12 min 01,43 s |
25 novembre 132 |
12 min 08.01 s |
| 06 décembre 150 |
12 min 15,91 s |
17 décembre 168 |
12 min 07.25 s |
| 25 décembre 1628 |
11 min 55,47 s |
02 décembre 1937 |
11 min 53.63 s |
| 14 décembre 1955 |
12 min 02,49 s |
24 décembre 1973 |
11 min 55.75 s |
Liste des éclipses annulaires d'une durée supérieure à 11 minutes et 50 secondes
Les éclipses partielles les plus petites
À l'aide du canon d'éclipses de Soleil de l'IMCCE nous avons cherché quelles sont les éclipses partielles les plus petites sur la période -2999, 3000. Nous avons trouvé les deux éclipses suivantes :
| Date |
Magnitude |
Instant du maximum |
Durée générale |
| 23 juillet 651 |
0,0008272 |
08h 30 m 41,06 s UT |
9,3 min |
| 17 août 1327 |
0,0004937 |
16 h 58 m 33,03 s UT |
6,2 min |
Nous allons étudier ces deux éclipses.
L'éclipse de 651
Éphémérides de la Lune au voisinage de l'éclipse :
- le 15/07/0651 à 07h 31m 28s UT : Dernier Quartier.
- le 22/07/0651 à 01h 25m 11s UT : la Lune passe par le noeud descendant de son orbite.
- le 22/07/0651 à 14h 50m 11s UT : la Lune à l'apogée, d=406450 km, diam. app. =29,5'.
- le 23/07/0651 à 08h 30m 41s UT : maximum de l'éclipse.
- le 23/07/0651 à 08h 47m 30s UT : Nouvelle Lune.
On constate que cette éclipse a lieu après le passage au noeud descendant de l'orbite lunaire, comme l'éclipse est très faible le passage au noeud doit être loin de la conjonction et l'instant du maximum de l'éclipse loin de l'instant de la conjonction. C'est effectivement le cas, on a un écart de temps égal à 16m 49s entre la conjonction et le maximum de l'éclipse et on a également un écart de temps maximal égal à 31h 22m 19s entre la conjonction et le passage au noeud. Ces valeurs sont presque des valeurs extrêmes car la Lune est voisine de son apogée et la Terre est proche de son aphélie, donc la Lune et le Soleil se déplacent lentement. On remarque que comme nous l'avons expliqué précédemment le maximum de l'éclipse (distance minimale entre le centre de la Lune et le centre du Soleil) a bien lieu entre le passage au noeud et la conjonction.
L'éclipse de 1327
Éphémérides de la Lune au voisinage de l'éclipse :
- le 14/08/1327 à 15h 01m 55s UT : la Lune au périgée d=365783 km, diam. app. =32,7'.
- le 17/08/1327 à 16h 43m 04s UT : Nouvelle Lune.
- le 17/08/1327 à 16h 58m 33s UT : maximum de l'éclipse.
- le 18/08/1327 à 21h 34m 46s UT : la Lune passe par le noeud ascendant de son orbite.
- le 25/08/1327 à 06h 20m 50s UT : Premier Quartier.
- le 26/08/1327 à 12h 15m 12s UT : la Lune à l'apogée d=404381 km, diam. app. =29,6'.
Cette éclipse a lieu avant le passage au noeud ascendant, on a donc le scénario suivant, conjonction, maximum de l'éclipse et passage au noeud. L'écart de temps entre la conjonction et le maximum de l'éclipse est de 15m 29s et l'écart de temps entre la conjonction et le passage au noeud est de 28h 36m 13s.
Pour ces deux éclipses, qui sont des cas extrêmes, on voit que le maximum de l'éclipse est relativement proche de la conjonction, par contre la conjonction est très éloignée du passage au noeud (plus d'une journée).
Les éclipses récentes et futures
Introduction
 Introduction
Introduction
Cette section comporte des cartes représentant les lignes de centralité des éclipses (totales, annulaires et mixtes).
On donne lrs cartes des éclipses centrales sur la période 1998 à 2020, les cartes des éclipses visibles en France depuis le XVIe siècle jusqu'à la fin du XXIe siècle. Des tableaux donnent les zones de visibilité sur le pays.
Les éclipses totale entre 1998 et 2020
La carte ci-contre donne les bandes de totalité des éclipses totales de Soleil entre l'an 1998 et l'an 2020. On remarquera la très grande dispersion des courbes à la surface terrestre. On notera la largeur des bandes de totalité des éclipses proches des pôles et l'étroitesse de la bande de totalité de l'éclipse mixte.
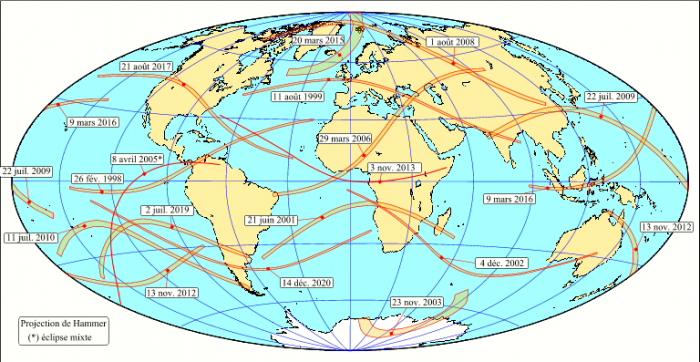
Crédit : IMCCE/Patrick Rocher
Les éclipses annulaires entre 1998 et 2020
La carte ci-contre donne les bandes de centralité des éclipses annulaires de Soleil entre l'an 1998 et l'an 2020. On remarquera la très grande dispersion des courbes à la surface terrestre.
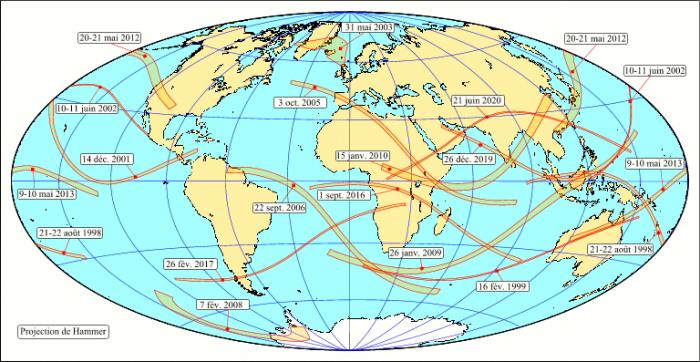
Crédit : IMCCE/Patrick Rocher
Fréquence des éclipses centrales de Soleil en France
Vu la faible surface traversée par la bande de centralité, les éclipses visibles sur un territoire ayant la superficie de la France sont peu nombreuses et si on se limite à une ville où une région, elles deviennent exceptionnelles.
Les tableaux suivants donnent la liste des éclipses dont la bande de centralité traverse la France, il porte sur toutes les éclipses centrales allant du début du XVIe siècle jusqu'à la fin du XXIe siècle.
| Date |
Type d'éclipses |
Remarques |
| 24 janvier 1544 |
totale* |
visible dans le sud-est de la France |
| 12 octobre 1605 |
totale |
visible dans le sud ouest de la France |
| 10 juin 1630 |
totale* |
la fin de l'éclipse est visible de l'ouest au sud-est de la France |
| 27 janvier 1683 |
annulaire |
la fin de l'éclipse est visible à l'ouest et au centre de la France |
| 12 mai 1706 |
totale |
visible dans le sud-est de la France |
| 22 mai 1724 |
totale |
visible du nord-ouest au nord-est de la France , visible à Paris |
| 1 avril 1764 |
annulaire |
visible dans le nord de la France, visible à Paris |
| 7 septembre 1820 |
annulaire |
visible dans le nord-est de la France, invisible à Paris |
| 8 juillet 1842 |
totale |
visible dans le sud-est de la France |
| 9 octobre 1847 |
annulaire |
visible du nord-est au centre-est de la France |
(*) Ces deux éclipses sont données comme mixtes dans le canon de Meeus et comme totales dans le canon d'Oppolzer.
Fréquence des éclipses centrales de Soleil en France-2
| Date |
Type d'éclipse |
Remarques |
| 17 avril 1912 |
mixte |
visible de l'ouest au nord-est de la France, visible au nord de Paris (éclipse perlée) |
| 15 février 1961 |
totale |
visible dans le sud de la France |
| 11 août 1999 |
totale |
visible dans le nord de la France d'ouest en est |
| 5 novembre 2059 |
annulaire |
visible dans le sud-ouest de la France |
| 13 juillet 2075 |
annulaire |
visible en Corse et dans l'extrême sud-est de la France |
| 3 septembre 2081 |
totale |
visible dans le centre de la France |
| 27 février 2082 |
annulaire |
visible dans le sud de la France |
| 23 septembre 2090 |
totale |
fin de l'éclipse visible dans le nord-ouest de la France |
 Remarque
Remarque
Quelques auteurs citent, à tort, l'éclipse du 12 août 2026 comme visible en France. Camille Flammarion la donne visible à Paris (1880, L'Astronomie Populaire). Paul Couderc la dit visible sur une ligne allant de Bordeaux à Toulouse (1971, Les éclipses). En réalité, la phase de totalité de cette éclipse ne sera pas visible en France mais au nord de l'Espagne.
Eclipses du XVI, XVII et XVIIIème siècles, visibles en France
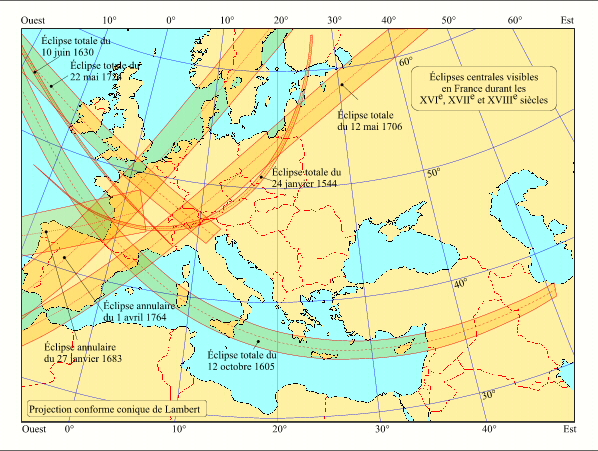
Crédit : IMCCE/Patrick Rocher
La carte ci-contre donne les lignes de centralité des éclipses centrales (totales, annulaires ou mixtes) visibles en France. On notera la grande diversité de largeur des bandes de centralité.
Eclipses du XIX et du XXème siècles visibles en France
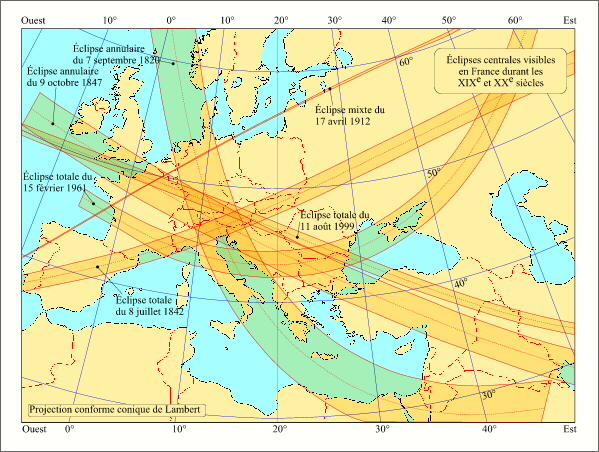
Crédit : IMCCE/Patrick Rocher
La carte ci-contre donne les lignes de centralité des éclipses centrales (totales, annulaires ou mixtes) visibles en France. L'éclipse de 1912 est une éclipse mixte, elle a été observée au nord de Paris (Saint-Germain en Laye), on notera l'étroitesse de sa ligne de centralité. On notera également que les trajectoires des lignes de centralité présentent des orientations très variées par rapport aux méridiens et aux parallèles terrestres et qu'elles sont loin d'être parallèles à l'équateur terrestre.
Eclipses du XXI siècle visibles en France
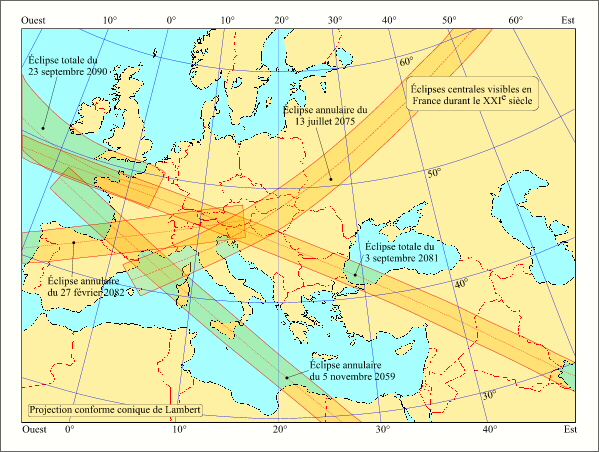
Crédit : IMCCE/Patrick Rocher
La carte ci-contre donne les lignes de centralité des éclipses centrales (totales et annulaires) visibles sur la France.
Observation d'une éclipse de Soleil
Introduction
 Introduction
Introduction
Cette section est très importante car elle traite des dangers liés à l'observation directe du Soleil. Donc des dangers liés à l'observation d'une phase non totale d'une éclipse.
Précautions à prendre pour observer une éclipse de Soleil
Si on décompose la lumière solaire à l'aide d'un prisme, on aperçoit une série de couleurs allant du violet au rouge. Ces couleurs forment le spectre visible de la lumière solaire. Leurs longueurs d'onde varient de 400 nm (1 nanomètre = 1 millionième de millimètre) pour le violet à 750 nm pour le rouge. Le spectre de la lumière solaire ne se limite pas aux couleurs visibles, mais s'étend dans les basses longueurs d'onde avec les ultraviolets et les rayons X, et vers les grandes longueurs d'onde avec l'infrarouge et les ondes radio. Les rayonnements ultraviolets ont une longueur d'onde comprise entre 15 nm (Rayon X) et 400 nm (lumière visible violet).
On classe le rayonnement ultraviolet en plusieurs catégories :
- les UV C, entre 200 nm et 280 nm, très dangereux, mais ils sont filtrés par l'atmosphère terrestre,
- les UV B, entre 280 nm et 315 nm, qui peuvent engendrer des lésions très graves,
- les UV A, entre 315 nm et 380 nm, qui sont à l'origine du bronzage de la peau et de la photosynthèse de la vitamine D.
Ces rayonnements sont tous nocifs pour la vue, d'où l'usage de lunettes de soleil de bonne qualité pour les journées ensoleillées.
Précautions à prendre pour observer une éclipse de Soleil-2
Les rayonnements infrarouges ont une longueur d'onde comprise entre 800 nm (lumière visible rouge) et 1 mm (ondes radio). Ces rayonnements sont détectés par la chaleur à laquelle ils sont associés.
La concentration du rayonnement solaire permet d'atteindre des températures très élevées. Ainsi, il est très facile d'enflammer une feuille de papier à l'aide d'une loupe et d'un rayon de soleil.
Iriez-vous mettre votre oeil à la place de ce petit bout de papier ? Non ! Alors ne mettez jamais votre oeil derrière un instrument d'optique (lunette, jumelles, appareil photo) qui focalise la lumière solaire et qui n'est pas équipé d'un filtre spécialement conçu pour l'observation solaire.
De même, il est fortement déconseillé de regarder le Soleil à l'oeil nu, même avec des lunettes de soleil. En effet ces lunettes, si elles sont de bonne qualité, protègent du rayonnement ultraviolet mais ne sont nullement conçues pour regarder le Soleil de face car elles n'arrêtent pas le rayonnement infrarouge. On estime, que même lorsque le disque solaire est éclipsé à 99%, le rayonnement solaire peut causer des dommages irréversibles et au moment où vous êtes ébloui il est déjà trop tard.
Précautions à prendre pour observer une éclipse de Soleil-3
Le seul moment, très court, où l'on peut regarder sans danger directement le Soleil durant une éclipse est la phase de totalité.
Mais attention la douleur que l'on ressent en regardant le Soleil en face provient de la pupille qui veut se fermer plus qu'elle ne le peut, c'est cette douleur qui nous fait détourner le regard. Mais un mauvais filtre peut supprimer cette douleur, et laisse passer le rayonnement infrarouge qui va brûler la rétine d'une manière indolore, le fond de l'oeil n'est pas sensible à la douleur et toute brûlure est irréversible.
Il convient donc de prendre énormément de précautions pour observer une éclipse de Soleil.
Une méthode classique consiste à observer le phénomène par projection. Pour cela munissez-vous de deux feuilles de papier cartonné. La première, percée d'un minuscule trou, est positionnée perpendiculairement à la direction du soleil, la deuxième est placée parallèlement à la première ; lorsque cette seconde feuille est suffisamment éloignée de la première (environ un demi-mètre), on peut y observer l'image du soleil. On peut également observer l'éclipse par projection avec un instrument d'optique, par exemple une petite lunette. Pour cela, il suffit d'orienter la lunette vers le Soleil, sans utiliser le chercheur de l'instrument, mais en orientant la lunette de manière à minimiser la dimension de son ombre. La première méthode est absolument sans danger, la deuxième présente le risque de voir une personne distraite ou non informée (souvent des enfants), mettre son oeil derrière l'instrument.
L'utilisation de filtres pour l'observation des éclipses
Les filtres solaires
Il existe de nombreux types de filtres solaires, utilisés par les astronomes professionnels et amateurs pour l'observation du Soleil. Ces filtres ont deux objectifs, réduire l'intensité lumineuse et filtrer les rayonnements ultraviolets et infrarouges. Ces filtres possèdent une fine couche d'aluminium, de chrome ou d'argent sur leur surface. C'est cette couche métallique qui filtre le rayonnement infrarouge. Ces filtres, pour être efficaces, doivent être montés devant les systèmes optiques (devant la lunette où le télescope), cela explique à la fois leur grand diamètre et leur prix souvent élevé. On trouve parfois, vendus avec des lunettes astronomiques du commerce, des filtres solaires qui se placent sur l'oculaire ; ces filtres sont dangereux, en effet, la lumière solaire traverse alors tout le système optique, ce qui concentre le rayonnement ultraviolet et peut briser le filtre par échauffement. On peut utiliser un filtre solaire vissé sur l'oculaire, uniquement s'il est associé avec un hélioscope d'Herschel. Si vous possédez un instrument d'observation consultez votre revendeur qui pourra vous conseiller pour l'achat d'un filtre solaire adapté à votre instrument.
L'utilisation de filtres pour l'observation des éclipses-2
Si vous ne voulez pas investir trop d'argent dans l'achat d'un filtre solaire, vous pouvez confectionner un filtre en Mylar.
Le Mylar se présente sous la forme d'une mince feuille métallique aluminée. Son pouvoir filtrant est très performant, il filtre parfaitement les rayonnements infrarouge et UV et diminue l'intensité lumineuse d'un facteur 1 000 000. Son seul défaut est sa fragilité, due à sa faible épaisseur. Il faut également se méfier d'un éventuel défaut de surface. Utilisez toujours des feuilles parfaitement planes (n'ayant subi aucun pli). Ces feuilles sont faciles à découper et peuvent donc être utilisées pour la création du filtre de votre choix. Vous pouvez en équiper une paire de lunettes. Ainsi, La revue Ciel et Espace en association avec l'ASNAV (Association Nationale pour l'Amélioration de la Vue) a distribué une paire de lunette munie de filtre en Mylar dans son numéro d'octobre 1996, pour l'observation de l'éclipse du 12 octobre 1996. De telles lunettes permettent d'observer les éclipses à " l'oeil nu ", mais, elles ne doivent pas être utilisées pour regarder à travers un instrument. De plus elles ne doivent pas être utilisées après leur date limite d'utilisation.
Le filtre, quel qu'il soit, doit toujours être placé devant l'instrument et non entre l'instrument et l'observateur.
L'utilisation de filtres pour l'observation des éclipses-3
Liste des filtres pouvant être utilisés pour observer une éclipse de Soleil
- filtres solaires spéciaux.
- filtres en Mylar.
- plaques de verre d'indice maximal pour les masques de soudeur.
- plusieurs épaisseurs de négatifs noir et blanc totalement opaques, complètement développés et contenant une émulsion argentine (attention les films négatifs couleurs et certains films négatifs noir et blanc n'en contiennent pas).
Nous vous conseillons vivement les deux premiers, les autres, tenant plus du bricolage, ne sont pas sans risques.
En cas de doute n'hésitez pas à consulter une personne compétente, c'est-à-dire un ophtalmologiste, ou observez l'éclipse par projection.
L'utilisation de filtres pour l'observation des éclipses-4
Liste non exhaustive des filtres À NE PAS utiliser
- Les morceaux de verre noirci à la flamme d'une bougie.
- Les filtres photographiques en gélatine.
- Les filtres polarisants, croisés ou non.
- Les plaques rayons X exposées.
- Les négatifs couleurs ou les négatifs noir et blanc ne contenant pas d'émulsion argentine.
- Une ou plusieurs paires de lunettes.
Les traumatismes causés par le Soleil
Si vous regardez sans précaution une éclipse de Soleil, vous risquez une brûlure grave du fond de l'oeil. Au moment de la brûlure, ce traumatisme est le plus souvent indolore (d'où son danger). Il peut entraîner des cécités définitives ou partielles. Lors de la dernière éclipse visible aux États-Unis, on a dénombré plus de 1 000 cas de cécité définitive et plus de 10 000 cas de cécité temporaire. Même dans les cas de cécité temporaire le traumatise est très long à se résorber (cela peut prendre de 6 mois à un an) et il reste toujours des séquelles. Contrairement à ce que l'on pourrait penser le fait de porter des lunettes de Soleil augmente l'intensité de la brûlure, en effet l'intensité lumineuse étant filtrée par les lunettes, la pupille de l'oeil se dilate et la quantité de lumière infrarouge qui pénètre dans l'oeil est plus importante, d'où une brûlure encore plus intense.
Réponses aux QCM
pages_nombre-eclipses-soleil/stlp-exercice-02-eclipsesol.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 5)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 1)
- Question 5
Solution : réponse 2)
- Question 6
Solution : réponse 2)
 Introduction
Introduction Prérequis
Prérequis



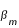 = 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à
= 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à  = 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
= 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).

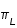 .
.
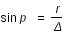 ,
, 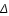 étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.

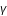 : l' angle S0M0S.
: l' angle S0M0S.
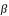 : la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
: la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
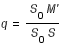 soit
soit 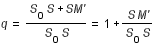
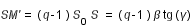 avec
avec 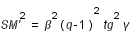
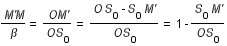
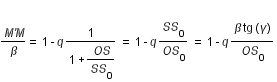
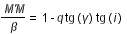
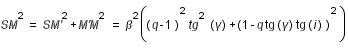 (1)
(1)
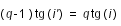
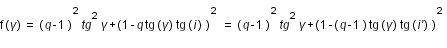
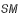 est minimum lorsque
est minimum lorsque 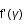 la dérivée de f est nulle
la dérivée de f est nulle
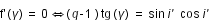 (2)
(2)
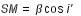 (3)
(3)
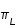 et
et 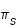 de la Lune et du Soleil.
de la Lune et du Soleil.
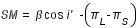 (4)
(4)
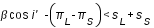
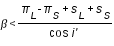 (5)
(5)
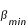 du second membre de (5) est obtenue avec
du second membre de (5) est obtenue avec 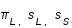 minimales et
minimales et 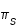 maximale, la valeur supérieure
maximale, la valeur supérieure 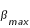 est obtenue avec
est obtenue avec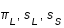 maximales et
maximales et 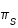 minimale.
minimale.
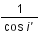
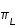
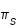
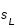
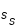
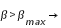 pas éclipse
pas éclipse
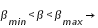 éclipse possible
éclipse possible
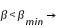 éclipse certaine
éclipse certaine
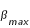 = 1° 34' 45,69" et
= 1° 34' 45,69" et 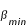 =1° 24' 37,31" et une valeur moyenne
=1° 24' 37,31" et une valeur moyenne 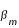 = 1° 28' 51" soit environ 1,48°.
= 1° 28' 51" soit environ 1,48°.
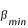 = 0° 52' 55,47" (soit environ 0,88°) et
= 0° 52' 55,47" (soit environ 0,88°) et 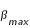 = 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne
= 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne 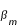 = 0° 56' 42,84" (environ 0,95°).
= 0° 56' 42,84" (environ 0,95°).














