 Introduction
Introduction
Dans cette section nous définissons la ligne des noeuds de l'orbite lunaire et nous étudions son déplacement angulaire moyen dans le plan de l'écliptique. Puis, nous définissons la fréquence avec laquelle le Soleil apparent passe dans la direction de la ligne des noeuds (la saison des éclipses).
Nous définissons ensuite un critère portant sur la latitude de la Lune au moment de sa conjonction avec le Soleil, pour savoir s'il y a ou non une éclipse de Soleil. Nous donnons les bornes de ce critère en fonction du type d'éclipse observable.
Enfin nous transposons ce critère sur la latitude lunaire en un critère sur la différence de longitude entre la longitude de la conjonction et la longitude du noeud lunaire.
Les parties pour en savoir plus vous montre comment calculer la valeur moyenne de la saison d'éclipse, puis nous explique le mouvement réelle de cette ligne. Nous donnons également la démonstration des critères en latitude.
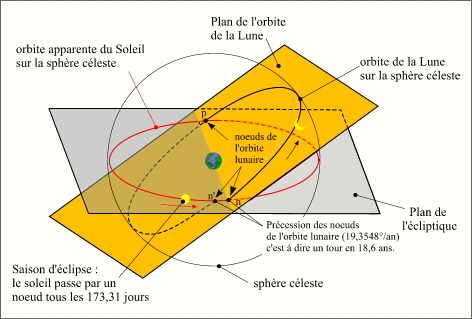
Orbite de la Lune, mouvement de la ligne des noeuds.
Crédit : IMCCE/Patrick Rocher
Il y a éclipse de Soleil lorsque la Terre passe dans le cône d'ombre ou dans le cône de pénombre de la Lune. Le Soleil, la Lune et la Terre sont alors presque alignés, et on est au voisinage de la nouvelle Lune (conjonction). Si le plan de l'orbite de la Lune était le même que le plan de l'orbite de la Terre (écliptique), il y aurait une éclipse de Soleil à chaque nouvelle Lune, or le plan de l'orbite de la Lune est incliné d'environ 5° 17' sur le plan de l'orbite terrestre à la nouvelle Lune. À chaque instant, l'intersection de ces deux plans est une droite appelée ligne des noeuds et les intersections de cette droite avec l'orbite de la Lune sont appelées noeuds de l'orbite lunaire.
Cette ligne des noeuds n'est pas fixe, elle est animée, dans le sens rétrograde (sens des aiguilles d'une montre), d'un mouvement de précession d'une période de 18,6 ans, soit un déplacement moyen de 19,354 8° par an.
Pour qu'il y ait une éclipse il faut donc, dans le repère écliptique géocentrique, que la direction Terre-Soleil soit près de la ligne des noeuds lunaires au moment de la nouvelle Lune. Compte tenu du mouvement moyen de précession des noeuds, le Soleil apparent passe en moyenne par l'un des deux noeuds tous les 173,31 jours. Cette période porte le nom de saison des éclipses. Il passe par le même noeud tous les 346,62 jours, cette période porte le nom d'année des éclipses.
 En savoir plus
En savoir plus
La direction Terre-Soleil est la direction du Soleil apparent vu depuis la Terre, elle fait donc 360° pendant une révolution sidérale de la Terre. La ligne des noeuds de l'orbite lunaire se déplace en moyenne de 19,3413618°/an dans le sens rétrograde. On a donc deux mouvements en sens contraire. La période T qui ramène le Soleil apparent dans la direction d'un même noeud de l'orbite lunaire est solution de l'équation suivante :
T . 360°/an + T . 19,3413618°/an = 360°
ce qui donne T = 360/(360 + 19,3413618) an = 0,9490133 an.
L'année sidérale étant égale à : an = 365,2563632 jours, T = 346,63 jours.
La saison des éclipses correspond à l'intervalle de temps mis par le Soleil apparent pour passer d'un noeud de l'orbite lunaire à l'autre, elle est donc égale à T/2 ~ 173,31 jours.
La valeur de cette période T nous permet de calculer la vitesse moyenne du Soleil apparent (ou de la Terre) dans un repère tournant lié à la ligne des noeuds de l'orbite lunaire. Par rapport à cette ligne des noeuds le Soleil apparent fait un tour de 360° en 346,63 jours, sa vitesse moyenne par rapport à la ligne des noeuds est donc de 360°/346,63j = 1,038°/jour.
 En savoir plus
En savoir plus
En réalité, le mouvement rétrograde de la ligne des noeuds présente des inégalités importantes. À certaines époques, sa vitesse est le double de la moyenne. À d'autres moments, sa vitesse est presque nulle, les noeuds sont alors quasi stationnaires. Cela se produit aux voisinages du passage du Soleil dans la direction de la ligne des noeuds, donc au voisinage des éclipses de Soleil (et aussi de Lune). On peut expliquer ce phénomène de la manière suivante, lorsque le Soleil est sur la ligne des noeuds, il se trouve dans le plan de l'orbite de la Lune, la force perturbatrice du Soleil est alors comprise dans le plan de l'orbite de la Lune, donc la composante perpendiculaire à ce plan est nulle et ne "tire" pas sur le plan de l'orbite. Le fait que les noeuds soient quasi-stationnaires au moment des éclipses est très important, en effet les positions moyennes des noeuds sont alors presque égales aux positions vraies, donc dans l'étude des éclipses on peut utiliser le mouvement moyen des noeuds.
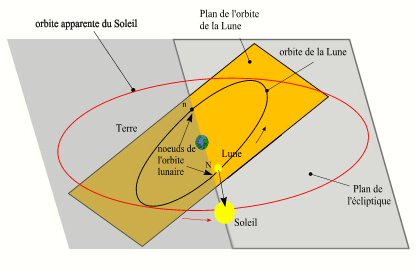
Système Terre - Lune - Soleil lorsque le Soleil est sur la ligne des noeuds
Crédit : IMCCE/Patrick Rocher
On démontre qu'une éclipse de Soleil se produira si, au moment de la nouvelle Lune (instant où les longitudes géocentriques de la Lune et du Soleil sont égales, c'est-à-dire au moment de la conjonction en longitude), la valeur absolue de la différence b des latitudes géocentriques apparentes du centre de la Lune et du centre du Soleil est inférieure à 1,41° (1° 24' 37"), elle se produira peut-être si elle est comprise entre 1,41° (1° 24' 37") et 1,58° (1°34' 46") et elle ne se produira pas si elle est supérieure à 1,58° (1° 34' 46").
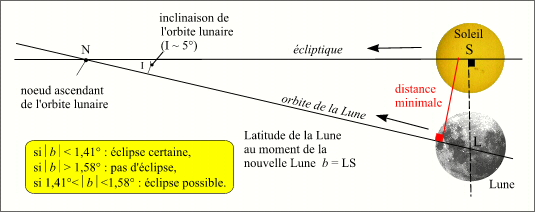
Critères en latitude pour les éclipses de Soleil (vu depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Sur la figure ci-contre, la distance minimale correspond à l'instant où pour un observateur terrestre, le centre de la Lune est le plus près possible du centre du Soleil, cela correspond si l'éclipse a lieu, au maximum de l'éclipse. Durant une éclipse de Soleil on a toujours un des deux scénarii suivants :
- si l'éclipse a lieu avant le passage de la Lune au noeud, on observe d'abord la conjonction (nouvelle Lune), puis le maximum de l'éclipse, puis le passage au noeud,
- si l'éclipse a lieu après le passage de la Lune au noeud, on observe d'abord le passage au noeud, puis le maximum de l'éclipse et enfin la conjonction.
La géométrie de ce dessin montre également que plus la conjonction est proche du noeud, plus la distance minimale entre la Lune et le Soleil est petite et plus la magnitude de l'éclipse est grande. Ainsi, les éclipses partielles correspondent à des conjonctions situées loin des noeuds de l'orbite lunaire et les éclipses centrales (annulaires, totales ou mixtes) correspondent à des conjonctions proches des noeuds de l'orbite lunaire. On rappelle que le fait qu'une éclipse centrale soit annulaire, totale ou mixte ne dépend pas de la distance de la conjonction aux noeuds de l'orbite lunaire, mais dépend uniquement des tailles des diamètres apparents des corps, donc de leurs positions sur leur orbite.
On peut détailler le critère en latitude en déterminant pour quelle valeur de b (0,88°) on a une éclipse centrale avec certitude et pour quelle valeur de b (1,05°) on n'a pas d'éclipse centrale avec certitude (mais une éclipse partielle avec certitude), ces valeurs sont données dans le graphique ci-contre.
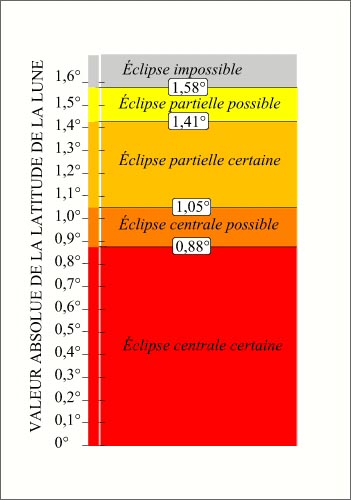
Crédit : IMCCE/Patrick Rocher
On peut également calculer les valeurs moyennes de ces critères en latitude. Pour avoir une éclipse de Soleil il faut que b soit inférieure à 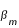 = 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à
= 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à  = 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
= 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
 En savoir plus
En savoir plus
La démonstration du critère en latitude fait intervenir la notion de parallaxe équatoriale solaire et de parallaxe équatoriale lunaire, il convient donc de les définir.
La parallaxe équatoriale solaire est égale à l'angle sous lequel un observateur situé au centre du Soleil voit le rayon terrestre, de même la parallaxe équatoriale lunaire est l'angle sous lequel un observateur situé au centre de la Lune voit le rayon terrestre. C'est également la différence angulaire sous laquelle deux observateurs, l'un situé au centre de la Terre, l'autre situé sur la Terre et observant la Lune à l'horizon, voient le centre de la Lune.
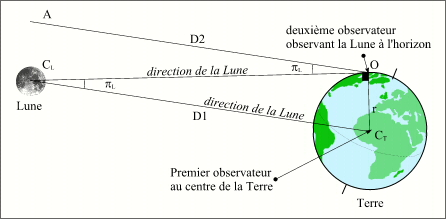
La parallaxe équatoriale lunaire
Crédit : IMCCE/Patrick Rocher
Comme on le constate sur la figure, les deux droites D1 et D2 étant parallèles les angles AOCL et OCLCT sont des angles alternes internes, donc égaux. Ainsi, si les éphémérides donnent une direction angulaire géocentrique de la Lune b, un observateur qui regarde la Lune à l'horizon, la voit dans la direction b -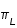 .
.
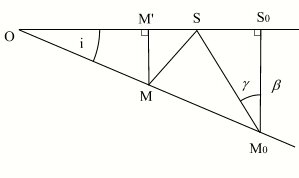
La parallaxe se calcule par la formule : 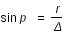 ,
, 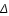 étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
 En savoir plus
En savoir plus
Nous allons établir le critère en latitude dans le cas d'une éclipse au noeud ascendant de l'orbite lunaire, la conjonction ayant lieu avant le passage au noeud. La démonstration est identique pour un passage au noeud descendant ou avec une conjonction située après le passage au noeud, la seule chose qui change dans ce dernier cas est la position du minimum de distance entre des deux corps.
Critère en latitude
Crédit : IMCCE/Patrick Rocher
Soit M0 et S0 : les positions de la Lune et du Soleil à l'instant de la conjonction (nouvelle Lune) avant le passage de la Lune au noeud ascendant de son orbite.
M et S : les positions de la Lune et du Soleil à un instant t postérieur à la conjonction.
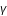 : l' angle S0M0S.
: l' angle S0M0S.
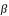 : la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
: la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
q : rapport du mouvement en longitude de la Lune sur celui du Soleil.
Le calcul du critère en latitude consiste à calculer le minimum de la distance SM (corrigé des parallaxes équatoriales lunaire et solaire) et de le comparer avec la somme des demi-diamètres apparents du Soleil et de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore.
 En savoir plus
En savoir plus
On a :
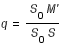 soit
soit 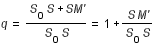
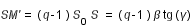 avec
avec 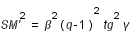
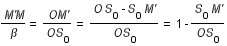
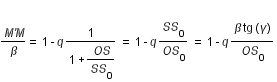
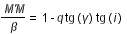
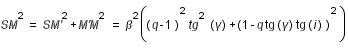 (1)
(1)
On introduit un angle auxiliaire i', tel que : 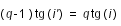
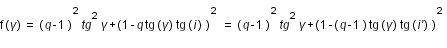
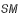 est minimum lorsque
est minimum lorsque 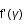 la dérivée de f est nulle
la dérivée de f est nulle
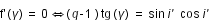 (2)
(2)
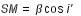 (3)
(3)
 En savoir plus
En savoir plus
Le tableau suivant donne les valeurs extrêmes des paramètres, l'étude des séries donnant l'orbite de la Lune, montre qu'au voisinage de la nouvelle Lune (et de la pleine Lune) la valeur de l'inclinaison est maximale, il convient donc de prendre i ~ 5° 17' dans ces formules.
Valeurs extrêmes et moyennes des paramétres
| Paramètres |
Maximum |
Minimum |
Moyenne |
| q |
16,2 |
10,9 |
13,5 |
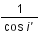
|
1,0052 |
1,0043 |
1,00472 |
Parallaxe de la Lune 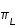
|
61' 27" |
53' 53" |
57' 2,70" |
Parallaxe du Soleil 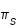
|
8,96" |
8,65" |
8,80" |
Demi-diamètres de la Lune 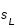 |
16' 45" |
14' 41" |
15' 32,58" |
Demi-diamètres du Soleil 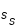
|
16' 18" |
15' 46" |
15' 59,63" |
Valeurs extrêmes et moyennes des paramètres.
 En savoir plus
En savoir plus
Le critère en latitude s'écrit donc :
si 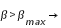 pas éclipse
pas éclipse
si 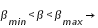 éclipse possible
éclipse possible
si 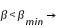 éclipse certaine
éclipse certaine
Si l'on utilise les paramètres du tableau précèdent on trouve 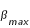 = 1° 34' 45,69" et
= 1° 34' 45,69" et 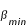 =1° 24' 37,31" et une valeur moyenne
=1° 24' 37,31" et une valeur moyenne 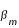 = 1° 28' 51" soit environ 1,48°.
= 1° 28' 51" soit environ 1,48°.
Le critère pour la centralité se calcule d'une manière analogue, il suffit de remplacer la somme des demi-diamètres apparents par la différence des demi-diamètres apparents dans l'équation (5). On obtient alors 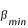 = 0° 52' 55,47" (soit environ 0,88°) et
= 0° 52' 55,47" (soit environ 0,88°) et 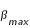 = 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne
= 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne 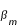 = 0° 56' 42,84" (environ 0,95°).
= 0° 56' 42,84" (environ 0,95°).
Le critère sur la latitude du centre de la Lune, peut se traduire en un critère sur la longitude de la conjonction Lune Soleil (donc la longitude) du Soleil par rapport au noeud de l'orbite lunaire. Ainsi il y aura éclipse si au moment de la conjonction en longitude, la différence de longitude entre le noeud de l'orbite lunaire et la longitude du Soleil est inférieure à 15,665°, il n'y aura pas d'éclipse si cette différence est supérieure à 17,375°, et il y aura peut-être éclipse si elle est comprise entre ces deux valeurs. Comme on le voit le critère en longitude est beaucoup plus large en amplitude que le critère en latitude, cela s'explique par la faible valeur de l'inclinaison de l'orbite lunaire.
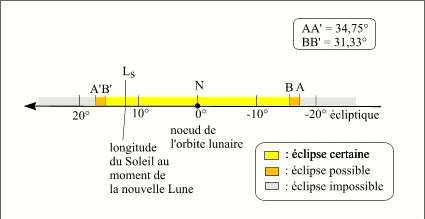
Critère en longitude pour les éclipses de Soleil (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
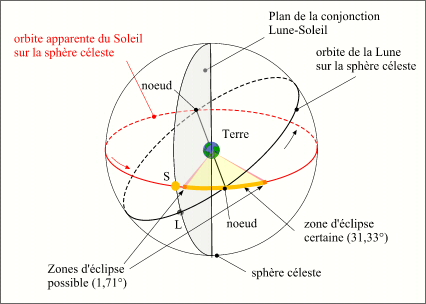
Critère en longitude pour les éclipses de Soleil (vu depuis l'espace)
Crédit : IMCCE/Patrick Rocher
 Introduction
Introduction



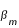 = 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à
= 1,48° et pour avoir des éclipses centrales il faut que b soit inférieure à  = 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).
= 0,95°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses partielles (36%) et la proportion d'éclipses centrales (64%).

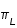 .
.
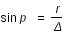 ,
, 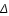 étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.
étant la distance entre le centre de la Terre et le centre du corps, et r le rayon terrestre. On constate que plus le corps est loin de la Terre plus le sinus est petit et plus la parallaxe est faible.

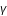 : l' angle S0M0S.
: l' angle S0M0S.
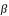 : la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
: la différence des latitudes entre la Lune et le Soleil à l'instant de la conjonction.
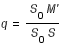 soit
soit 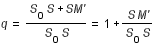
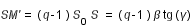 avec
avec 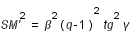
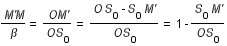
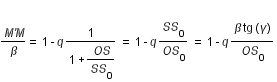
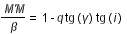
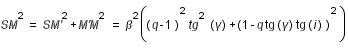 (1)
(1)
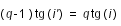
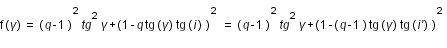
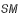 est minimum lorsque
est minimum lorsque 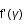 la dérivée de f est nulle
la dérivée de f est nulle
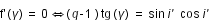 (2)
(2)
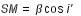 (3)
(3)
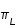 et
et 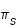 de la Lune et du Soleil.
de la Lune et du Soleil.
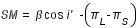 (4)
(4)
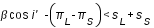
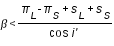 (5)
(5)
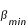 du second membre de (5) est obtenue avec
du second membre de (5) est obtenue avec 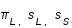 minimales et
minimales et 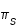 maximale, la valeur supérieure
maximale, la valeur supérieure 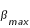 est obtenue avec
est obtenue avec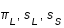 maximales et
maximales et 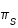 minimale.
minimale.
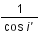
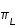
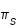
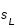
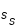
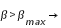 pas éclipse
pas éclipse
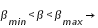 éclipse possible
éclipse possible
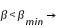 éclipse certaine
éclipse certaine
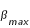 = 1° 34' 45,69" et
= 1° 34' 45,69" et 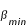 =1° 24' 37,31" et une valeur moyenne
=1° 24' 37,31" et une valeur moyenne 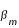 = 1° 28' 51" soit environ 1,48°.
= 1° 28' 51" soit environ 1,48°.
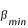 = 0° 52' 55,47" (soit environ 0,88°) et
= 0° 52' 55,47" (soit environ 0,88°) et 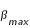 = 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne
= 1° 3' 14,98" (soit environ 1,05°) et la valeur moyenne 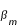 = 0° 56' 42,84" (environ 0,95°).
= 0° 56' 42,84" (environ 0,95°).

